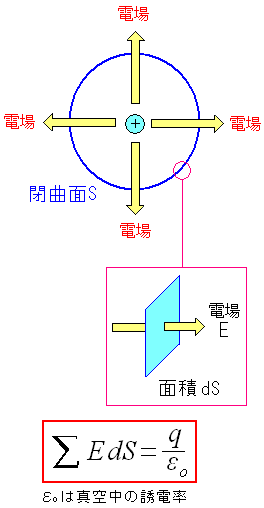
さて、ガウスの法則とは
荷電粒子と、それが作り出す電場の関係式なのだ。
求め方は、荷電粒子のある空間を覆う面があるとする。
面と垂直に貫く電場の積を足しあわせていくと
上図のような関係式になるのだ。
システム奮闘記:その105
(2016年5月22日に掲載)
電気力線
「システム奮闘記:その98」(電気回路入門)でコンデンサーの 説明をする際に、ガウスの法則がでてきた。 そこで復習をしてみる事にした。 ガウスの法則とは、荷電粒子と、それが生み出す電場の量の関係式だ。 荷電粒子を球体で囲んだ例を考える。
| ガウスの法則 |
|---|
 |
|
電場とは荷電粒子が作り出す空間の状態の事だ。 さて、ガウスの法則とは 荷電粒子と、それが作り出す電場の関係式なのだ。 求め方は、荷電粒子のある空間を覆う面があるとする。 面と垂直に貫く電場の積を足しあわせていくと 上図のような関係式になるのだ。 |
でも、なぜ、そんな式がでてきたのか。
調べてみる。
まずは、電場の様子を視覚的にするために
電気力線
がファラデーによって考え出された。
| 電気力線 |
|---|
 |
|
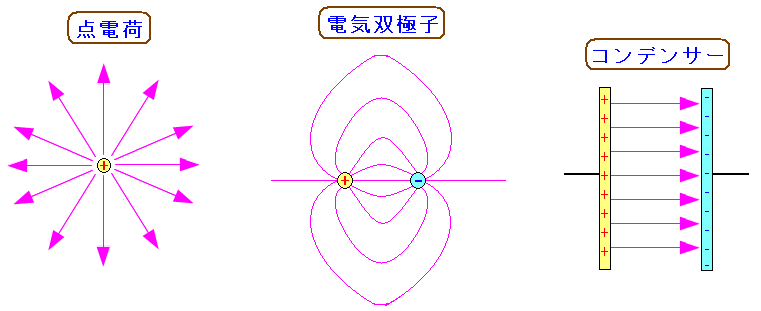
電場を視覚的に表わすためにできた仮想の線なのだ。 点電荷、電気双極子、コンデンサーの場合を描いてみた。 |
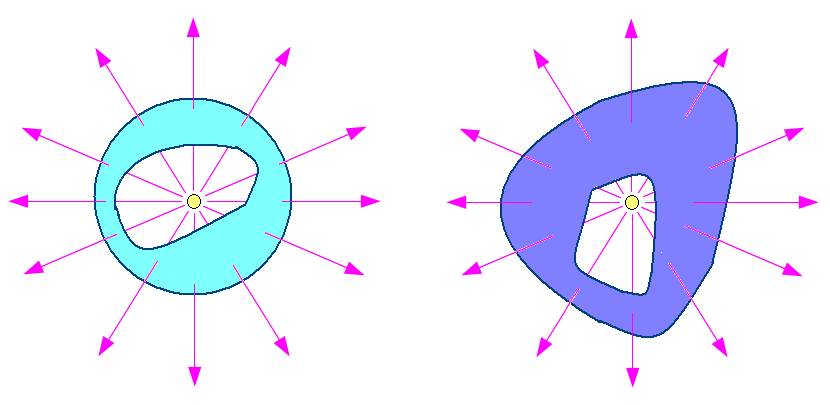
そして 電気力線の密度が高いほど 電場が強い のだ。 なので点電荷から放射状に伸びている電気力線は 遠くへ行けば行くほど、電気力線の密度が低くなるため 電場が弱くなるというのだ。 そして1835年、ガウスがガウスの法則を発見する。 電荷を覆う閉曲面を貫いて出ていく電気力線の本数は、 どんな曲面であっても同じになるというのだ。 図にすると以下のようになる。
| 曲面を貫いて出る電気力線の本数は同じ |
|---|
 |
|
電荷を覆う曲面の形が違っても、曲面を貫いて外に出て行く 電気力線の本数は同じ。 |
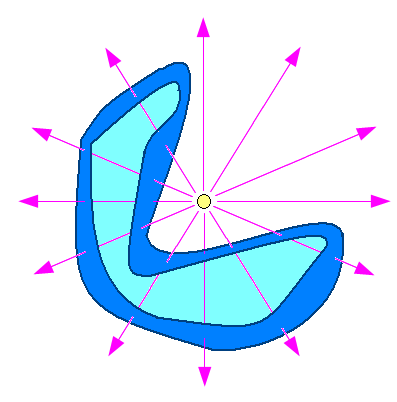
もし、曲面内に電荷がない場合はどうなのか。 ゼロになる。図にすると以下のようになるのだ。
| 内部に電荷がない閉曲面を貫く電気力線はゼロ |
|---|
 |
|
曲面に入る電気力線と出ていく電気力線の数は同じなので 合計するとゼロになるのだ。 |
1867年に数式化したものを発表したというのだ。 1835年に発見されて、発表するまでに32年。 なんで32年もかかるねん??? その上、1867年は・・・ 既にガウスはこの世を去っていた なのだ。 ガウスは1855年に亡くなっている。 なぜガウスが生きている間に、ガウスの法則が発表されなかった理由は 調べてみたが、わからなかった。 ガウスの法則を数式化すると以下のようになる。
| 閉曲面内部に電荷がない場合 |
|---|
 |
|
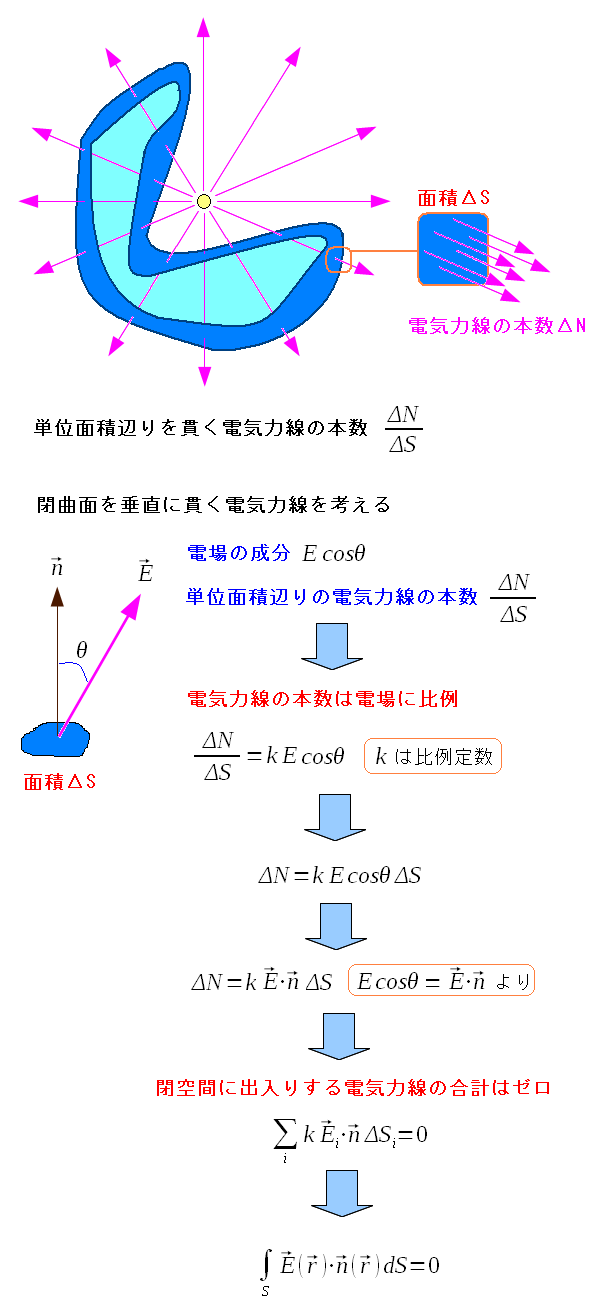
曲面に入る電気力線と出ていく電気力線の数は同じなので 合計するとゼロになるのだ。 それは曲面の形には関係ないのだ。 |
そして閉曲面内部に電荷がある場合。
| 閉曲面内部に電荷がある場合 |
|---|
 |
|
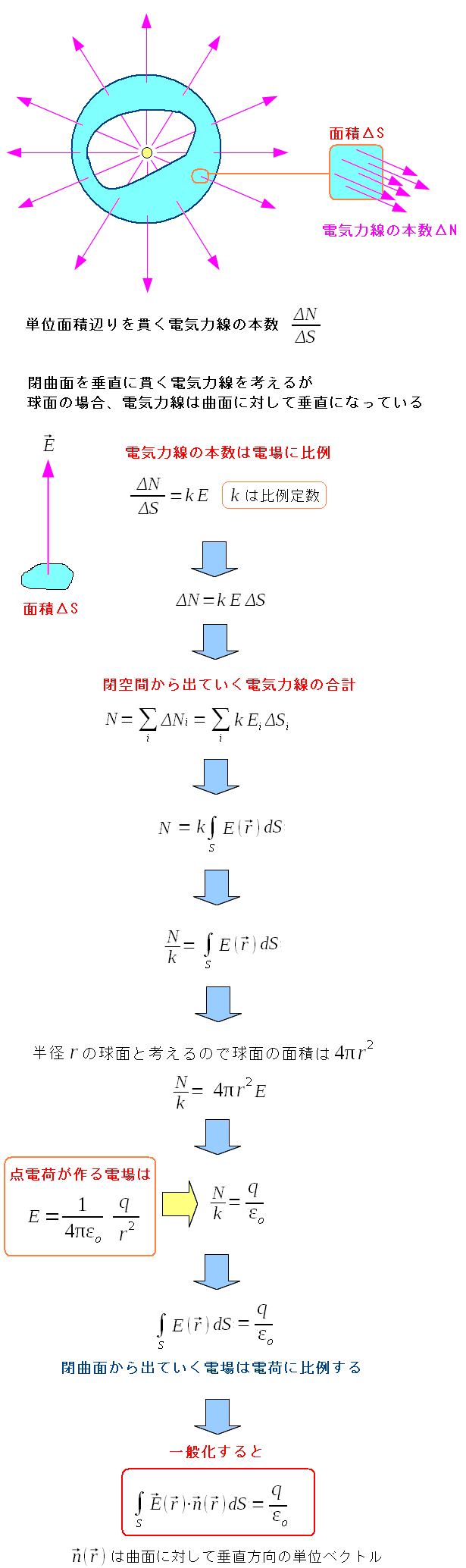
曲面の外へ出ていく電気力線は、電場に比例している。 単純に閉曲面を球面とした場合で求めてみた。 もちろん曲面が球面でなく、いかなる形でも 曲面を突き抜ける電気力線(電場)の合計は、電荷に比例するのだ。 |
閉曲面内部に電荷の有無の場合がある。 ガイスの法則の式を整理する。
| ガウスの法則の式 |
|---|
 |
ここで気づいた人がいるかもしれない。 もし、点電荷が作る電場と、それを球面で覆った場合 点電荷と電場と球の表面積と関係式(ガウスの法則)がどうなるのかだ。
| ガウスの法則:点電荷が作る電場と球面の関係式 |
|---|
 |
|
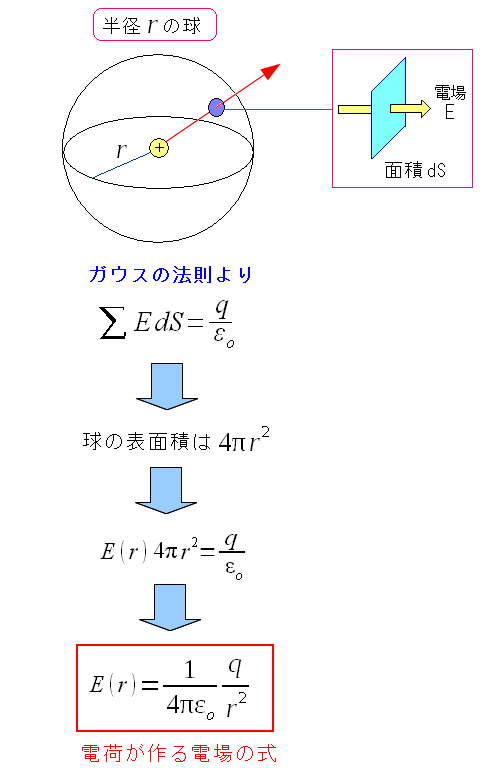
ガウスの法則に従って、点電荷の電荷量と rだけ離れた位置の球面の表面積と電場の積を計算すると 点電荷が作る電場の式になる。 点電荷が作る距離rでの電場の式で、4πr^2は r地点での球面の面積になるのだ。 |
電荷が作る電場で、比例定数部分の4πの意味は 球面の面積を求めるために、意図的につけたというわけではない。 もっと別の所に理由ある。それについては後述しています。 ガウスの法則がわかった。 ところで、ここまでで説明したのは ガウスの法則の積分形 なのだ。 通称「ガウスの法則」なので、積分形という言葉を抜かしても 支障はないのだ。
ガウスの法則の微分形
ガウスの法則の積分形があるという事は別の形がある事を意味する。 それはガウスの法則の微分形になる。 最初に式で表すと以下の形になる。
| ガウスの法則の微分形 |
|---|
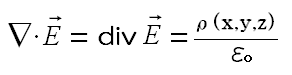 |
ところで微分形という言葉が出てきた。 電磁気の式では積分形(省略する事が多い)と微分形とわけている場合がある。 どういう違いなのか図で表現してみた。
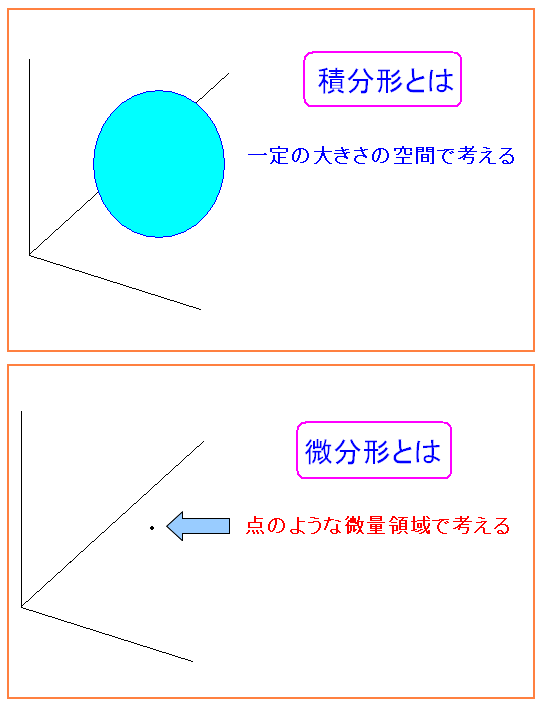
| 積分形と微分形の違い |
|---|
 |
|
積分形は一定の大きさの領域での法則。 微分形は、点のような微小領域での法則。 全体としての見るか、点で見るかの違いなのだ。 |
ガウスの法則の微分形と微分形がどういう物なのかを書いたが 具体的に、一体、どういう法則なのか。 本を見ながら追っていく事にした。
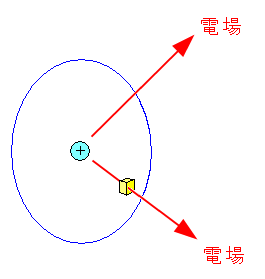
| 空間中の微小領域をを突き抜ける電場を考える |
|---|
 |
|
上図のように荷電粒子が作り出す電場が 空間中の極小領域を通過する場合を考がえる。 |
空間中の極小空間を拡大して考えてみる。
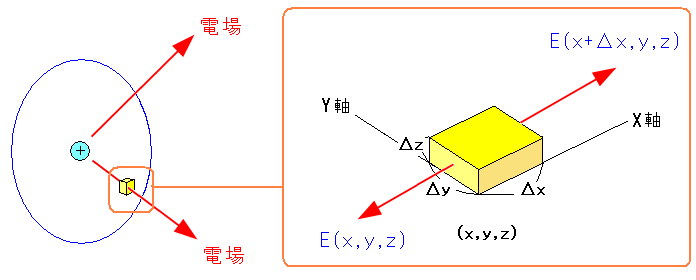
| 空間中の極小空間を拡大して考えてみる |
|---|
 |
|
微小領域(体積)を長方形と考えてみる。 電場が長方形を突き抜けた時の、電場の変化量を見てみる もし、その領域に荷電粒子がない場合は電場は変化しないが 荷電粒子が存在すると、電場は強さは変化する。 上図はX成分方向への変化量を描いていたのだ。 |
x成分方向での電場の変化量を計算してみる。
| x成分方向の電場の変化量を計算みる |
|---|
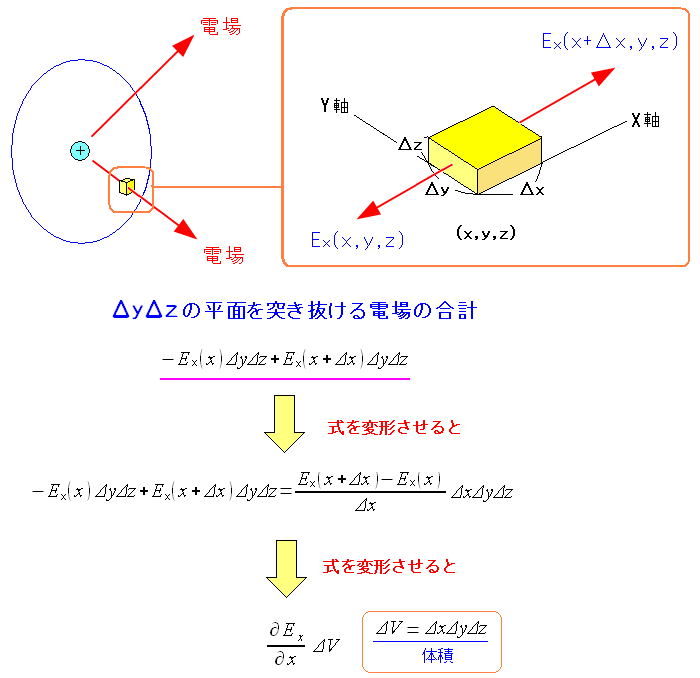 |
| x成分方向の電場の変化量の式が出てきた。 |
同様に、y成分、z成分の変化量も計算してみる
| x成分だけでなく、y成分とz成分も計算してみる |
|---|
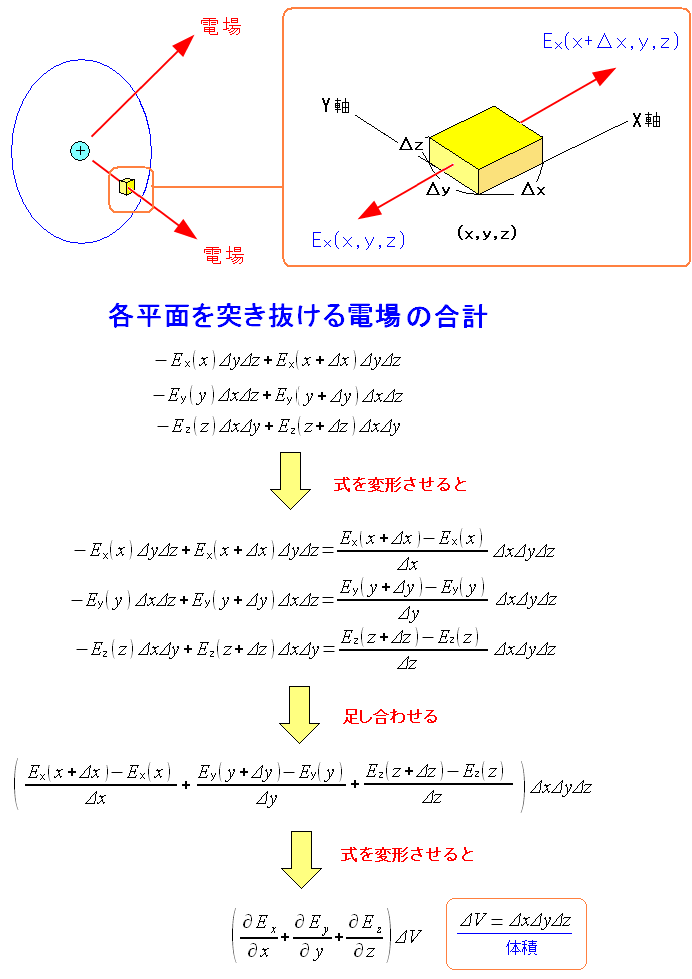 |
| 極小領域を突き抜ける電場の変化量を算出できる。 |
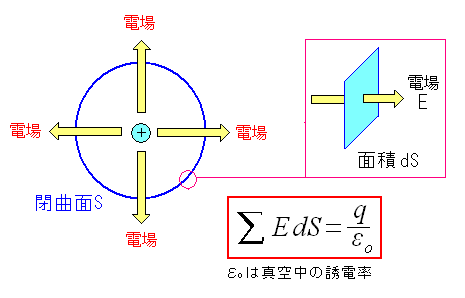
ここでガウスの法則を見てみる。
| ガウスの法則(積分形) |
|---|
 |
|
閉空間に荷電粒子がある場合、荷電粒子の電荷量と それを取り囲む閉曲面を貫く電場の量は、上の関係式になる。 |
まずは電場が突き抜ける領域に荷電粒子がない場合を見てみる。
| 電場が突き抜ける領域に荷電粒子がない場合 |
|---|
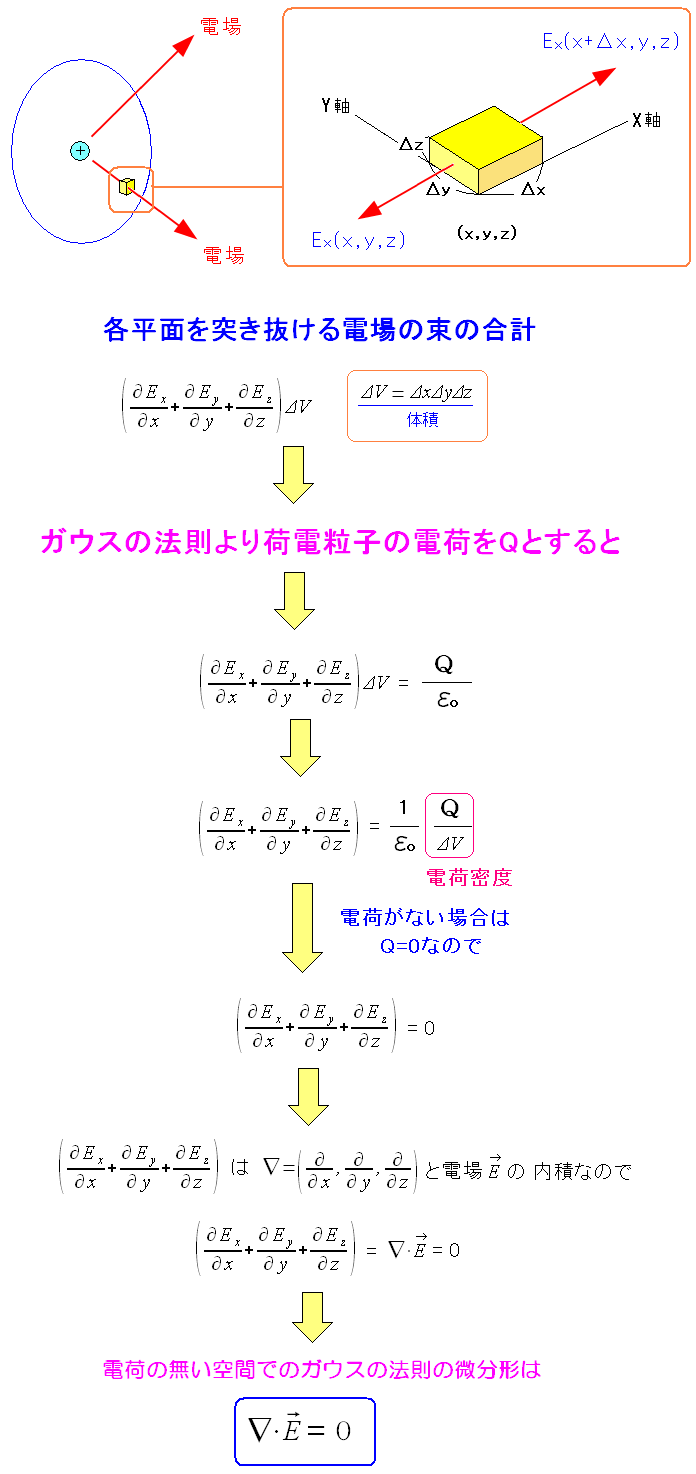 |
| 微小領域に荷電粒子がない場合の関係式が求まった。 |
もし、電場が突き抜ける領域に荷電粒子がある場合を見てみる。
| 電場が突き抜ける領域に荷電粒子がある場合 |
|---|
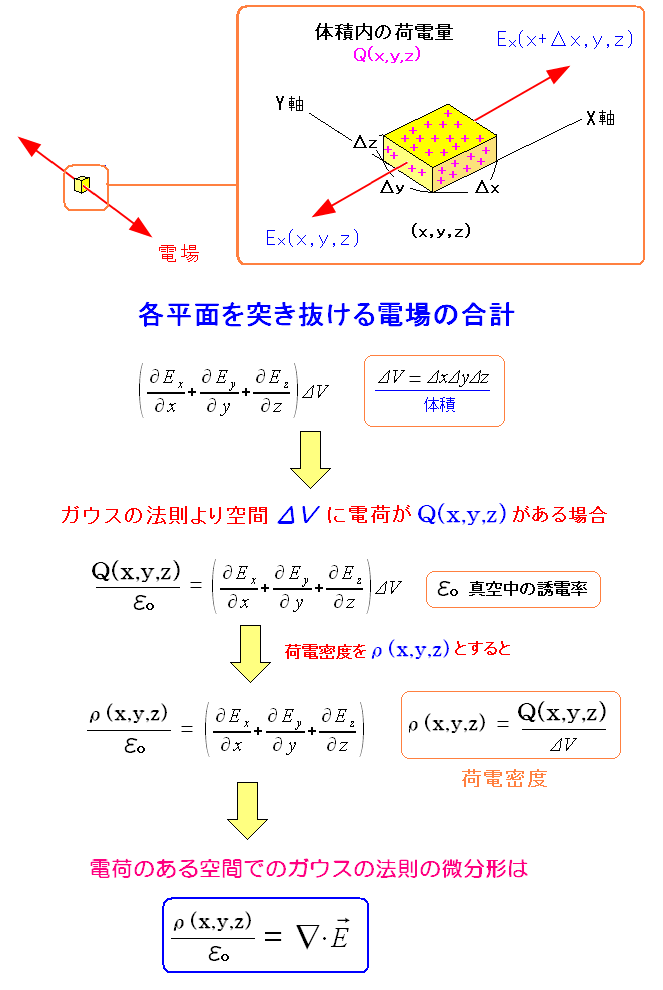 |
| 電場と、その領域の荷電密度の関係式が出てきた。 |
点の領域(微小空間)の部分の、荷電粒子と電場の関係式なので
ガウスの法則の微分形
と呼ばれるのだ。
| divは湧き出し |
|---|
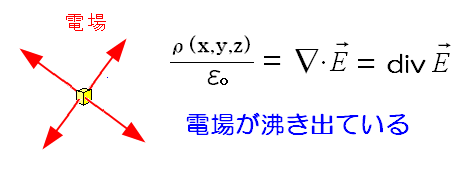 |
|
微小空間から電場が湧いてくるような感じなので divの意味を「湧き出し」と言うのだ。 |
ガウスの定理
ところで、ガウスの法則の積分系と微分形を結びつける式がある。 ガウスの定理 なのだ
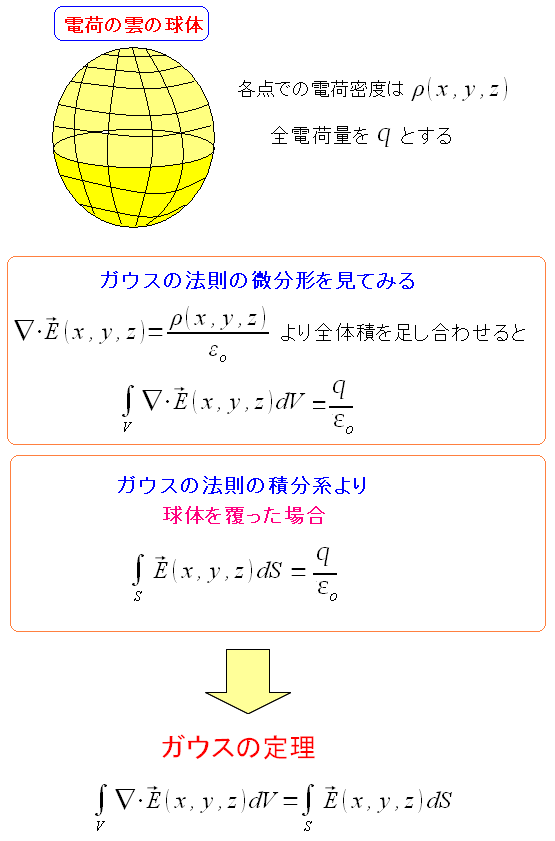
| ガウスの定理 |
|---|
 |
|
ガウスの法則の微分形は微小体積の電荷密度を表わす。 そのためガウスの法則の微分形で、全体積を足し合わせると 合計の電荷が求められる。 するとガウスの法則の積分形の式と一致するのだ。 |
ガウスの法則の微分形は、電場と微分演算子の内積
さて、ガウスの法則の微分形を見ていると、学生時代の時には気づかなかったが、 ガウスの法則の微分形の式の形が、電場と微分演算子との内積になっている。
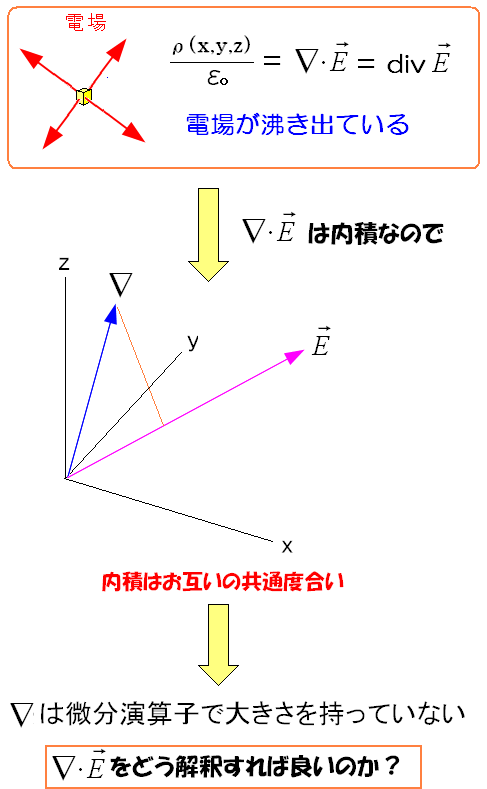
| ガウスの法則の微分形は、電場と微分演算子との内積 |
|---|
 |
|
ガウスの微分系は、微分演算子の▽(ナブラ)と電場の内積になっている。 内積とは類似性の指標になる。 「システム奮闘記:その104」(無線LAN入門 無線LANの基礎)で 相関関数の話で触れています。 |
そして思った。
▽(ナブラ)とは、どんなベクトルやねん!
| ▽(ナブラ)とは、どんなベクトル? |
|---|
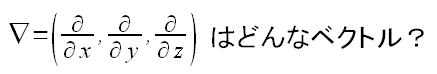 |
|
∇(ナブラ)をベクトルとして扱うと、ガウスの法則の微分形は ナブラと電場との内積という表記ができるので、綺麗な形になる 一見すると、▽(ナブラ)は演算子に過ぎないが あとで出てくる多様体の話になると、ベクトルの顔も持っている。 ただ、∇(ナブラ)は、どんな大きさで、どんな方向を持っているのかを 問うのは意味はない。 だが、この時はベクトルと思い込んだため、どういうベクトルなのか 色々考えたのだが、わからず、悩んでしまった。 詳しい事は後にある微分形式で書いています。 |
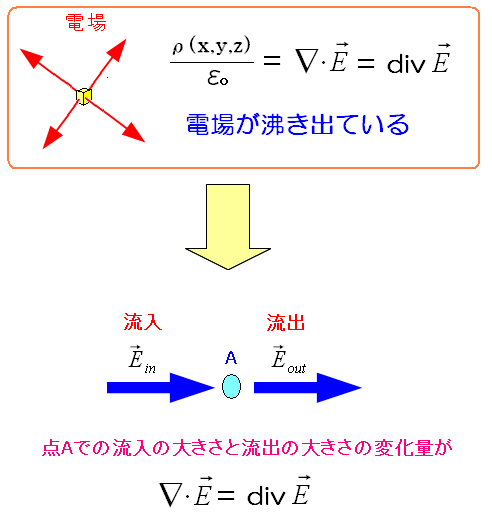
私が理系だったのは20世紀までの話。 21世紀の今は・・・ 数学はわからへん!! で逃げたい所。 だが、往生際の悪さは天才的な私。 蛇のように、しつこく調べていくと、外積代数と微分形式の分野に たどり着く。そして得た答えは・・・ ▽・Eは、電場のベクトル(E)の微分 なのだ。 さて、▽・Eは、電場ベクトル(E)の微分と考える。 ベクトルEの長さと方向は一定なので 変化量はゼロだから、▽・E=0になる というわけなのだ。 そして電場ベクトル(E)を「流れ」と考えると、変化量がゼロなのは 流入と流出が同じ というのだ。
| 入ってくるベクトルと出ていくベクトルの変化量 |
|---|
 |
|
流入と流出の変化量になるのだ。 電荷密度がある領域だと、流出が多くなるため divの事を「湧き出し」と言うのだ。 |
∇とベクトルの内積(div)が、ベクトルの微分である事を知るには 外積代数と微分形式の知識が必要になる。 物理法則の裏に隠れている数学を知る必要があるのだ。
| 本当の事を書くと |
|---|
|
「数学は、わからへん」で逃げる予定だった。 逃げていれば、2015年8月辺りに、この章の話が完成する予定だった。 だが、往生際の悪さが仇(?)になり、数学の壁に直面。 学生時代、全く習った事のない数学だけに、七転八倒の繰り返し。 でも、そのお蔭で、∇・EがベクトルEの微分だと知った上 電磁気の事で、更に知らない事がどんどん出てきた。 泥沼にハマらないようにするため、撤退(?)する勇気も必要だ。 |
電磁気学入門の目次
| 電磁気学入門:目次 | |
|---|---|
| スカラーとベクトル | 簡単なスカラーとベクトルの話です。 ベクトルは方向と大きさを持つ量。方向という量持っているだけに注意が必要です。 |
| 静電気の発見からクーロンの法則 | 今でこそ当たり前の静電気や導体、絶縁体、電荷など どういう経緯で発見し、クーロンの法則まで至ったのかの話です。 |
| クーロン力、電場、近接作用 | 4つの力のうち、クーロン力の位置づけ 電荷が作り出す作用の電場。近接作用の話です。 |
| 微分、全微分、方向微分 | 簡単な微分、全微分、方向微分の話です。 ここをしっかり押さえないと、電磁気の数式の意味が わからなくなります。 |
| ベクトル解析 |
電磁気に必要なベクトル解析の話です。 勾配(grad)、2次元のグリーン定理 ストークスの定理の話です。 |
| 電位ポテンシャル | 電位ポテンシャルです。勾配と電場の関係を使って説明しています。 |
| 電気双極子 |
電気双極子の話です。 物質中で起こる分極を理解するのに必要です。 |
| ガウスの法則 | ガウスの法則の積分形、微分形の話です。 |
| ポアソンの方程式、ラプラス方程式 |
ポアソンの方程式、ラプラス方程式の話です。 単に電荷分布から電位を求めるだけの話にとどまらない 奥が深い分野です。ポテンシャル論、デルタ関数 グリーン関数、固有値問題について触れています。 |
| 静電場と渦なしの法則 |
静電場で、電荷を1周させた時の仕事はゼロ 微分形と微分形の渦なしの法則の話です。 |
| ビオサバールの法則 |
電気と磁場の関係の発見の話から ビオ・サバールの法則が導かれるまでの話です。 |
| 磁気双極子 |
磁気双極子の話で、回転電流になります。 物質中の磁場の話にも関連します。 |
| アンペールの法則 |
アンペールの法則の話です。 積分形・微分形だけでなく、閉回路に流れる電流が作る 磁気双極子の話なども書いています。 |
| ローレンツ力 |
磁場中を移動する電荷にかかる力(ローレンツ力)の話です。 ローレンツ力は相対性理論が絡んでいる事も紹介しています。 |
| ファラデーの誘導起電力の法則 | ファラデーの誘導起電力の話です。 |
| うず電流を使った簡単な物理実験 | 電力計に使われるアラゴの円盤。 そしてIH調理器で熱するために発生させる、うず電流は レンツの法則から電流が発生する原理を応用した物だ。 アラゴの円盤の実験と、IH調理器を使った実験です。 気分転換で読んでください。 |
| ベクトルポテンシャル |
わかりにくいベクトルポテンシャルの話です。 電位は電荷が作る電気のポテンシャルだが ベクトルポテンシャルは電流が作る磁場のポテンシャルの話です。 |
| オームの法則の微分形 | 微小領域でのオームの法則の話です。 |
| マックスウェルの方程式 |
4つのマックスウェルの方程式を書いています。 電場と磁場の変化を図にする事で rotの回転の意味も理解できます。 |
| ゲージ変換 |
ゲージ(gauge)は物差しの意味です。 マックスウェルの方程式をE(電場)とB(磁場)の関係式から φ(電位ポテンシャル)とA(ベクトルポテンシャル)の関係式に 書き換える際、ゲージ変換が使われます。 ゲージ変換の役目を書きました。 |
| 電磁波 |
マックスウェルの方程式から電波が伝わる様子を 視覚的に見てみる話です。 |
| 回転のrotはベクトルの微分 |
ベクトル解析や渦なしの法則で出てくるrotは ベクトルの微分という話です。 |
| 電磁気学の単位系 | 電磁気学の単位系の話です。 物理量の単位系の指数を見る次元解析 電磁気学の歴史と単位系の変遷について触れました。 |
| 電気泥棒:電気と法律の話 |
電気は物体なのか、無形物なのか。 明治時代に、電気を無断で使った場合、物か、そうでないかで 窃盗罪になるかどうかが裁判で問われました。 ちょっとした科学と法律の話です。気分転換で読んでください。 |
| 数ベクトルと基底ベクトル | ベクトルの話です。 矢印だけがベクトルでない事。 数ベクトルと基底ベクトルの違いの話です。 多様体、反変・共変ベクトルを理解するのに必要です |
| 多様体 | 空間を一般化した話です。 ▽(ナブラ)の正体に迫まります |
| 外積代数 |
外積、テンソルについて書いています。 極性ベクトル、軸性ベクトル 外積は行列で、ベクトルは見せかけの姿だった話です。 |
| ベクトルの双対関係 |
反変ベクトル、共変ベクトル、双対関係 ベクトル解析、外積代数の話 外積、テンソルについて書いています。 |
| ローレンツ力と相対性理論 |
磁場は電場の相対論的効果だった話です。 ローレンツ力を使って、導線が作る磁場を使って説明です。 |
| 微分形式 |
多様体の話の続きです。 座標に依存しない形での関数やベクトルの微分の話です。 ガウスの法則、アンペールの法則、マックスウェルの方程式が 鮮やかな形で表現できます。 ∇(ナブラ)の正体もわかります。 |
| 物理と対称性 |
マックスウェルの方程式をよく見ると対称性があります。 物理の方程式と対称性を数学的な観点でみると 意外なつながりがあるという話です。 |
| マックスウェルの応力 |
電気力線を弾性体(ゴム)とみなして、力の伝わり方などを 説明した考え方です。 |
| 電場エネルギー | 電場が持つエネルギーの式を導いた話です。 |
| 磁場エネルギー |
磁場が持つエネルギーの式です。 手抜きの説明と、直流RL回路を使った説明を書きました。 |
| ポインティングベクトル |
電磁エネルギーの流れ「ポインティングベクトル」の話です。 電磁波でもエネルギー保存則が成り立つ話から ポインティングベクトルを導いています。 |
| 電気エネルギーは導線の外を伝わる |
導線の外を電気エネルギーが流れる話です。 私が誤解した事、その誤解を解いていく過程を紹介しながら 「目からウロコ」にたどり着いた話です。 |
| 物質中の電場 | 物質中の電場の話です。 分極の話をしながら、物質中の電場の話をします |
| 物質中の磁場 | 磁性の話をしながら、物質中の磁場の話をします |
| 物質中のマックスウェルの方程式 | 物質中でもマックスウェルの方程式が成り立つ話です。 |
| 導体に侵入する電磁波 |
導体に侵入する電磁波が減衰していく話です。 表皮効果と同じ「表皮の厚さ」が出てきます |
| 表皮効果 |
目的の表皮効果の話です。 マックスウェルの方程式を解きながら 交流電流の周波数を上げると、表面にしか電流が流れなくなる話です。 |