システム奮闘記:その104
(2014年8月16日に掲載)
無線LAN導入の経緯 社内で無線LANの導入は、少し出たりしたりしたが 電波漏洩の問題があり、見送られてきた。 実際、10年前に無線LAN機能付のノートパソコンを持ち込んだ同僚が 無線LANを拾える と言った。 近所の会社や住宅から出ている無線を捕まえたためだった。 そのため・・・ 無線はセキュリティー上、問題がある で、無線LANの導入は行なわれなかった。 実際、社内用のため、LANケーブルを使えば良いだけで わざわざ無線LANを導入する必要はなかった。 そして、私自身、無線まで手が回らないためIT担当者なのだが 必然的に・・・ 抵抗勢力 になっていたのだ。 だが、2014年、ある営業所が移転する事になり 移転先にできる会議室で 無線LAN導入 が決まった。 お客さんを集めて研修する場で、いつでもLANが使えるようにするためだ。 そうなると抵抗勢力でいつづけることができなくなる私。 そこで無線LANの勉強を始める事にした。 量が膨大になったので、目次を作成しました。
| めちゃくちゃ大雑把な目次 | |
|---|---|
| (1) | 信号変調の概略 |
| (2) | 直接拡散方式変調(DSSS) |
| (3) | ODFM変調の仕組み |
| (4) | 誤り率の算出法 |
| (5) | ローパスフィルター |
| (6) | 導入実験 |
外注する場合でも無線LANの知識は必要
無線LANの装置の選定や設置を外注すれば良いと思われがちだが 大きな問題があった。 業者の提案した装置の良し悪しが判定できへん なのだ。 そして業者に丸投げしても、トラブルが起これば 私が障害対応しなければならない というわけで、それだったら、事前に調べられる事は調べて 機種選定だけでなく、障害対応ができるようにしておいた方が良いと考えた。 色々、検索サイトで見てみる。 これだけはやっておきたい!「無線LAN情報セキュリティ3つの約束」:政府広報オンライン 「“ただ乗り”を するなさせるな 無線LAN」IPAがセキュリティ設定を呼び掛け -INTERNET Watch 家庭用無線LANを使う上での注意点だ。 確かに電波なので、外部から電波を拾って、ただ乗りする人もいれば 踏台にする輩もいる。 そして外出先で無線LANを使う事で、パソコンのデータ漏洩の問題などが出てくる。 こんな物を見ていると、例え無線LANがボタン1つで動かす事ができても 注意深く運用する必要がある になる。
無線LANの規格
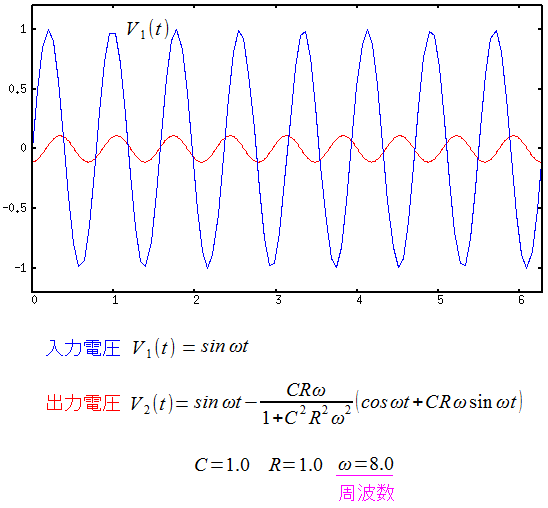
無線LANだが、良い本があった。 「最新LANハンドブック」(宮越 健、角田浩二:秀和システム) 無線LANだけでなく、LAN全般の事が書いている、分厚い本だ。 10年前にLANの勉強する際に購入した本だ。 ただ、現在では絶版になっている。周波数帯
無線なので電波を飛ばして通信を行なう。 使っている周波数は、2種類ある事を知る。 2.4GHz帯域と5.2GHz帯域 だ。 元々は2.4GHz帯域だったが、2.4GHz帯域はISM帯域のため 電子レンジやbluetoothとかち合う問題 が起こるため、5.2GHz帯域が割り当てられたという。 ところで・・・ ISM帯域って何やねん? なのだ。 知ったかぷりしてもメッキが剥がれるだけなので、ここは素直に わからんと書いて、ISM帯域が何かを調べてみる。
| ISM帯域とは |
|---|
|
ISMは「Industrial Scientific and Medical」の略だ。 産業・科学・医療用に割り当てられた電波帯域で 電子レンジやbluetoothに使われている。 |
ところで「bluetooth」という文字はよく見るのだが
それが何なのか聞かれると
bluetoothって何やねん?
なのだ。
それも調べてみた。
| bluetoothとは |
|---|
|
近距離用の無線通信の規格だ1998年にできたという。 ワイヤーレスマイクや、リモコンなど 本当に近距離での通信に使われているのだ。 |
ネット検索すると、IO-DATAのサイトを発見。 無線LAN規格の違い|無線LAN | IODATA アイ・オー・データ機器 無線LANには以下の規格がある。
| 無線LANの規格と周波数帯 | |
|---|---|
| 11n | 2.4GHzと5.2GHz |
| 11a | 5.2GHz |
| 11g | 2.4GHz |
| 11b | 2.4GHz |
|
(注意) 2013年より11acも加わっていますが、調べた時点では 4種類しかなかったので、勉強過程を忠実に書くために ここでは4種類と書きました。 | |
自宅に無線LANを導入している同僚と話をした。
| 同僚との会話 | |
|---|---|
| 私 | Zさん(仮名)の家に無線LANがありますけど 電子レンジで通信が悪くなる事、ありますか? |
| 同僚 | それはあるなぁ。 インターネット使っている時は 電子レンジを使うのは、やめてくれと言ってるよ |
電子レンジは2.4GHz帯で無線LANの帯域と同じなので 通信障害になるようだ。 うちの会社で扱っている機械で電波を飛ばす物がある。 Bluetooth というロゴが張っている。 お客さんを呼んで機械のデモを行なう事がありえるため その機械を使っている最中でも無線LANが使えるかどうか 確認が必要になってくる。IEEE802.11
IEEE802.11とは無線LANの標準規格だ。 IEEE802.11とは(IT用語辞典) ところで無線LANの事を WLAN (Wireless LAN) と呼ぶ。 知らなかった。無線LANのネットワーク形態
本を読み進めると、無線LANのネットワーク形態の説明があった。BSS (Basic Service Set)
本にはステーション(STA)同士の通信と書いていた。 ステーションって何やねん? カタカナを使われると、意味不明になる。 ステーションとは駅の「Station」と同じ単語だ。 そこで英和辞典を見てみる事にした。
| 「Station」の意味 |
|---|
|
「駅」の意味だけでなく、「放送局」や「位置」や 「立場」や「身分」などの意味がある。 |
駅以外の意味があったとは知らへんかった
パソコンが通信の際、無線局として電波を発信する事から
放送局の意味のステーションという言葉が名付けられているようだ。
本の説明を図式化すると以下の通りになる。
| BSSとは(1) |
|---|
 |
| パソコンやデジタル機器同士がお互い通信しあう領域だ。 |
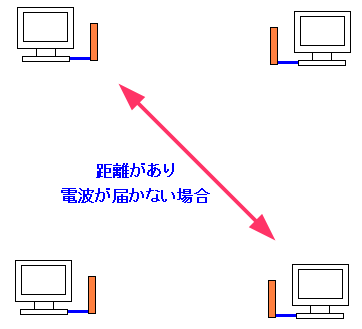
だが、パソコンやデジタル機器だけの集まりだと以下の問題がある。
| お互いが通信できない距離にある場合 |
|---|
 |
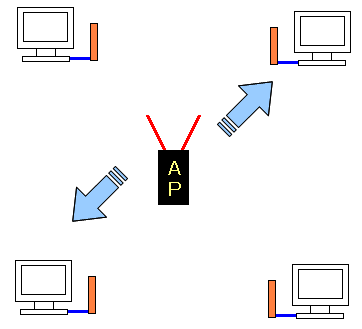
本には、もう1つのBSSの説明があった。 そして以下のサイトでも、同じ事が説明している。 無線LAN - BSSIDとESSID
| BSSとは(2) 無線アクセスポイント(AP)を置いた通信できる領域 |
|---|
 |
|
パソコン、デジタル機器が通信可能な所に無線アクセスポイント(AP)を設置。 無線アクセスポイント(AP)の傘下に入っているパソコンやデジタル機器の集まり (ステーション群)の事を「BSS」というのだ |
つまり・・・ 1つの無線アクセスポイントの傘下にあるパソコンやデジタル機器群 がBSSの意味になるのだ。ESS
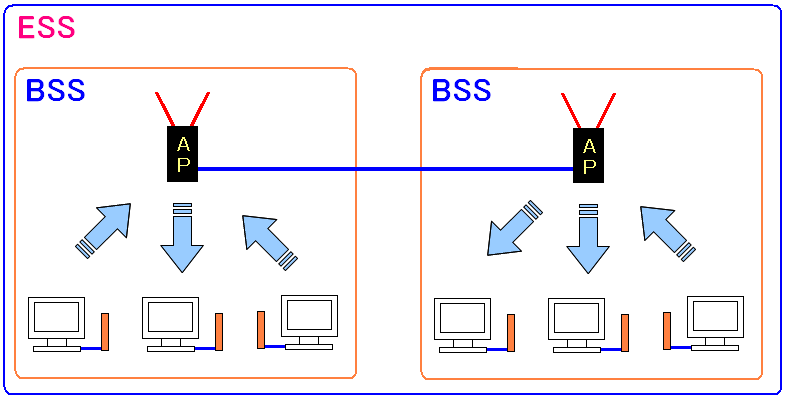
ESSとは・・・ Extended Service Set の略なのだ。
| ESSとは |
|---|
 |
|
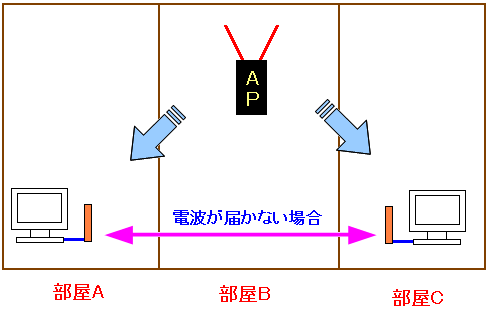
いくつかのBSSを束ねたネットワーク形態の事をいう 例えば、事務所などで部屋や階が違うと電波が届かない場合がある。 そこで部屋ごとに無線アクセスポイントを置き、上図のようにする事がある。 このような形態をESSと呼ぶのだ。 |
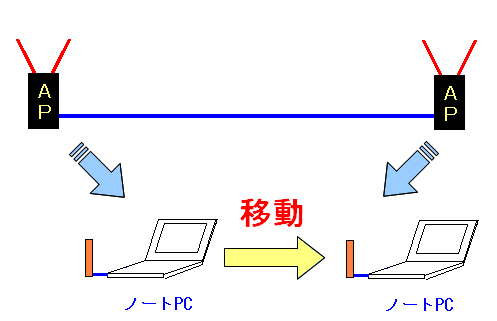
ローミング
携帯電話でも「ローミング」というのがあった。 英単語の綴りだと「Roaming」になる。
| ローミング(Roaming)とは |
|---|
 |
|
「Roam」とは、「散策・放浪・自由に歩き回る事」の意味がある。 「Roaming」は、「自由にさまよっている事」の意味になる。 無線LANや携帯電話のローミングとは、複数の無線アクセスポイントの傘下を 自由に移動し通信できる事を指す。 |
CSMA/CA
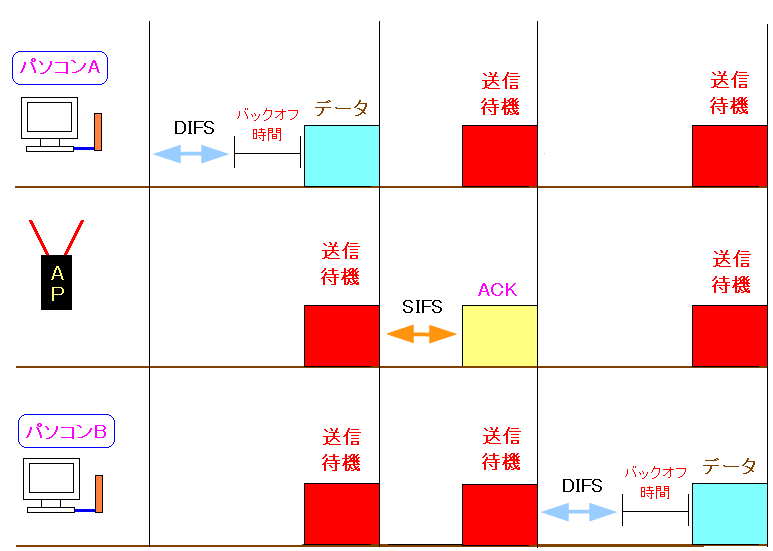
無線LANの通信方法にCDMA/CAというのがあるのだが CSMA/CAって何やねん! なので、意味を調べてみた。 Carrier Sense Multiple Access with Collision Avoidance だという。 日本語訳は「搬送波感知多重アクセス/衝突回避方式」だという。 いまいち、わからん。要するに、全くわからん。
| CDMA/CAを使った通信方法 |
|---|
 |
|
パソコンは、データ送信をする前に、DIFSという時間おく。 そして各ステーションが持っているバックオフ時間以内に 通信が行なわれていないと、パケットの衝突が起こらないとみなして パソコンがデータ送信を行なう。 その間、他のステーションは送信待機状態になる。 そしてデータ送信後、データを受け取ったアクセスポイントが SIFS時間の後、パケットの衝突が起こらないとみなして ACK信号(送信完了)を送る。 全ステーションがACKを受け取るため、送信待機状態になる。 |
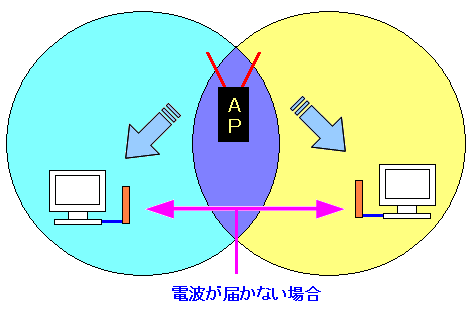
だが、これは、アクセスポイントの傘下にあるパソコン同士が お互いの存在がわかっているため、パソコンAがデータ送信を開始すると パソコンBがデータ送信しているのを感知して、待機状態になる。
| こんな状態の場合は |
|---|
 |
|
アクセスポイントの傘下にあるパソコン同士で、距離があるため お互いの電波が届かず、お互いの存在が見えない場合がある。 |
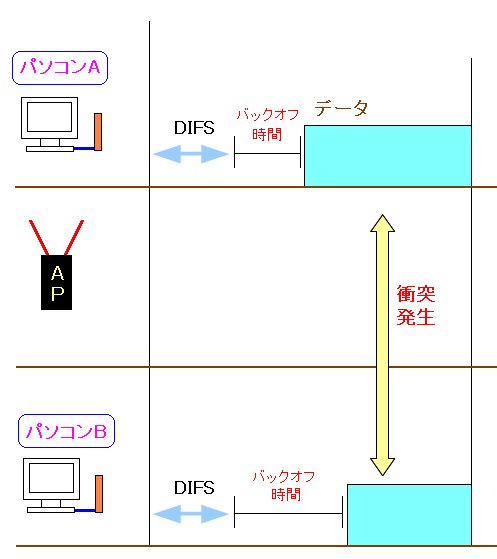
上図の場合、パソコンAがデータ送信を開始しても、パソコンBは、 それが感知できないため、パソコンBもデータ送信を開始して パケットの衝突が発生してしまう。
| お互いが見えていないと衝突が起こる |
|---|
 |
|
パソコンAとパソコンBがお互い、見えていない状態だったとする。 この場合、パソコンAがデータ送信を行なっても パソコンBは感知できないため、パソコンBもデータ送信してしまい 結果、パケットの衝突が発生してしまうのだ。 |
調べてみると、パケットの衝突対応に方法が 有線と無線とは異なる手法を使っているという。 有線LANの場合、CDMA/CDが使われている。 詳しくは「システム奮闘記:その24」(LANの設定・仕組み)を、ご覧ください。 CDMA/CDの「CD」の意味は衝突検出だ。 有線の場合、「衝突検出」という手法を採用している。 衝突を検知できるからだ。 だが、無線の場合、パケットの衝突を検知できない。 そこで「衝突回避」という手法を取る。隠れ端末問題
無線LANの場合アクセスポイントの傘下に複数台の ステーション(パソコンや携帯端末)などが、ぶら下がっている。 有線LANの場合、LANケーブルで結ばれているため、お互いが見えている。 だが、無線の場合、以下の問題が起こる。
| 隠れ端末問題 |
|---|
 |
|
隠れ端末問題とは、無線アクセスポイントにぶらさがっている パソコン同士が、お互い見えていない状態だ。 そのため双方が同時にデータを送信すると衝突してしまうが お互いが見えていないため、衝突に気づかないという問題がある。 |
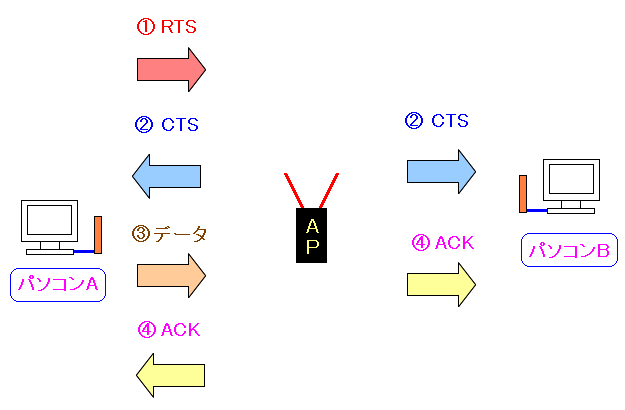
CDMA/CA方式では衝突防止ができなくなる。 そこで以下のような対応策を取るという。 CSMA/CA with RTS/CTS TCP/IP入門
| 隠れ端末問題対策 |
|---|
 |
|
パソコンAが無線を使いたい場合、RTS(Request To Send:送信要求)を送る。 パソコンAからRTSを受け取った無線LANアクセスポイントは 全てのパソコンに対してCTS(Clear To Send:送信準備完了)を送る。 この時、パソコンAに送信する事を知らせるのだ。 パソコンAはデータを送信する。 データ送信が終わると、アクセスポイントは、全てのパソコンに対して ACKを送る |
ところで英語の「clear」の意味は「消去」とか 「済みきった」の意味だと思っていたが、それだけではないようだ。
| 英語の「clear」について |
|---|
|
動詞の意味で「(審査)を通過する」の意味や、許可の意味がある。 CTS(Clear To Send)に「受信可能」と訳しているサイトがあるが 「Clear」の意味に許可の意味合いがあると、納得できる。 |
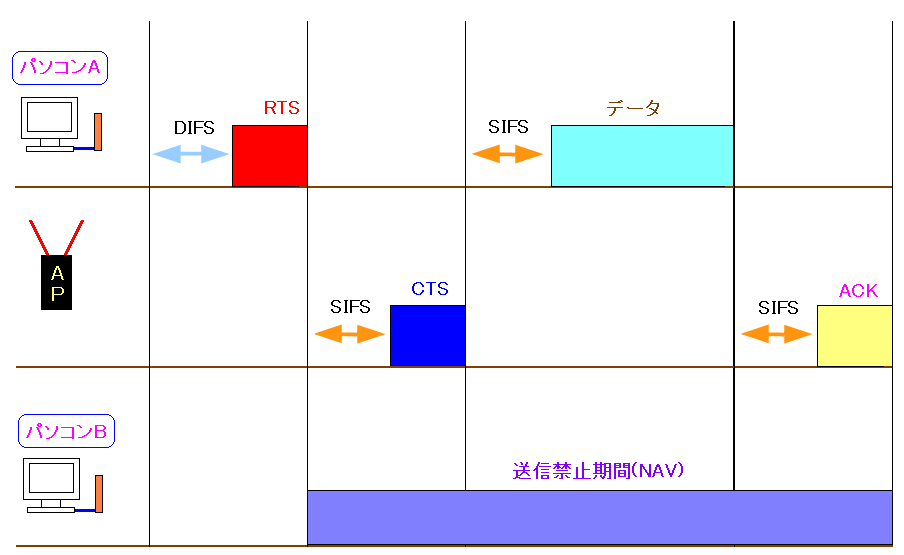
隠れ端末問題の対策。 パソコンとアクセスポイントの間でのやりとりの概略は、わかった。 だが、もう少し調べてみると、細かい話が出てくる。 ASCII.jp:有線とは違う、無線独自のアクセス技術とは? (1/2)|無線LANのすべて 無線LANでデータを送受信する仕組みをやさしく説く(4)――データのアクセス制御 無線LANテック - 解説記事/コラム-隠れ端末問題の解決 無線LANテック - 解説記事/コラム-DIFSとSIFSを使ったアクセス制御 無線LAN - CSMA/CAとは パソコンとアクセスポイントのやりとりを時系列に並べると 以下のようになる。
| パソコンとアクセスポイントのやりとり |
|---|
 |
|
DIFSは「DCF IFS」の略で、SIFSとは「Short IFS」の略だ。 パソコンが接続要求の「RTS」を送信する前にDIFSの時間を作っている。 |
ところで IFSって何やねん? なのだ。 そこで調べてみると・・・ Inter Frame Space (フレーム間隔) だという。 いまいち、よくわからん。 つまり全くわからん事を意味する。 DIFSはDCF IFSの略だ。 DFCは「Distributed Coordination Function」なのだが・・・ Distributed Coordination Function って何やねん なのだ。 日本語訳は「自律分散制御」なのだが・・・ 自律分散制御って何やねん! なのだ。 なんだか、ドツボにハマってきた感じだ。 だんだん、混乱してきた ここで、さっさと逃げる事を考えた。 ところで隠れ端末問題なのだが、隠れ端末がなければ 別にRTC/CTSをする必要はないはず。 そう思った人はいると思う。 RTS/CTSを使う問題点は、パケットのやりとりが増え、 通信速度が低下する事だ。 そのためアクセスポインタの設定で、RTS/CTSの利用をしない設定ができる。 それについては、後述しています。
| 事前に白状すると |
|---|
|
隠れ端末問題の話を見た時、全ての無線LAN通信で RTS/CTSが使われていると思い込んだ上 「隠れ端末が存在しない場合は不要」という発想は出てこなかった。 思考停止になっていた自分に対して反省なのだ。 |
信号変調
無線LANは、文字通り、電波を使って通信を行なう。 電波にする際、デジタル信号を変換しなければならない。 信号の変換処理の事を・・・ 信号変調 という。スペクトラム拡散
ISM帯域(2.4GHz)の無線LANの場合、限られた帯域を 効率良く使うため、スペクトラム拡散方式を使って データを送信しているという。 スペクトラム拡散って何やねん? よくわからん。 でも信号の周波数の帯域幅が広がるような感じに思える。 詳しい事は後述しています。 ところでスペクトラム拡散について、 本では2つの利点のある変調だと書いていた。
| スペクトラム拡散方式の2つの利点 | |
|---|---|
| (1) | 妨害波(雑音・ノイズ)に強い |
| (2) | 通信の秘匿性が高い |
そして、スペクトラム拡散には2種類あるようだ。
| 2種類のスペクトラム拡散方式 | |
|---|---|
| FH | 周波数ホッピング |
| DS | 直接拡散方式 |
本の説明を読んだり、ネットなどを調べてみた。 ノイズに対抗する無線LANのスペクトラム拡散とは?(ASCII.jp) まずは周波数ホッピング(FH)から。
| 周波数ホッピング |
|---|
 |
| デジタル信号をある周波数帯域幅の信号に変換する。 |
そして時間ごとに周波数を変更してデータを送るという。
| 時間ごとに周波数を変更してデータを送信 |
|---|
 |
|
時間毎に上図のように周波数を変更して信号を送る。 周波数がコロコロ変わる事で、盗聴されにくい利点がある。 |
そして時間毎に周波数を変更する事で、別の利点があるのだ。
| 周波数を変更する利点 |
|---|
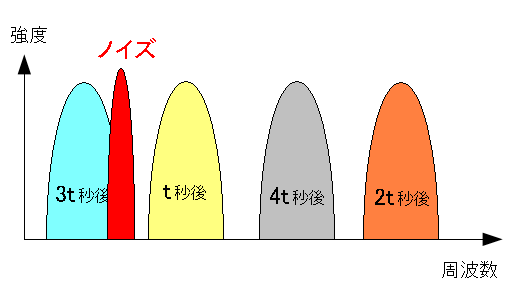 |
|
ある周波数帯域で妨害波(雑音・ノイズ)が発生していても、その周波数帯域で 信号を送る時間は、短時間なので、妨害波に影響されるのが少ない。 妨害波(雑音・ノイズ)対策ができるというのだ。 |
次に直接拡散(DS)を見てみる。 周波数ホッピングと同様に、デジタル信号を、ある周波数帯域幅の 信号に変換する。
| 直接拡散方式 |
|---|
 |
| デジタル信号をある周波数帯域幅の信号に変換する。 |
そして、より幅広い周波数帯域幅の信号に変換する。
| より幅広い周波数帯域幅の信号に変換 |
|---|
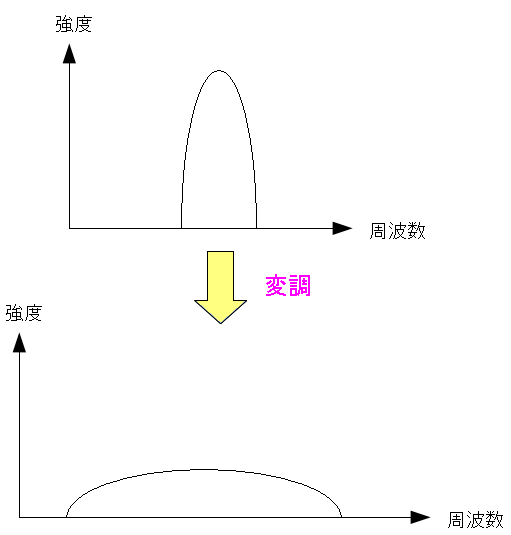 |
|
平べったい感じの信号になる。 これだと通信なのかノイズなのか見分けが難しいため 通信されにくい利点がある。 |
そして、妨害波(雑音・ノイズ)が発生した時にも強みを発揮する。
| 妨害波(雑音・ノイズ)対策 |
|---|
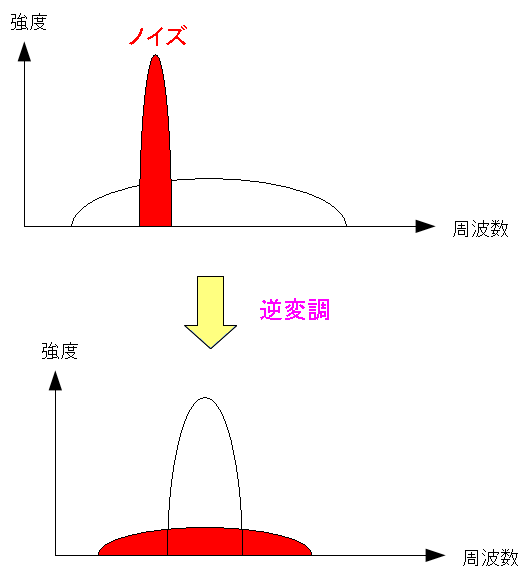 |
|
妨害波(雑音・ノイズ)がのっても、データを復元(逆変調)する際、 妨害波(雑音・ノイズ)は拡散してしまうが、元のデータは復元されるため 妨害波(雑音・ノイズ)が除去される形になる。 |
ところで直接拡散だと妨害波(雑音・ノイズ)が除去されるのか 少し踏み込んだ仕組みについては・・・ そんなん、わからへん! なのだ。 本の受け売りを書いているのすぎないのだ!! という事で、この時は、そのまま無視して前に進む事にした。 直接拡散の仕組みや、妨害波(雑音・ノイズ)の除去の仕掛けは 後述しています。OFDM変調
5.2GHz帯域の電波を使う場合、OFDM変調を使うという。 どんな物なのか調べてみると、日経ITproのサイトが出てきた。 無線LANでデータを送受信する仕組みをやさしく説く(5) 伝送速度と変調方式 まずは以下のように、一次変調したデータを分割する。
| OFDMとは |
|---|
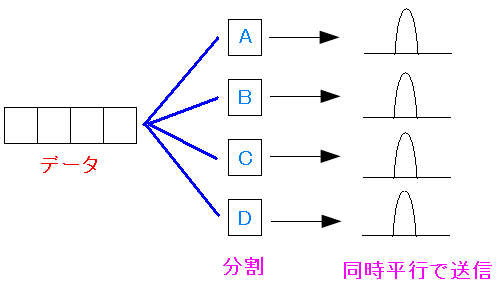 |
|
まずは1次変換したデータを分割する。 そして分割した物を同時並行で送信する。 データを運ぶ経路が増えているので、データ送信速度が速くなるのだ。 |
どのように並行して送信しているのか。
| OFDMは周波数分割 |
|---|
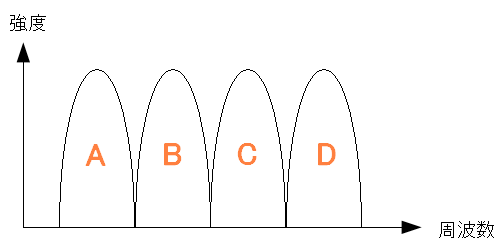 |
|
周波数を軸にとると、綺麗に整列させているのだ。 |
他にも、マルチパスに強いという話が書いていた。
ところで・・・
マルチパスとは何やねん?
なので調べてみた。
| マルチパスとは |
|---|
 |
|
「Multi-Path」の意味だという。直訳すると「複数の経路」になる。 電波は四方八方に飛ぶため、無線アクセスポイントから出た電波は 直接、パソコンへ向かう物もあれば、壁などの障害物に反射し パソコンに向かう物もある。 直接波と反射波という複数の電波を受信する事をマルチパスという。 |
そしてマルチパスと一緒に出てくる言葉として 「フェイジング」がある。
| フェイジングとは |
|---|
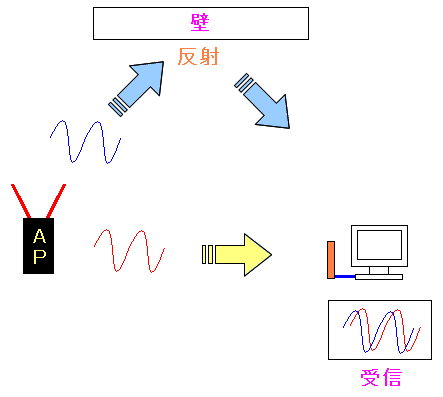 |
|
「Fading」の意味だという。「Fade」の現在進行形で 減衰とか色褪せるの意味だ。 反射波の場合、直接波よりも少し長い経路を飛んでくるため 遅れてやってくる。そのため、波形が歪んだりする。 それをフェイジングと呼ぶ。 |
だが、本の説明や、ASCII.jpのサイトに載っているOFDNの説明を見ても・・・ いまいち、よくわからん だった。 わかったような、わからん状態である事は、まさに・・・ 全く理解してへん なのだ。 理解する事を断念し、前に進む事にした。 OFDMについては後述しています。 ますます混乱する そして本には個々サブキャリアとして BPSK,QPSK,16-QAM,64-QAM変調 が使われているという。 サブキャリアって何やねん? だった。 そしてスペクトラム拡散以外にも、BPSKやQPSK変調など 色々な変調が出てきたので、混乱してきた。
| たまには自己弁護 |
|---|
|
サブキャリアを日本語に訳すると「搬送波」になる。 昔、短波ラジオにハマっていた時期があったので 「搬送波」という単語は知っていたのだが カタカナで書かれると、何の事か、わからなかったのだ。 |
デジタル信号を電波を送る仕組み
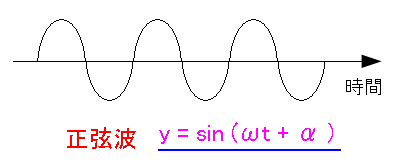
デジタル信号を、そのまま電話線や電波として 送信する事はできない。 デジタル信号を加工する必要がある。 ところでISDNや光回線などが登場する以前、 アナログの電話回線を使って、インターネット接続する時、 データの変換装置として モデム が良い例だった。 デジタル信号を、アナログ回線で送信するために アナログ信号に変換して送信していたのだ。 無線(電波)の場合でも同じ事が行なわれているのだ。 そこで電波の話を調べてみる事にした。 音声やデジタル信号を電波に乗せるために 変調 が行なわれるのだ。 一番わかりやすいのはAM変調なので、AM変調を例にして 変調が何なのかを説明してみる事にした。AM変調
AM変調。AMという文字を見るとラジオのAMを連想しそうだが まさに・・・ ラジオのAMなのらー なのだ。 まずは送りたい音声信号があるとする。
| 送信したい音声信号 |
|---|
 |
|
だが、音声信号を、このままでは電波として信号を 離れた所へ伝える事ができない。 |
そこで、音声信号を運搬する波(搬送波)が必要になる。
| 搬送波 |
|---|
 |
|
音声信号やデジタル信号を運搬する波(搬送波)は 正弦波なのだ。 |
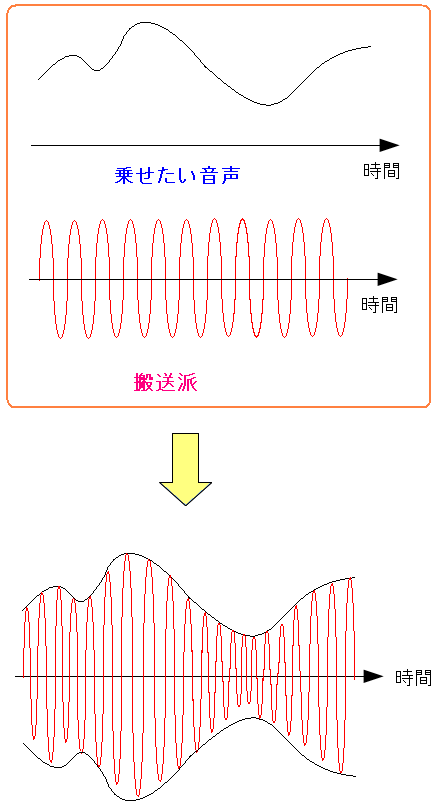
音声信号と搬送波を組み合わせた波を電波として送信する事で 空間中を情報が伝わっていくというのだ。
| 音声信号と搬送波を組み合わせて送信する |
|---|
 |
|
音声信号の振幅に合わせて、搬送波が送られる。 搬送波の波長が短いので、搬送波が音声信号を表現している。 |
AM変調の話が出たが、その他の変調を見ていく事にする。ASK変調
ASK変調とは Amplitude Shift Keying の略だ。 振幅変調の事を言う。
| デジタルデータを変調する方法 (ASK変調) |
|---|
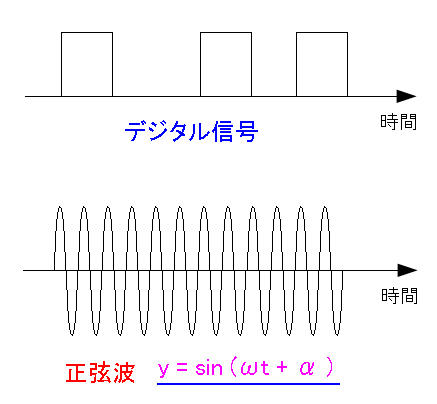 |
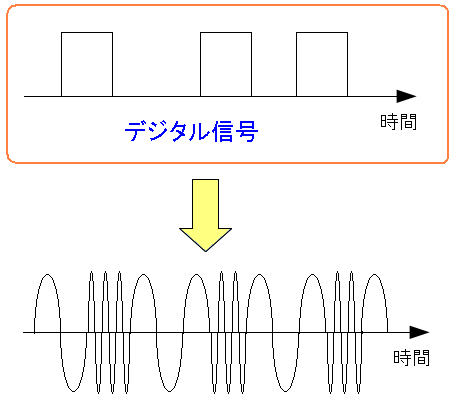
| デジタル信号を、正弦波に乗せて送信する方法だ。 |
具体的に、どう乗せるのかを図にしてみると、次のようになる。
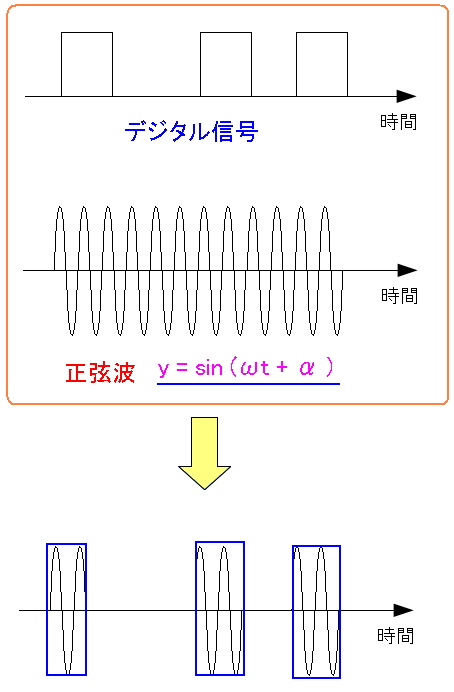
| ASK変調とは |
|---|
 |
|
振幅変調なのでデジタル信号が「0」の時は 搬送波の振幅「0」にして、デジタル信号が「1」の時は 搬送波の振幅を「1」にする方法だ。 |
だが、ASK変調には2つの問題点がある。
| ASK変調の問題点(1) |
|---|
 |
|
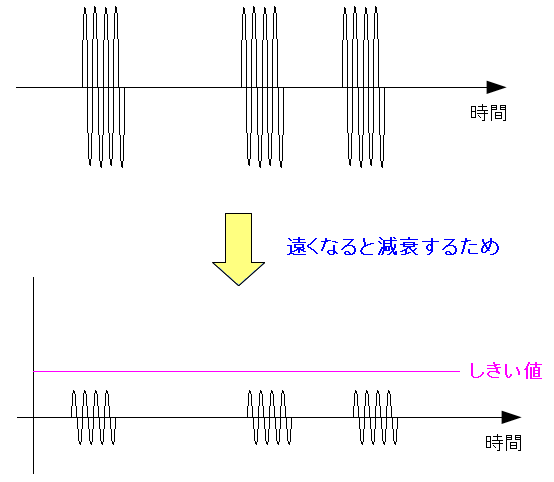
信号は遠くへ行けばいくほど減衰してしまう。 「0」と「1」を判定するための、しきい値の設定だが しきい値を高く設定すると、「0」か「1」を判別できない場合がある。 |
もし、しきい値が低いと、次の問題も出てくる。
| ASK変調の問題点(2) |
|---|
 |
|
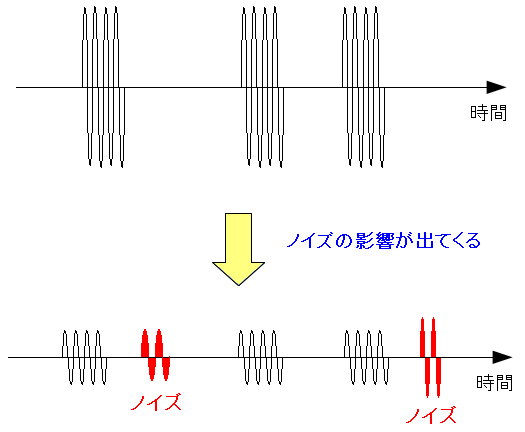
信号にノイズが乗った場合だ。 信号が減衰しているため、ノイズと同じ大きさの場合 信号の減衰に合わせた、しきい値を使うと、 ノイズを「1」と認識してしまう。 |
FSK変調
FSK変調とは Frequency Shift Keying の略だ。 周波数変調の事を言う。
| FSK(周波数変調)とは |
|---|
 |
|
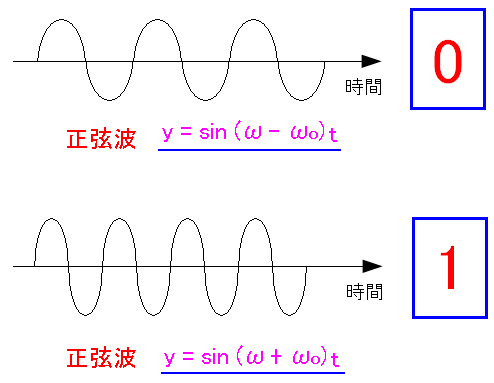
デジタル信号が「0」と「1」の違いを 搬送波の周波数を変える事で、搬送波に乗せる方法だ。 |
具体的に示すと以下のようになる。
| FSK(周波数変調)でデジタル信号を送信する方法 |
|---|
 |
|
デジタル信号に対応させて、搬送波の周波数を変更させて 送信する方法だ。 |
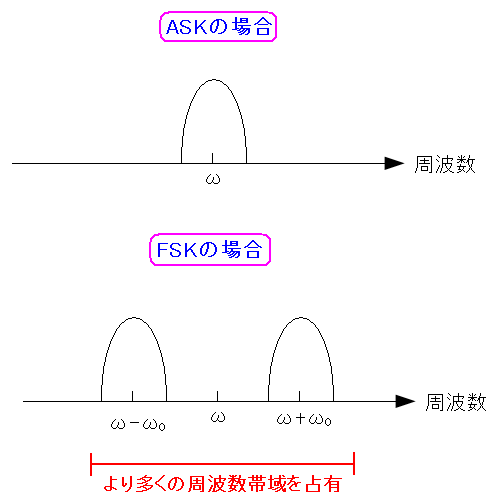
FSK変調の場合、周波数の違いで「0」と「1」を区別するため 信号が減衰しても、しきい値の問題は発生しない。 だが、問題点がある。
| FSK変調の問題点 |
|---|
 |
|
FSK変調は2つの周波数を使うため、ASK変調よりも広い範囲の 周波数帯域を使う。そのため限られた周波数の有効活用に反するのだ。 |
PSK変調 (BPSK変調)
PSK変調とは Phase Shift Keying の略だ。 位相変調の事を言う。
| 位相変調(PSK)とは |
|---|
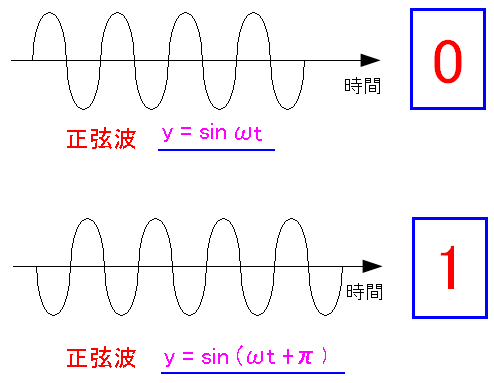 |
| 位相変調とは、搬送波の位相をズラす事で「0」と「1」を送る方法だ。 |
PSK変調の事を、BPSK変調とも言うのか。
「1」と「0」の2つの値を取る事から
Binary PSK (2値PSK)
なのだ。
具体的には以下のようになる。
| 位相変調(PSK)でデジタル信号を送る方法 |
|---|
 |
|
搬送波の位相をズラす事で「0」「1」のデジタル信号を 送信する方法だ。 |
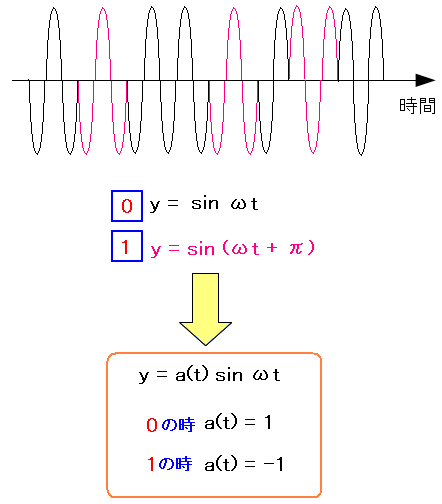
ところで位相を180度ズラす事は、搬送波の式を以下のように表現できる。
| PSK変調における搬送波の式 |
|---|
 |
|
位相が180度ズレるため、「0」の時はa(t)=1にして 「1」の時は、a(t)=-1と決めれば、1つの式で表現できる。 |
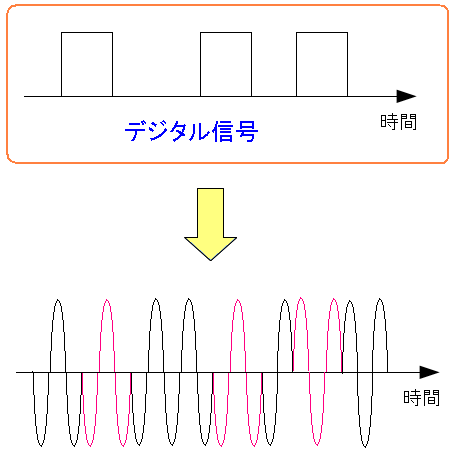
位相のズレで「0」と「1」を表現する方法だ。 位相変調の概略は以下のようになっている。
| PSK変調の発信側の概略図 |
|---|
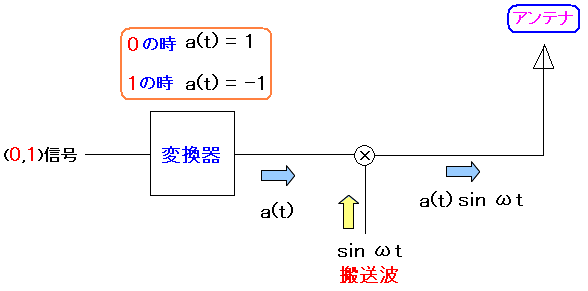 |
|
デジタル信号を変換器で「1」と「-1」の信号に変換する。 そして搬送波のsin(x)と掛け合わせる事で、位相変調が行なえる。 |
ところで受信側の仕組みだが、位相のズレの検出方法は、 以下のような仕組みになっている。
| PSK変調の検出について |
|---|
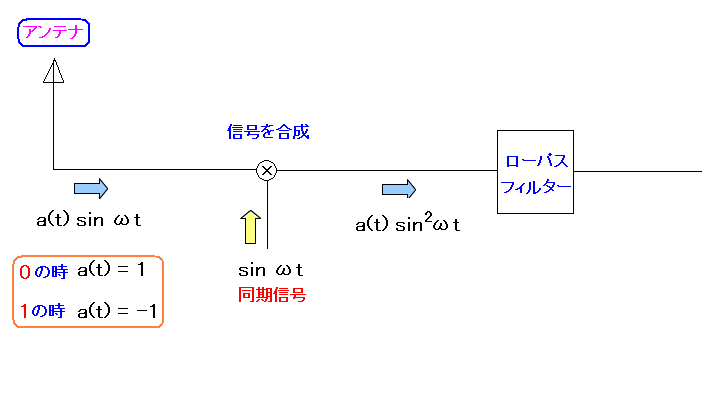 |
| 搬送波を捕らえた後、同期信号と合成を行なう。 |
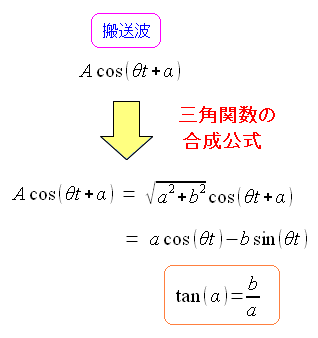
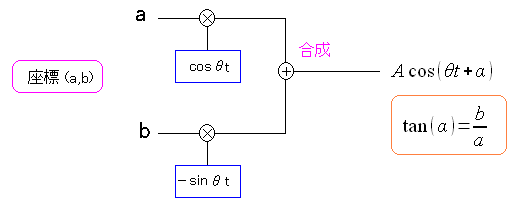
ここで三角関数の公式が出てくる。
| PSK変調の検出について |
|---|
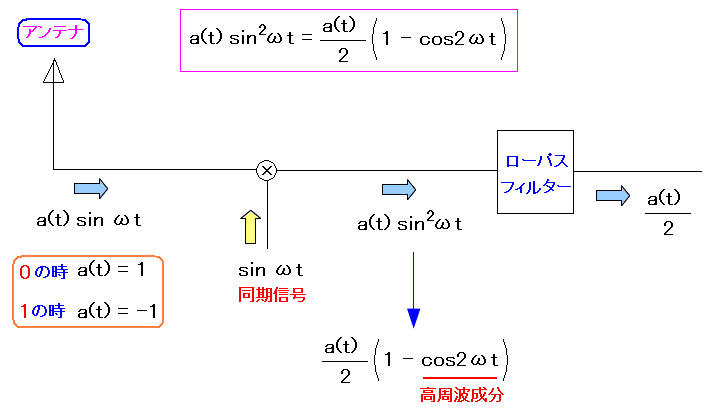 |
|
同期信号と合成した公式を、三角関数の2倍角公式に当てはめると 、a(t)成分(1か-1)と高周波成分に分離できる。 ローパスフィルターを使って、高周波成分を取り除けば a(t)の成分のみが取り出せる。まさにデジタル信号部分だ。 |
ローパスフィルターとは、低周波成分だけ通す回路だ。
Low Pass filter (LPF)
という。
仕組みは以下の通りになる。
| ローパスフィルターの仕組み |
|---|
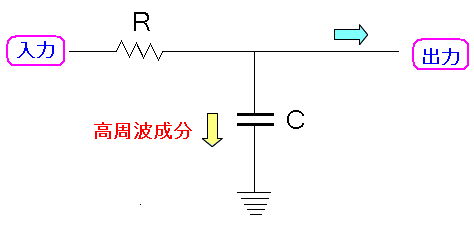 |
|
コンデンサーは高周波を通しやすい性質がある。 コンデンサーを使って、高周波だけ逃す回路にすれば良いのだ。 |
ローパスフィルター(LPF)が高周波を除去する話については 後述しています。 PSKは、FSK変調のような周波数の占有の問題もなければ、 ASK変調の、しきい値の問題もない。 だが、別の問題がある。
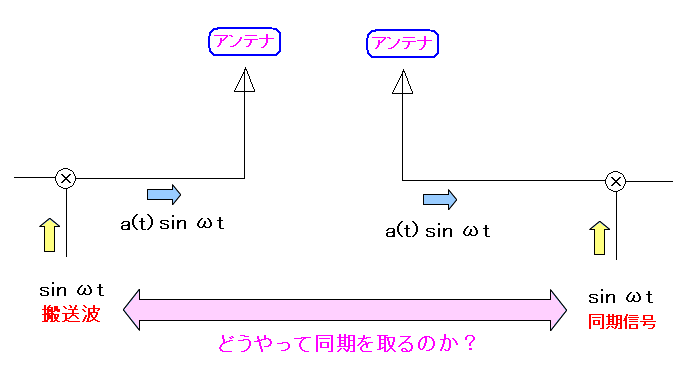
| PSKの問題点 |
|---|
 |
|
受信側で、a(t)成分を取り出すために、同期信号を使うのだが 搬送波と同期を取る必要があるが、どうやって同期をとるかが問題だ。 |
短所をなくそうとしたら、別の短所が出てしまう。 そこで同期信号の問題を解決したのがDPSKなのだ。DPSK (DBPSK)
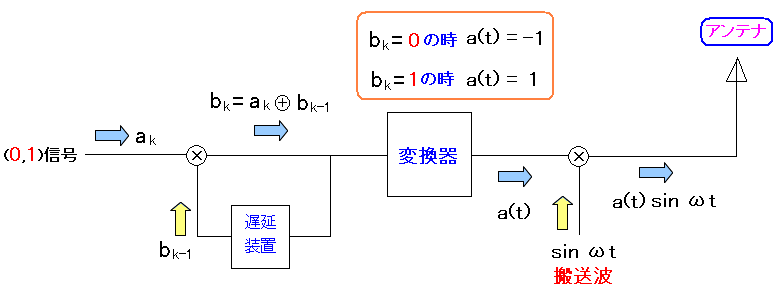
DPSKとは Differential Phase Shift Keying の略で、日本語にすると 差分位相偏移変調 なのだ。 一体、どういう物なのか。 DPSKでの送信の仕組みから見てみる事にした。
| DPSKでの送信の仕組み |
|---|
 |
|
最初の部分で、送りたいデジタル信号と、それを遅延させた信号を 合成している。ここが差分位相変調(DPSK)の重要な部分になる。 「差動符号化器」と呼ばれる部分だ。 あとは、搬送波に乗せて電波として、信号を送るのだ。 |
肝になる差動符号化器を詳しく見てみる。
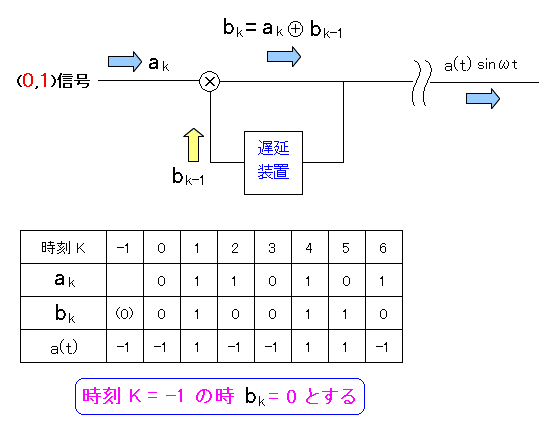
| 差動符号化器 |
|---|
 |
|
上図のように、排他的論理和を使って、信号を変換する。 変換された信号が、1つ後の送りたい信号との合成に使われる。 言葉では表現しにくいのだが、図式化すると上のようになる。 |
言葉では説明しにくい方法で、データ変換している。 その理由は、復元側(受信側)での復元をしやすくするためにあるのだ。
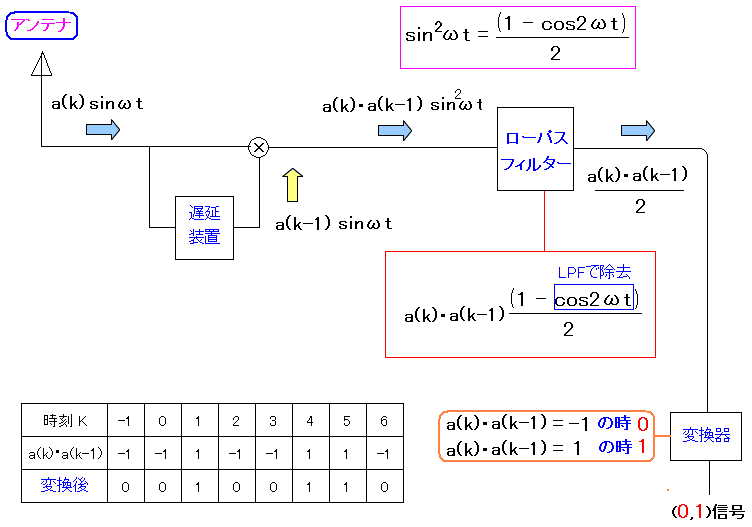
| DPSKでの受信側(復元側)の仕組み |
|---|
 |
|
PSKとの違いは、DPSKの場合、同期をとる信号が不要な事だ。 そして受信した信号を、すぐに差動符号化器を通しているのだ。 この装置があるお蔭で、同期をとる信号が不要になるのだ。 |
そして送信の際のデータ変換と、受信部分でのデータ復元を見比べてみる。
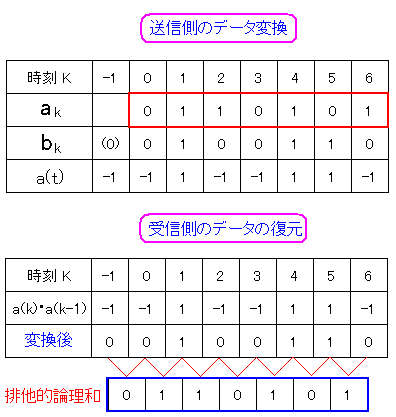
| 送信の際のデータ変換と、受信部分でのデータ復元の比較 |
|---|
 |
|
受信側で最終的にできた信号を、前後の値で排他的論理和を求めると 元の信号に復元できるのだ。 このように、送信側で遅延を利用してデータを変換し 受信側でデータの復元する方法を「遅延検波」というのだ。 |
いかにも簡単に説明している感じだが・・・ 七転八倒しながら理解したのだ だった。 だが、わかりやすい資料のお蔭で、なんとか理解できたのだ。 通信理論 第3回 電子情報工学科(九州工業大学) ところで、近年ではDPSKの事を PSK (BPSK) と呼んでいる事が多い。 なので無線LANの変調で、PSK(BPSK)といえば、実際の所は DPSK(DBPSK)の事を指しているのだ。QPSK
PSKの拡張版だというのは、名前から推測できる。 QPSKとは Quadrature PSK なのだ。
| 「Quadrature」の意味 |
|---|
|
「方形の」とか「求積法」、「直交」などの意味がある。 4つの方向(十字の直交)から、4つの値を取るという意味になっている。 |
PSK(BPSK)では位相を180度ズラす事で、同じ周波数の搬送波でも
「1」と「0」を表現していた。
QPSKでは
位相を90度づつズラして、4値を表現する
というのだ。
図式化すると以下のようになる。
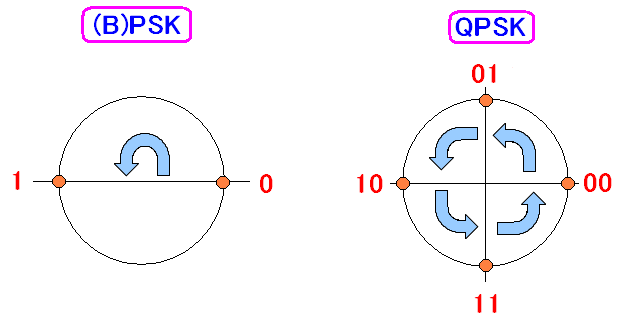
| PSK(BPSK)とQPSKとの違い |
|---|
 |
|
BPSKだと180度の位相のズレを使って「0」と「1」を表現する。 そのため一度に1ビットしか送れない。 QPSKだと90度の位相のズレを使って「00」「01」「10」「11」を表現する。 そのためで1度に2ビット送信できる。 |
QPSKは2ビットの送信可能
という事でPSKと比べて2倍のデータ送信ができる。
QPSKの位相のズレと値を表にすると、わかりやすい。
| QPSKの位相と値について | |
|---|---|
| 位相のズレ | 値 |
| 0度 | 00 |
| 90度 | 01 |
| 180度 | 10 |
| 270度 | 11 |
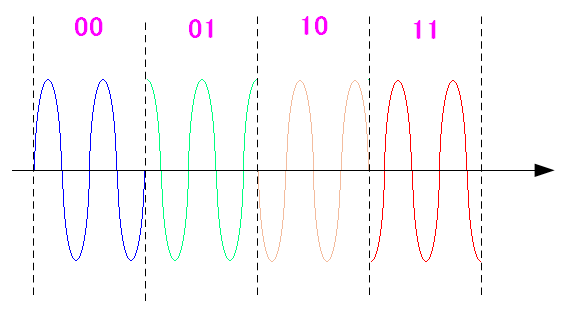
実際に正弦波で見ると、次のようになる。
| 正弦波でみたQPSKにおける値と位相のズレとの関係 |
|---|
 |
QAM
もっとデータ送信ができる方法がないのかという事で 考え出されたのがQAMだ。 QAMとは・・・ Quadrature Amplitude Modulation の略なのだ。 だが、これだけだと・・・ 何の意味か、わからへん! なのだ。 日本語訳では 直角位相振幅変調 なのだが・・・ これでも、よくわからん なのだ。 そこで言葉の意味を無視して、どんな物か調べてみる事にした。 ASKは振幅を使って値を表現していた。 PSKとQPSKでは位相のズレを使って値を表現していた。 QAMとは、振幅変調のASKと、位相変調のPSK、QPSKの両方の方法を 合体させた物だ。 つまり・・・ 振幅と位相のズレで値を表現する というのだ。 振幅と位相の両方を使う事で、1度により多くの情報量を送信するのだ。 つまり以下のような事だという。
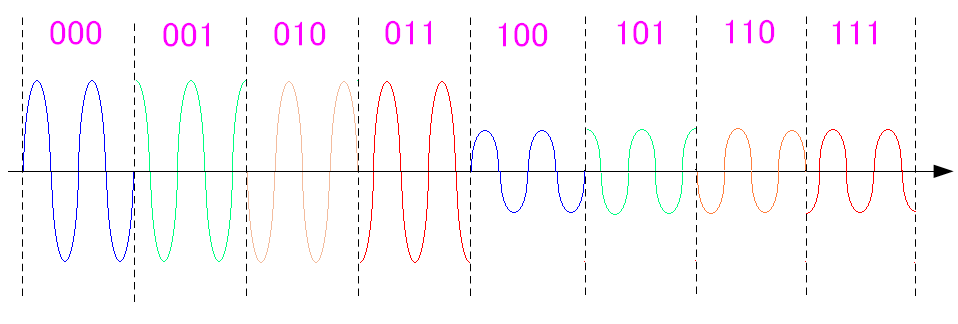
| 振幅と位相のズレで値を表現する方法 |
|---|
 |
|
PSK変調に2種類の振幅を加えた場合、8通りのデータ表現ができ 3ビットのデータが送信できるのだ。 (注意) ここでは、あくまでも例なので、ビットの値は、私が適当に決めた物だ。 |
ところでQAMでも、16QAM、64QAM、256QAMがある。 こんな違いがあるという。
| QAMの種類と1度の送信できる情報量 | |
|---|---|
| 種類 | 1度に送信できるビット数 |
| 16QAM | 4bit (2の4乗 = 16) |
| 64QAM | 6bit (2の6乗 = 64) |
| 256QAM | 8bit (2の8乗 = 256) |
QAMの前にある数字は、振幅と位相のズレでできる 組み合わせ数の事を差すのだ。 わかりやすい説明が書いているサイトを見つけた。 わかりやすいモバイルブロードバンド(ワイヤレスブロードバンド) 変調方式 QAM(カム) まずは16QAMから見る事にした。
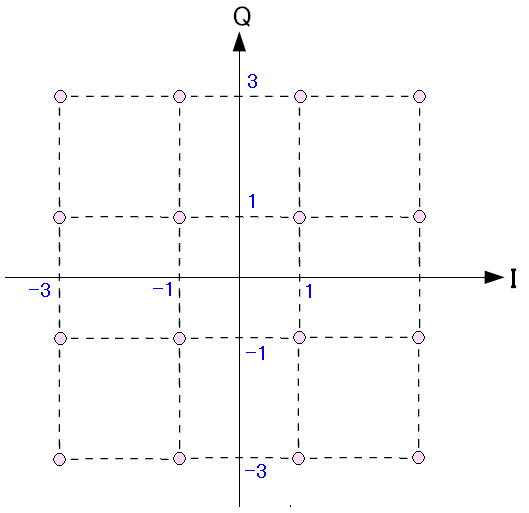
| 16QAMの信号星座図 |
|---|
 |
|
振幅と位相の関係の配置図だ。 この図の事を信号星座図や信号空間ダイヤグラムと呼ぶ |
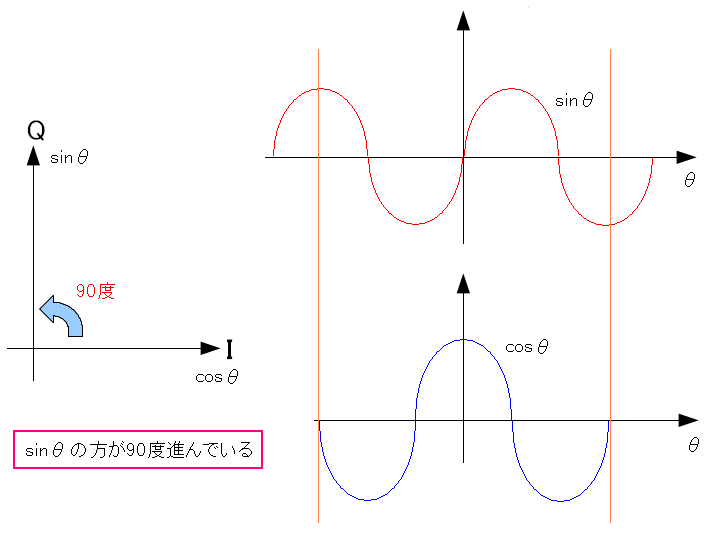
ところで信号星座図の座標軸は (X,Y)でなく(I,Q)やねん! と思った。 そしてX軸に当たるI軸はcosΘ成分で、Y軸はsinΘ成分というのだ。 だから何やねん! やっている意味がわからん。 だが、調べてみても、説明しているサイトが見つからなかった。 だが、以下のサイトにヒントがあった。 QAM - 通信用語の基礎知識 つまり次のような事だった。
| 信号星座図ではI軸はcosΘで、Y軸はsinΘ |
|---|
 |
|
まずは「Θ」は搬送波の周波数である事だ。 これに気づかないと、この図が読めなくなる。 cosΘとsinΘでは90度の位相のズレがある。 そのため座標軸にするには、最適だ。 |
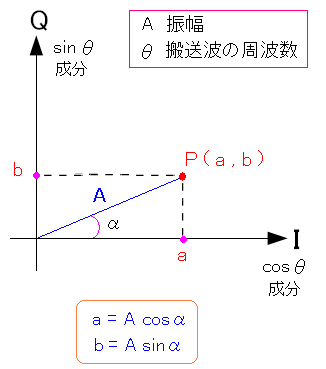
単に位相のズレが90度という理由だけではない。 搬送波は位相のズレがあるため、cosΘ成分とsinΘ成分に 分解する事ができるのだ。
| 位相のズレがあるため、cosΘ成分とsinΘ成分に分解する事ができる |
|---|
 |
|
点Pの位置の振幅と位相のズレの搬送波の場合 cosΘ成分とsinΘ成分に分解する事ができる。 |
位相のズレのαは三角関数合成の式より導き出せる。
| 位相のズレのαを導く |
|---|
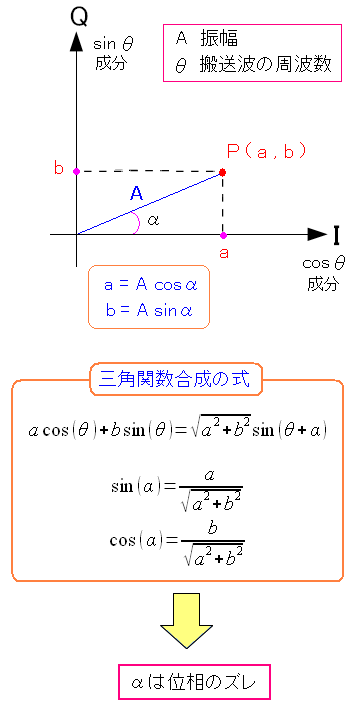 |
| 三角関数の合成式を使えば「α」が求まる。 |
信号星座図(信号空間ダイアグラム)は、振幅と位相のズレの両方を 一目でわかるための図なのだ。 では、16QAMの信号星座図を見てみる。
| 16QAMの信号星座図 |
|---|
 |
上図の第一象限を取り上げてみる事にした。
| 16QAMの信号星座図の第一象限 |
|---|
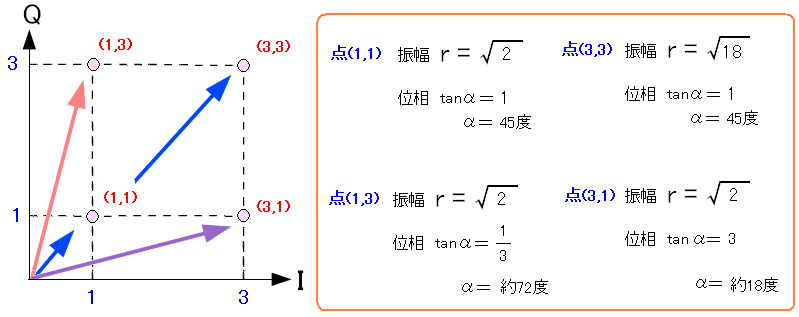 |
|
16QAMでは第一象限に4つの座標を置いている。 (1,1)、(1,3)、(3,1)、(3,3)だ。 そこから位相のズレに当たる「α」と振幅が求まる。 |
全体を見てみる事にする。
| 16QAMの信号星座図 |
|---|
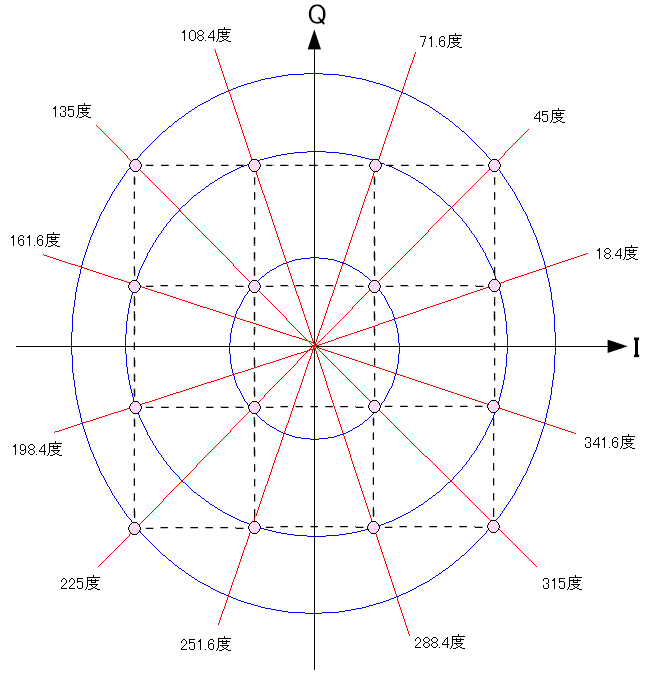 |
|
3種類の振幅を使っているのがわかる。 12種類の位相のズレを使っているのがわかる。 |
すごく見通しが良くなった
のだ。
次に64QAMだが、以下のような信号星座図になっている。
| 64QAMの信号星座図 |
|---|
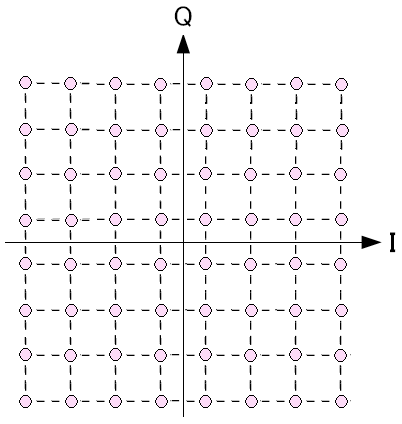 |
|
各象限に16個づつ点がある。 一度に6ビットのデータ送信ができる。 |
そして256QAMを見る
| 256QAMの信号星座図 |
|---|
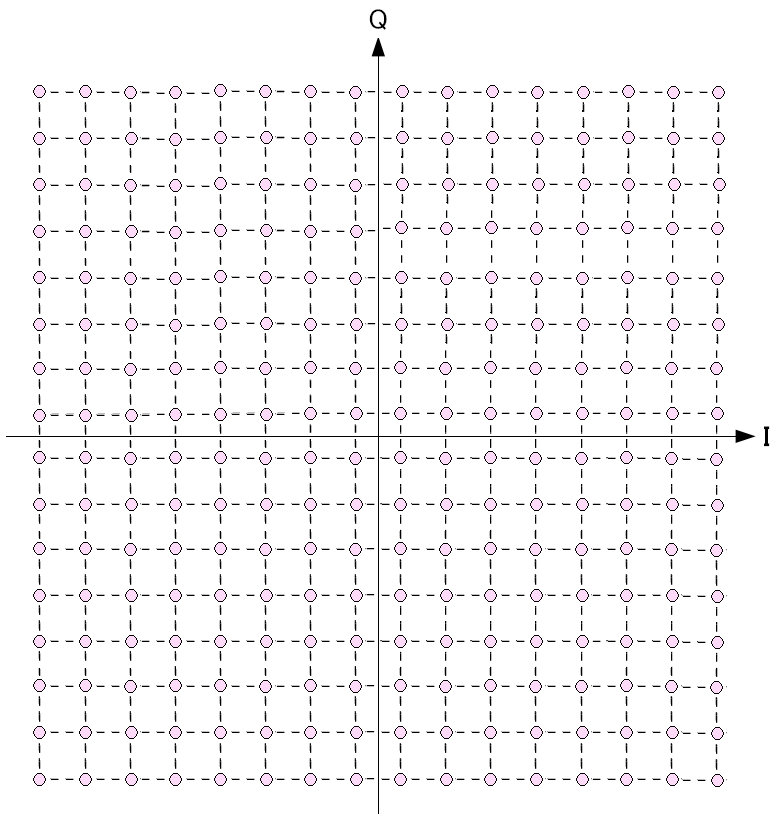 |
|
各象限に64個づつ点がある。 一度に8ビットのデータを送信できる。 |
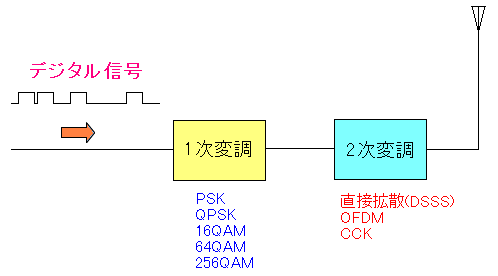
ところで、256QAMが実用化されたのは、最近の話だ。 なぜなら・・・ 誤差が許される範囲が狭いため・・・ 送信誤り問題があった というのだ。1次変調、2次変調
ASK変調、PSK変調、直接拡散変調にOFDM変調など、 色々な信号変調があるのを知った。 これだけ変調の種類あると、覚えきれないし、ややこしいし、 わけがわからんようになる。 そんな中、以下のサイトを見て、なるほどと思った。 変調のはなし(2)|Wireless・のおと|サイレックス・テクノロジー株式会社 このサイトを見て・・・ 1次変調、2次変調があるのか! だった。 ここに1次変調、2次変調の違いを書いているサイトがあった。 ASCII.jp:きっちり知りたい無線LANの変調技術の基礎 (3/3)|無線LANのすべて つまり以下の事だという。
| 1次変調と2次変調の違い | |
|---|---|
| 1次変調 | デジタル信号を電波に乗せるための変調 |
| 2次変調 | 妨害波(雑音・ノイズ)や秘匿性を高めるため |
そこで、どの変調方式が1次変調で、どの変調方式が2次変調なのかを 表にしてみた。
| 1次変調と2次変調 | |
|---|---|
| 1次変調 | BPSK、QPSK、16QAM、64QAM、256QAM |
| 2次変調 | 直接拡散方式(DSSS)、OFDM、CCK |
(注意) CCKを一次変調に使う場合があるようです。 |
図式化すると以下のようになる。
| 1次変調、2次変調を経て無線通信が行なわれる |
|---|
 |
| デジタル信号を電波に乗せるため、2回変調を行なっている。 |
デジタル変調とフーリエ展開
本やネットを見ていると、ASK変調のスペクトル分布の話があった。 ASK変調のスペクトラムを取ると以下のようになるという。
| ASK変調のスペクトラム分布 |
|---|
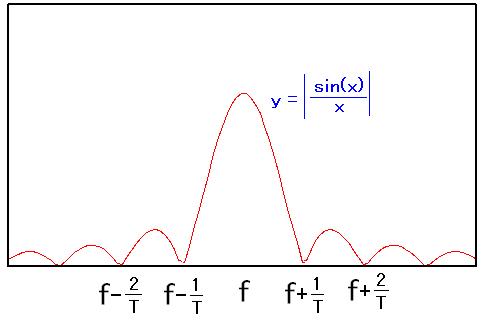 |
|
sin(x) / x の形状を取るという。 ここでは絶対値をグラフにしている。 |
そして中心の山と、その他の山では呼び方が異なるのだ。
| グラフの山の呼び方が異なる |
|---|
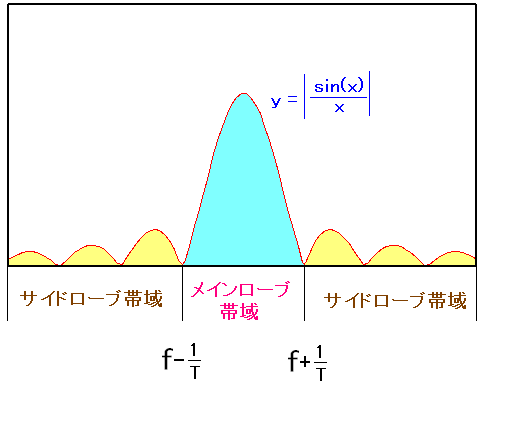 |
|
中心の高い山を「メインローブ」と呼ぶ。 その他の山を「サイドローブ」と呼ぶ。 ローブとは「lobe」だ。その意味は「極大部分」だ。 そのため盛り上がっている山をローブと呼ぶのだ。 |
カタカナが氾濫しすぎて、わけがわからんようになる。 英単語の綴りを調べて、辞書を引くという手間が増える。 最初から中心極大と、周辺極大という風に訳せば良いのに カタカナ信仰には困った物だ。 ところで本では次の事が書いていた。
| 送信するのはメインローブのみ |
|---|
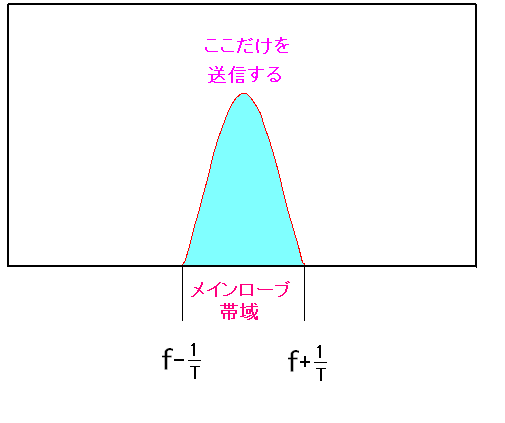 |
|
全領域を送信すると周波数を占有してしまうため メインローブだけを使って送信する場合が多いというのだ。 もし、メインローブだけで送信った場合、不具合が起こるのか? それについては後述しています。 |
さて、ここまでスペクトラム分布を見たのだが 肝心な事を知らなかった。それは・・・ スペクトラムとは何やねん! だった。 だが、なんとなく気づいていた。 フーリエ係数の分布ちゃうか? 色々見ていると、1次変調した信号をフーリエ展開した話などが 載っている。フーリエ展開
ある区間に置いて、どんな関数でも、三角関数の合成で近似できるという。 三角関数の合成に置き換える事をフーリエ展開という。 例えば、以下のパルス波を、三角関数の合成で表現できるのだ。
| パルス波 |
|---|
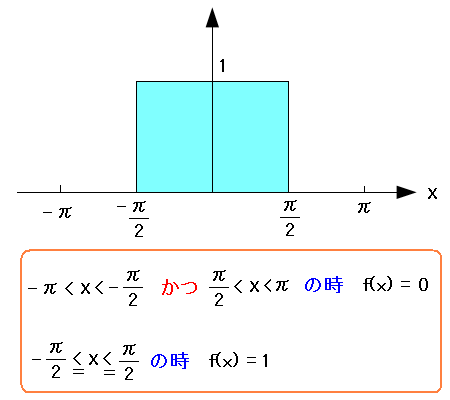 |
フーリエ展開の話だが・・・ 20世紀の記憶を思い出す作業 になった。 学生時代は理系だったし、フーリエ変換は習った。 だが、社会人になって数学とも無縁の世界にいるため フーリエなんて忘れてもうた なのだ。 そこで色々なサイトを見て思い出す事にした。
| フーリエ変換とは |
|---|
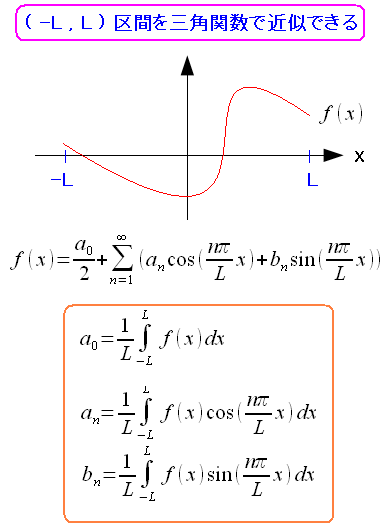 |
|
上図のように、どんな関数でも、ある区間において 三角関数で表現できるというのだ。 上図だと(-L,L)区間におけるフーリエ変換だ。 三角関数の式に変換した物をフーリエ級数と呼ぶ。 茶色で囲んだ部分は、フーリエ級数にある係数の求め方だ。 この係数の事をフーリエ係数と呼ぶ。 もう少し細かい分類をする事ができる。 anをフーリエ余弦係数、bnをフーリエ正弦係数とも呼ぶ事がある。 |
ところで級数とは何か。 昔に習った事は、すっかり忘れてしまっているので 調べてみる事にした。
| 級数とは |
|---|
| ある規則に従って並べられた数、もしくは関数なのだ。 |
ところで、先ほど紹介したフーリエ級数は(-L,L)間の区間という 一般式で表現した物だ。 それを(-π,π)の区間に置き換えると、以下のような表現になる。
| (-π,π)区間のフーリエ級数 |
|---|
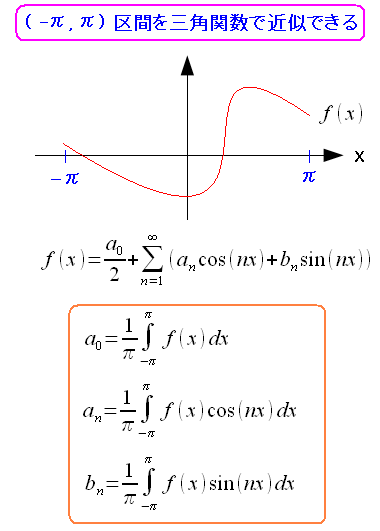 |
| (-π,π)区間だと計算がしやすくなる。 |
計算のしやすさから、今後は(-π,π)区間で考える事にした。 パルス波。(-π,π)区間で考える。
| パルス波を考える |
|---|
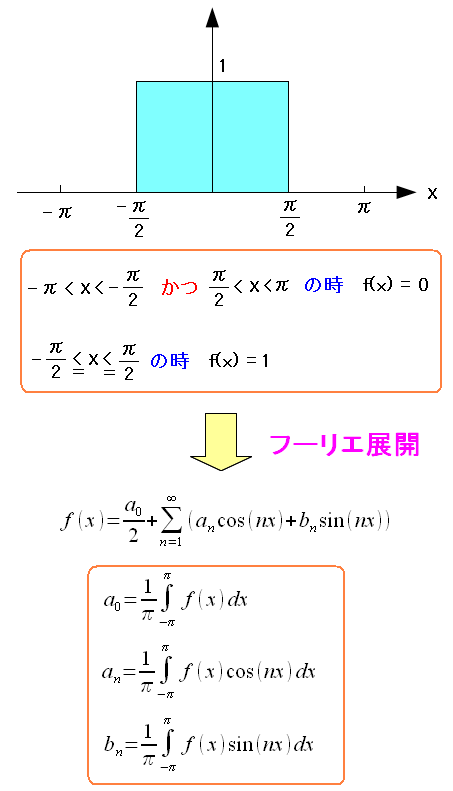 |
このまま、真面目にフーリエ展開をすると、計算が大変だ。 そこで関数の性質を利用して、計算量を減らす事ができるという。 偶関数と奇関数の利用 だという。 でも・・・ すっかり忘れとる のだ。 そこで偶関数と奇関数が何なのかを復習する事にした。
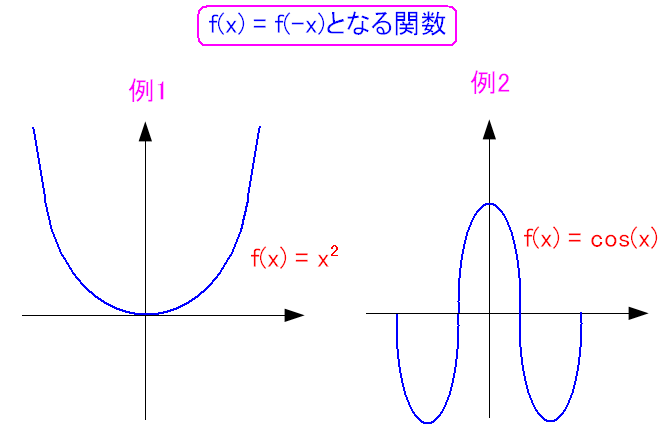
| 偶関数 |
|---|
 |
|
f(x)=f(-x)が成り立つ関数の事だ。 図にすると、Y軸に対して左右対称の関数になるのだ。 |
次に奇関数が何なのかを見てみる事にした。
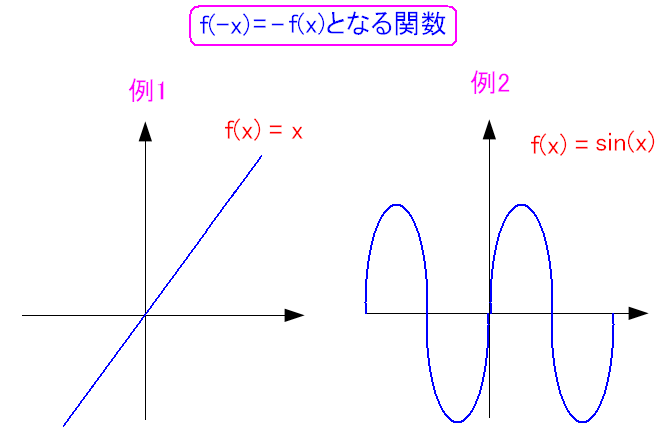
| 奇関数 |
|---|
 |
|
f(-x)=-f(x)が成り立つ関数だ。 上図のように原点(0.0)で対象になっている関数だ。 |
これを踏まえた上でフーリエ級数の式を見てみる。
| フーリエ級数の式 |
|---|
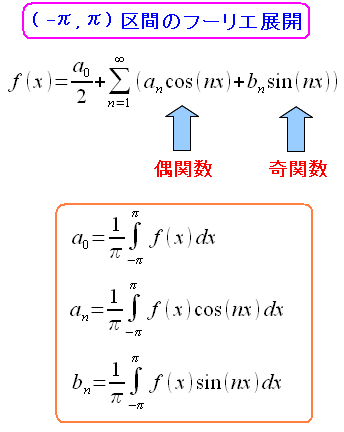 |
| フーリエ級数の式は偶関数と奇関数の合成で構成されている |
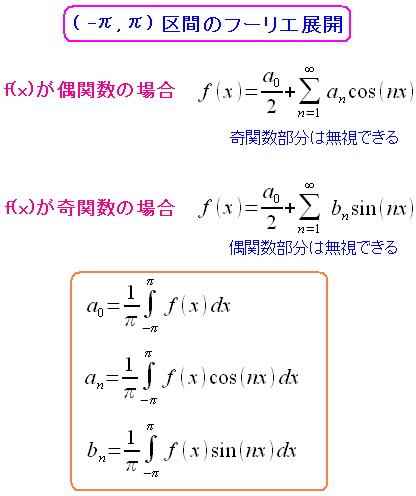
そこでフーリエ展開を行なう際、それが偶関数か奇関数かで 計算量が変わってくるのだ。
| フーリエ展開したい関数 |
|---|
 |
|
もし、関数f(x)が偶関数で、フーリエ展開した場合 フーリエ級数の奇関数の部分を無視する事ができる。 同様に、関数f(x)が奇関数で、フーリエ展開した場合 フーリエ級数の偶関数の部分を無視する事ができる。 |
手抜き計算法ならぬ、計算の簡略化方法を使って 以下のパルスのフーリエ展開をしてみる事にした。
| パルスのフーリエ展開 |
|---|
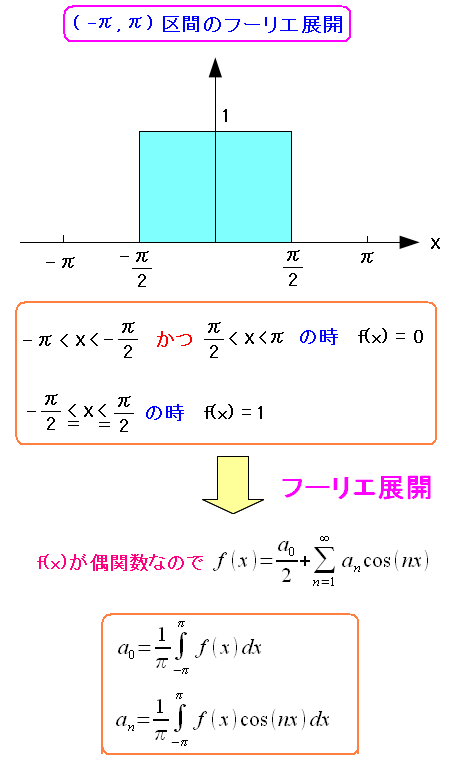 |
|
Y軸に左右対称の関数なので偶関数だ。 そのためフーリエ級数も偶関数の部分のみ求めれば良いのだ。 |
実際にフーリエ展開を行なってみる。
| フーリエ展開 |
|---|
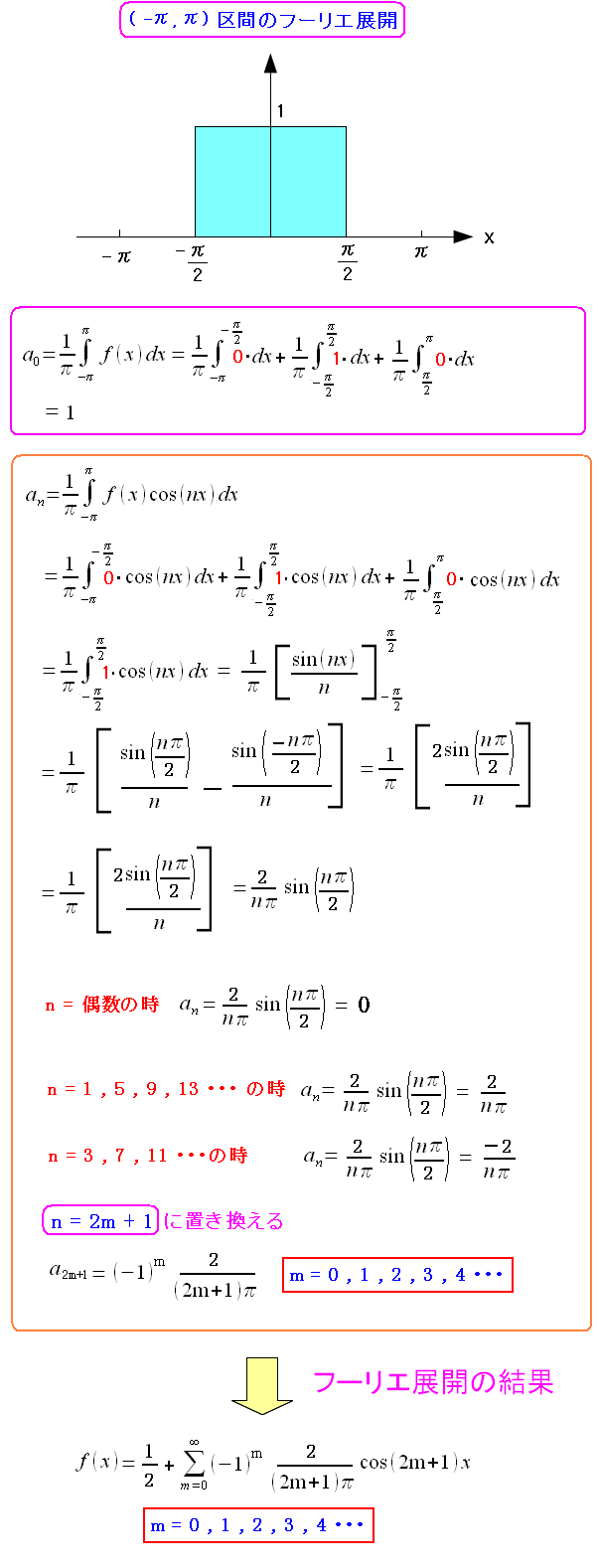 |
| パルスをも三角関数で表現してしまうのだ。 |
実際に、フーリエ展開して求められた式が パルスになっているのか、確かめて見る事にした。
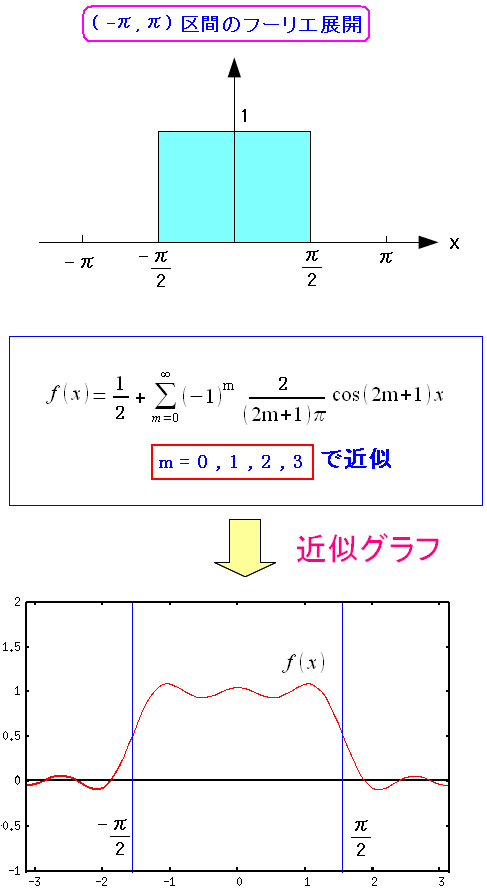
| フーリエ展開した式をグラフにしてみる |
|---|
 |
|
無限級数になってしまうので、mは0〜3までにしてみた。 それでも、かなり良い感じのグラフになっている。 |
ところで本などを見ていると、パルスやASK変調のスペクトラムは sin(x)/xの形を取るという。
| sin(x)/xの形 |
|---|
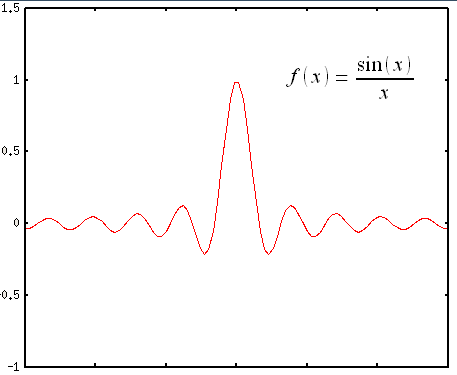 |
| パルスやASK変調のスペクトラムは、sin(x)/xの形を取るという。 |
そこで計算したフーリエ係数を見てみる。
| パルスのフーリエ係数と比較 |
|---|
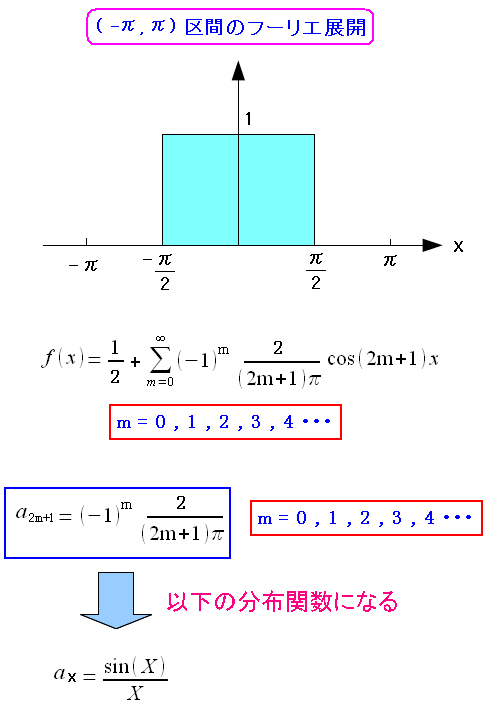 |
| 似ても似つかぬ式になっている。 |
一体、どういう事やねん! そこで調べてみる事にしたが、なかなか見つからない。 途方に暮れそうになった時、何気なくフーリエ係数を求める過程を見ていると ある事に気づいた。 答えが出てるやん! だった。
| フーリエ係数の算出過程を見る |
|---|
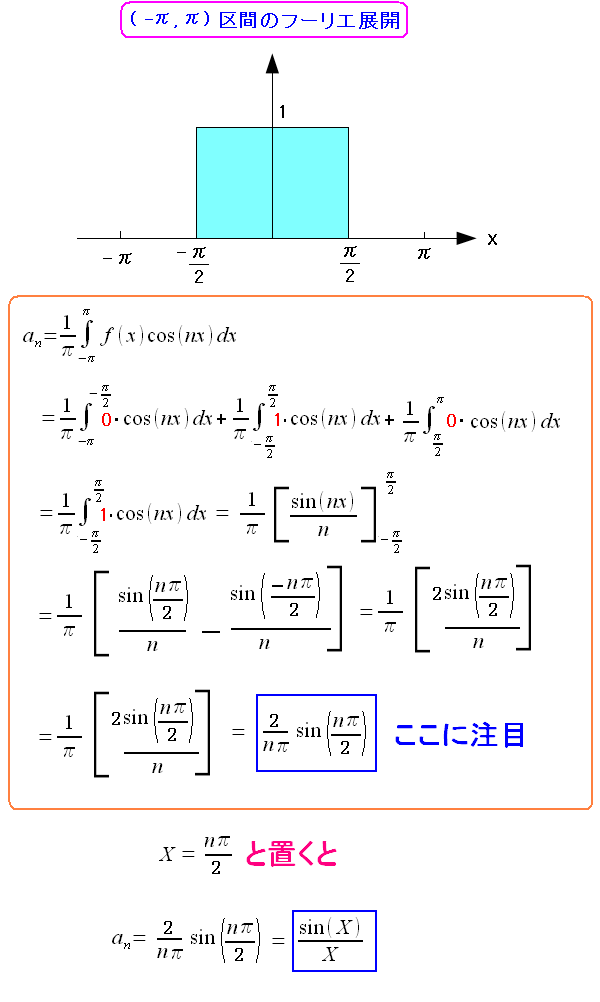 |
| 確かに、フーリエ係数がsin(x)/xの形状になっているのがわかる。 |
さて、sin(x)/xの関数をグラスで眺めてみる。
| sin(x)/xの関数 |
|---|
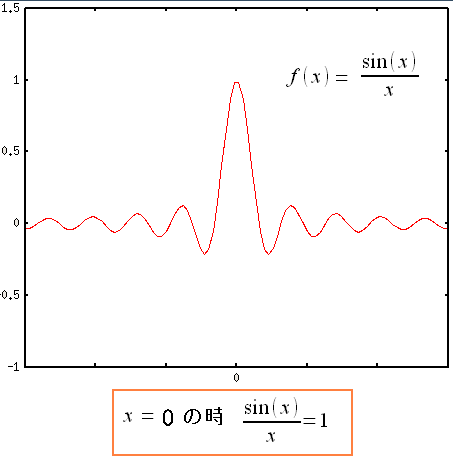 |
| x=0の時、sin(x)/x=1になる。 |
この時、ふと思った。
なんでx=0だとsin(x)/x=1になるねん???
どういう疑問なのか。
| 私が抱いた疑問 |
|---|
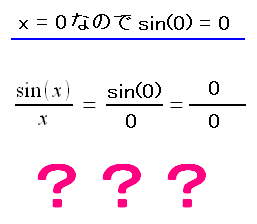 |
|
x=0の時、sin(x)/xは、0/0になってしまう。 0は0で割れない。 |
0/0になりそうな時、極限を考える。
| xを限りなく0に近づけてみる |
|---|
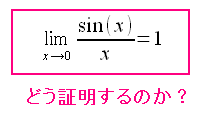 |
|
xを0に限りなく近づけていくと「1」に収束する事を 示す事が必要になる。 |
sin(x)をどう考えるか。
こんな時、ふと思い出した。
テイラー展開や!
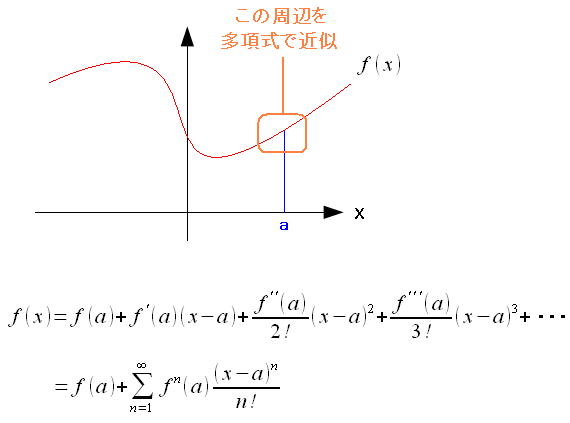
テイラー展開とは以下の事を言うのだ。
| テイラー展開 |
|---|
 |
|
x=aの時、関数f(x)の式を多項式で近似する事ができる。 多項式にする事をテイラー展開という。 |
テイラー展開は一般式だが、x=0の付近で多項式に近似した場合
別の名称で呼ぶ事がある。
マックローリン展開
という。
思い出してくる。昔、習った話を。
| マックローリン展開 |
|---|
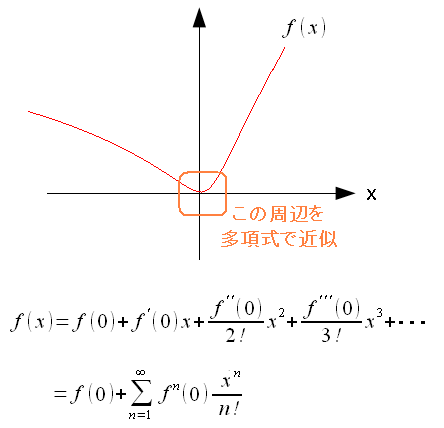 |
|
x=0付近で、関数f(x)の式を多項式で近似する事ができる。 多項式にする事をマックローリン展開という。 やっている事は、テイラー展開と同じなのだが なぜかa=0の時だけ、違う名称で呼ぶのだ。 |
そこでsin(x)関数をマックローリン展開してみる。
| sin(x)関数をマックローリン展開 |
|---|
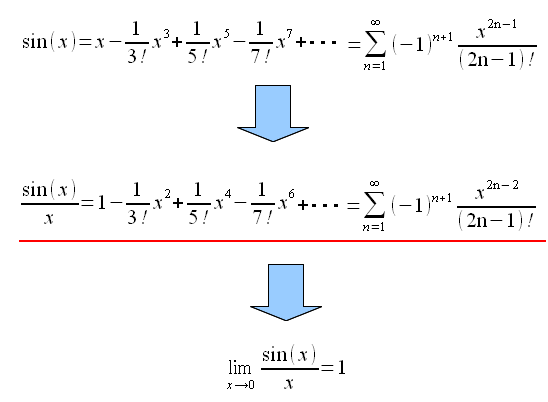 |
| x→0に近づけると、sin(x)/xが1に収束するのがわかる。 |
これで理解できたのだ。
だが、だいぶ後になって、以下のサイトを見る。
ポチの電子回路論
その中で、幾何学を使って証明している部分があった。
そして、文中に・・・
ロピタルの定理
が書いていた。
聞いた事がある名前だ。だが、習った記憶がない。
20世紀の話なので、習ったのか、習っていないのか覚えていない。
そこでロピタルの定理を調べてみた。
| ロピタルの定理 |
|---|
 |
|
ところでロピタルの定理を証明する話もあるのだが そこは割愛します。 |
早速、ロピタルの定理を使ってみる。
| ロピタルの定理を使ってみた |
|---|
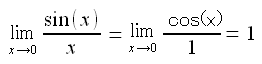 |
|
ロピタルの定理を使って、分子も分母も微分した。 その結果、「1」が導けた。 |
ASK変調 フーリエ展開とスペクトラム分布
パルス波のフーリエ展開を見たのだが、今度はASK変調で フーリエ展開とスペクトル分布(フーリエ級数の分布)を見てみる。
| ASK変調のパルス |
|---|
 |
|
ASK変調とは、振幅の有無で「0」と「1」を区別する方法だ。 考えやすいように(-π,π)区間で「1」の状態を見てみる。 |
早速、フーリエ展開してみる事にした。
| ASK変調をフーリエ展開 |
|---|
 |
ここで計算の省略のため、偶関数の特性を考える。
| >ASK変調をフーリエ展開 |
|---|
 |
|
求めたい関数は、y軸に対して左右対称なので、偶関数だ。 そのためフーリエ展開を行なう際、奇関数部分は無視できる。 |
準備が整ったので、早速、計算してみる。 まずはフーリエ係数を求める。
| フーリエ係数を求める様子 |
|---|
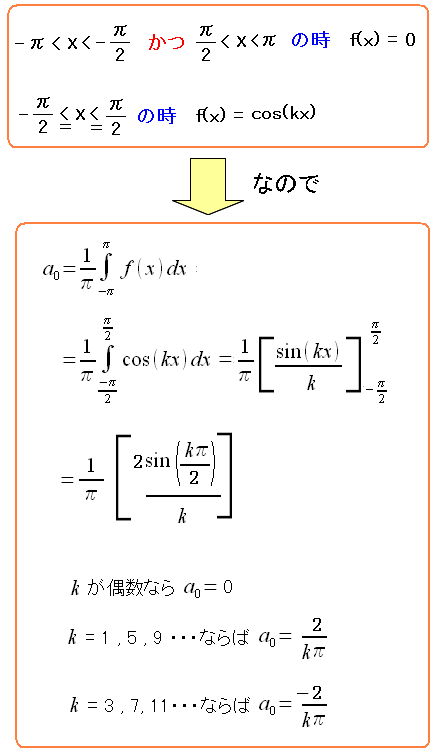 |
次にフーリエ余弦係数を求める。
| フーリエ係数を求める様子 |
|---|
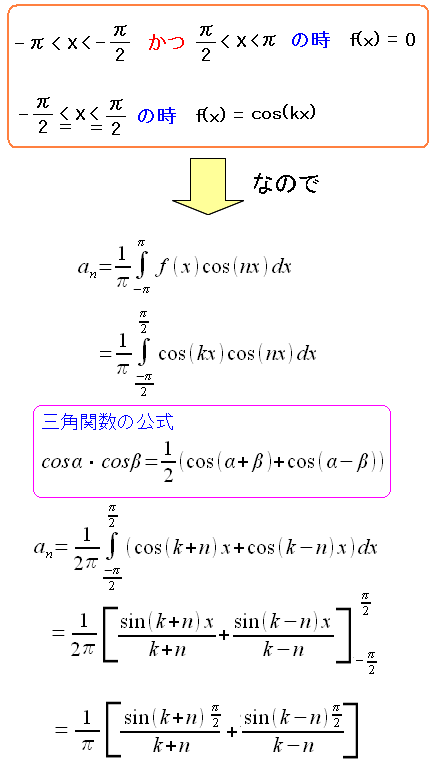 |
| フーリエ余弦係数のanが求まった。 |
そのためフーリエ展開で求まった関数式は以下のようになる。
| ASK変調のフーリエ展開の結果 |
|---|
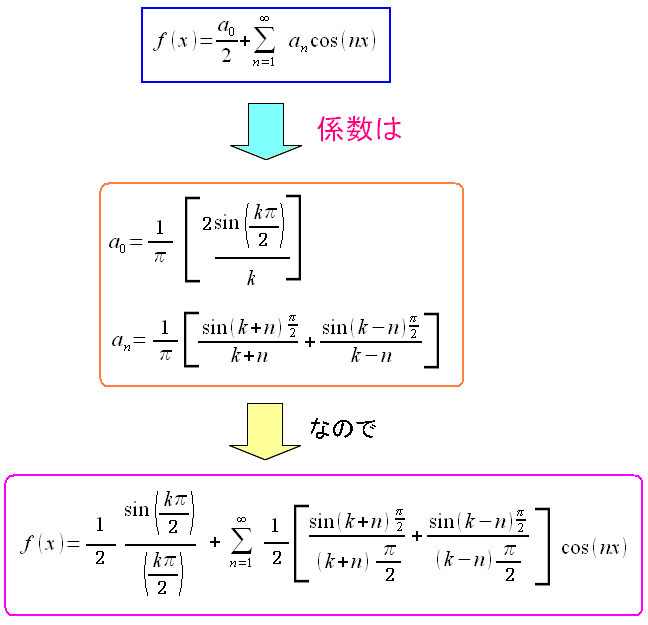 |
この場合、スペクトラム分布は、フーリエ余弦係数のグラフを見れば良いので グラフを取ってみる
| ASK変調のスペクトラム分布 |
|---|
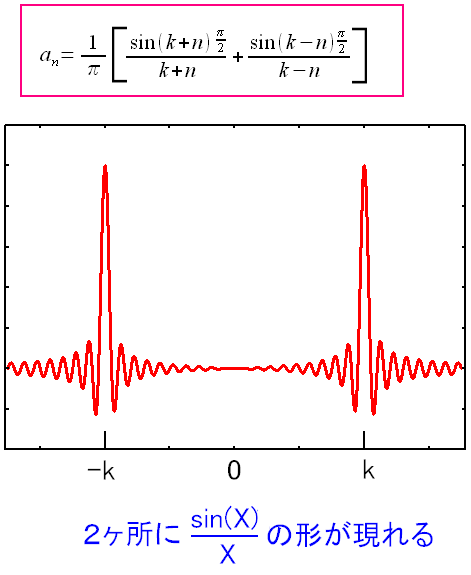 |
|
数学的には、このグラフになる。 だが、物理や工学では、実在しない部分は切り捨てる。 「k > 0」で、かつ「n > 0」なので、グラフの左半分は 無視しても良いのだ。 |
フーリエ展開で求めた式を使って、ASK変調のグラフができるかどうか 確かめる事にした。
| フーリエ展開で求めたASK変調の式をグラフで見てみる |
|---|
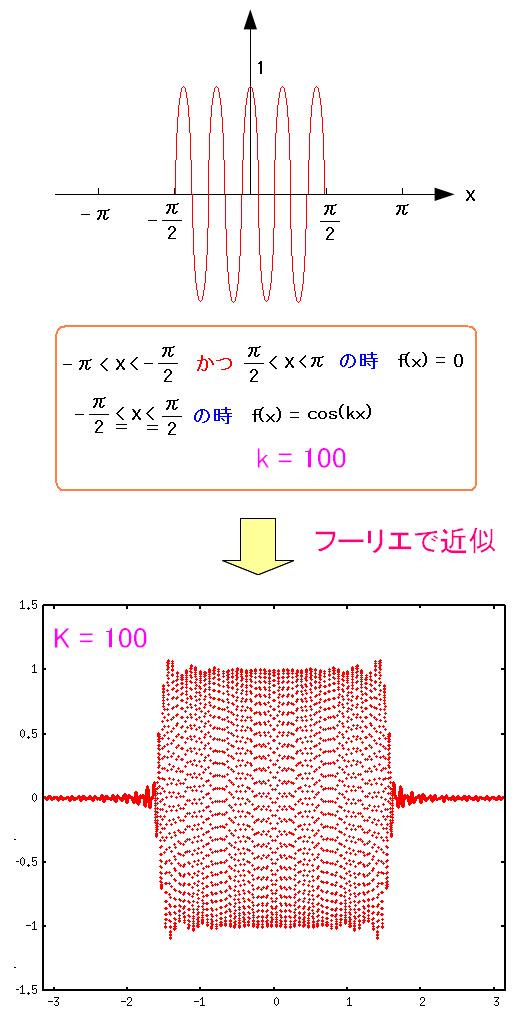 |
| nの値は80〜120の値にしています。 |
綺麗にできてるやん!
そして細部について見る事にした。
| フーリエ展開で求めたASK変調の式をグラフの細部 |
|---|
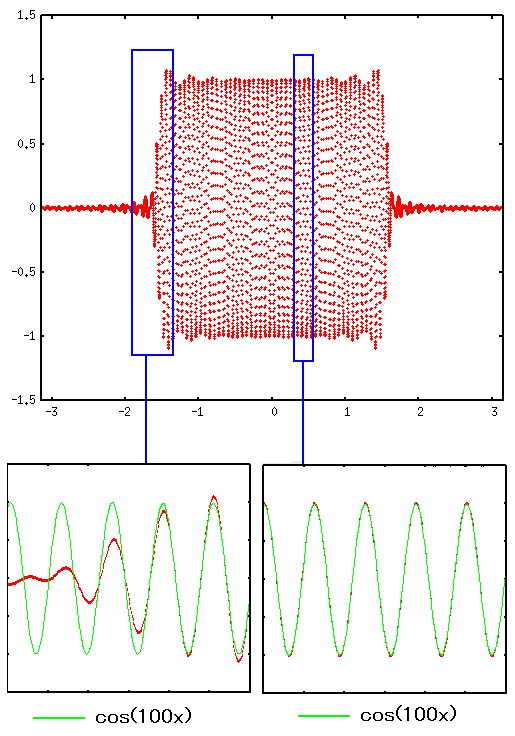 |
| 見事な近似としか言いようがない |
思わず 素晴らしい!! と思った。PSK変調 フーリエ展開とスペクトラム分布
次にPSK変調のフーリエ展開を考えてみる。
| PSK変調 |
|---|
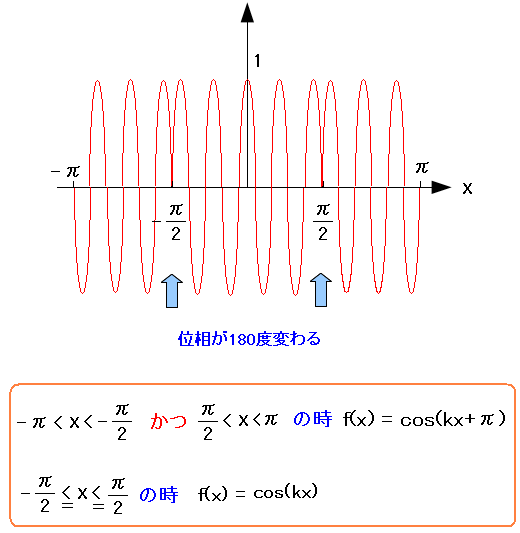 |
|
PSK変調は位相を180度ズラす事で「0」「1」を区別している。 そこで「1」の場合は、上図のような形にして考える事にした。 |
フーリエ展開を行なうのだが、計算量を減らすために偶関数にしておく。
| PSK変調とフーリエ展開 |
|---|
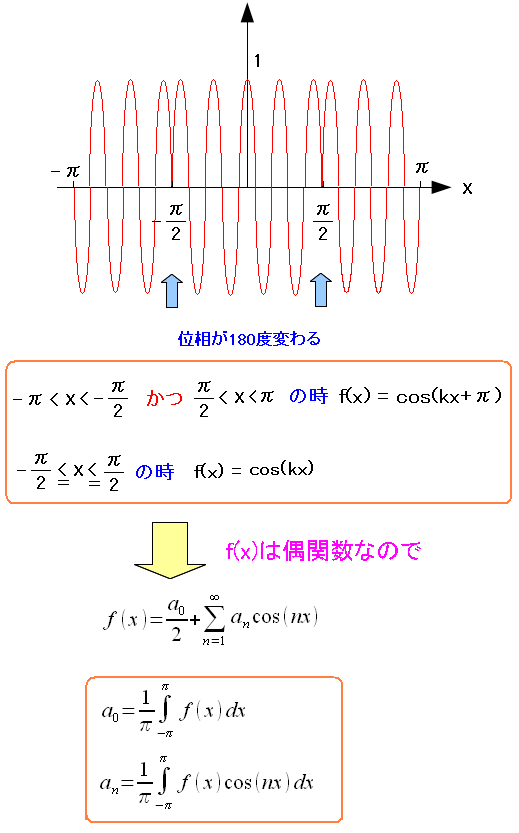 |
|
最初からPSK変調の関数を偶関数にしてしまえば フーリエ展開の際、偶関数の部分だけ計算すれば良いのだ。 |
まずはフーリエ係数の計算から
| フーリエ係数の計算 |
|---|
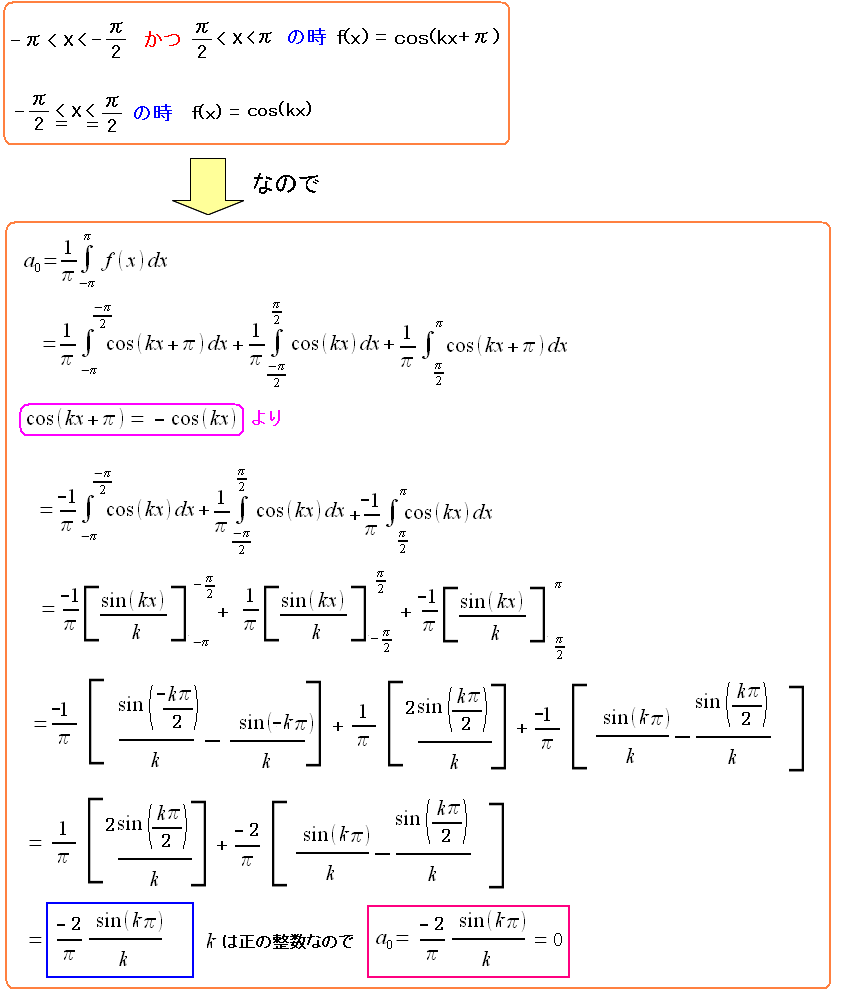 |
次にフーリエ余弦係数を求める。
| フーリエ余弦係数の計算 |
|---|
 |
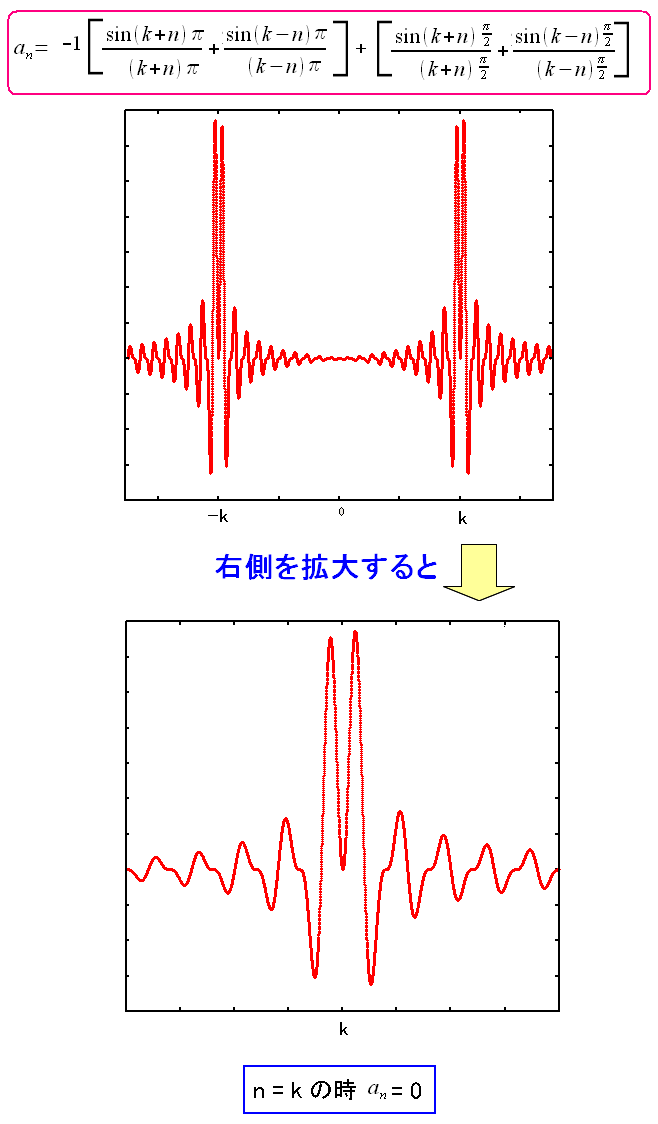
スペクトラム分布を見てみる。 フーリエ余弦係数の分布図なのだ。
| スペクトラム分布 |
|---|
 |
|
数学的には左右対象の山ができる。 だが、現実に起こりえない事象は、物理や工学では切り捨てる。 「n > 0」かつ「k > 0」なので、右側の部分のみ着目する。 |
直接拡散方式 (DSSS変調)の仕組み
2次変調に使われる直接拡散方式(DSSS)がある。 DSSSとは Direct Sequence Spread Spectrum の略で、日本語に訳すと「直接拡散スペクトラム」なのだ。 直接拡散方式とは、前の方で簡単に説明したが 一定の枠内にある周波数帯域を、広げて、平べったくする事だ。
| 直接拡散方式 DSSS |
|---|
 |
|
平べったい感じの信号になる。 まるで拡散した感じなので、直接拡散方式というようだ。 |
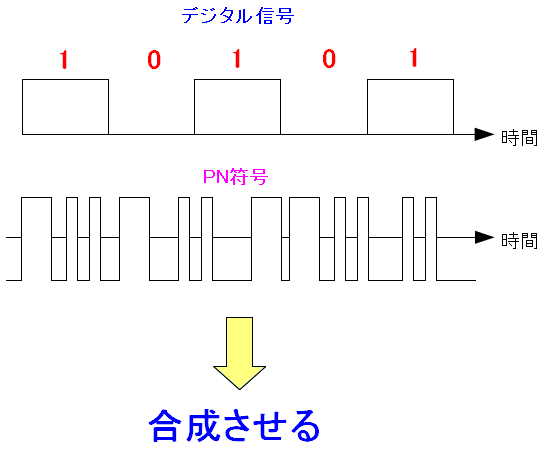
ここで思った。 実際に直接拡散の様子を見てみたい! そこで直接拡散の方法を調べてみた。 すると PN符号を使う 事がわかった。 PN符号とは・・・ Pseudo Noise (疑似雑音) という意味だ。 ところで、PN符号をどうやって使うのか。
| PN符号の使いかた |
|---|
 |
|
デジタル信号の周波よりも短いパルスを使う。 デジタル信号と短いパルス波の合成を行なう。 |
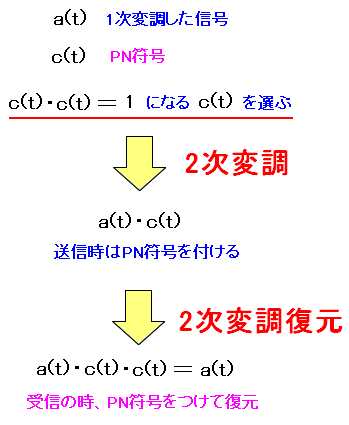
ところでPN符号を使って、どうやって直接拡散方式の変調を行なったり 復調するのか。 原理を調べたら、概略は以下のようになる。
| 直接拡散方式での変調と復元の考え方 |
|---|
 |
|
PN符号をc(t)をする。 この時、c(t)の2乗は「1」になるc(t)を考える。 変調を行なう際は、1次変調の信号a(t)にc(t)をかけ合わせる。 これで直接拡散の変調ができあがり。 そして復調する時は、a(t)c(t)にc(t)を掛け合わせると 元のa(t)信号に戻る。 |
無線の送受信の図を使って見てみる。
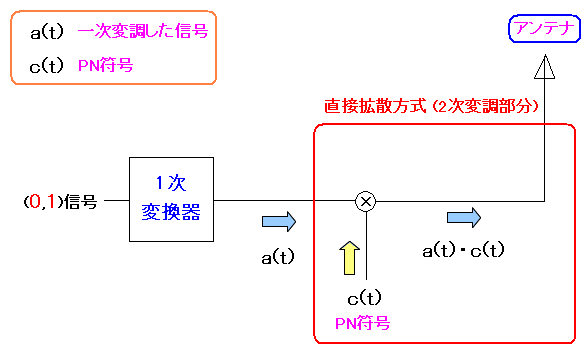
| 直接拡散方式の送信側 |
|---|
 |
|
一次変調した信号a(t)に、PN符号のc(t)を掛け合わせる。 それを電波として送信する。 |
受信側は以下のようになっている。
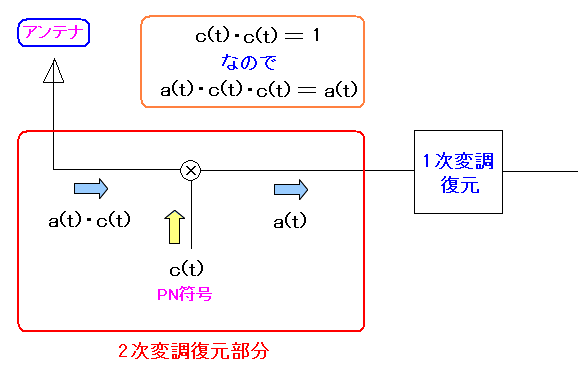
| 直接拡散方式の受信側 |
|---|
 |
|
受信した信号にPN符号のc(t)を掛け合わせて 元の1次変調後の信号a(t)に復元するのだ。 |
もちろん、電波は空間を飛んでいる間に様々な電磁波の影響を受ける。 それが妨害波(雑音・ノイズ)なのだ。 ところで直接拡散方式は妨害波(雑音・ノイズ)に強いと言われる。 その理由を以下の図で説明してみた。
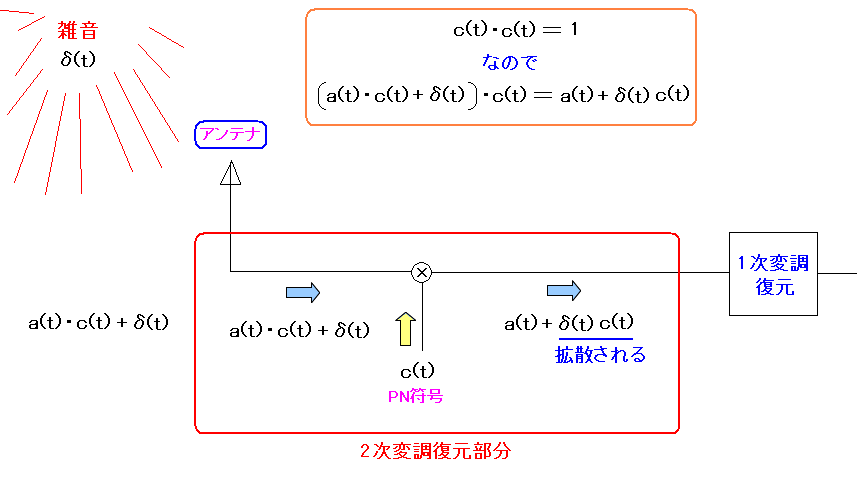
| 直接拡散方式が妨害波(雑音・ノイズ)に強い理由 |
|---|
 |
|
妨害波をσ(t)とする。 受信した信号はa(t)・c(t)+σ(t)となる。 だが、復調時にPN符号を掛け合わせるとa(t)+σ(t)・c(t)となり 妨害波(雑音・ノイズ)が拡散され、元の信号が取り出しやすくなるのだ。 |
ASK変調と直接拡散方式
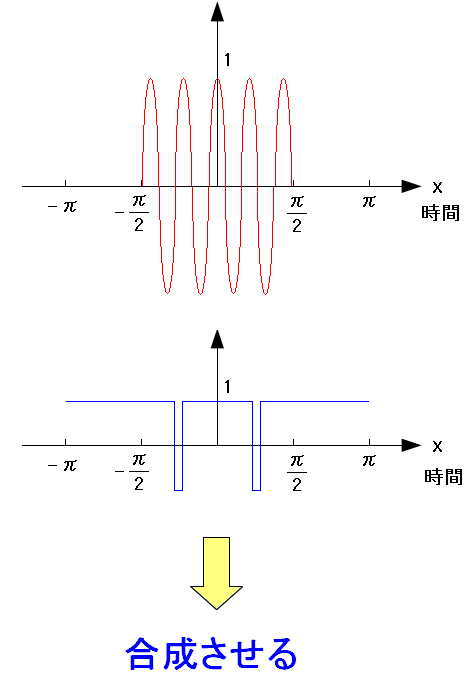
直接拡散方式の概略がわかった所で、ASK変調したデジタル信号を 直接拡散方式で変調する場合を考える。
| ASK変調とPN符号 |
|---|
 |
|
上図のように、合成しても偶関数の形にするようにした。 計算量を減らすためだ。これを横着というのだ。 |
PN符号は「-1」と「1」の信号だ。
| PN符号とチップ区間 |
|---|
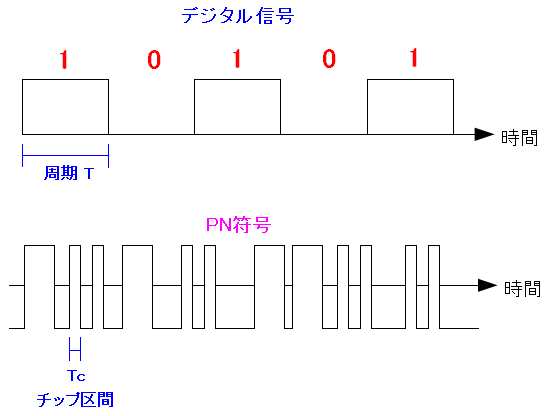 |
| PN符号の最小の信号幅を「チップ区間」という。 |
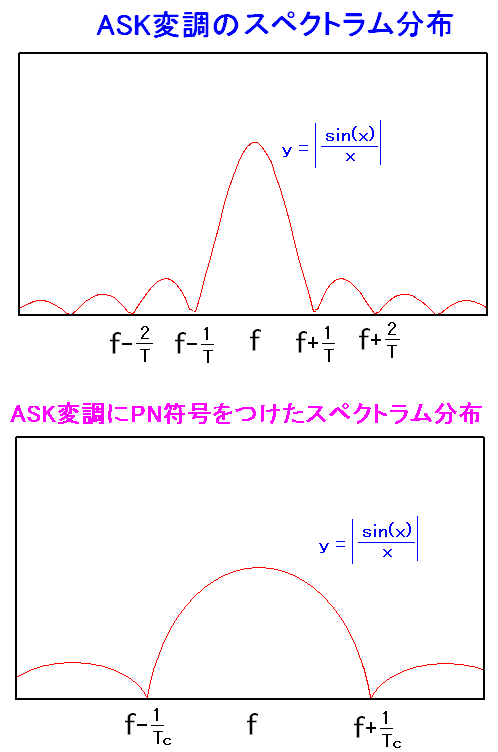
PN符号を掛け合わせる事で、ASK変調のスペクトラム分布に 変化が起こるという。
| スペクトラム分布の変化 |
|---|
 |
|
ASK変調の場合、スペクトラムの広がりは周期に依存する。 PN符号を使った場合は、スペクトラムの広がりはチップ区間に 依存するというのだ。 |
これを自分の目で確かめる事にした。
| ASK変調とPN符号 |
|---|
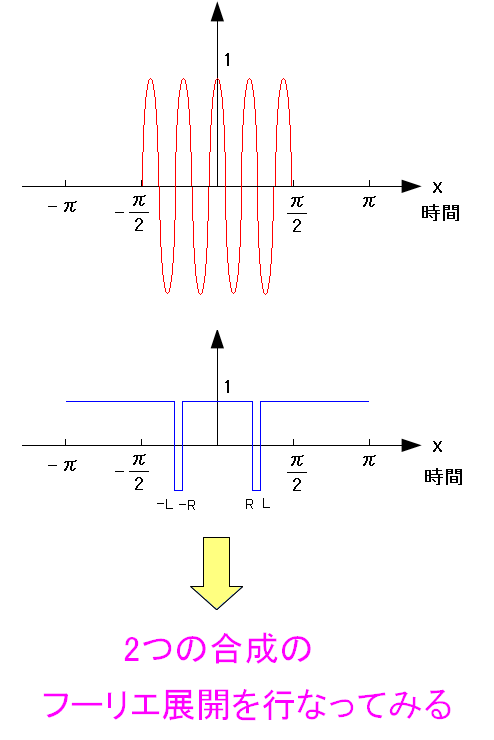 |
| 簡単なモデルでのASK変調とPN符号をつける事にした。 |
そしてフーリエ係数を算出する。
| フーリエ係数を算出 |
|---|
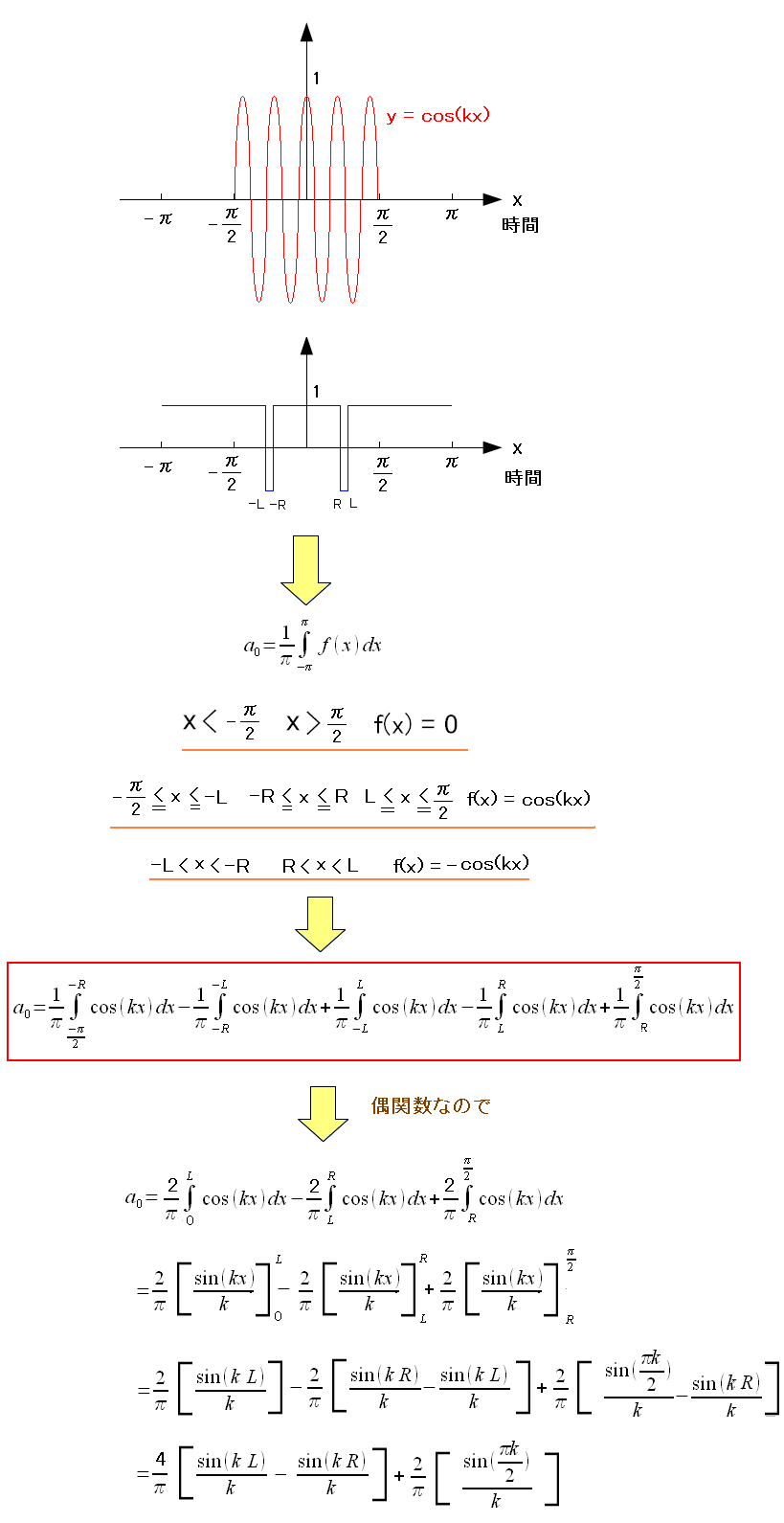 |
そしてフーリエ余弦係数を算出する。
| フーリエ余弦係数を算出 |
|---|
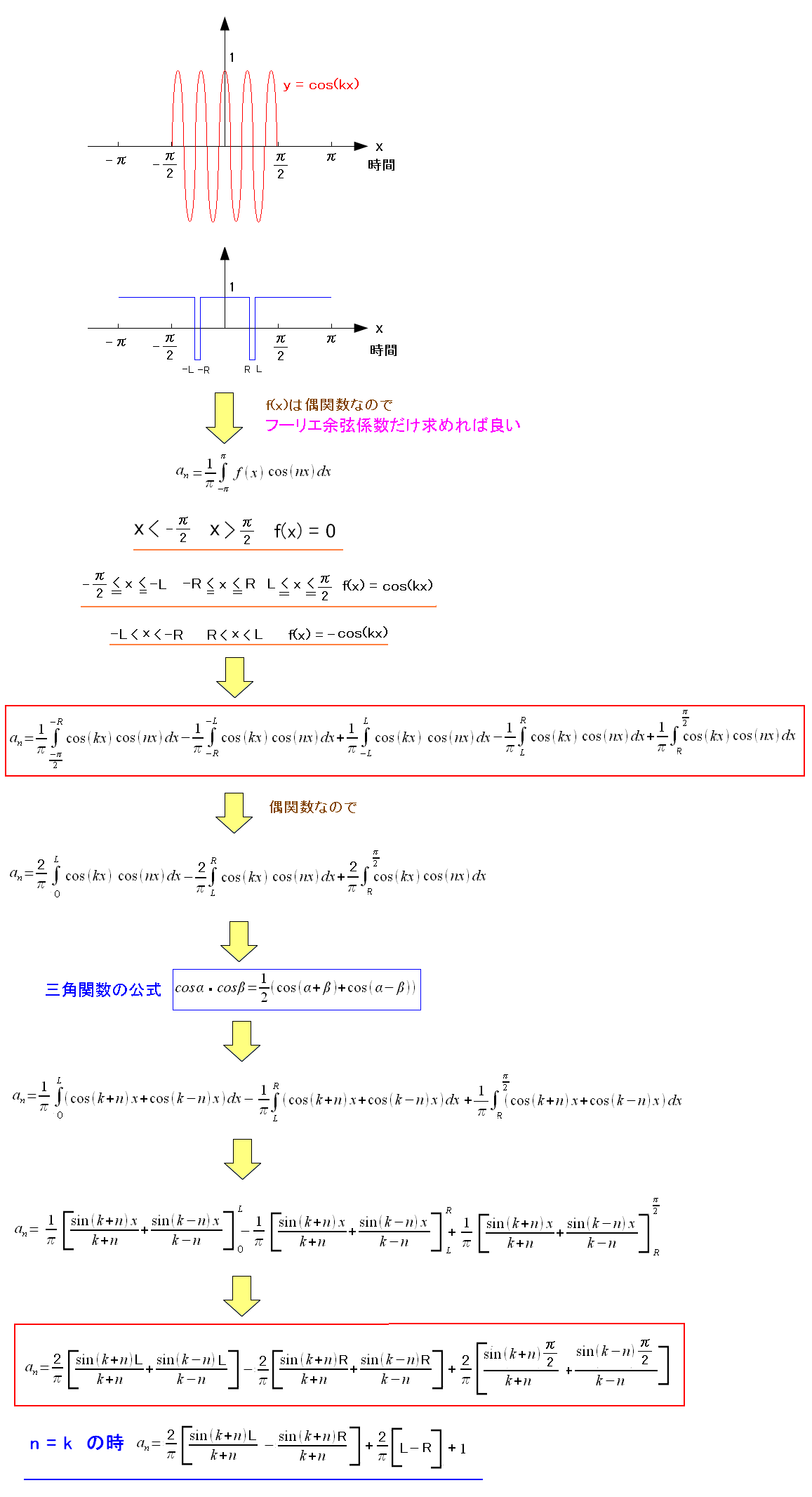 |
求まったフーリエ級数を使ってグラフに描いてみた。
| 求まったフーリエ級数を使って描いたグラフ |
|---|
 |
|
[-L,-R」と[R,L]間はPN符号で「-1」になっている部分だ。 その部分が、くびれた感じになっている。 |
[R,L]間を拡大してみる。
| [R,L]間を拡大 |
|---|
![ASK変調 [R,L]間を拡大](pic104/ddds12.gif) |
|
[L,R]間は位相が、180度ずれている。 そのためフーリエ級数の計算が正しくできている事がわかる。 |
肝心のスペクトラム分布を見てみる。
| スペクトラム分布の比較 |
|---|
 |
|
赤いのがASK変調のスペクトラム。 緑が、簡易的なPN符号をつけてみた場合のスペクラム分布。 緑が平べったくなった感じがしない。 |
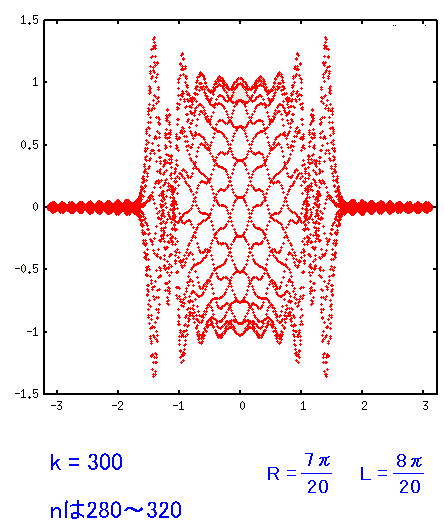
一体、どういう事やねん!! と思った。 調べてみると、スペクトラムが平べったくなるには PN符号の生成に工夫がいるというのだ。PN符号 M系列
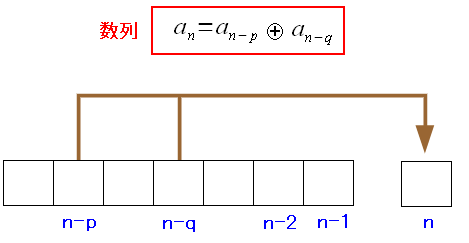
1次変調した信号を、綺麗な平べったいスペクトラム分布にするには 「1」と「-1」に偏りがない事 と 特定のパターンを繰り返さない事 といった条件がある。 ネットや本などを見てみると、そんな条件を満たす PN符号の生成方法に M系列、Gold系列 といった物があるという。 あるサイトのM系列の説明を見たら数式が多かったので 誰がそこまで勉強するか! と思った。 だが、食わず嫌いしても仕方ない上、そんな事を許してくれる 読者ばかりではない。 そんな中、ふと、本を見た。 M系列の原理は簡単やん!
| M系列のPN符号生成の仕組み |
|---|
 |
|
数列と考えれば、見通しが良くなる。 任意の数列を用意する。この場合だと7ビットになる。 8ビット目からは、初期値の数列の排他的論理和の値を使う。 |
M系列方式では、実際に、どうやってPN符号の算出をしているのか。 それを見てみる事にした。
| M系列のPN符号の値の算出法 |
|---|
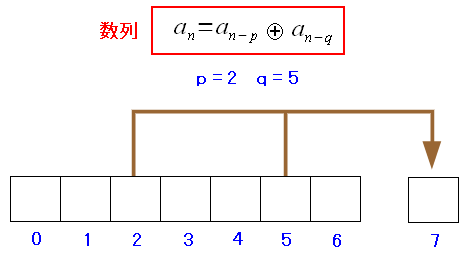 |
|
7個の数列を用意する。 「0」か「1」だけなので7ビットで表現できる。 pとqの値は任意に決められる。 |
具体的に数列に初期値の値をいれてみる事で、8ビット目の値を求めてみる。
| M系列のPN符号の値の算出 |
|---|
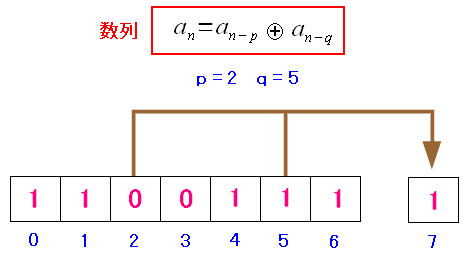 |
|
上図のように、7ビットの中の2つの数列の値の排他的論理和を 8番めのビットの値にする。この場合は「1」になる。 |
そして数列の値を次々と求めていくと、次のようになる。
| 数列の値を次々と求めていく |
|---|
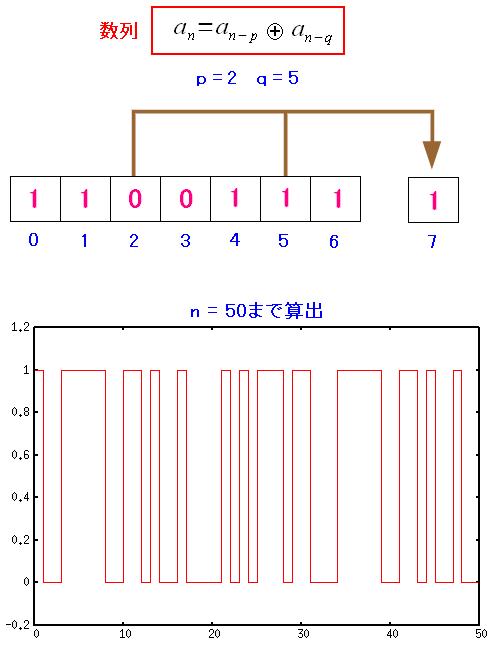 |
|
50番目の値まで求めてみた。 それをグラフ化してみた。 勘の良い方なら「周期がありそう」と思われるだろう。 私は、この時点では気づかなかった。 周期性の話については後述しています。 |
でも、このままではPN符号として使えない。 PN符号は、2乗すると「1」になる必要があるからだ。
| 求まった数列と、実際のPN符号の関連付け |
|---|
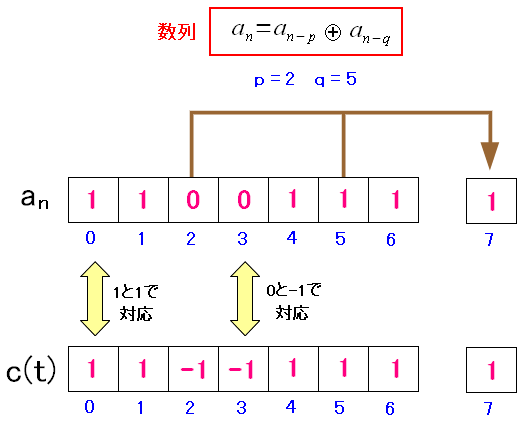 |
|
数列と、PN符号として使う関数との関連づけだ。 これだと c(t)・c(t)=1 になるのだ。 |
ASK変調とPN符号(M系列)で直接拡散方式とスペクトラム分布
早速、M系列で生成するPN符号を使って、ASK変調の直接拡散と スペクトラム分布を見てみる事にした。
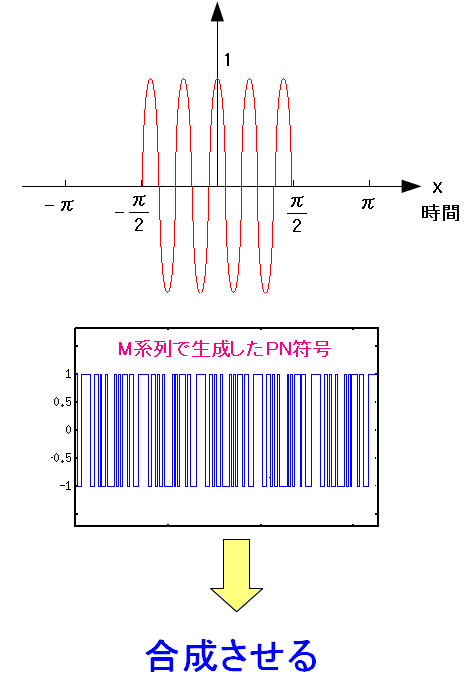
| ASK変調とM系列で生成したPN符号 |
|---|
 |
|
PN符号がY軸において左右対称でないため、合成した物が 偶関数でなくなる。そのため計算量が増えるのだ。 |
どんなフーリエ係数になるのか。 算出方法を書いてみた。
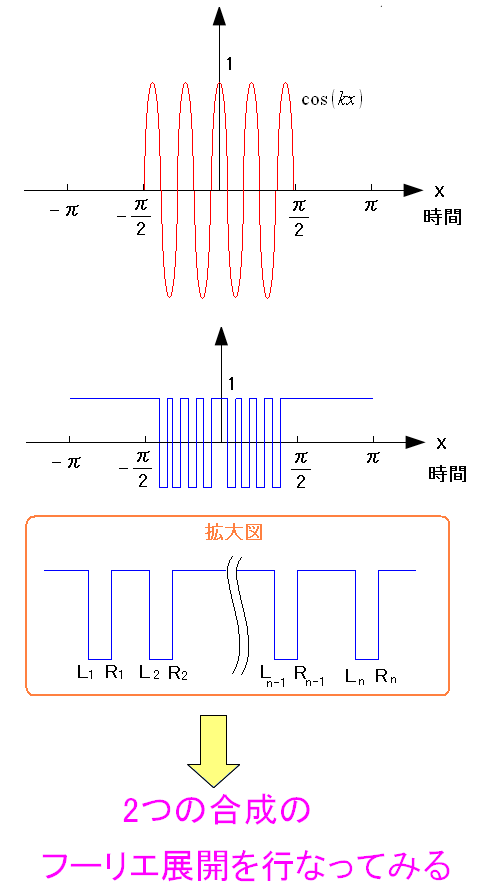
| フーリエ級数の計算方法 |
|---|
 |
|
PN符号で「-1」になるのが、n個ある場合を考える。 n個な上、左右対象でなくなるので、偶関数の扱いはできなくなる。 |
まずはフーリエ係数を求めてみる事にした。
| フーリエ係数の計算方法 |
|---|
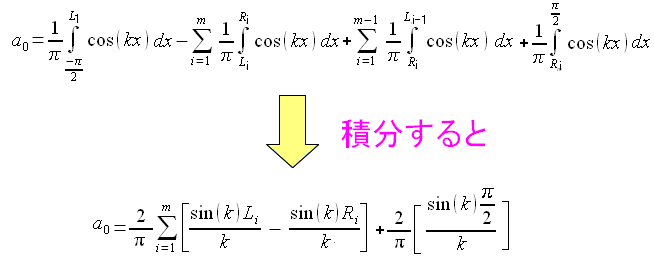 |
| 案外、すっきりした形になった。 |
次にフーリエ余弦係数を求める事にした。
| フーリエ余弦係数の計算方法 |
|---|
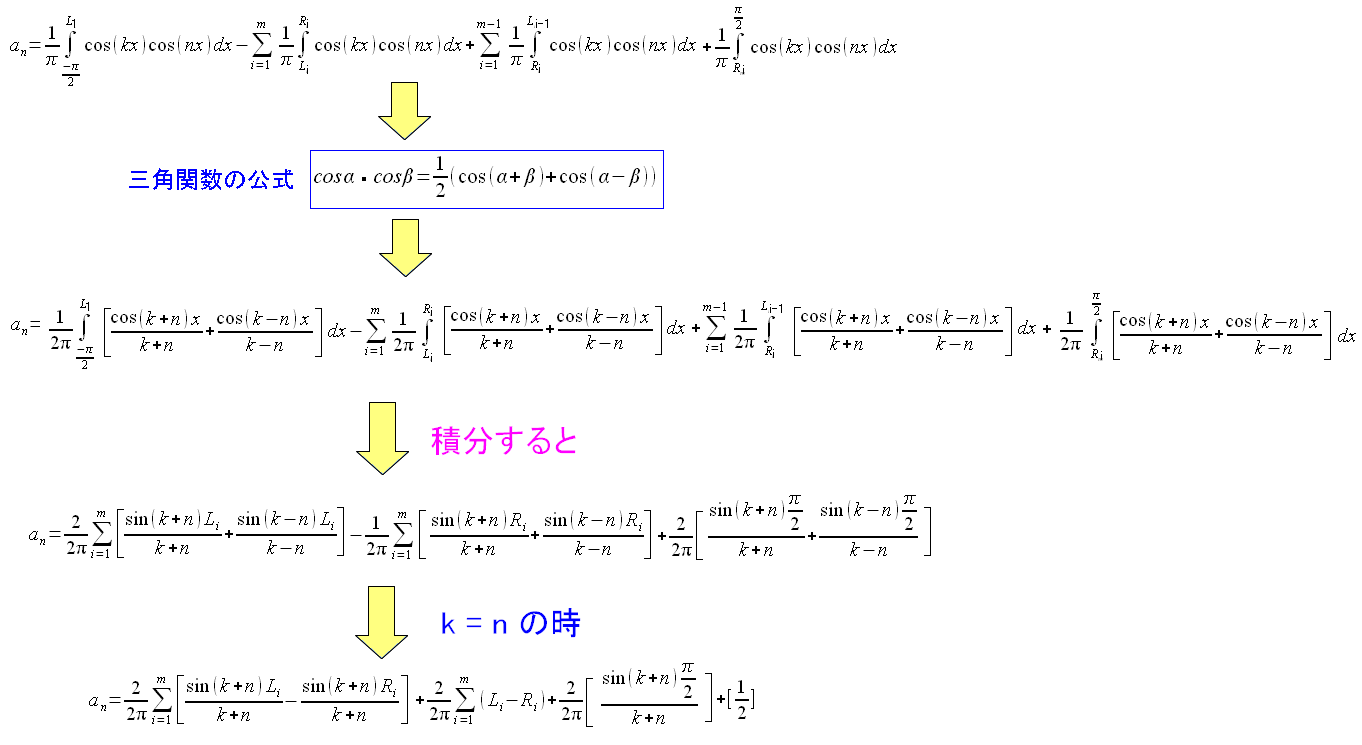 |
|
「k=n」の場合を求めたのは、数値計算の際 「0÷0」の形にならないようにするためだ。 |
そしてフーリエ正弦係数を求めてみる。
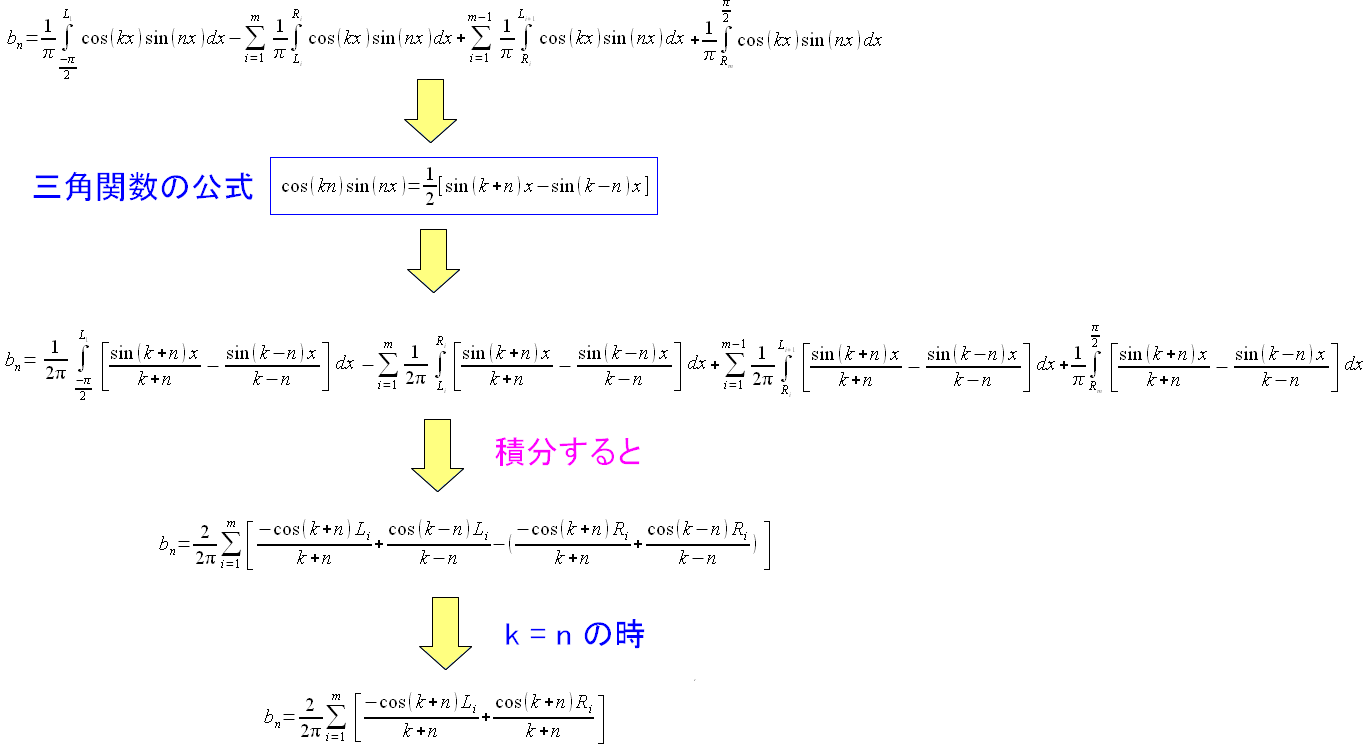
| フーリエ正弦係数の計算方法フーリエ正弦係数の計算方法 |
|---|
 |
|
ここでも「k=n」の場合を求めたのは、数値計算の際 「0÷0」の形にならないようにするためだ。 |
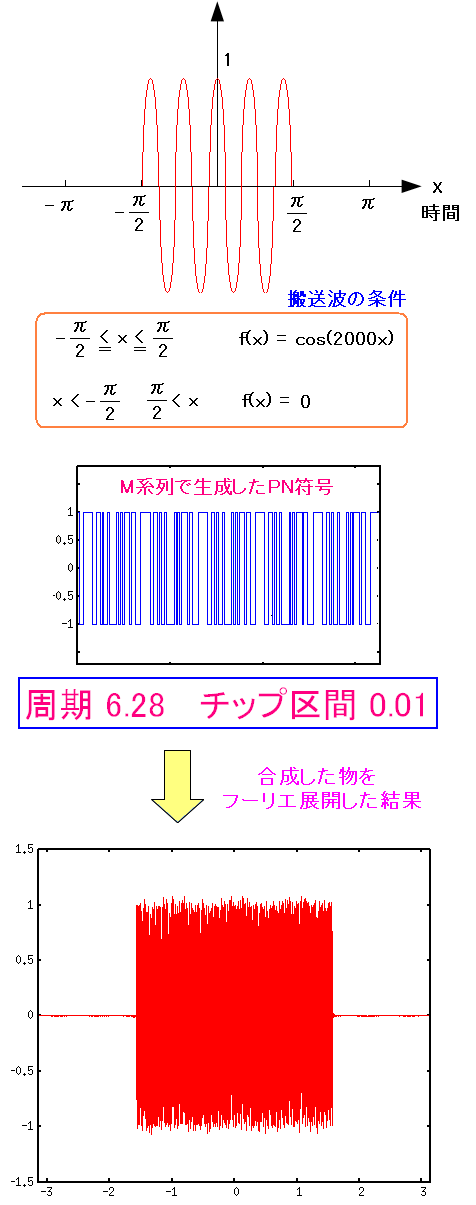
そして、ASK変調の信号をPN符号を掛け合わせ それで求まったフーリエ展開を使って、グラフに表す。
| ASK変調をPN符号を掛け合わせた物を フーリエ展開しグラフにする |
|---|
 |
|
-3.14〜3.14の区間を1周期とする。 PN符号のチップ区間を0.01にする。 理論上、スペクトルの広がりが628倍になるのだ。 |
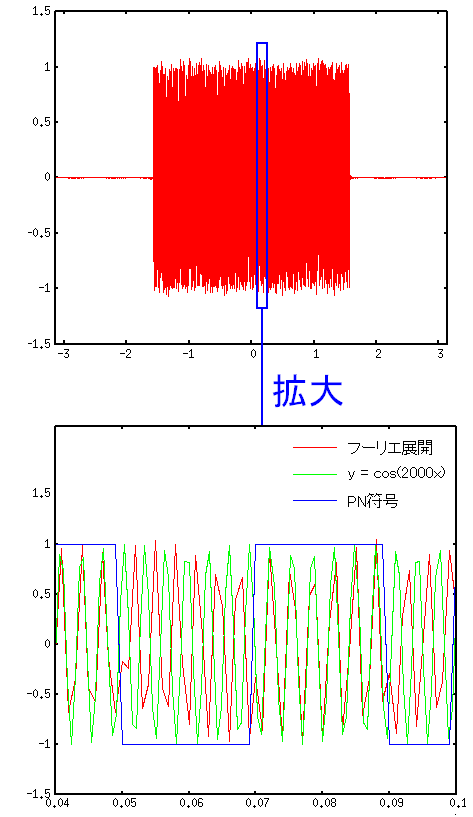
実際にフーリエ展開で、表現できているかどうか確認してみた。
| 実際にフーリエ展開で、表現できているかどうか確認 |
|---|
 |
|
赤い線がASK変調にPN符号をつけた物。 緑の線は、搬送波のcos(2000x)の線。 青がPN符号の値だ。 PN符号が「1」の時、ASK変調の位相と 搬送波のcos(2000x)の位相が一致している。 「-1」の時、位相が180度ずれている。 |
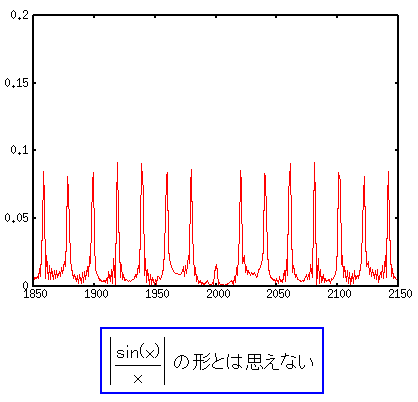
スペクトラム分布を見てみる
| ASK変調にPN符号をつけたスペクトラム分布 |
|---|
 |
|
スペクトラム拡散している感じはないし sin(x)/xの形状をしているようにも思えない。 |
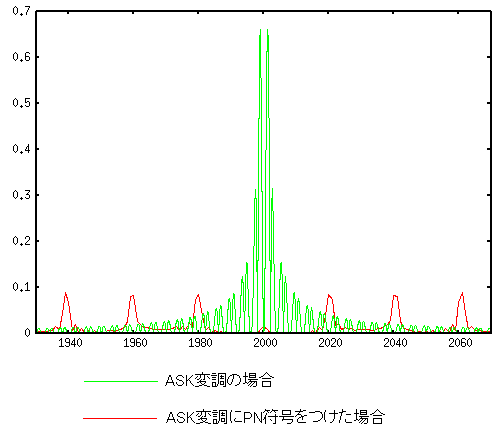
ASK変調のスペクトラム分布と比較してみた。
| スペクトラム分布 |
|---|
 |
|
ASK変調は緑の線で、搬送波の周期(2000)を中心の山になっている。 赤い部分は、PN符号をつけた場合。直接拡散方式の変調後になる。 スペクトラム分布が拡散しているように思えるのだが これだけだと、よくわからん。 |
そして、本などの説明と一致しない。
| 本などで説明されている 直接拡散方式によるスペクトラム分布 |
|---|
 |
|
本の説明では、山が、直接拡散方式(DSSS)によって 平べったい形になっていると説明されている。 |
だが、私が算出したグラフでは・・・
平べったい形になってへん!!
散々、悩んだ上、途中、計算間違いなどもあって七転八転した末
グラフの範囲を広げてみる事を思いついた。
| ASK変調にPN符号をつけた物のスペクトラム分布(2) |
|---|
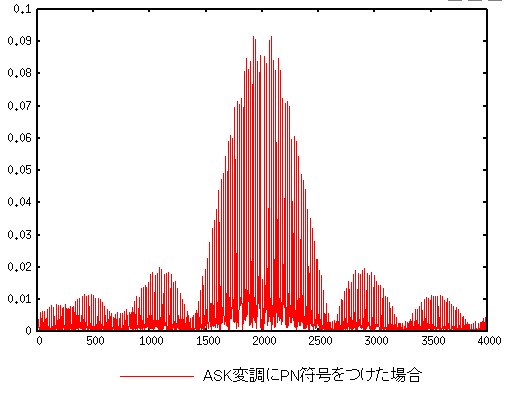 |
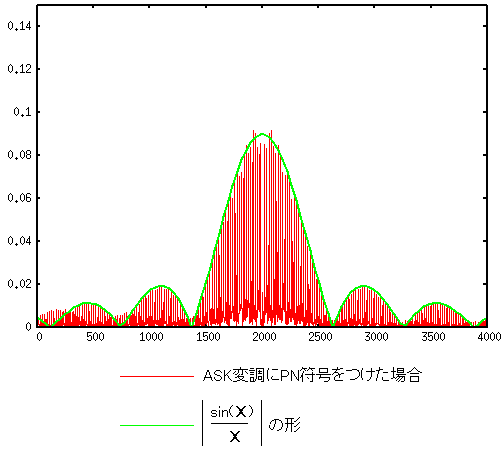
ふと気づいた。
スペクトラム分布の輪郭だ
| スペクトラム分布と、その輪郭 |
|---|
 |
|
輪郭を見ると、sin(x)/xの形状になっている。 本などの説明にあるスペクトラム分布が平べったい形になるのは スペクトラム分布のグラフそのものではなく 輪郭の事を意味するのがわかった。 |
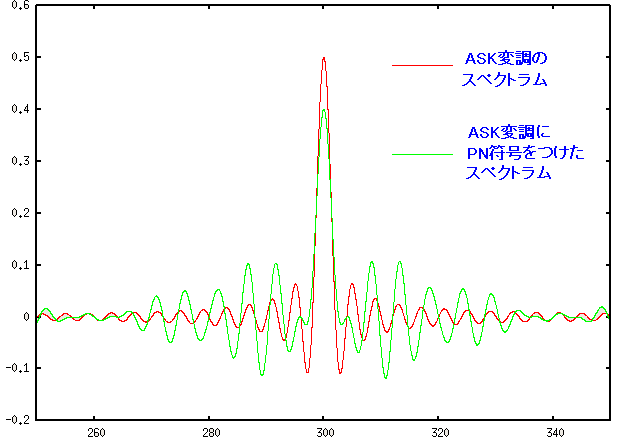
これに気づくのに結構時間がかかった。 ASK変調のスペクトラムと、PN符号をつけた直接拡散変調後の スペクトラムの比較を行なってみた。
| スペクトラム分布の比較 |
|---|
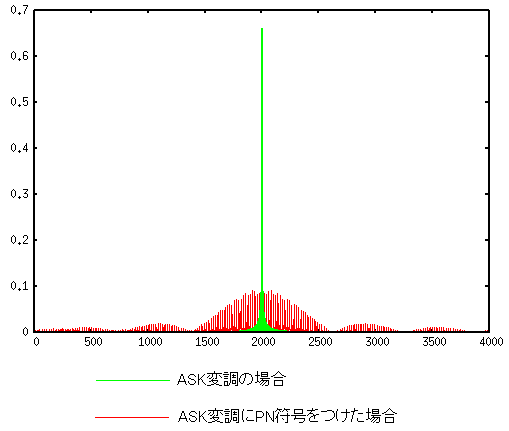 |
|
PN符号をつける(直接拡散変調)する事によって スペクトラム分布が広がっているのがわかる。 |
実際、どれくら広がっているのか確かめてみる。
| スペクトラム分布の拡大率 |
|---|
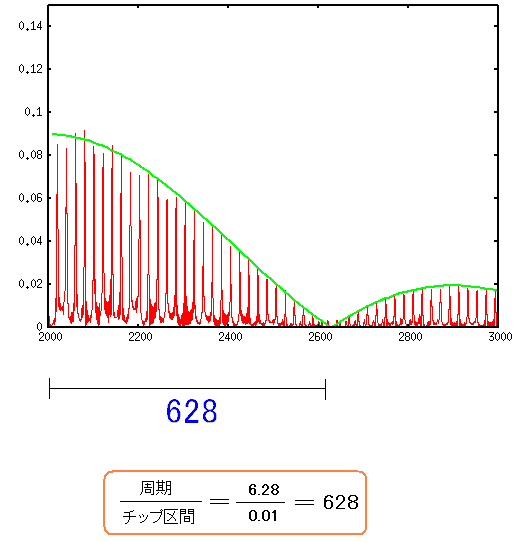 |
| 見事に計算式と一致している |
PSK変調とPN符号(M系列)で直接拡散方式とスペクトラム分布
次に、M系列で生成するPN符号を使って、PSK変調の直接拡散と スペクトラム分布を見てみる事にした。
| PSK変調にPN符号を付け、フーリエ展開し それをグラフ化 |
|---|
 |
まずは[-π/2,π/2]を拡大して見てみる
| [-π/2,π/2]を拡大 |
|---|
![PSK変調にPN符号をつけてフーリエ展開した物 それを[-π/2,π/2]を拡大](pic104/ddds25.gif) |
|
PN符号が「1」の場合、緑の搬送波と赤のフーリエ展開した物が同じ位相で PN符号が「-1」の場合、位相が180度ずれている。 フーリエ展開が、キチンとできている事がわかる。 |
見る範囲を[π/2,π]にしてみる。
| [π/2,π]を拡大 |
|---|
![PSK変調にPN符号をつけてフーリエ展開した物 それを[π/2,π]を拡大](pic104/ddds26.gif) |
|
PN符号が「1」の場合、緑の搬送波と赤のフーリエ展開した物が 位相が180度ずれている PN符号が「-1」の場合、位相が同じになっている。 フーリエ展開が、キチンとできている事がわかる。 |
そしてフーリエ係数の分布であるスペクトラム分布を見てみる。
| PSK変調にPN符号をつけた場合の スペクトラム分布 |
|---|
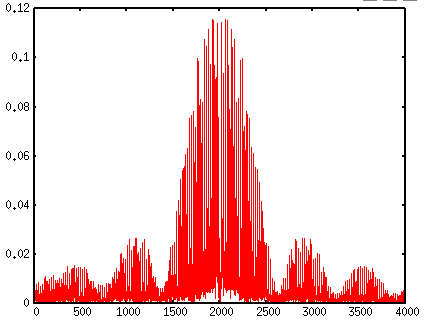 |
|
これだけだと、最初のPSK変調のスペクトラム分布から PN符号を付けて、直接拡散した後のスペクトラム分布が どれくらい広がったのか、わからない。 |
そこでスペクトラム分布の比較を行なった。
| PSK変調と、PSK変調にPN符号をつけた物(直接拡散)との スペクトラム分布の比較 |
|---|
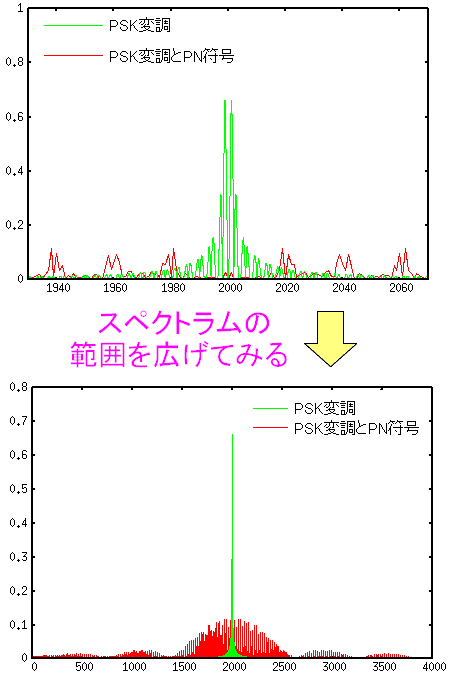 |
|
PN符号を付ける(直接拡散)をする事で、スペクトラム分布が 広がっているのが一目瞭然だ。 |
直接拡散方式での同期の取り方
PN符号について調べていくと、送信側と受信側の 同期の取り方の話が出てきた。 PN符号の特徴を利用して、同期を取るという。
| PN符号の信号 (M系列) |
|---|
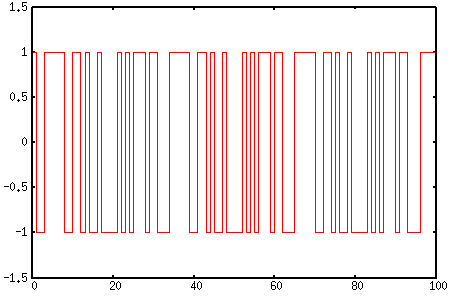 |
これを良くみると
| PN符号の信号に周期性がある |
|---|
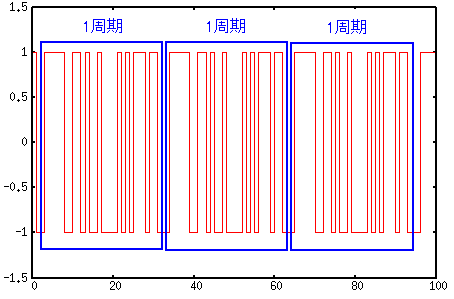 |
| PN符号には周期性がある事がわかる。 |
そのためPN符号の周期性を利用して送信側と受信側は 同期を取っているのだ。
| PN符号の周期性を利用した同期の取り方 |
|---|
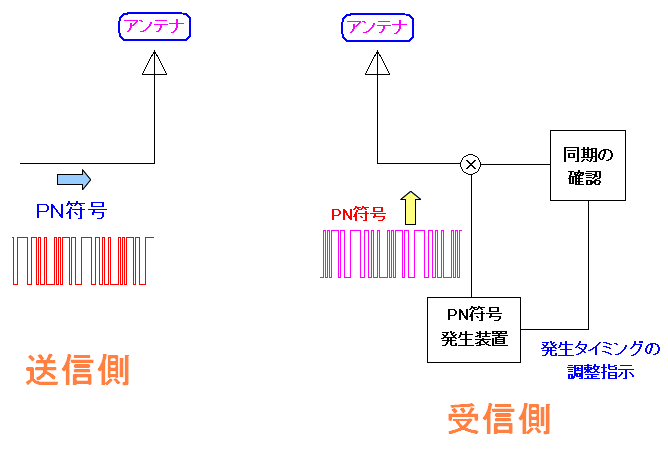 |
|
送信側がPN符号を送る。 受信側が送られて来たPN符号と、自分の所で発生させたPN符号を比較する。 もし、一致しない場合は、発生タイミングを遅らせる指示を出して 一致するまで繰り返す。 |
自己相関関数
さて、PN符号は、自己相関関数と言われる。 ところで・・・ 自己相関関数とは何やん? なのだ。 そこで調べてみる事にした。 すると・・・ 関数自身の高い周期性を調べる関数 なのだ。 自己相関関数とは、どんな関数なのか見てみる事にした。
| 自己相関関数 |
|---|
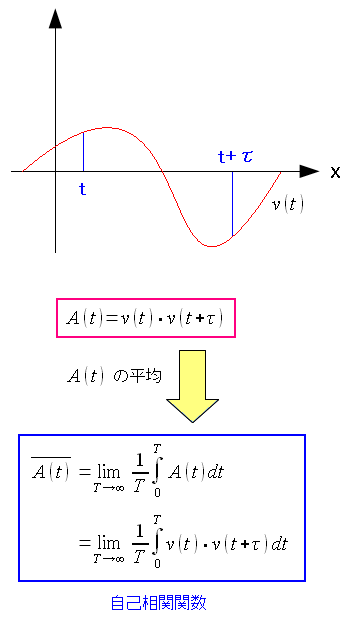 |
|
ある時間関数v(t)がある。 自己相関関数とは、時間tの時点のv(t)と、 tからτ離れたv(t+τ)との積を全時間で割った物だ。 |
だが、これだけだと
どんな関数なのか、わからへん!
なのだ。
もう少し詳しく見る事にした。
| 自己相関関数の定義式 |
|---|
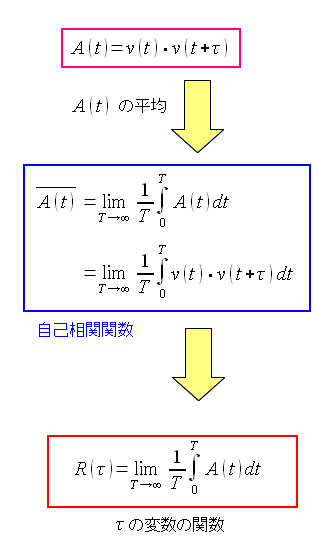 |
|
τの値で変動する、τの関数だというのは、わかる。 v(t)・v(t+τ)の値の変動を見る上、時間積分するため τの関数になるのだ。 |
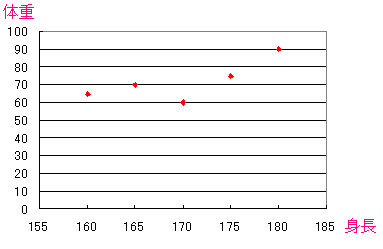
だが、いくら式を眺めても・・・ 意味が理解できへん!! だった。 色々、ネットで調べたりしたのだが、納得できる物が見つからない。 このままでは前に進まないので・・・ 自己相関関数なんて、わかるわけねぇ! と開き直り、さっさと終わらせようと考えた。 そんな矢先、以下の本を書店で発見した。 「統計学の基礎のキ 分散と相関係数編」(石村貞夫、石村光資郎:東京図書) これを読み進めていくと・・・ 目からウロコ だった。 まずは本に書いている相関関係の部分を読んでみた。 相関関係、よくあるのが身長と体重の相関関係だ。 背が高い人は体重が重いという関係は成り立つのか 以下の表を作成してみた。
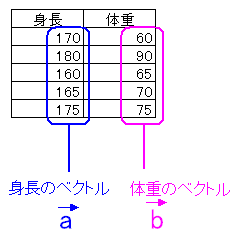
| 身長と体重 | ||
|---|---|---|
| 名前 | 身長(cm) | 体重(Kg) |
| A | 170 | 60 |
| B | 180 | 90 |
| C | 160 | 65 |
| D | 165 | 70 |
| E | 175 | 75 |
これを分布図で表すと以下のようになる。
| 5人の身長と体重の分布図 |
|---|
 |
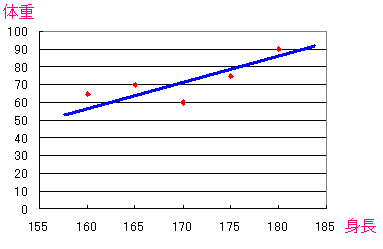
上の分布図に、点の間を通る線を引いてみる。
| 身長と体重の分布図 |
|---|
 |
|
線を引くと、身長と体重の間には法則性があるようだ。 相関性があるようだ。 |
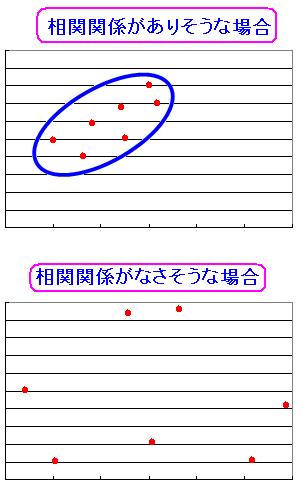
視覚的みると、相関関係がありそうな分布図と 相関関係がなさそうな分布図が
| 相関関係の有無について |
|---|
 |
|
1つの集団にまとまっているのが相関性がありそうに見える。 バラバラなのが、相関性がなさそうに見える。 |
視覚的に相関関係を見る事ができるが、本は、それだけで終わっていない。 どれくらいの相関性があるのか、数値化してみる方法が書いていた。
| 身長と体重をわけて考える |
|---|
 |
|
身長と体重の組み合わせではなく、身長と体重を別個に考える。 ここでは5個、成分があるので、5次元ベクトルとして考える。 |
身長、体重共に、ベクトルで考えてるのは、意外な感じがした。
| 身長・体重の値をベクトルでまとめる |
|---|
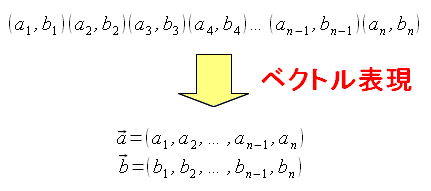 |
|
身長の、それぞれの成分を(a1,a2,a3,…,an)にし 体重の、それぞれの成分を(b1,b2,b3,…,bn)にする |
そして2つのベクトルの内積を考える。
| 2つのベクトルの内積を考える |
|---|
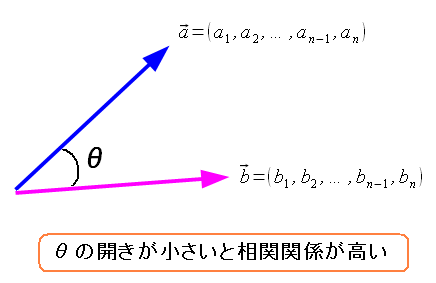 |
| ベクトルの内積とは、2つのベクトルの間の角度の大きさだ。 |
ここで気づいた。 もし、相関関係があれば どっちも似たような方向性を持つ cosΘの値が大きければ相関関係がある という事だ。 腑に落ちた。 統計の話で、ベクトルを使うとは予想していなかったが すっきりしたのだ。
| 内積を求めてみる |
|---|
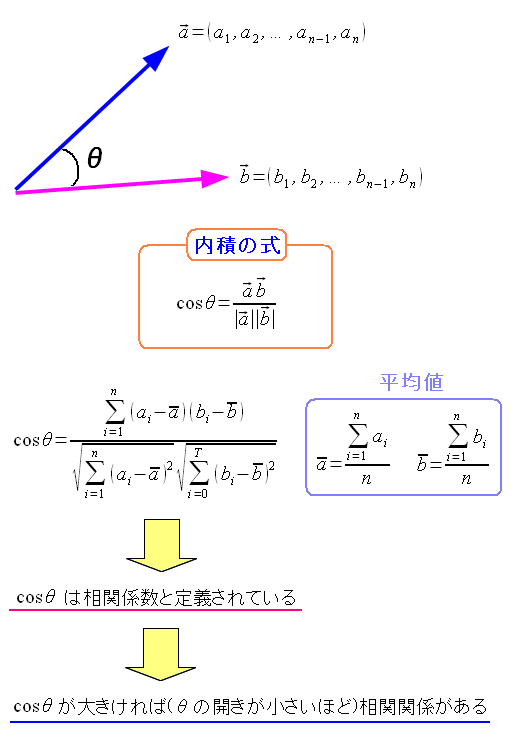 |
|
ベクトルと内積の式だ。 この時は知らなかったが、直交関数系も同じ考え方をしている。 「相関性がない=直交している=内積の値が0」なのだが それについては後述しています!! |
ベクトルの内積の式を見て、気がついた。
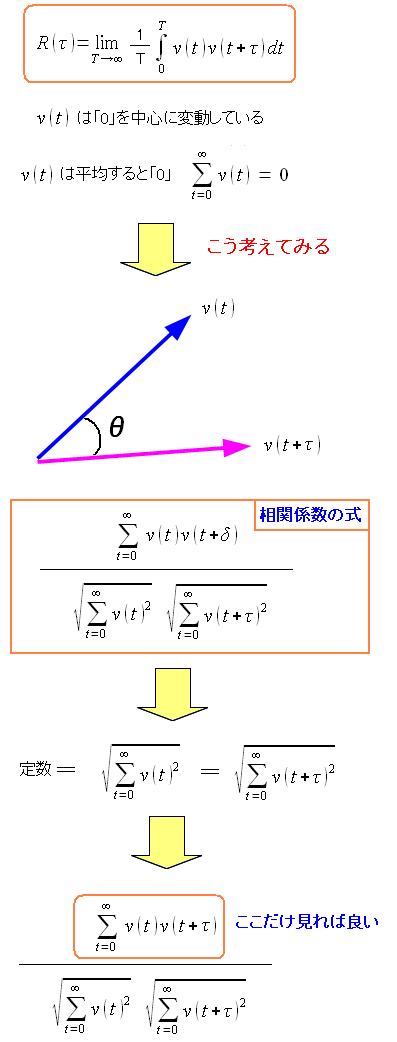
自己相関関数の式に似ているやん!
| 自己相関関数と相関係数とを照らし合わせて考えてみる |
|---|
 |
|
v(t)が周期性を持つかどうかを見るために v(t+τ)の値とを比較して、類似性があるかどうかを確かめる事だ。 |
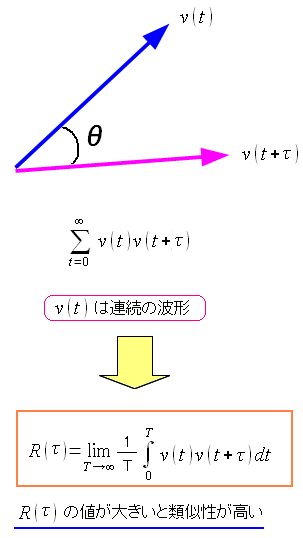
ところで自己相関関数は、連続関数の周期性を見るためなので 数列の和よりも積分を使った方が良い
| 自己相関関数 |
|---|
 |
|
R(τ)の値が大きければ、類似性がある、即ち、周期性が みらえると考えても良いのだ。 |
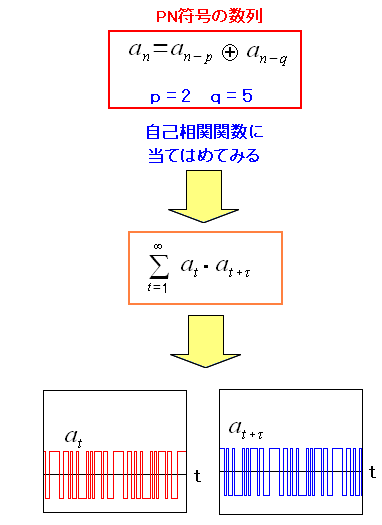
実際に、PN符号で作った物に当てはめて考えてみる PN符号は数列なので、積分ではなく、シグマ(数列の和)を使って 表現した方が良い。
| PN符号で作った物を当てはめて考えてみる |
|---|
 |
|
「τ」は、ズレの度合になる。 |
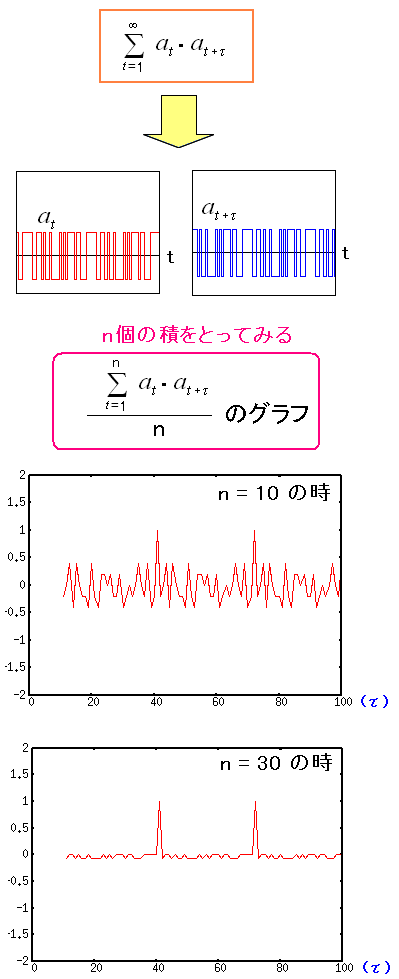
早速、計算してみる。
| PN符号の周期性に関する結果 |
|---|
 |
|
数列の数が少ない(10個)で見た場合よりも 数列の数が多い(30個)で見て方がわかりやすい。 |
ある程度、足し合わせる事で、類似性が高い値を検出しやすくなる。RAKE受信 マルチパス対策
ところで無線LANに限らず、無線通信の場合 マルチパス問題は避けられない。
| マルチパス問題とは |
|---|
 |
|
受信電波には、直接波と反射波がある。 反射波の場合、より長い距離を通っているため 遅れてやってくる。これを遅延波という。 |
マルチパスがあると以下の問題があるという。
| マルチパスによる干渉の問題 |
|---|
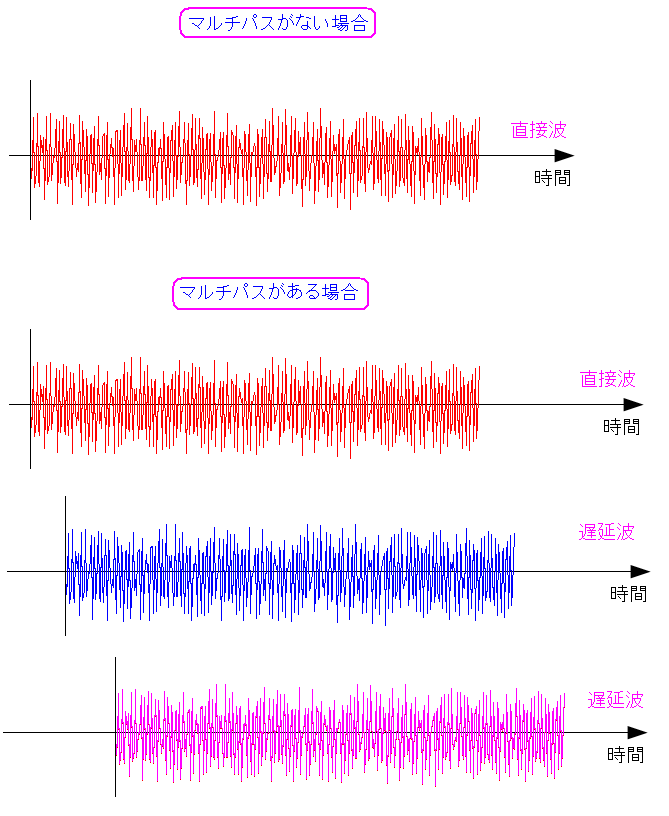 |
| 直接波と遅延波との間で干渉しあう問題が発生する。 |
そこで直接拡散方式では、RAKE受信という方法を使って マルチパス問題の解決を行なっている。 直接拡散方式の場合、搬送波とPN符号との同期がとれたら 搬送波から信号の復調でき、そうでなければ、拡散したままという性質がある。
| PN符号も同じだけ遅延させれば、遅延波を復調できる |
|---|
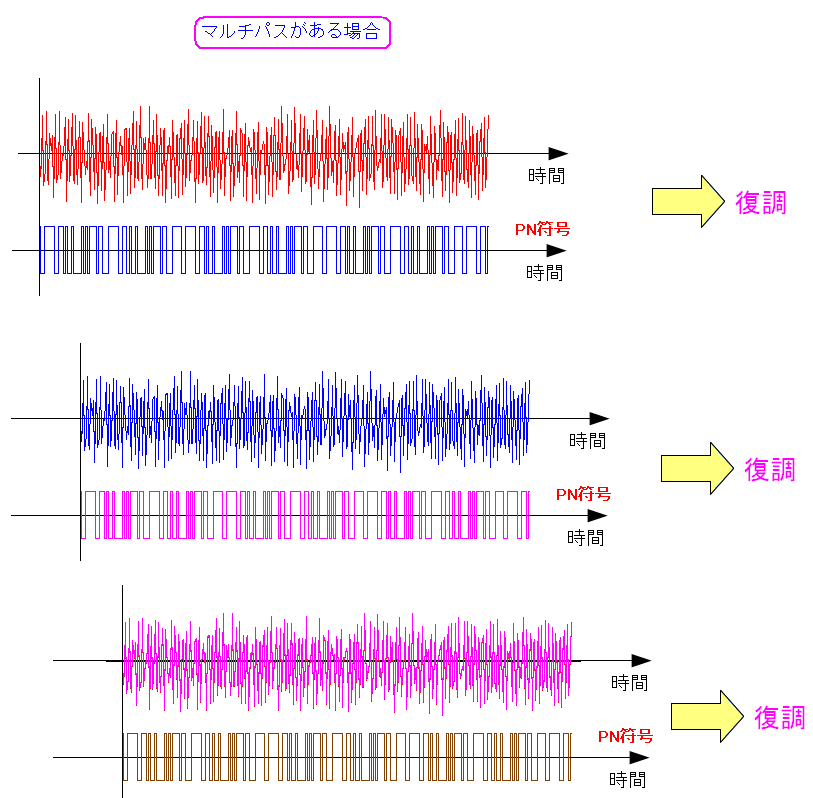 |
| PN符号を遅延波に合わせる事で、遅延波も復調できる。 |
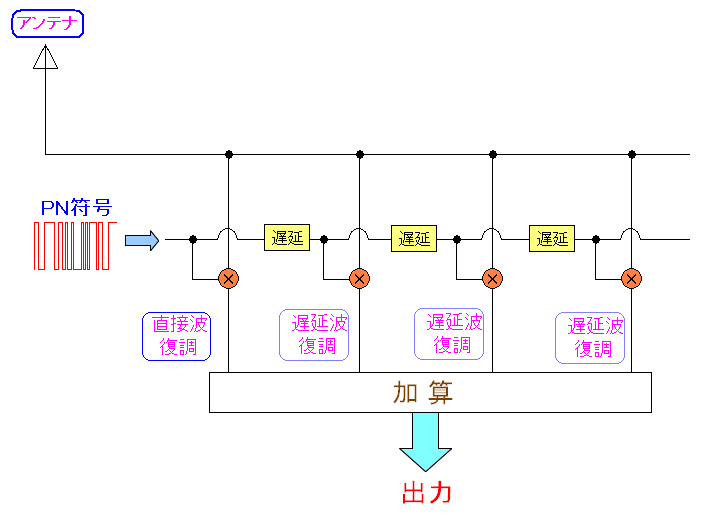
そこで以下のような仕掛けが受信側にあるという。
| RAKE受信機 |
|---|
 |
|
直接波、遅延波を、それぞれ復調して、それを足し合わせるという。 それにより、しっかりと信号を捕らえる事ができるというのだ。 マルチパスの現象を逆手にとった方法だ。 |
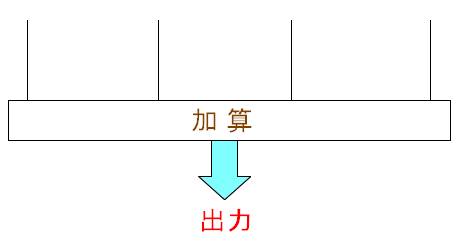
ところでRAKEというの言葉由来は、どこから来ているのか。 意外な物から来ているというのだ。
| 「RAKE」の由来 |
|---|
 |
|
熊手(RAKE)の形で信号を拾っているをしている事から RAKE受信機と言われているのだ。 |
CCK変調
CCKとは、直接拡散方式(DSSS)を高速化した技術だという。 早速、調べてみる事にした。 早わかり講座 広がる無線LAN(5)干渉を防ぐための通信方式(ITPro) 無線LANテック - 解説記事/コラム-CCK(しーしーけい) すると Complementary Code Keying の略だという。 直訳すると「相補符号」なのだが・・・ だから何やねん!! なのだ。 言葉の意味は横に置いておく事にして、どういう変調なのかを調べてみた。
| CCK変調とは |
|---|
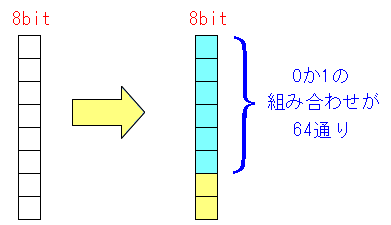 |
|
8bitのデータで、6bitに着目する。 「0」と「1」の信号の組み合わせなので 2の6乗で、64通りの組み合わせができる。 |
そこで以下のような事を考え出したという。
| CCK変調の仕組み |
|---|
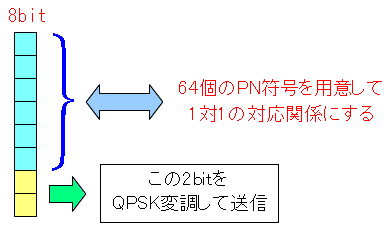 |
|
8ビットのうち、6ビットを対応するPN符号にしてしまう。 そして残り2ビットを、QPSK変調するのだ。 |
もし、2ビットをQPSK変調をすれば、1度に2ビットのデータを送れる。
| CCK変調で送信 |
|---|
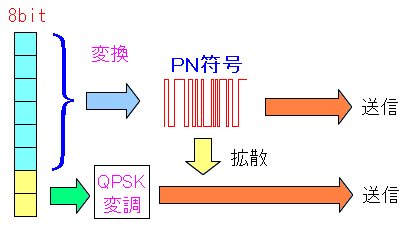 |
|
2ビットQPSK変調し、それをPN符号で拡散すれば 8ビットのデータを1度に送れるというのだ。 上手にデータ圧縮して送信した形になる。 |
そして復元方法は以下の通りになる。
| CCK変調で受信 |
|---|
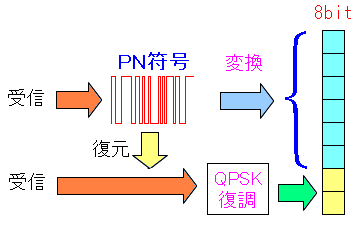 |
|
一緒に送ったPN符号を使って、復元を行なう。 PN符号は対応する6ビットに変換される。 拡散信号から復号されたデータは、QPSK変調の復元を行ない もとの2ビットデータに戻る。 |
ちなみに上で説明した8ビットを1度に送る方法を
CCK-64
という。
64通りのPN符号を使う事に由来しているようだ。
他にも、CCK4があり、4ビットのデータのうち、2ビットを
4通りのPN符号にして、残りの2ビットをQPSK変調で送る方式だ。
これだと1度に4ビットしか送信できなくなる。
CCK変調により、直接拡散方式よりもデータ送信量は大幅に増えた。
| IEEE802.11bでのデータ送信量の比較 | |||
|---|---|---|---|
| DSSS | CCK | ||
| DBPSK | DQPSK | CCK-4 | CCK-64 |
| 1Mbps | 2Mbps | 5.5Mbps | 11Mbps |
でも、PN符号を、そのまま送信するため・・・ 雑音に弱くなった という問題点が発生したのだ。OFDM変調の仕組み
2次変調で、直接拡散方式以外にも、OFDM変調がある。 再度、OFDMが何かを理解するための挑戦が始まった。 最初に理解した範囲は以下の通りだった。
| OFDMとは |
|---|
 |
|
まずは1次変換したデータを分割する。 そして分割した物を同時並行で送信する。 データを運ぶ経路が増えているので、データ送信速度が速くなるのだ。 |
どのように並行して送信しているのか。
| OFDMは周波数分割 |
|---|
 |
|
周波数を軸にとると、綺麗に整列させているのだ。 |
ここから先、進まねばならない。 まずは、OFDMとは Orthogonal Frequency Division Multiplex の略で日本語訳だと「直交周波数分割多重方式」なのだ。 だが・・・ 直交周波数分割多重方式って何やねん? なのだ。 日本語訳を見ても、何の事やら、わからん。 再度、いくつものサイトを見てみる事にした。 OFDM(北海道大学・情報科学研究科 インテリジェント情報通信研究室) ASCII.jp:ノイズに対抗する無線LANのスペクトラム拡散とは? (2/2)|無線LANのすべて そこで、色々なサイトを探してみると、いくつかの大学の講義資料が見つかった。 デジタル無線通信の基礎からOFDM入門まで(琉球大学:和田知久先生) 情報通信システム論I 無線LAN(物理層)(奈良先端科学技術大学院大学:岡田実先生) これらを 七転八転しながら 読んでいった。 まずは直接拡散の所でも出てきたが、1次変調した信号を スペクトラム分布の話が出てきた。 OFDMでも、その話は重要になるので、復習をしてみた。
| 1次変調した信号(搬送波)とスペクトラム分布 |
|---|
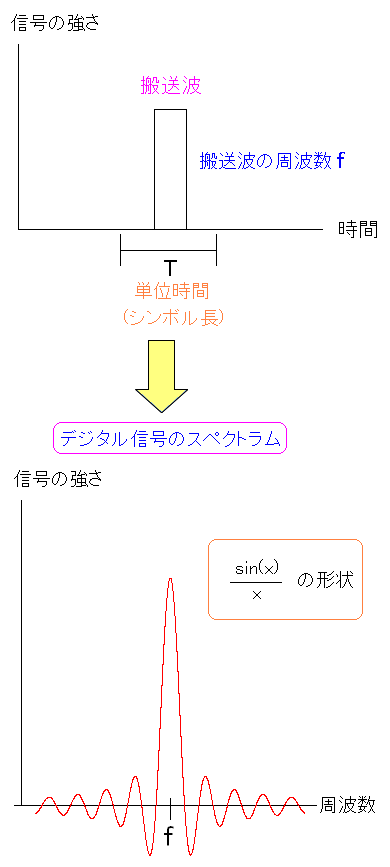 |
|
ASKといったパルス波や、位相変調(PSK、QPSK)やQAMでも 搬送波の周波数が「f」で、単位時間(シンボル長)を「T」の場合 スペクトラム分布は「f」を中心とした物だ。 |
そしてスペクトラム分布は以下の特徴を持つ。
| スペクトラム分布の特徴 |
|---|
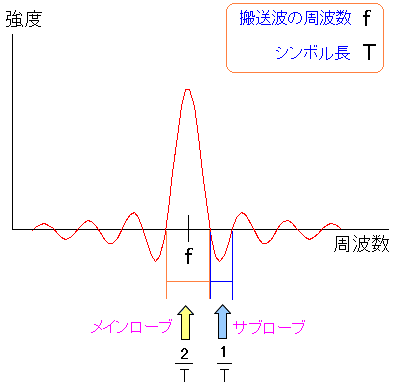 |
|
メインローブは(2/T)の幅になる。 そしてサブローブは(1/T)の幅になる。 |
OFDMは、複数の搬送波を使って信号を送っている。
| OFDMは複数の周波数の搬送波で送信 |
|---|
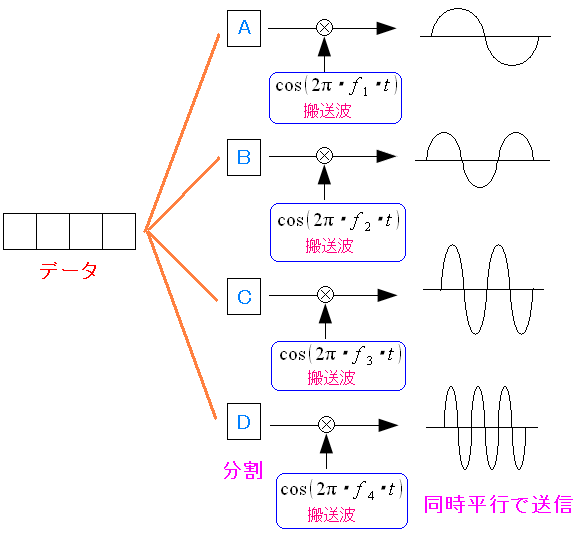 |
|
データを分割して、それぞれ周波数の違う搬送波を使って データ送信するのだ。 |
ところでOFDMの場合
搬送波がcosカーブで表現できるねん?
と思った。
OFDMの場合の1次変調は以下の物が使われる。
| OFDMで1次変調に使われる変調方式 |
|---|
| BPSK |
| QPSK |
| QAM16 |
| QAM64 |
| QAM256 |
資料を読むと
IQ座標を使った信号星座図
が出てきた。
QAM変調の部分で触れたが、ここでおさらい。
| 16QAMの信号星座図 |
|---|
 |
| 座標はI軸とQ軸をとる座標系だ。 |
信号星座図の見方は以下の通りになる。
| 信号星座図の見方 |
|---|
 |
|
I軸方向はcosΘ成分。 Q軸方向はsinΘ成分。 位相が搬送波の場合、 点Pの位置の振幅と位相のズレの搬送波の場合 cosΘ成分とsinΘ成分に分解する事ができる。 |
そして座標ごとに送信するビットの値が決まっている。
| 信号星座図とビットの値 |
|---|
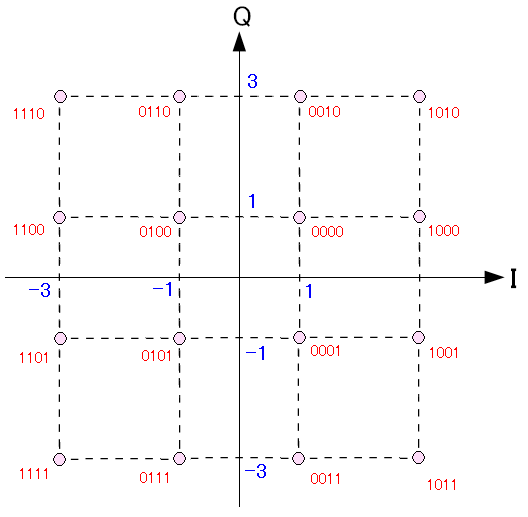 |
|
16QAMの場合、16通りのデータ(4ビット)が送信できる。 座標(3,1)の場合だと送信する信号のビット値は「1000」になる。 座標とビット値が1対1で決まるのだ。 (注意) 座標とビット値だが、ネットで調べていると 上図とは違う場合があるため、あくまでも参考にとどめてください。 |
ところで搬送波はcosカーブになる。
| 搬送波はcosカーブになる |
|---|
 |
|
cosカーブの搬送波。 三角関数の合成の公式を使って分解すると cosΘ成分とsinΘ成分に分解する事ができる。 |
ところで信号星座図を使う利点は、次のような事があるからだ。
| 信号星座図を使う利点 |
|---|
 |
|
送信したいビットに対応する座標が(a,b)の場合を考えてみる。 I軸方向(cosΘ成分)の大きさは「a」 Q軸方向(sinΘ成分)の大きさは「b」 搬送波の振幅や位相のズレを計算しなくても 座標の値を入力するだけで、合成波ができるのだ。 |
これで一次変調がQPSKでも、16QAMでも搬送波がcos関数になる事が わかったし、信号星座図の見方がわかったのだ。 OFDMでは、複数の搬送波を並行して送信している。 単に周波数がバラバラで並行に送信しているのではなく ある規則に基づいて送信しているのだ。
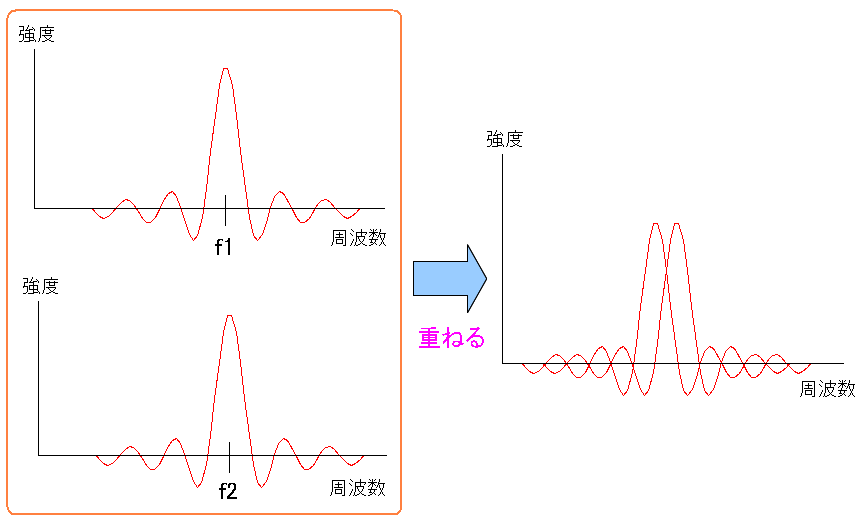
| OFDMでの複数の搬送波の送信方法 |
|---|
 |
|
2つのスペクトラム分布で、メインローブを ぴったしくっつけるように並べる。 |
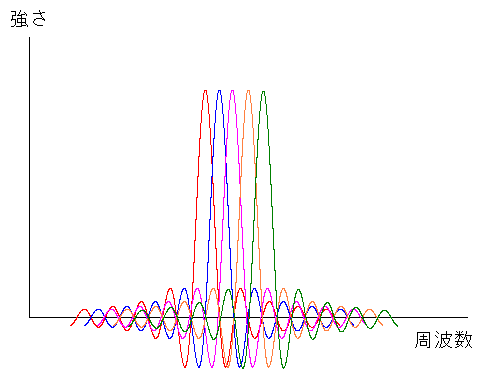
複数重ね合わせると、以下のようになる。
| OFDMでの複数の搬送波の送信方法 |
|---|
 |
|
メインローブ同士をぴったしくっつける。 そして個々のサブローブの幅が同じなので、上手に重ね合わせたようになる。 |
最初、OFDMの事を調べていた時、なんとなく わかった気になっていた のだった。 だが、この原稿を書いていると、実際には、わかっていない事が発覚。 どうやってメインローブをくっつけるのか? だった。 言葉で「メインローブを上手に並べる」と言われても 実際に、どういう規則性を用いて並べるのかは、わかっていなかった。 そこで調べ直す事にしたのだ。 OFDMで信号を送信するための搬送波の周波数と周期だが、 ちょっとした細工をしているのだ。
| スペクトラム分布の座標について |
|---|
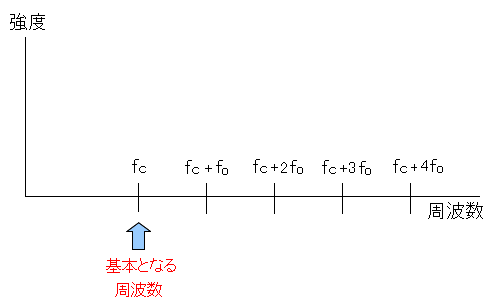 |
| 基本となる搬送波の周波数(fc)とし、各スペクトラムとの間隔をfoにする。 |
スペクトラム分布には以下の特徴がある。
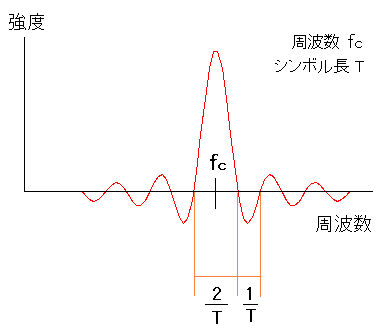
| スペクトラム分布の特徴 |
|---|
 |
|
周波数fcで、シンボル長Tの搬送波の場合 (1/T)間隔でスペクトラム分布の値が0になる特徴を持っている。 |
そこで以下のようにスペクトラム分布の座標を設定する。
| スペクトラム分布の座標を設定 |
|---|
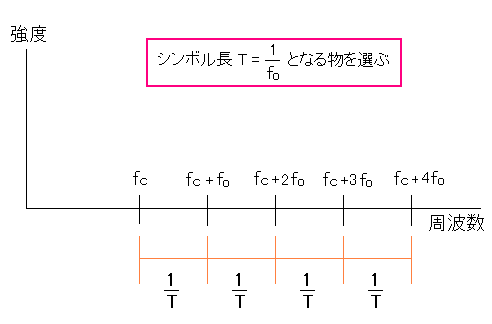 |
| 各スペクトラムの間隔fcが、シンボル長の逆数(1/T)になるようにする。 |
そこでfo間隔で、各周波数別のスペクトラム分布を見てみる
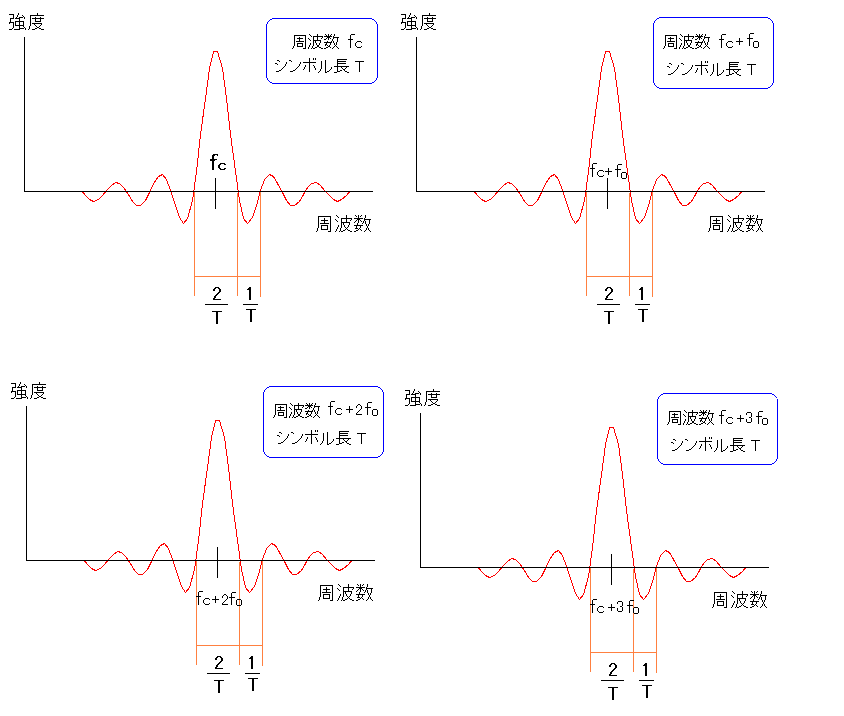
| 周波数別スペクトラム分布 |
|---|
 |
|
周波数の間隔をfoにした。 周波数が異なっていても、シンボル長を同じにすれば 各スペクトラムの形状は同じになる。 |
そこで上図のスペクトラム分布を重ねてみると以下のようになる。
| 各周波数でのスペクトラム分布を重ねてみる |
|---|
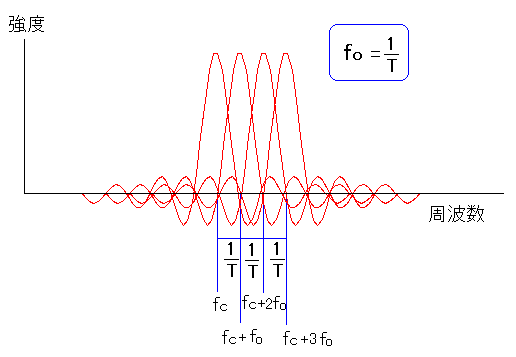 |
|
等間隔にスペクトラム分布を並べる事ができる。 これを実現させるには、シンボル長をどう設定するかが鍵になる。 |
ところでスペクトラムを重ねた場合、周波数帯域はどうみるのか、 以下のようにみるのだ。
| OFDMでの周波数帯域 |
|---|
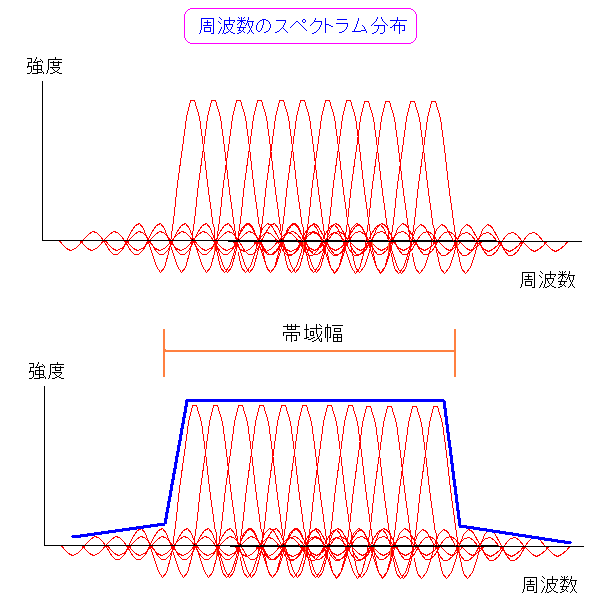 |
|
11a/11gでは20MHz。11nでは40MHz帯域を占有している。 11a/11gの場合、48本の搬送波と4本のパイロット信号。合計52本。 11nの場合は、104本の搬送波と4本のパイロット信号で、合計108本だ。 |
ところで
パイロット信号って何やねん?
なのだ。
この時点では、調べても、わからなかったのだが
少し踏み込んだ話を後述しています。
ここまでの話を整理してみる。
OFDMでの搬送波は以下のようになる。
| OFDMでの搬送波 |
|---|
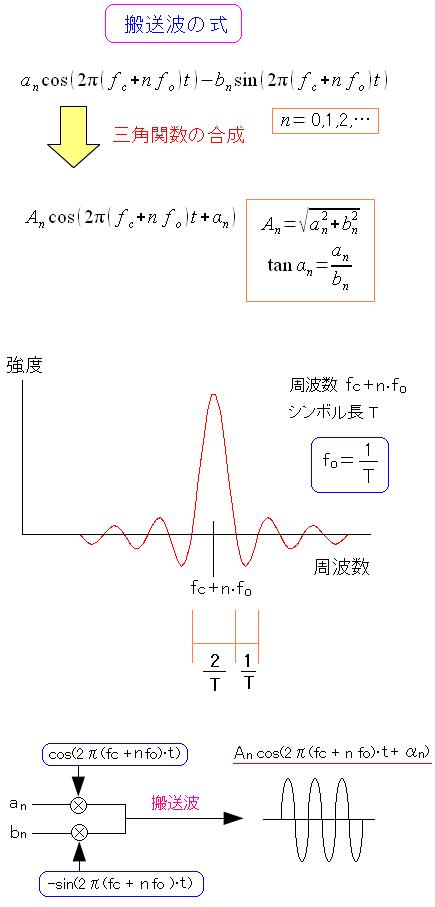 |
|
デジタル信号を信号星座図の座標(an,ab)に置き換えられる。 cos成分のanと、sin成分のbnの合成を行なうと、搬送波ができる。 三角関数の公式により、搬送波はcos関数で表現できる。 搬送波の基本周波数をfcとし、隣接する搬送波との周波数の差をfcとする。 この時、fcを、シンボル長Tの逆数(1/T)にしておく。 |
OFDMでは複数の搬送波を使って送信するため、以下のようになる。
| OFDMでは複数の搬送波を使ってデータ送信 |
|---|
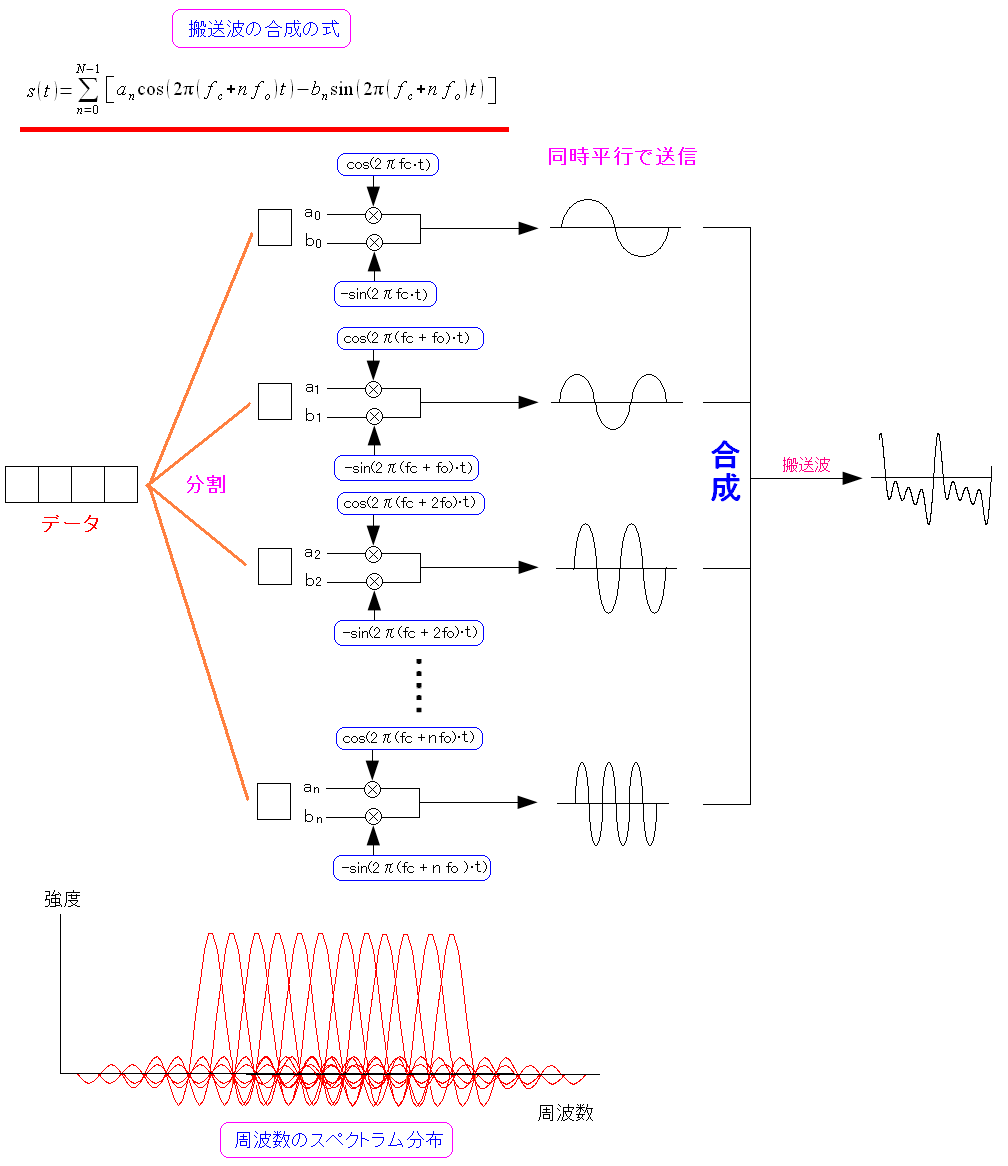 |
|
データを分割して、それぞれQPSKやQAM変調し、信号星座図の座標を使って 個々の搬送波を生成し、それを合成する形になる。 |
そして受信側を見てみる。
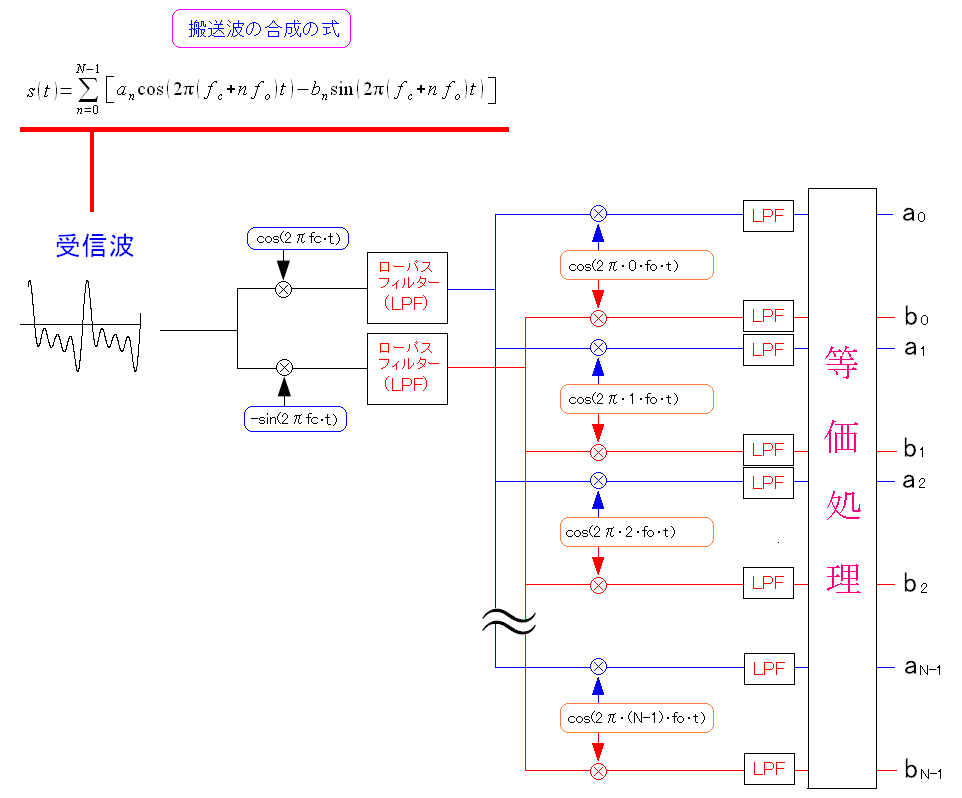
| OFDMの受信機の概略 |
|---|
 |
|
受信波から、フーリエ係数を取り出す。 フーリエ係数とは、一次変調(QPSKやQAM)の信号星座図の座標にあたる。 |
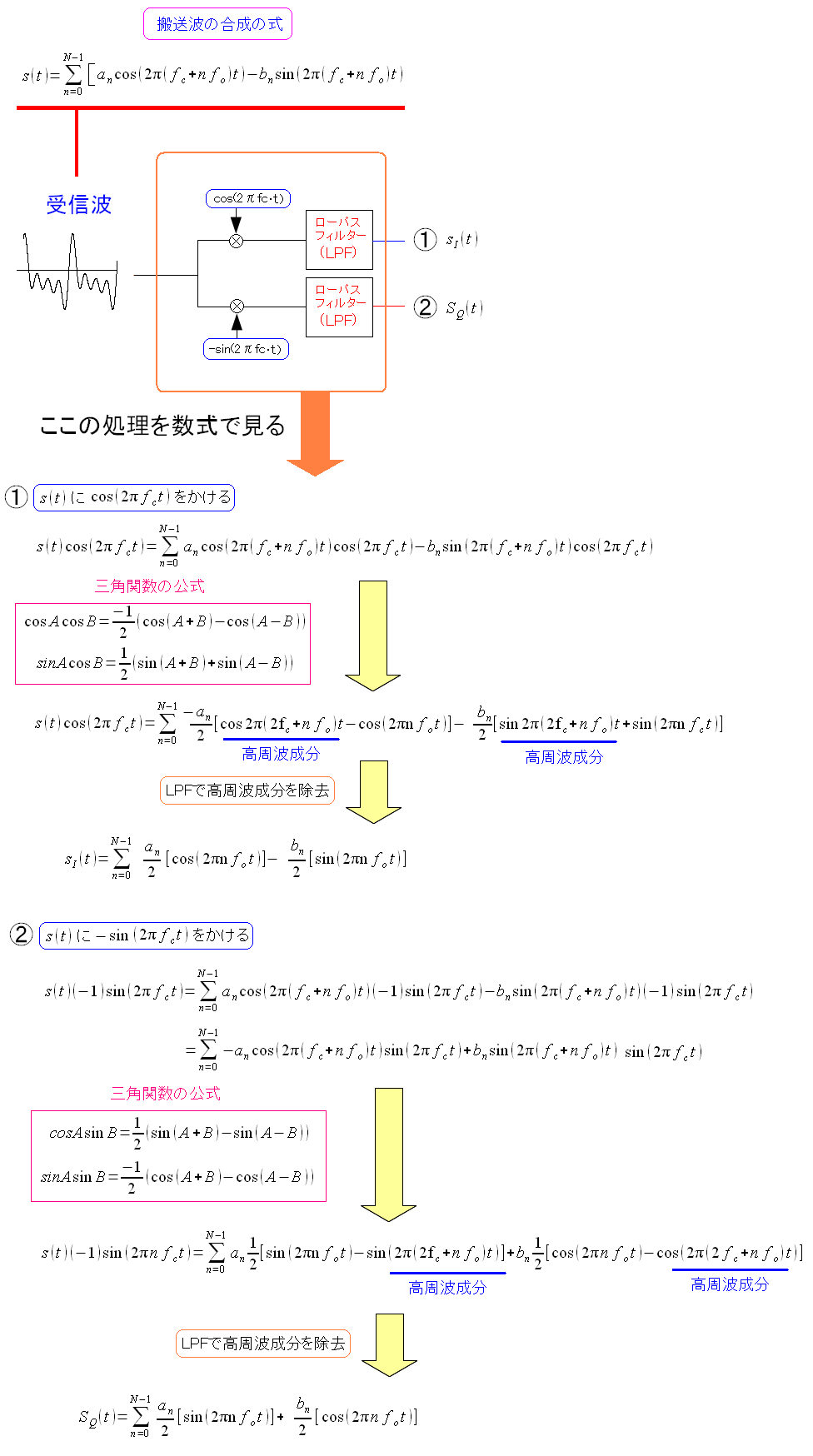
まずは最初の部分で、どのような処理が行なわれるのか見てみる
| 受信波の処理過程 |
|---|
 |
|
さすがに中の回路までは、わからないのだが 数学的な処理は上のような事を行なっている。 |
そして加工した信号を、さらに加工して、目的のフーリエ係数を取り出す。
| フーリエ係数を取り出す部分 |
|---|
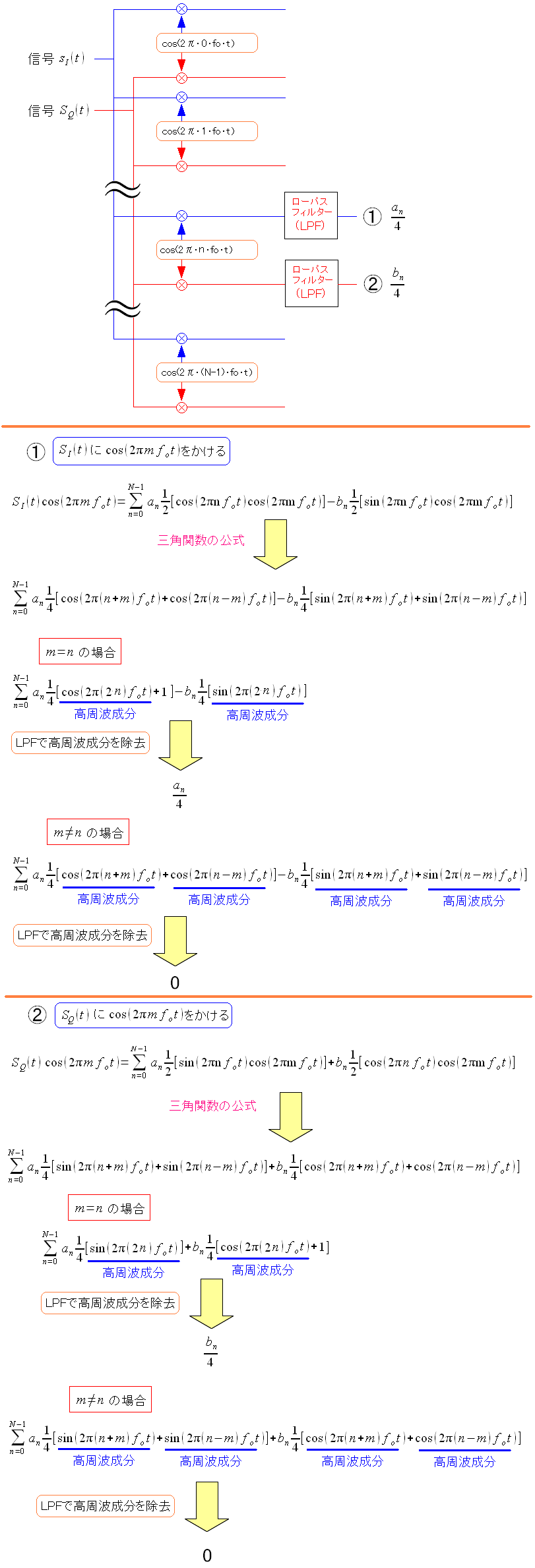 |
| ここも回路はわからないが、数学的処理だけを書いた。 |
なんとか説明ができたと思いきや・・・ アナログ回路での復調は困難 というのを知った。 OFDM変調からスペクトル(信号星座図の座標)を取り出すのは 離散フーリエ変換 を使うという。 ところで・・・ 離散フーリエ変換って何やねん? だった。
| 波形 |
|---|
 |
| 上図のようにy=f(x)の関数の波形があるとする。 |
もし、前もってy=f(x)の関数だとわかっていれば話は簡単だ。 だが、波形を受ける方は、どんな関数の波形なのか わからない事が普通だ。
| 波形と観測値 |
|---|
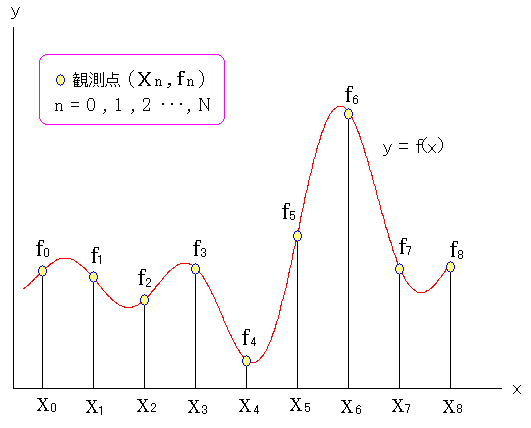 |
|
実際、波形を受け取る側は、波形の形を知らずに 有限個の観測点の値を受信しているのだ。 |
連続ではなく、離散的な観測値を扱うのだ。
| 離散フーリエ変換とは |
|---|
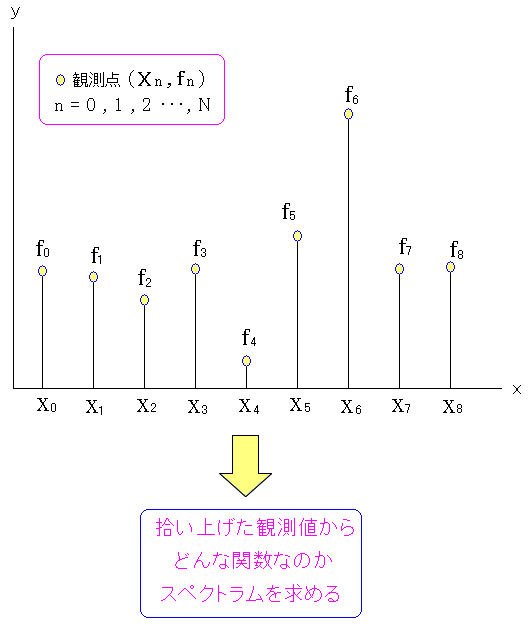 |
|
離散フーリエ変換とは、離散的な観測値から、観測している波形の スペクトルを求める計算方法なのだ。 |
いきなり離散フーリエ変換の話をしたくても
複素フーリエ級数を知らねばならぬ!
だった。
そこで複素数の範囲まで拡張したフーリエ級数の話を調べてみた。
| フーリエ級数と複素フーリエ級数の式 |
|---|
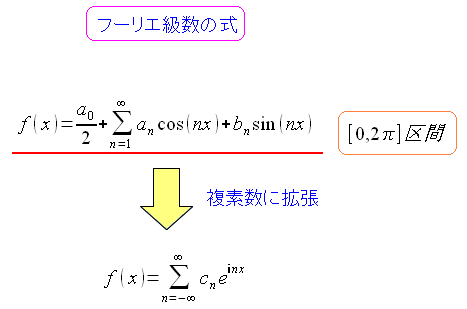 |
| 複素数の世界に拡張したフーリエ級数の式だ。 |
でも、複素フーリエ級数の式を導くのは、そんなに難しくない。 オイラーの定理と、ド・モアブルの公式を使えば導けるのだ。
| フーリエ級数から複素フーリエ級数の式を導く方法 |
|---|
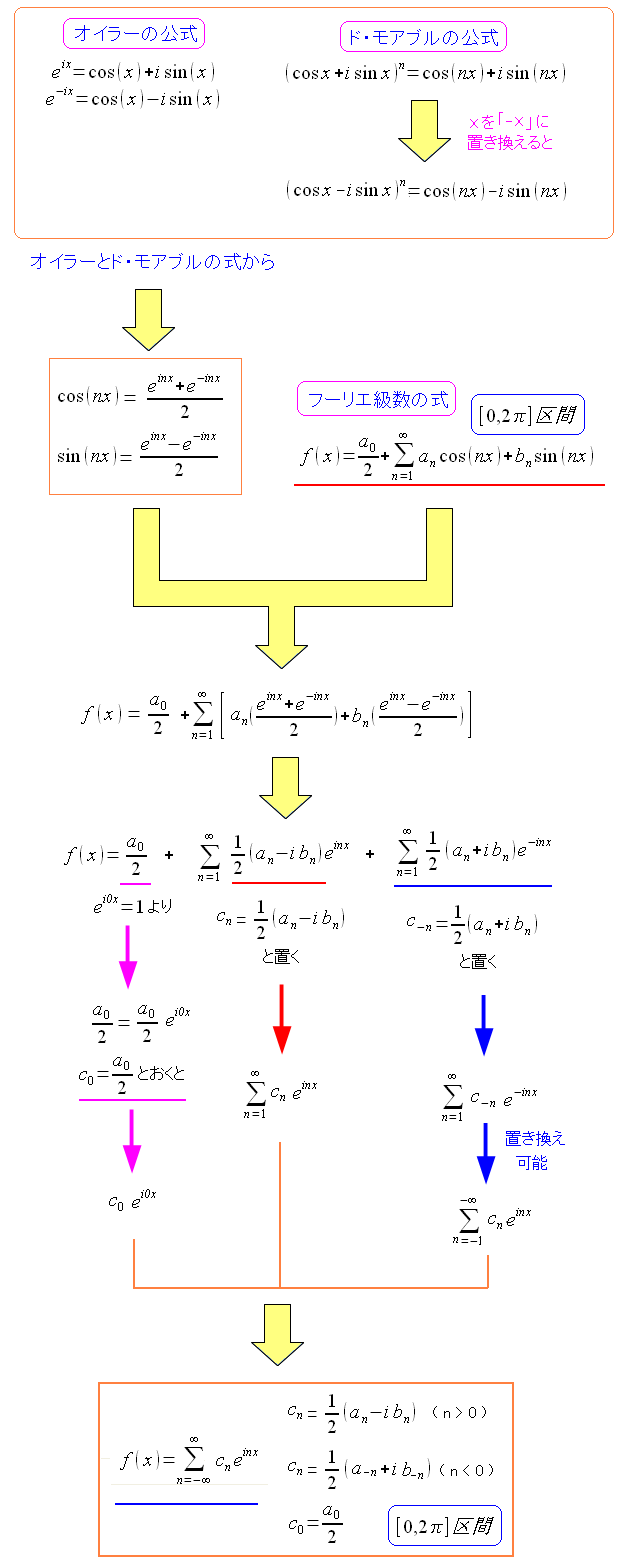 |
|
途中、ごまかしみたいな感じの部分があるのだが くれぐれも突っ込まないように!! |
複素数に拡張したフーリエ級数の式を導いた所で 離散フーリエ変換の話に入ります。
| 離散フーリエ変換と観測方法について |
|---|
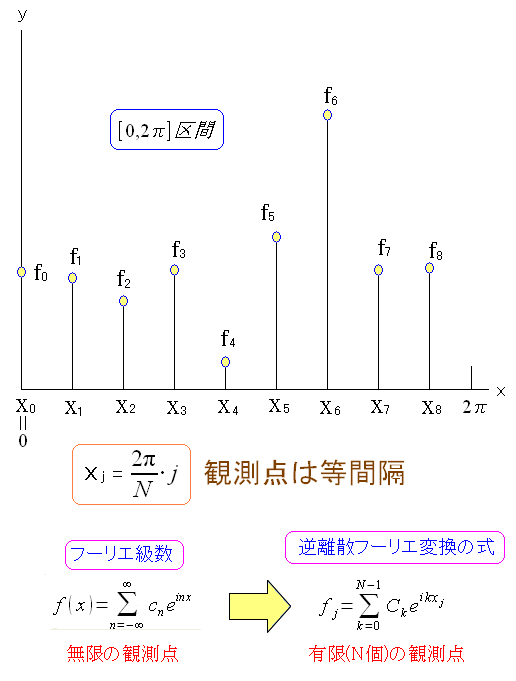 |
|
観測データに基づいて、やってきている波形の形と スペクトラムを求めるのが、離散フーリエ変換だ。 まずは連続の複素フーリエ級数と、逆離散フーリエ変換を見比べる。 観測値が離散的なので、逆離散フーリエの式になる。 |
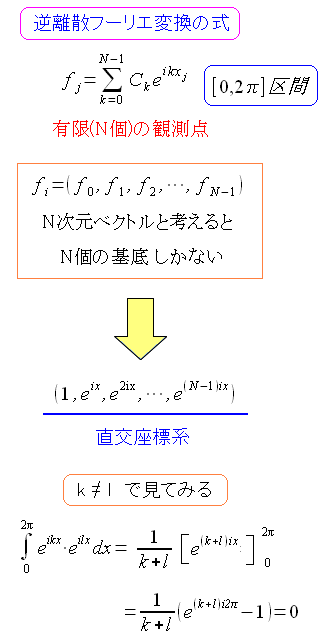
逆離散フーリエ変換の式を見てみる。 その前に直交性の部分を見てみた。
| 逆離散フーリエ変換の式 |
|---|
 |
|
フーリエ級数の場合、sin関数、cos関数で直交関数だった。 逆離散フーリエの場合、観測値が有限個のため、基底も有限個になる。 でも、直交性は守られている。 |
逆離散フーリエ変換では、既知の観測値を求める式になっている。
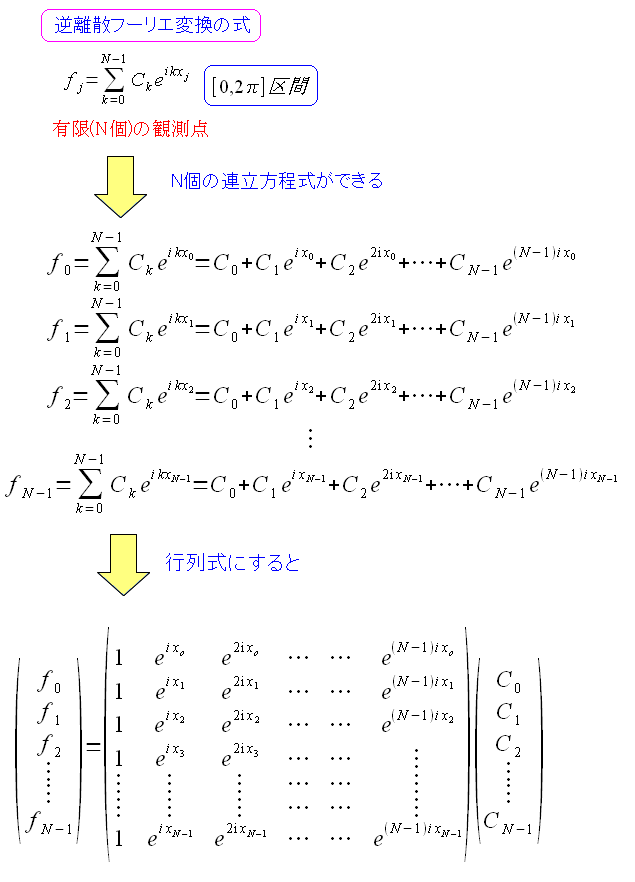
| 逆離散フーリエ変換の式を見てみる |
|---|
 |
|
逆離散フーリエ変換の式は、有限個の連立方程式になる。 これを行列で表現する事ができる。 |
でも、ここで計算が止まる。
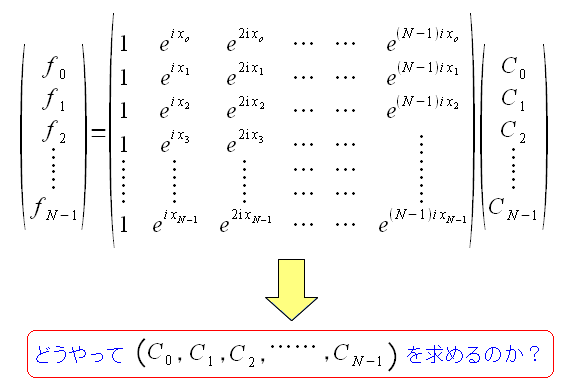
| 逆離散フーリエ変換の式を行列で表現したが |
|---|
 |
|
ここから先、スペクトラムのベクトルをどう算出するのか? 逆行列を求めて計算する方法もあるが、とんでもない計算量になる。 |
そこで以下のようにして、スペクトラムの値を算出するのだ。
| 逆離散フーリエ変換の式から離散フーリエ変換の式を求める |
|---|
 |
|
これでスペクトラムを算出する離散フーリエ変換の式が導けた。 観測値を代入するだけで、スペクトラムが算出できるのだ。 |
ところで上図の式で、場合わけしている箇所がある。
いきなり「この式はこうだ」になっている。
もちろん、私も・・・
これだとわからへん!
なので、導く事にした。
| 導きかた |
|---|
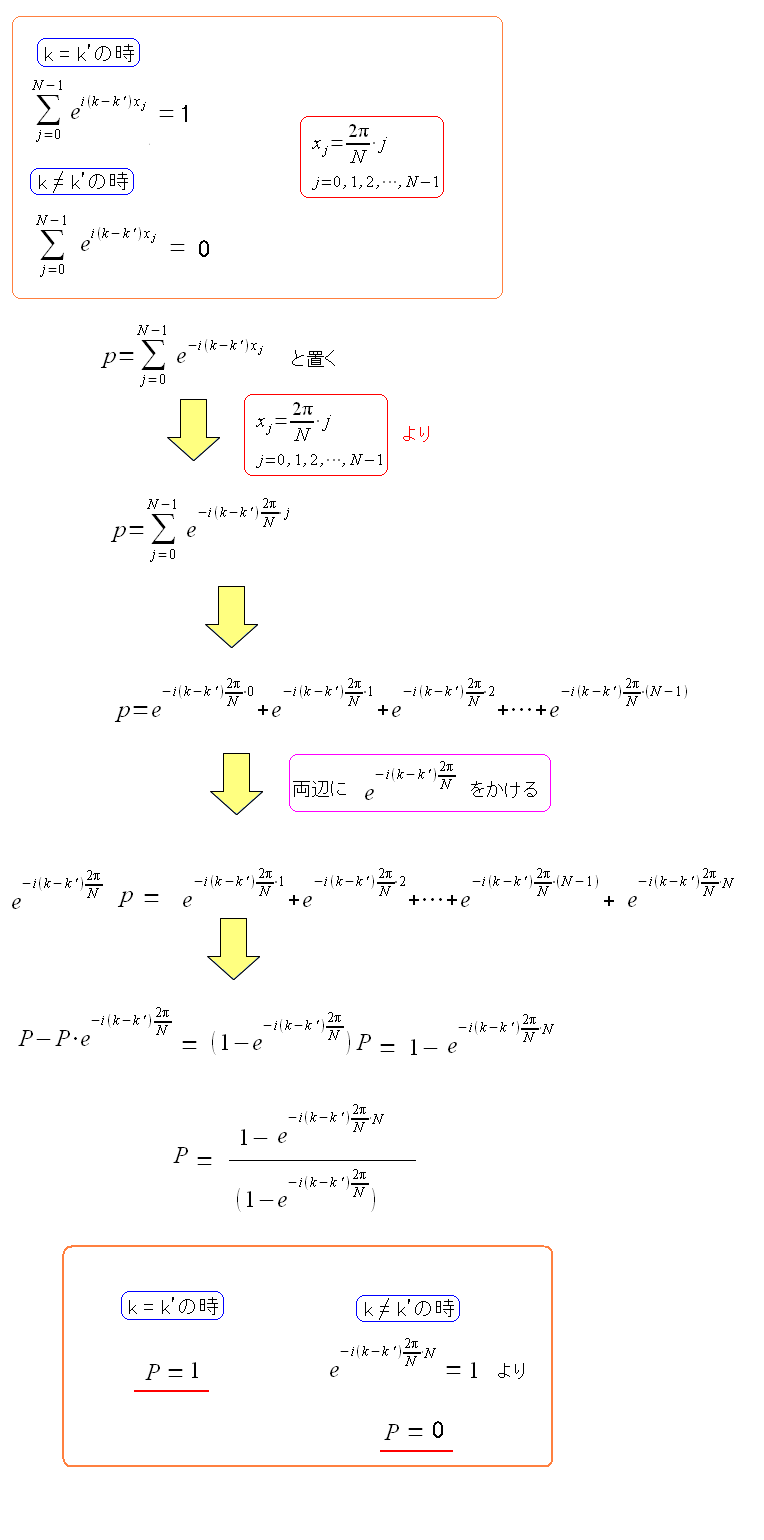 |
| まるで高校の数学で習った等比数列の和の導き方と同じだ。 |
そして離散フーリエ変換の式を連立方程式にして それを行列表現すると以下のようになる。
| 離散フーリエ変換の式を行列表現する |
|---|
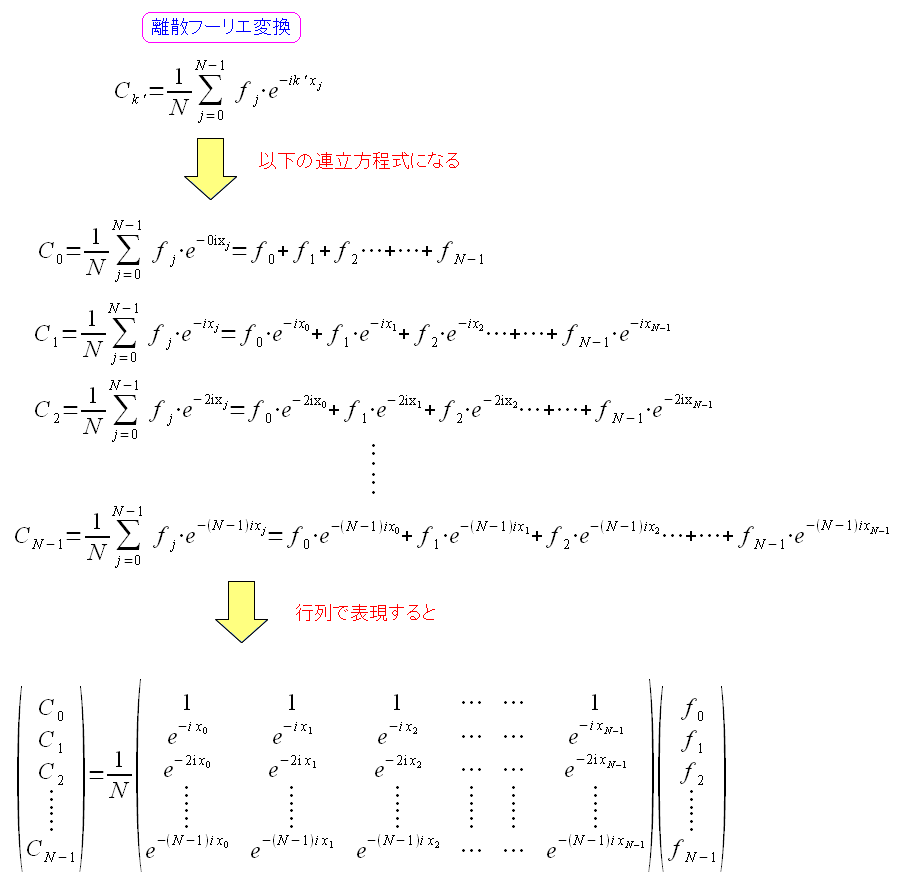 |
| 離散フーリエ変換の式を行列式で表すと見やすくなる。 |
というわけで、OFDMでの復調の仕組みは以下のようになる。
| OFDMでの復調の仕組み |
|---|
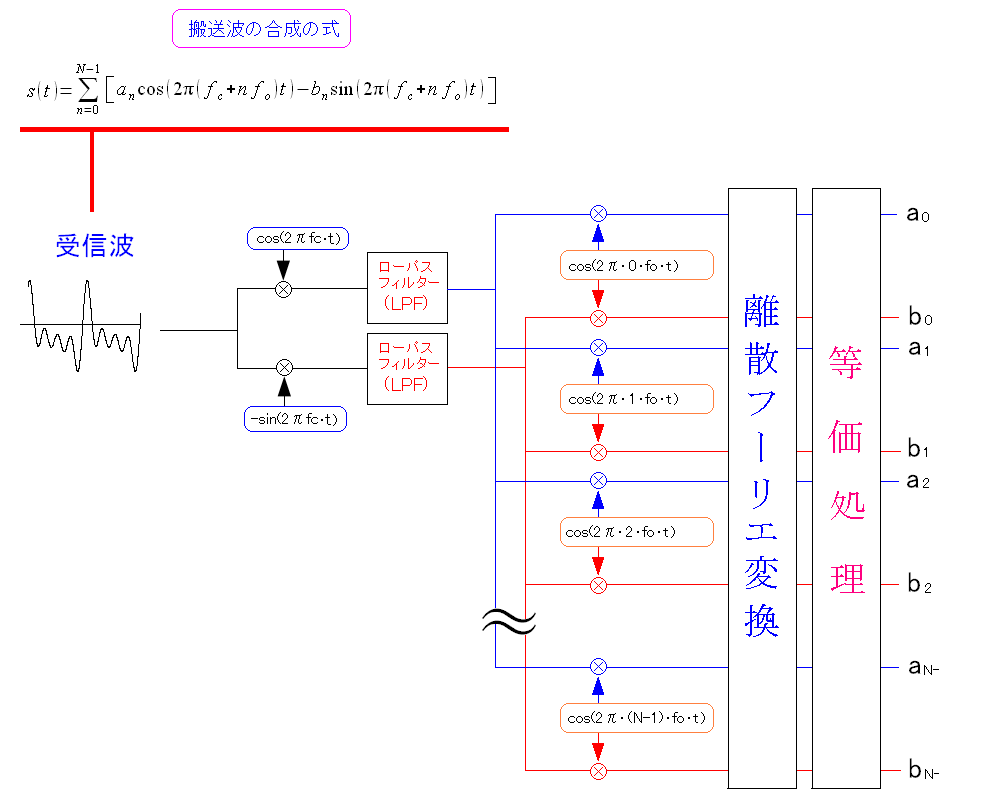 |
|
離散フーリエ変換の装置を入れて、スペクトルを取り出す仕組みだ。 デジタル処理で行なえるため、同期がとれるという。 アナログでは同期が取れるのが困難で、デジタルでは同期をとれるのかは 私には理解できなかったので省略します。 |
離散フーリエ変換処理を行なう装置は、以下ように受信波から スペクトルを取り出している。
| 離散フーリエ変換の処理装置 |
|---|
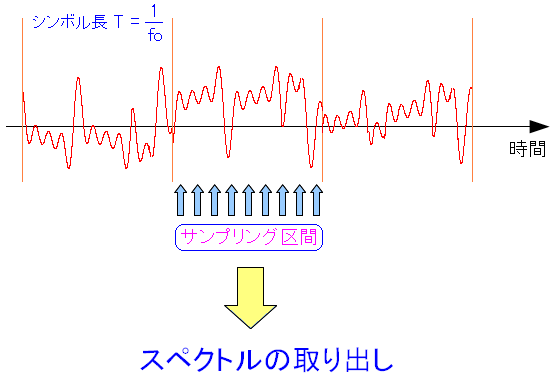 |
|
受信波を等間隔で観測し、その観測値を元にして 離散フーリエ変換装置で、QPSKやQAMの信号星座図の座標になる スペクトルを取り出すのだ。 |
離散フーリエ変換も観測地点の数が多くなれば計算量が増える。 そこで、高速に計算できる方法として考え出されたのが 高速フーリエ変換 (FFT) なのだ。 でも、そこから先、調べる気が起こらない。 なぜなら・・・ そこまで調べる馬力はないのらー!! というわけで、あっさりと諦めたのだ。 高速フーリエ変換(FFT)は別に機会に取り上げたいと思います。
| 数値計算の手法について |
|---|
|
今のようにコンピューターの性能が良ければ 力業で計算する事もできるが、昔は、そんなわけにいかなかった。 そのため、できるだけ計算量を少なくする方法が考え出された。 その1つが高速フーリエ変換だ。 もちろん、現在でも力業ではなく、高速で処理するために 数値計算の方法が考え出されているのだ。 |
ところで受信機の概略にあった 等化処理は何をする装置やねん! と言われそうなで、等化処理の話をします。 等化処理とは 遅延波の修正する処理 なのだ。 無線LANや携帯電話の電波の場合、パルチパス問題はつきまとう。
| マルチパスによる遅延波 |
|---|
 |
|
受信電波には、直接波と反射波がある。 反射波の場合、より長い距離を通っているため 遅れてやってくる。これを遅延波という。 |
マルチパスがあると以下の問題があるという。
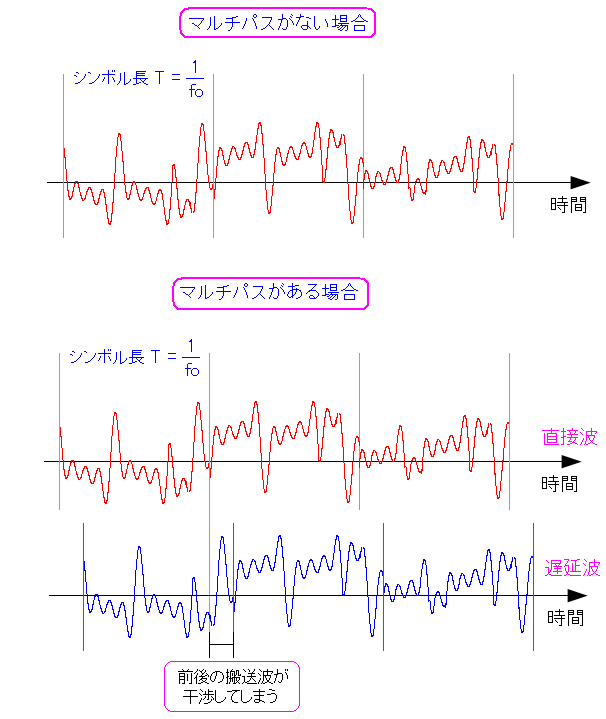
| OFDM方式でのマルチパス問題 |
|---|
 |
|
マルチパスがない場合、直接波だけを受信すれば良いので問題はないが マルチパスがある場合、直接波と反射波が干渉しあう問題が発生する。 |
直接拡散方式(DSSS)では、RAKE受信でマルチパス問題を解決していた。 OFDMでは、ガードインターバル(GI)を使っているのだ。
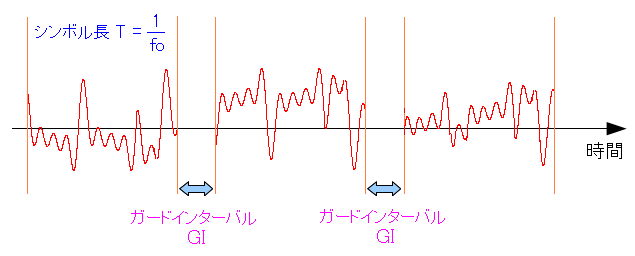
| ガードインターバル(GI)とは何か |
|---|
 |
|
1シンボルごとに、すき間を開ける。 そのすき間をガードインターバルという。 英語だと「Guard interval」なので、直訳すると「保護間隔」になる。 |
ガードインターバルを設ける事で、前後の信号との干渉を 防ぐ事ができる。
| ガードインターバルを設ける事で干渉を防ぐ |
|---|
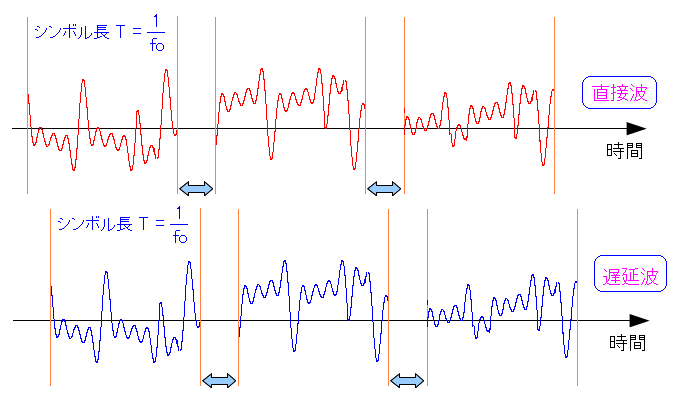 |
| ガードインターバル区間を、どれくらいの時間にするかが問題になる。 |
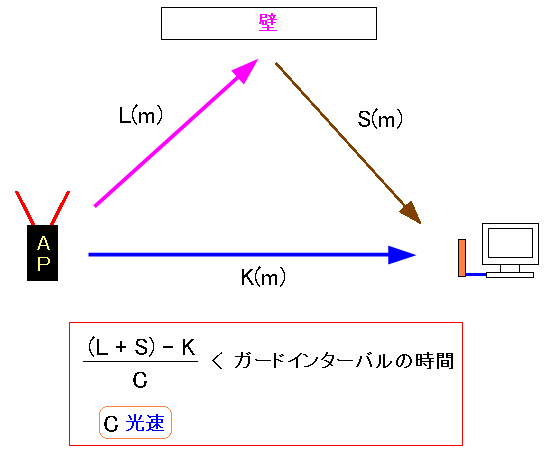
ところでガードインターバルの長さをどう決めているのか。 遅延波が、どれくらい遅れてやってくるのかに依存する。
| 直接波と遅延波との到達時間の差 |
|---|
 |
|
単純に考えると、直接波と遅延波との到達時間の差が ガードインターバルの範囲に収まる必要がある。 電波は光の速度と同じなので、単純計算すると上の関係式が成り立つ。 |
ところで実際に、ガードインターバルの時間はどれくらいなのか 調べてみると、見つかった。 高速無線LAN情報局 IEEE802.11nの高速化技術 (3)
| 行程差の計算 |
|---|
 |
|
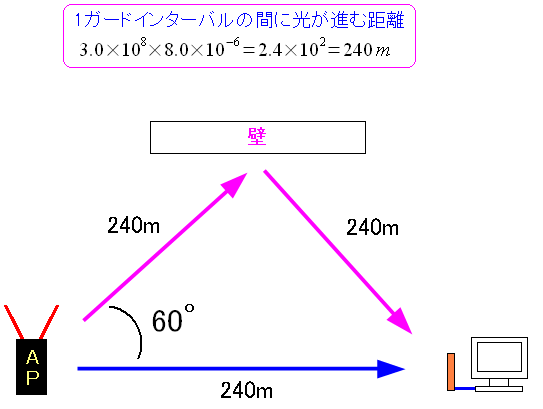
ガードインターバルは0.8マイクロ秒だ。(11a,11gの場合) そこで、直接波と遅延波との間で、どれくらいの行程差が 許されるのか、単純計算したら、240mと出た。 |
240mの行程差まで許される。 どんな環境なのか図にすると、わかりやすい。
| 240mの行程差 |
|---|
 |
|
横240m、縦140mの部屋で、それぞれの端に無線アクセスポイントと 無線アダプターを置いた状態になる。 こんな事務所、ありえないぞと思ったりする。 |
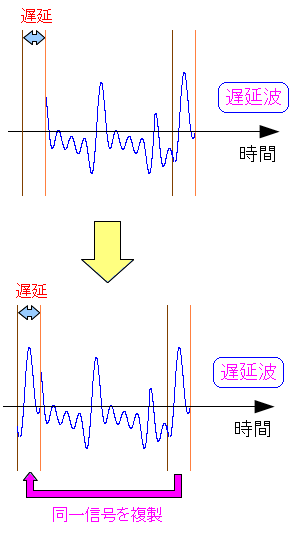
相当、余裕をもって ガードインターバルが設けられている のだ。 あまりにも余裕がありすぎるため、IEEE802.3の11nからは 0.4マイクロ秒 になったのだ。 高速無線LAN情報局 IEEE802.11nの高速化技術 (4) 話を元に戻して、遅延部分を補正する仕組みになっている。
| 遅延波の補正方法 |
|---|
 |
|
直接波と合わせるため、上図のように、はみ出して遅延した部分を コピーして前にもっている。 |
だが、これだけだと信号星座図が歪んだ形になっている。
| マルチパスの影響で信号星座図が歪んでいる |
|---|
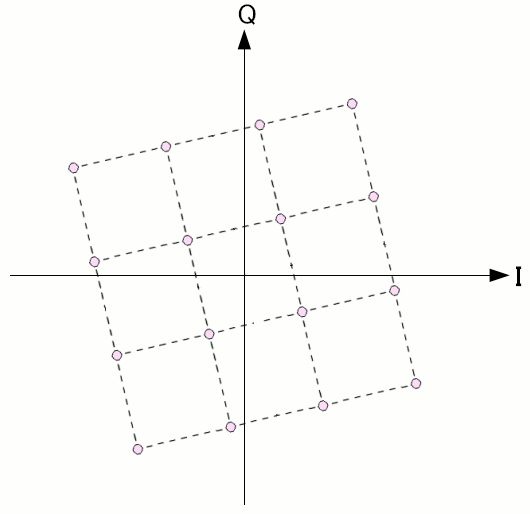 |
|
直接波と遅延波が重なる事で、離散フーリエ変換の処理装置で取り出した スペクトル(信号星座図の座標)では、上図のように歪んだ形になっている。 この歪みを直すのが、等化回路なのだ。 |
この歪んだ形を補正する必要がある。
| 等化とは |
|---|
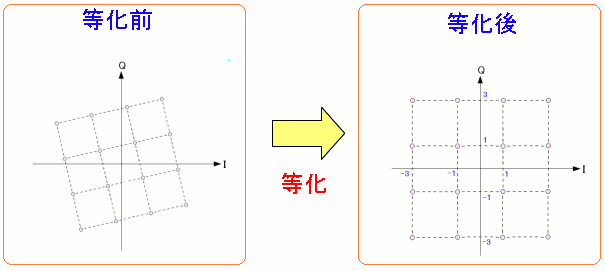 |
| 歪んだ信号星座図を上図のように補正する処理なのだ。 |
ところで、等化処理とはどんな処理が行なわれるのか。 調べてみると以下のPDF資料に載っていた。 OFDMと周波数領域等化 - 岡本英二(名古屋工業大学)
| 等化の式 |
|---|
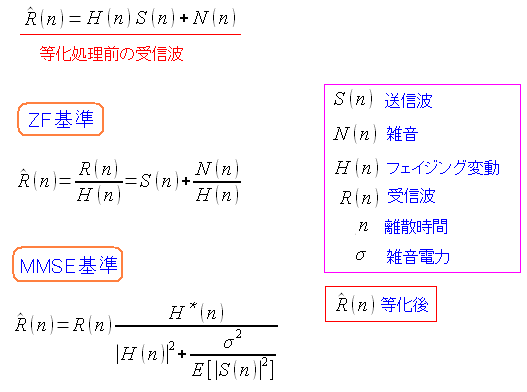 |
|
これがマルチパスで起こった干渉による歪みを直すための式だという。 ZF基準と、MMSE基準の二種類あるという。 |
この式を、どうやって導くのかを調べてみたのだが 等化処理に関する資料が見つからへん だった。 そして、仮に資料が見つかっても 理解できへん だったと予想できる。 そのため簡単に式だけ紹介して逃げる事を考えた。 そこで以下のPDF資料の内容を紹介して、適当に切り上げようと思った。 OFDMの基礎と応用技術(解説論文)
| 送信波と受信波の式 |
|---|
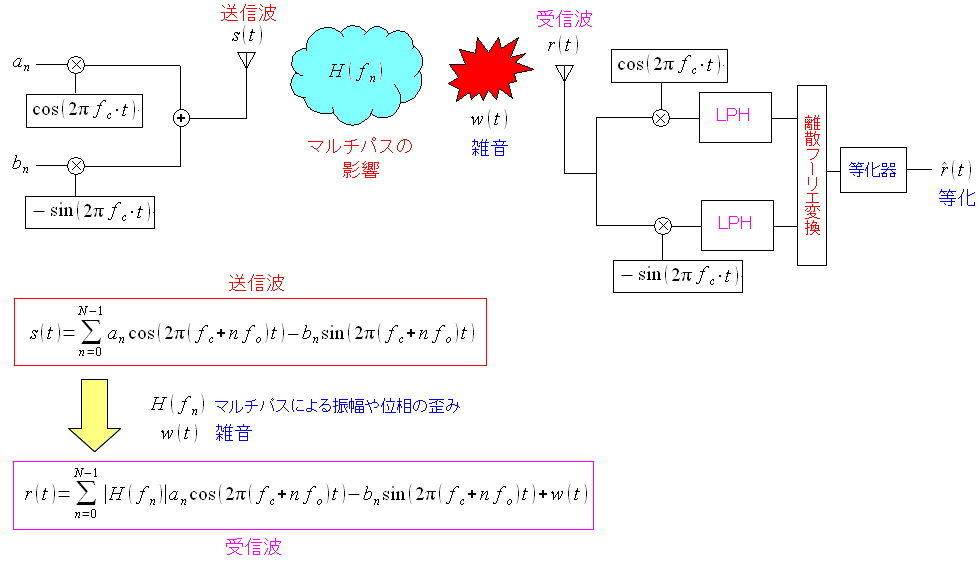 |
|
1次変調(QPSK,QAM16,QAM64)の後、OFDM変調をすると 上記の送信波の式になる。 送信波は途中の経路で、マルチパスや雑音の影響を受けるため 受信した際は、上記の受信波の式になる。 |
そして受信波の加工が行なわれる。 搬送帯域の周波数fcから、基底帯域の周波数foの信号に変換するための加工だ。
| 受信波の加工 |
|---|
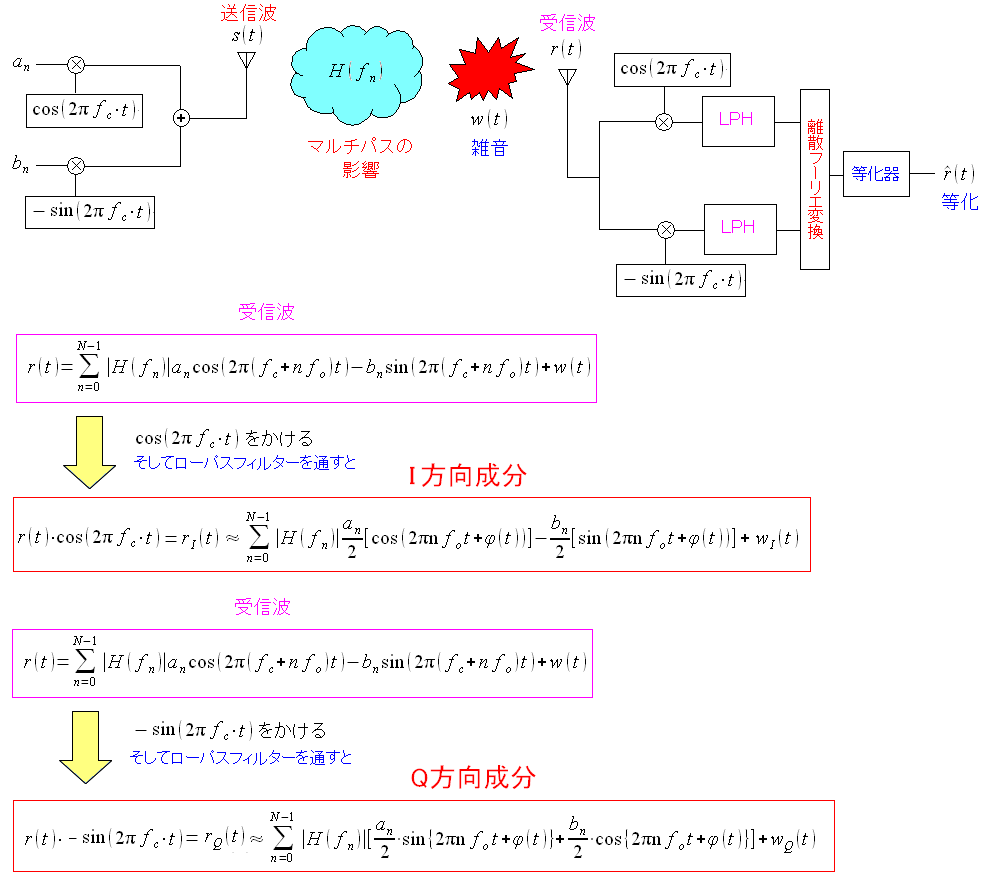 |
|
I方向(cos方向)のQ方向(sin方向)にわける事ができる。 ローパスフィルター(LPH)は、積分回路とも言われる。 受信波にcos成分をかけて、LPHを通す事で、sin成分を除去する。 それによってcos方向(I方向)を抽出する。 受信波にsin成分をかけて、LPHを通す事で、cos成分を除去する。 それによってsin方向(Q方向)を抽出する。 |
受信波をI方向とQ方向の成分に分解した。 次に、計算をしやすくするため、複素数の形にする。 虚数iは、90度の回転を意味する。 複素数については「システム奮闘記:その98」をご覧ください。 電気回路入門
| 複素数を使って計算の続きを行なう |
|---|
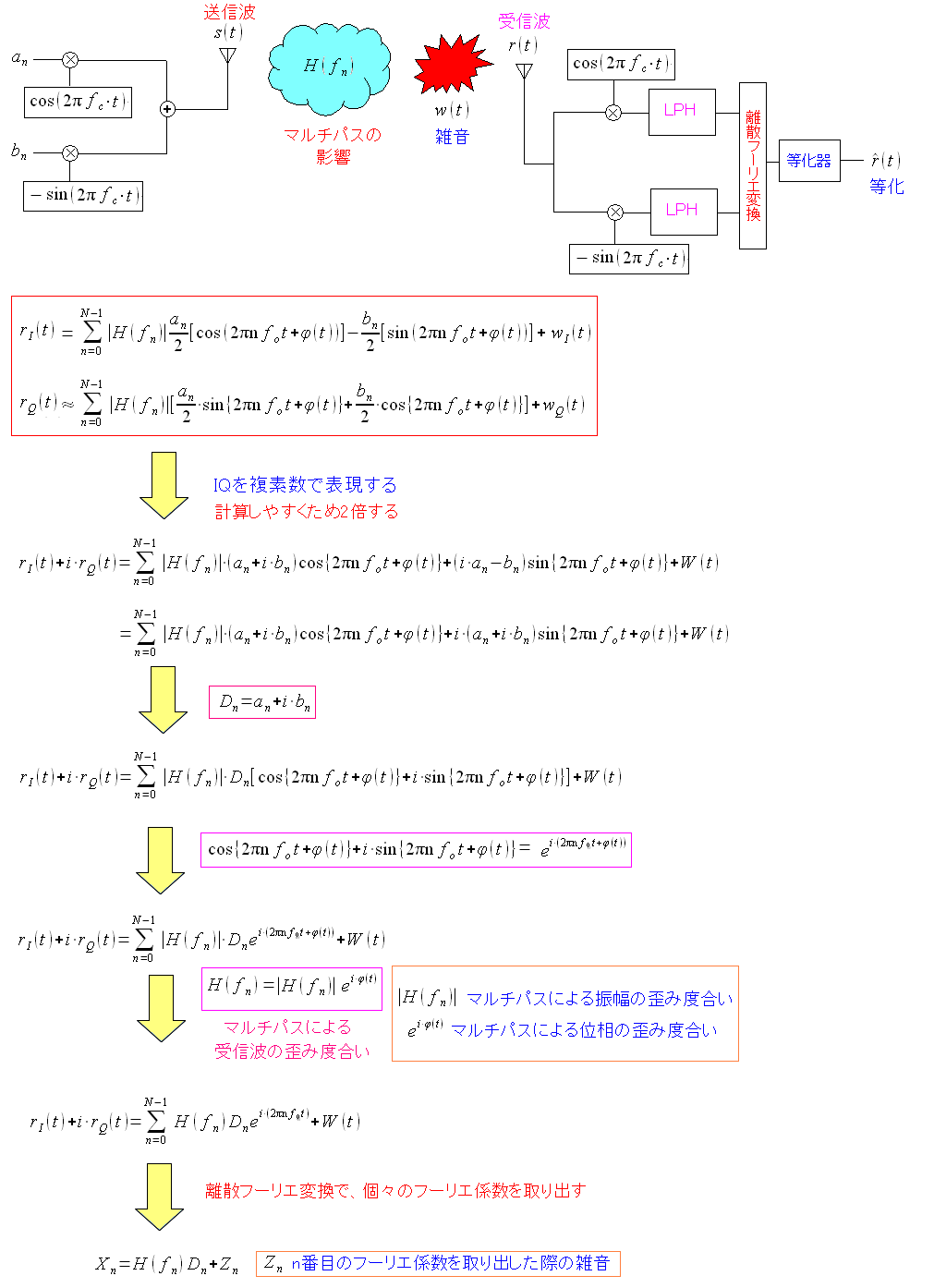 |
| 検出したスペクトル(Xn)の式が導けた。 |
ところで復調したいのは、元のスペクトラムの推定値。 そのためには、推定値を求めるための方法を知りたいのだ。
| 知りたい事 |
|---|
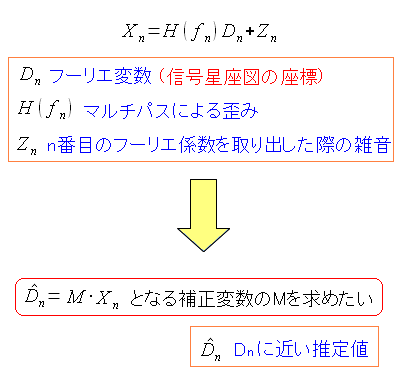 |
推定値を求める方法の1つにZF基準がある。
| ZF基準 |
|---|
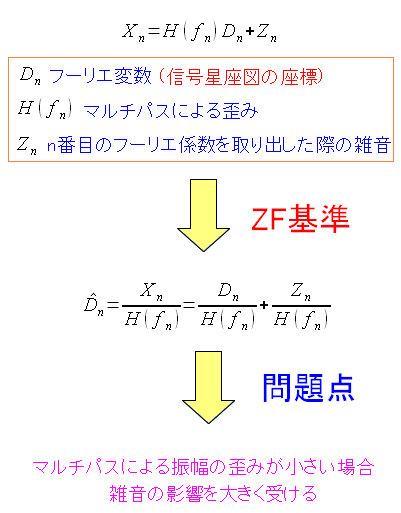 |
|
だが、この方法だとマルチパスによる歪みの影響H(fn)が 小さければ小さいほど、雑音の影響が大きくなる問題が起こる。 |
では、MMSEの場合なのだが・・・
MMSE基準の式は導いてへん
なのだ。
資料を見て、受信信号の処理を数式で追っかけただけで
肝心の式を導いていないのだ。
振り出しに戻った感じだ。
| MMSE基準の式 |
|---|
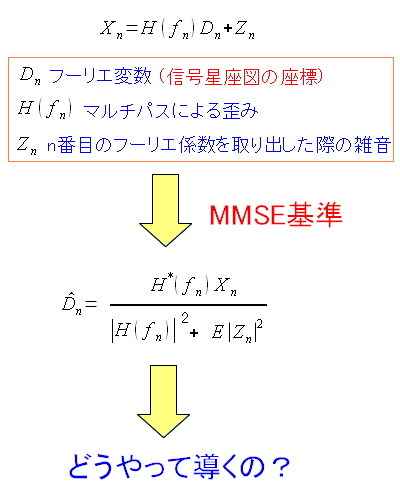 |
こんなの事務員にわかるか!! といわけで総務部員の立場を利用して、さっさと逃げようと思った。 でも、往生際の悪い私は、逃げようと思いつつも、ネット検索していると 気になる語句を見つけた。 ウィナーフィルター (Wiener Filter) だった。 そこでウィナーフィルターで調べてみると、以下の資料が見つかった。 信号処理の実例(京都大学)
| MMSE基準とは |
|---|
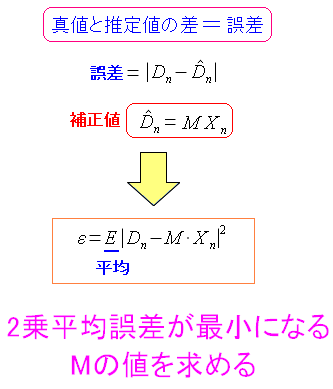 |
|
MMSEとは最小2乗平均誤差という意味だ。 そのため、上のような2乗平均の誤差の最小値を求めるというのだ。 |
そこで資料を参考にして、補正のMMSE基準の式を導いてみる事にした。
| MMSE基準の式を導いてみる |
|---|
 |
|
「DnとZnは、それぞれが独立」というのは、資料の受け売りなのだ。 なぜ、確かに依存性はなさそうなのだが、数式で証明したわけでない。 そして、積の和が0になるのは、内積の和がゼロの意味に思えるが それも数式で証明したわけでないのだ。 でも、ここで立ち止まっては前に進まないので、先に進めた。 これを忍法「先送りの術」という。 |
MMSE基準での等化の式が求まった。
ところで・・・
最小2乗平均誤差とは何やねん?
なのだ。
折角、式を導きだせても、その根拠になっている最小2乗平均誤差の意味を
知らなければ、ただの資料の受け売りに終わってしまう。
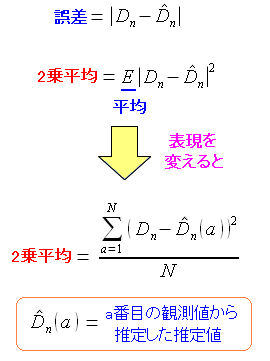
| 最小2乗平均誤差とは |
|---|
 |
|
どうして最小2乗平均誤差を求めるのか気になった。 調べてみると、2乗平均は分散である事がわかった。 実際、上記のようにN個の推定値があったとする。 そこで式を展開させると、分散である事がわかる。 真値に近い推定値を求めたい場合、分散が最小になるようにすれば良い。 真値に近い推定値を算出するのが、最小2乗平均誤差の目的だ。 |
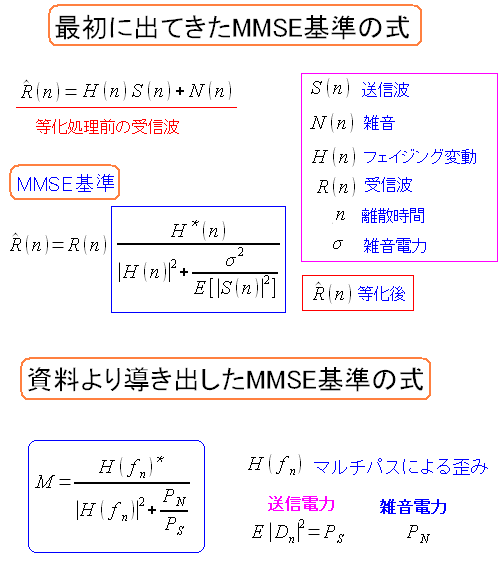
ところで、最初に資料で見た、等化の式と、導いた等化の式とを 照らし合わせると、表現こそ違うが、同じ意味の式になっている。
| 等化の式 |
|---|
 |
|
ところで資料を見ると、実際の雑音電力がどれくらいなのかは 正確には測定できないため、近似値を使っていると書いていた。 どういう近似値なのかについては、わかりませんで逃げます。 |
パイロット信号
ところで・・・ どうやってH(fn)を求めるねん? 歪みを推測するのに使われるのが、パイロットシンボルと呼ばれる物だ。 デジタル放送の場合、以下のような事をしている。
| デジタル放送などの場合 |
|---|
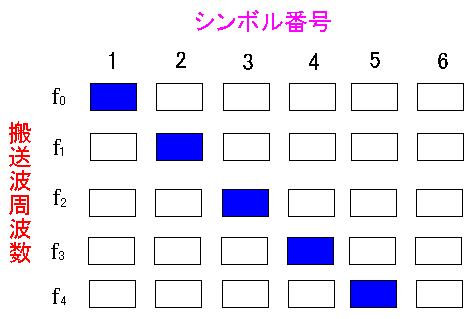 |
| 各搬送波にパイロットシンボルというものを挿入する。 |
無線LANの場合は、以下のようになる。
| 無線LANの場合 |
|---|
 |
| パイロット信号専用の周波数を設ける。 |
スペクトラム分布で見ると、こんな感じだ。
| OFDM 無線LANのパイロット信号 |
|---|
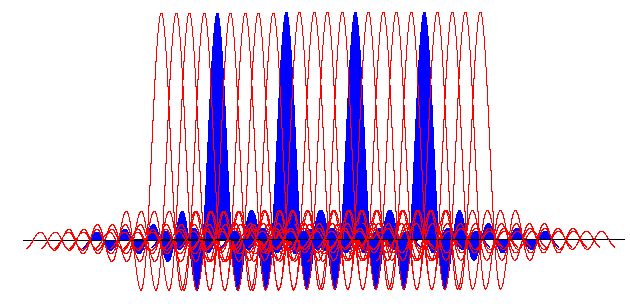 |
| どの規格でも、パイロット信号は4本ある。 |
無線LANの規格と搬送波・パイロット信号の数を表にしてみる。
| 無線LANの規格と搬送波・パイロット信号の数 | ||
|---|---|---|
| 規格 | 搬送波の数 | パイロット信号の数 |
| 11a | 48 | 4 |
| 11g | 48 | 4 |
| 11n(20MHz) | 52 | 4 |
| 11n(40MHz) | 104 | 4 |
パイロット信号が発信するデータの中身は、受信側もわかっている。 そのため、受信側は、送信されるデータと、受信したデータとの 比較が行なえる。
| パイロット信号を使って伝達路の歪みを推定 |
|---|
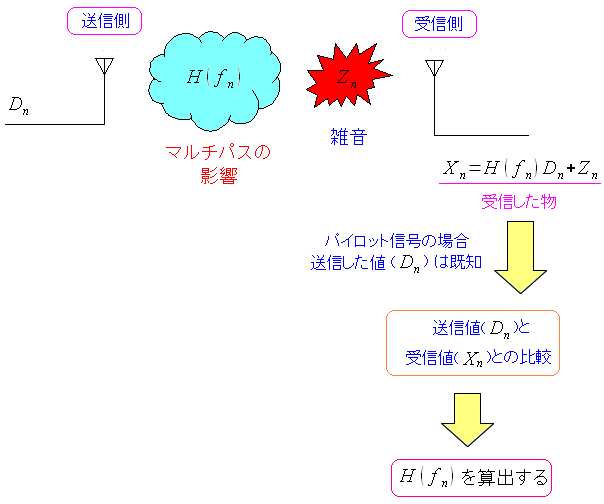 |
|
送信したデータの中身と、受信したデータの中身を比較する事で 伝達路の間で、どれくらいの歪みが生じているのかが推定できるというのだ。 雑音処理はどうしているのか。 資料を探しても見つからなかった。なので、わからんで逃げます! |
マルチパスの種類について
マルチパスといっても、いくつか種類がある。
| マルチパスの種類 | |
|---|---|
| 場所選択性 |
多方向から電波を受信する事で定常波ができ 受信する場所によって受信電力が異なる。 |
| 時間選択性 |
ドップラー効果の影響。 移動体通信(携帯電話など)ではドップラー効果を 考慮する必要はあるが、無線LANでは不要なので 取り上げませんでした。 |
| 周波数選択性 |
今回、取り上げたのが周波数選択性になる。 異なる受信タイミングによって、受信電力が 周波数ごとに変動を受け取る。 |
他にも考慮する項目がある。 直接波と反射波の両方を受信できる環境と 直接波は受信できないが、多方向の反射波を受信できる場合だ。
| 直接波と反射波の両方を受信できる場合 |
|---|
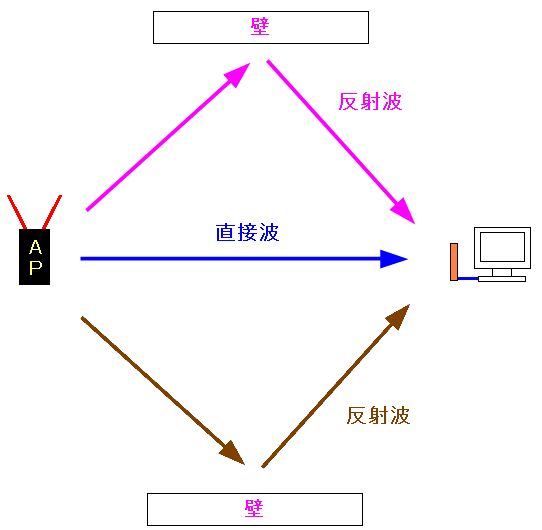 |
| 今まで書いてきた話は、この場合になる。 |
だが、こういう場合もある。
| 直接波は受信できないが、多方向の反射波を受信できる場合 |
|---|
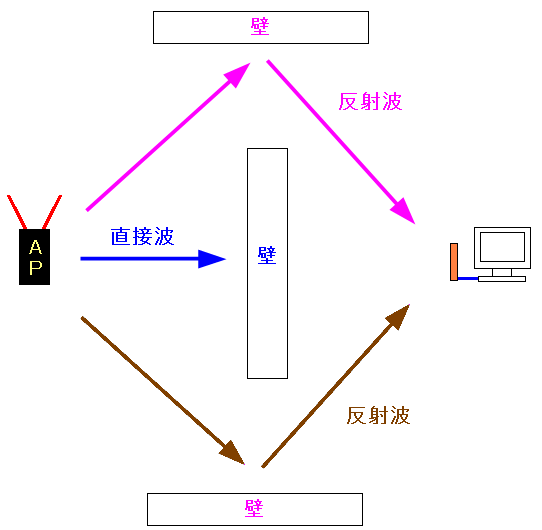 |
|
無線LANでも起こる事がある。 大抵、この話で話題になるのは携帯電話の通信で ビルの谷間での受信など、直接波が入らない場所での パルチパス問題が議論になる。 |
直接波が受信できず、反射波の場合だと、受信波の振幅が どうなるのか、以下の図のようになる。
| 受信波の振幅度合の確率分布 |
|---|
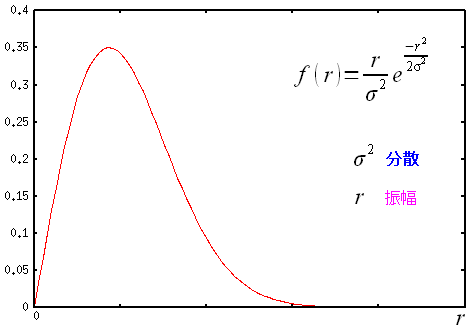 |
| レイリー分布という形で、振幅の度合の確率が出てくる。 |
無線LANでも別の部屋で受信する場合、直接波は受信できなくても 反射波や回折波を受信する事はあるのだが・・・ そこまで調べる気力はあらへん!! という事で、あっさりと挫折するのだった。OFDMでの同期の取りかた
送信側と受信側との間で、どうやって同期をとるのか? 資料を見ると ガードインターバルを使う だった。 資料を見ても・・・ 踏み込んだ所まで理解できへん だった。 そこで概略だけ説明して逃げる事にした。
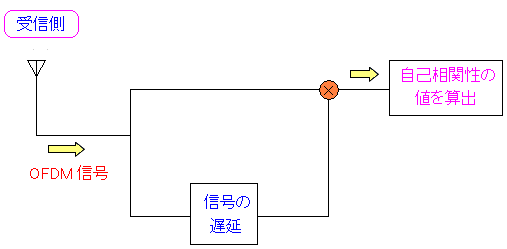
| OFDMでの同期の取りかた |
|---|
 |
|
受信波と受信波を遅延させた物を生成し この2つを重ね合わせて、自己相関関数の値を求める。 |
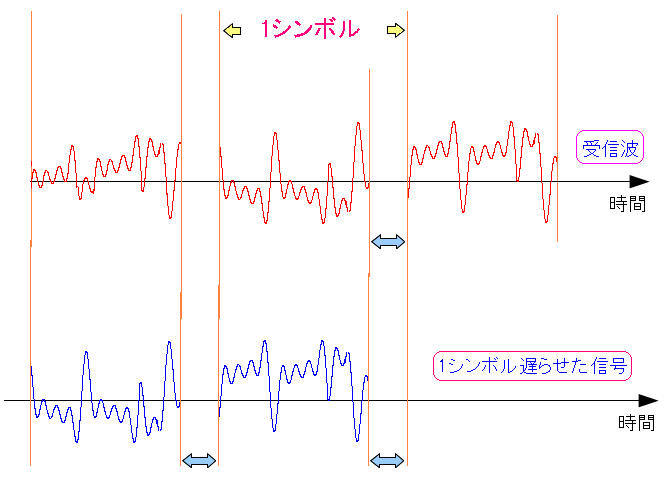
受信波を遅延させた際、丁度、1シンボルだけ遅延したとする。
| 受信波と、受信波を1シンボルだけ遅延させた物 |
|---|
 |
|
ガードインターバル(GI)部分以外は、別々の値になっている。 この場合、GIに雑音が入っていない状態なのだが。 |
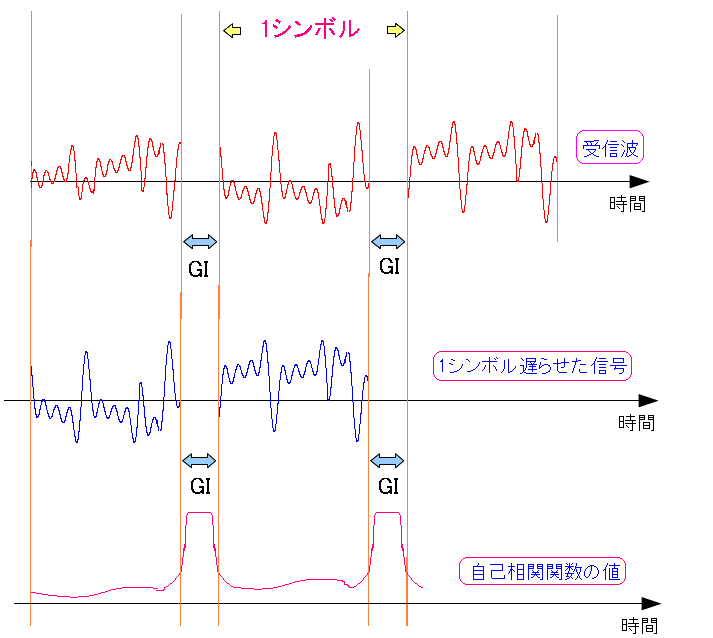
この時の自己相関関数の値は以下のようなると予想できる。
| 自己相関関数の値 |
|---|
 |
|
GIの部分だけ自己相関関数の値が高くなる。 そのため、GIの場所や、GIの開始場所が特定できるのだ。 もちろん、雑音などを考慮すると、ガードインターバルの部分は 値が低くなったりするため、複数の山になっている所の 平均値を出したりするという。 |
というわけで、私自身、大雑把にしか理解できなかったので この辺で逃げます (^^)MIMO
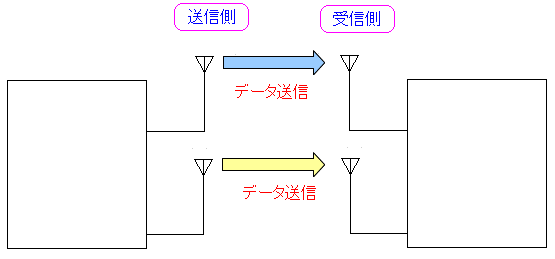
11nから導入された技術としてMIMO(マイモ)がある。 ところでMIMOとは・・・ Multi Input Multi Outputの略 なのだ。 複数のアンテナでデータ送信し、複数のアンテナで受信する事で 大量データやりとりできるようにする技術だ。
| MIMOとは |
|---|
 |
|
上記のように複数アンテナから、同時に複数帯域の搬送波を送信する事で 一度に送信できるデータ量を増加させるための技術だ。 上図の場合、2つの周波数帯域の搬送波を、それぞれのアンテナから送信し 2倍の速度を実現させている。 |
だが、MIMOを実現させるためには、色々な技術が必要だという。 そこで資料を見る。
| 直接波を見るだけでも |
|---|
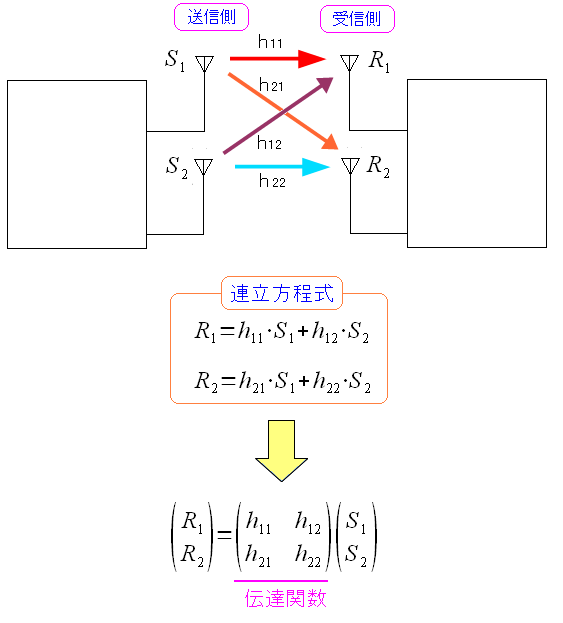 |
|
上図を見ると、送信波は四方八方に飛ぶため、直接波でも 受け手の2つのアンテナで受信する。 そのため2つの直進波を受信する事になる。 もし、伝送路において雑音がない場合は、上図の式になる。 |
もし、雑音を考慮したら以下のようになる。
| 雑音を考慮した場合 |
|---|
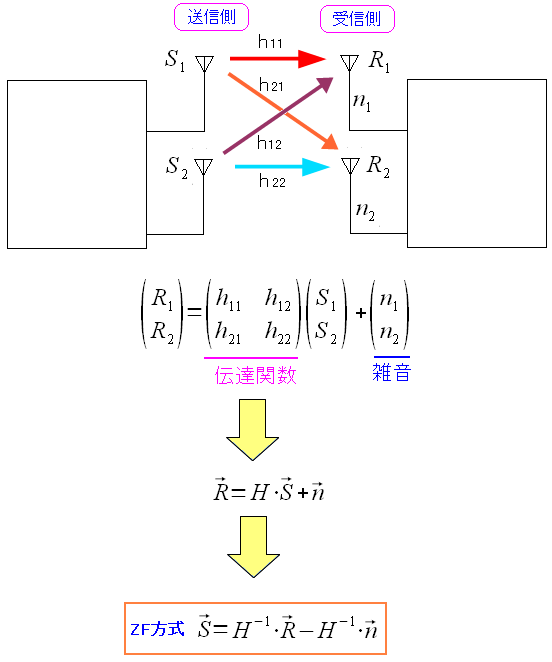 |
| 雑音を考慮した場合、いかに雑音の影響を少なくするかが課題になる。 |
ZF基準だと、伝送路の影響が小さいと、雑音の影響が大きくなる。 そこで、雑音の影響を小さくしたのが MMSE基準 なのだ。 ZF基準といい、MMSE基準といい、信号星座図の補正に使っている物だ。 考え方は、全く一緒なのだ。 他にも 最尤検出(MLD)方式 というのがあるという。 だが・・・ 理解する気が起こらへん! という事で、MIMOの話は、さっさと終わらせる事にした。 でも、終わる前に、最後に、もう1つMIMOの利点を紹介。 IEEE802.11nの実力【技術編】 - 第8回:複数波を合成して信号を安定させる(日経ITpro) マルチパスの影響で、周波数帯域で落ち込む場所が出る事がある。
| マルチパスによる落ち込みが起こる |
|---|
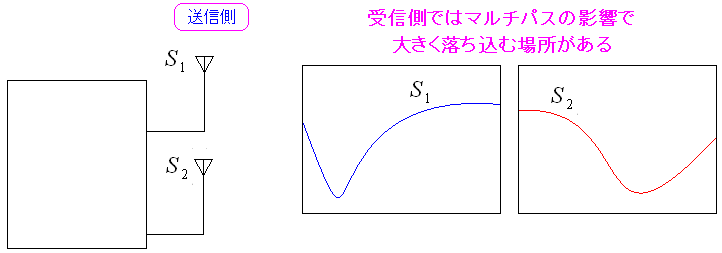 |
|
マルチパスによる、ある周波数帯域での落ち込みが起こる場合がある。 もし、2つ電波を飛ばしていたら、個々に落ち込み場所が異なる事がある。 |
そんな時は、合成する事で、落ち込みを埋め合わせる事ができる。
| 合成波を使う事で |
|---|
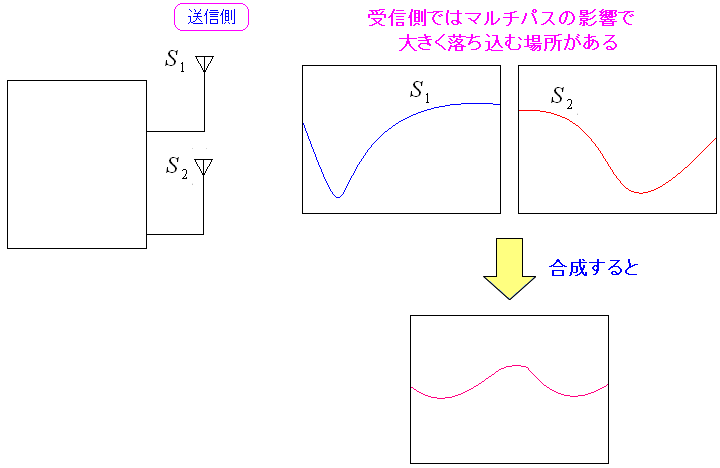 |
| 合成波を使う事で、目立った落ち込みを埋め合わせる事ができる。 |
これがMIMOの利点だ。
直交関数について
デジタル信号処理の話では、三角関数の直交性が出てくる。
| 三角関数の直交性の関係式 |
|---|
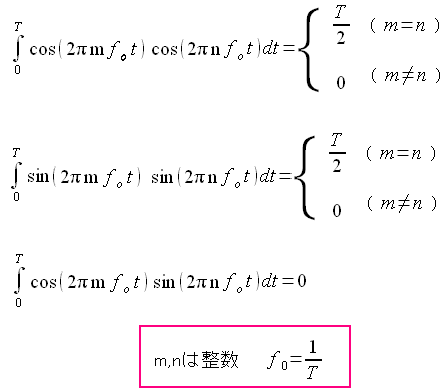 |
|
基本周波数foで、周波数がFoの時の周期がTの場合に成り立つ関係式だ。 必要な周波数を取り出したりする際に使われる。 |
同じ区間の2つの関数を掛け合わせて積分すると「0」になる場合、
まるでベクトルのように直交しているため、直交関数という。
ふーんと思ったのだが、昔、こんな事を見た事がある。
関数もベクトル!
だが、当時、その意味を全く理解できなかった。
そして、そのまま放置していた。
だが、今回の無線LANを調べているうちに以下の資料を発見した。
デジタル情報処理 直交関数展開(大阪大学・医学部)
医学部でも画像処理関係の知識が必要なため
画像処理に必要な数学を教えているようだ。
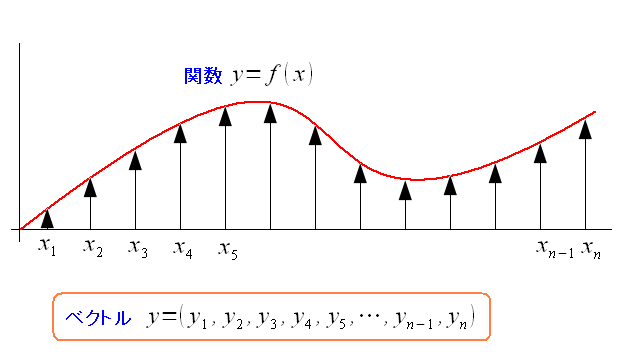
阪大の資料を見ると、関数を以下のように考えるという。
| 関数をベクトルとして見る |
|---|
 |
|
y=f(x)の関数で、個々のyの値を成分とした物を ベクトルとして考える。 |
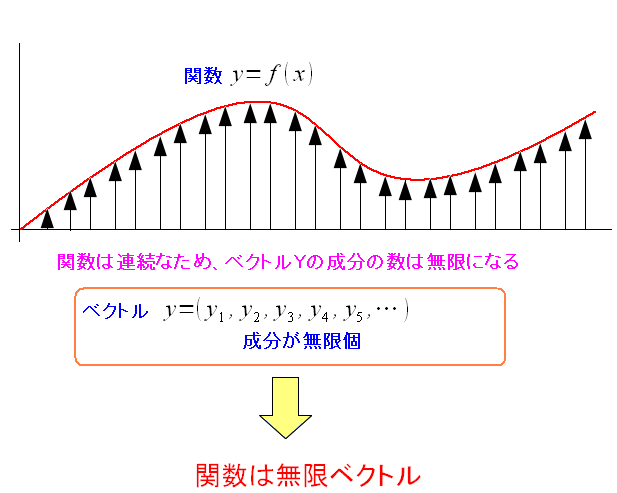
もっとx軸上の各点の間隔を縮めてみる。
| 無限ベクトルになる |
|---|
 |
|
x軸は連続なので無限に区切る事ができる。 そして各yの値も無限個存在する。 関数は成分が無限個ある無限ベクトルといえる。 |
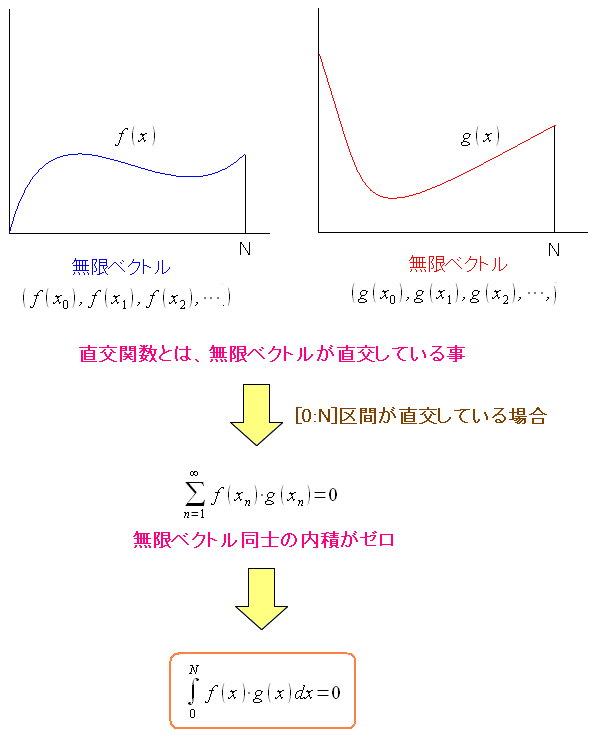
関数の直交性とは何か。 次のような事だったのだ。
| 関数の直交性とは |
|---|
 |
|
[0:N]区間でのy=f(x)とy=g(x)の関数を考えてみる。 2つのベクトルが直交している場合、内積は「0」になる。 お互いの独立しているからだ。 関数の無限ベクトルの場合も、内積のf(x)・g(x)が値が「0」になる 無限個あるので、積分を使って表現する事ができる。 これが関数の直交性だ。 |
フーリエ展開で考えると、わかりやすくなる。 フーリエ展開とは、どんな関数も三角関数で表現できる。
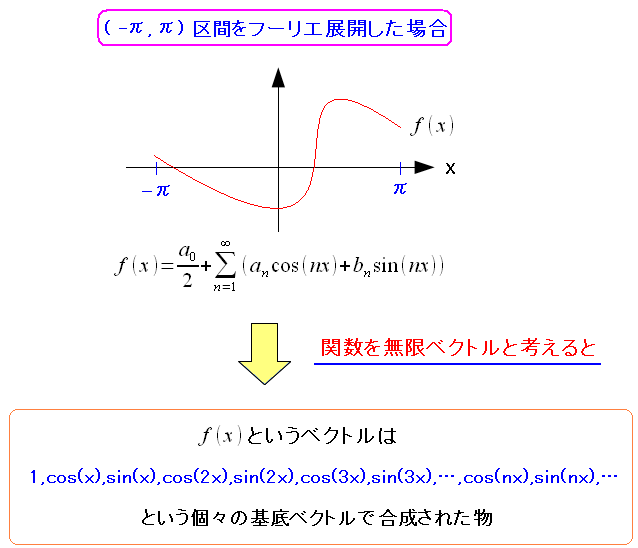
| フーリエ展開と関数の直交性 |
|---|
 |
|
[-π,π]の範囲での関数の無限ベクトルだ。 上図のように1,cos(x),sin(x),…を基底ベクトルとした 合成ベクトルがf(x)の関数になる。 |
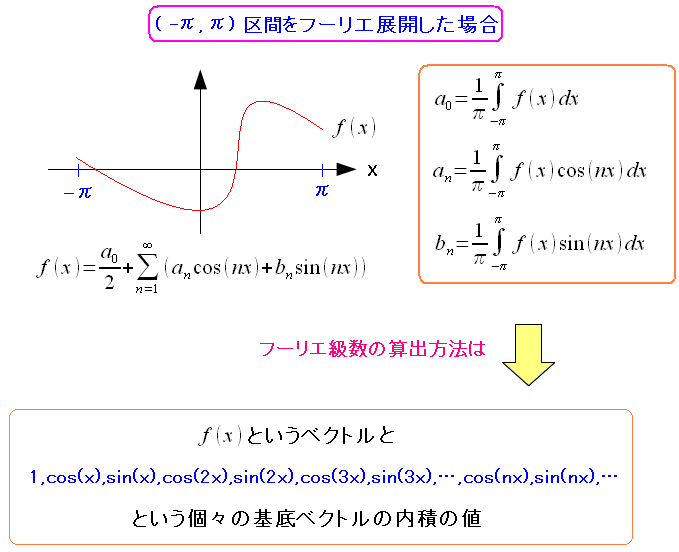
フーリエ展開を各・無限ベクトルの分解と見ると、見通しが良くなる。 フーリエ級数の意味は以下のようになる。
| フーリエ級数の意味 |
|---|
 |
|
フーリエ級数の算出だが、内積の値を求めている事になる。 どの成分が、どれだけf(x)の合成に関係しているかを表している。 |
改めて思った。 内積とはお互いの類似の度合 であり 依存度や構成の度合 なのだ。 だから・・・ 相関関数の相関の度合が内積の値になる というのも納得できる。 ところで阪大の資料には、多項式の直交性にも触れていた。 ル・ジャンドル多項式 なのだ。 昔、習ったような気がする。 20世紀の事なので、記憶は確かではない。 どんな物か見てみる事にした。
| ルジャンドル多項式 |
|---|
 |
| [-1:1]の区間で、直交している多項式だ。 |
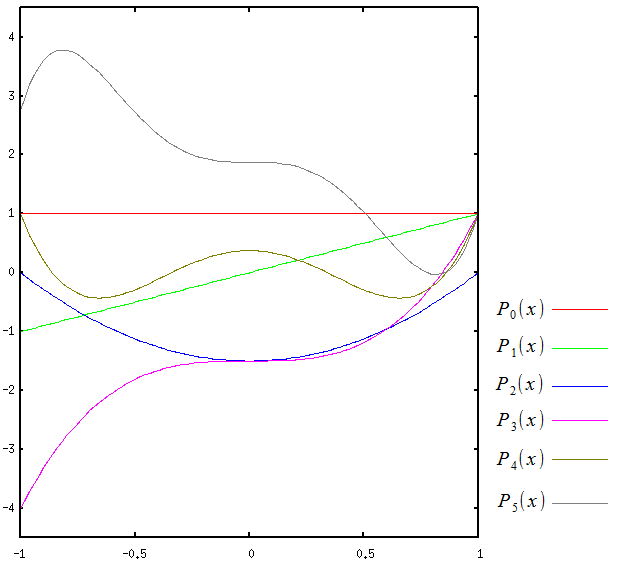
これをグラフにすると、以下のようになる。
| ルジャンドル多項式をグラフにしてみた |
|---|
 |
|
関数や多項式の場合、見た目では直交の有無はわからないが お互いが独立しているため、直交している事になる。 |
ところで・・・ ルジャンドル多項式は何に使われるねん? という事で調べてみる。 すると・・・ 量子力学で出てくる ようだ。 だが、量子力学のどういった所で使われているかといえば わかるわけないだろ!!! 私が理系だったのは20世紀。 21世紀で、未来志向のため、今や理系の意地は全くないので あっさりと「わからん」で逃げてしまう私。 大阪大学の資料のお蔭で、長年の謎が解けただけでなく デジタル画像処理の話にも興味を持つようになった。
デジタル信号と誤り率について
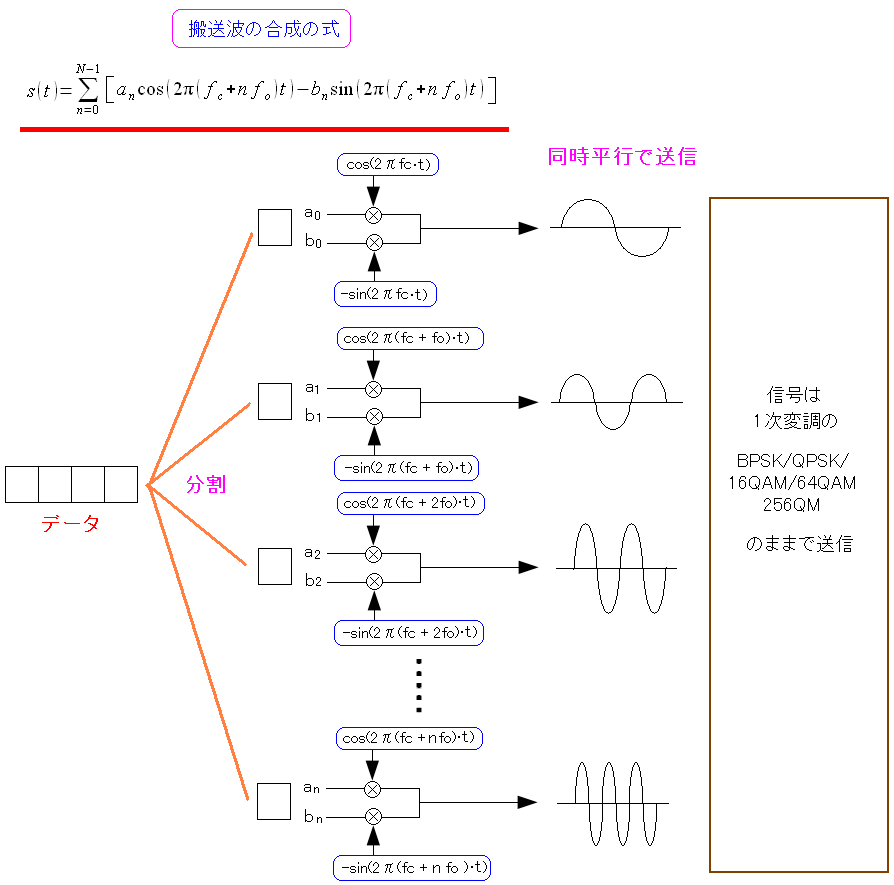
直接拡散方式では、デジタル信号の誤り率の話が出てこないのに OFDM変調だと、誤り率の話が出てくる。 なぜか不思議に思ったのだが、ある事に気づいた。 OFDM変調は、信号を加工してへん!! なのだ。 確かに直接拡散の場合、一次変調でBPSKかQPSKに変調し その後、PN符号で拡散を行なっている。 だが、OFDMではデジタル信号を分割しているものの 1次変調した信号を、さらに加工しているわけではないのだ。
| OFDMだと1次変調したデータは加工していない |
|---|
 |
|
OFDMの場合、デジタル信号を分割し、1次変調(BPSK、QPSK、16QAM、64QAM、256QAM)を 行なっている。だが、1次変調を行なったデータを、更に加工する事はしていない。 |
1次変調したデータが、そのまま雑音やマルチパスの影響がある中を 送信するため・・・ 誤り率が重要 になってくる。デジタル通信と誤り率の算出について
デジタルは「0」と「1」の信号だが、1次変調の際 BPSKでも、QPSKでもQAMでも、正弦波という形で送信される。 電波が通る空間中には雑音がある。 雑音の影響で「1」を「0」と判定したり、その逆もある。 ところで、誤り率を計算する場合、雑音は 白色ガウス雑音 を使うという。 白色ガウス雑音って何やねん? なのだ。 そこで調べてみる事にした。 不規則で、ガウス分布に従う雑音 だという。 ガウス分布。高校の統計で出てきた。 以下の分布の事を言うのだ。
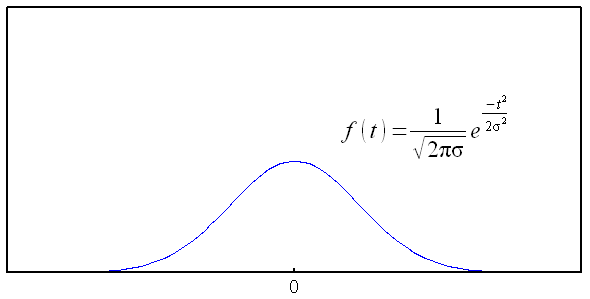
| ガウス分布 |
|---|
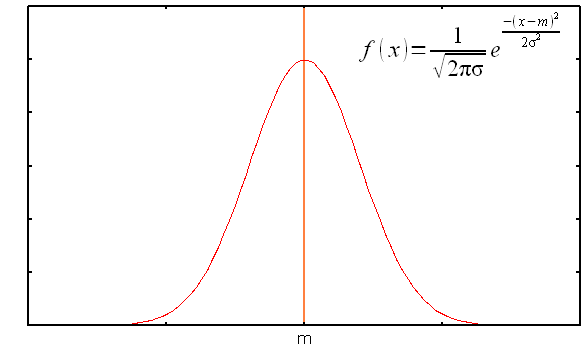 |
|
一般式とグラフを描いてみた。 綺麗な山を描くような形をしている。 σは、裾の広がり度合を表す。 |
| ガウス分布 |
|---|
 |
|
一般式とグラフを描いてみた。 綺麗な山を描くような形をしている。 σは、裾の広がり度合を表す。 |
0を中心とするガウス分布は以下のようになる。
| 0を中心とするガウス分布 |
|---|
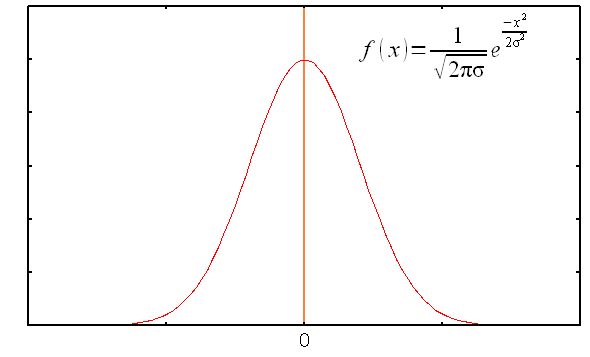 |
|
綺麗な山を描くような形をしている。 σは、裾の広がり度合を表す。 雑音の分布は、0を中心としたガウス分布に従うという。 |
簡単にガウス分布の説明をした所で、データ送信の際の 誤り率の算出方法が、どうなっているのか調べてみた。 BPSK変調の場合の誤り率の資料を発見した。 10.デジタル変復調と誤り率特性(大分大学) まずはBPSK変調のおさらいから。
| BPSK変調 |
|---|
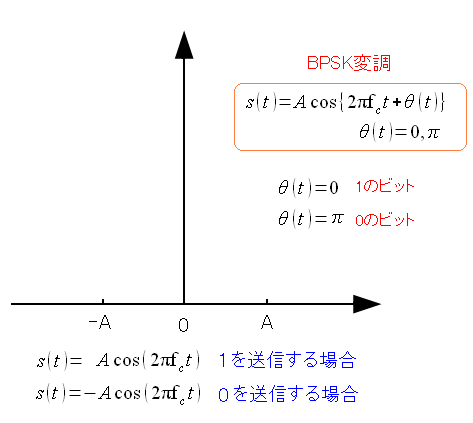 |
|
余弦波で信号を伝えるのだが、「0」と「1」の違いは 位相のズレで判断させている。BPSKの場合、180度のズレを使っている。 |
BPSK変調をした後で、雑音がある空間中に、電波を送信し 受信側で、どう検出されるのかを、資料の真似をしながら 計算してみる事にした。
| BPSK変調で雑音がある空間中を送信させてみる (同期検波の場合) |
|---|
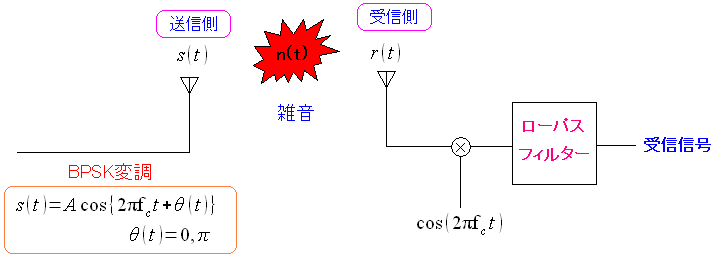 |
|
受信側には復調の際に必要な、余弦波を掛け合わせる部分や ローパスフィルター(LPF)が用意されている。 信号処理後、変位値「-A」か「A」を容易に取り出せるようにしている。 |
送信した電波を受信した。 その時、受信波がどうなっているのか。
| 受信波について |
|---|
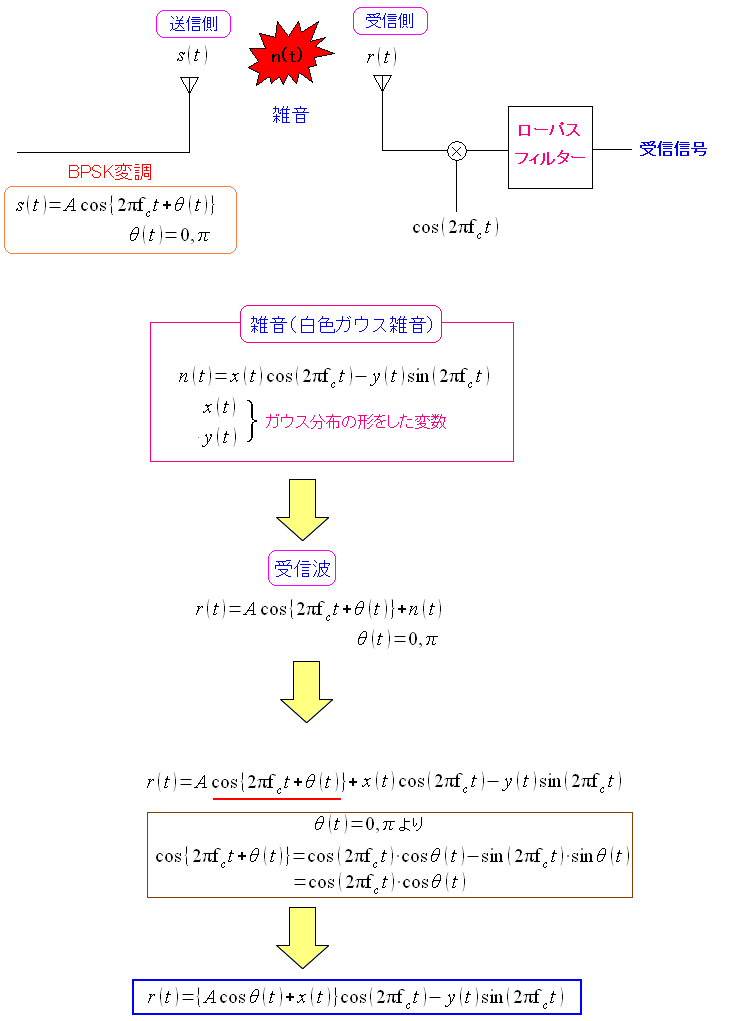 |
|
雑音は白色ガウス雑音で、ガウス分布に従っている。 それが空間中に、送信波と合成され、受信側にとらえられる。 |
受信した信号を復調するために、加工する必要がある。 それが余弦波を掛け合わせて、ローパスフィルター(LPF)を通す処理だ。
| 受信波の加工処理 |
|---|
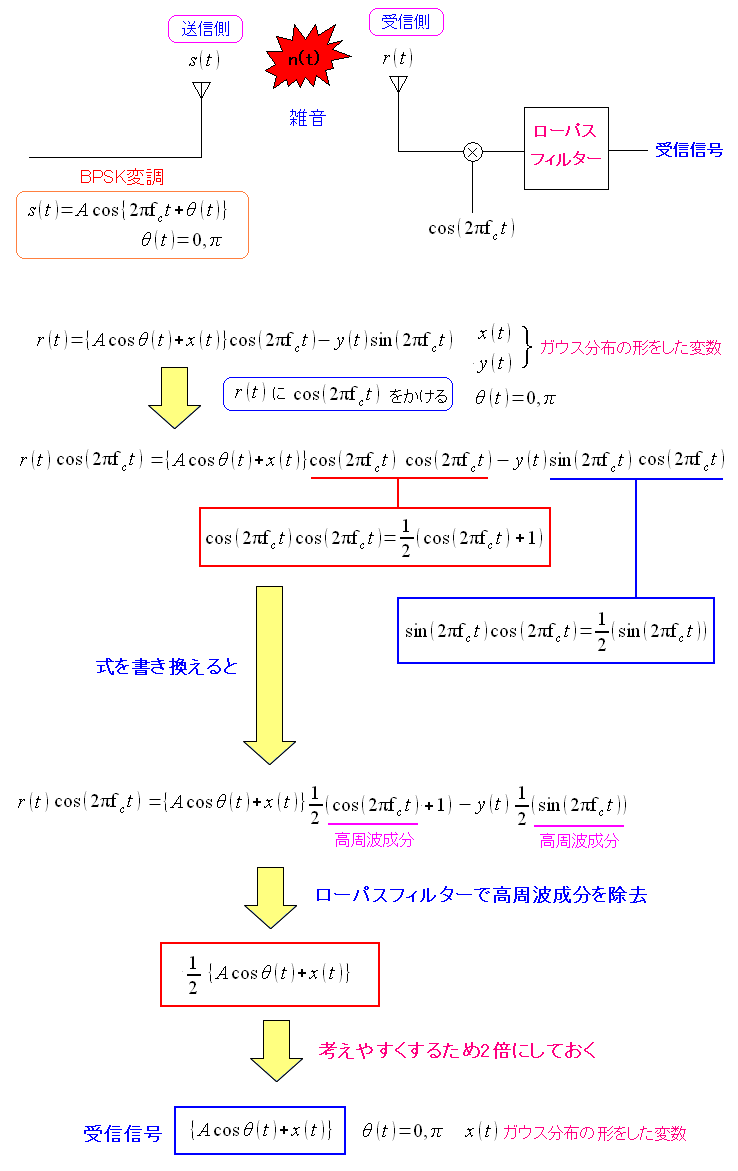 |
|
BPSK変調では、雑音がない状態で、余弦波を掛け合わせて ローパスフィルター(LPF)を通すと、変位の値(-AかA)を取り出せる。 雑音が混ざると、変位の値と雑音の合成値が取り出せる。 |
雑音はガウス分布に従うという前提で考える。
| 雑音がある場合、信号受信の値に誤差が発生する |
|---|
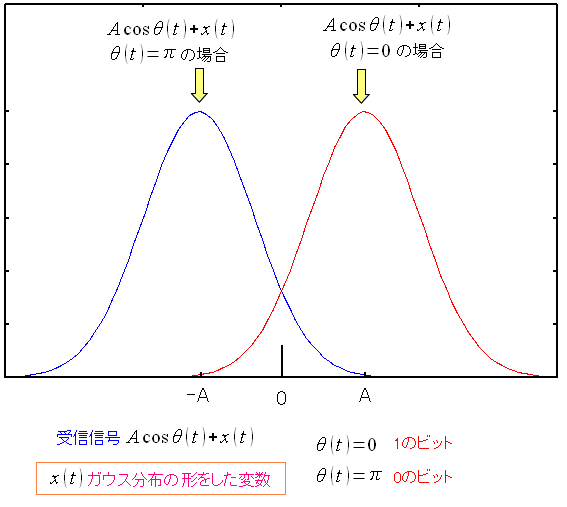 |
|
受信した変位「-A」の信号に雑音を混ぜた時、どの値をとるかの確率分布と 受信した変位「A」の信号に雑音を混ぜた時の値の、確率分布を表している |
雑音が大きい場合、閾値(しきい値)の「0」を越えるため誤判定が起こってしまう。
| 雑音が大きいと閾値を越えてしまう |
|---|
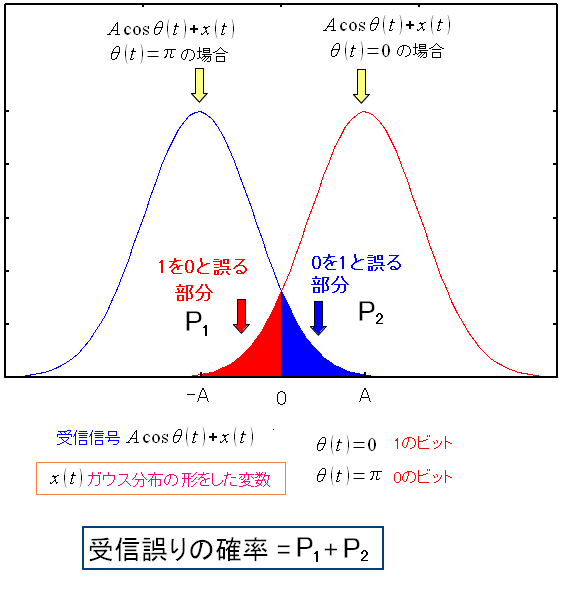 |
|
「0」を閾値(しきい値)にしているが、雑音が大きい場合だと 閾値を越えてしまうため、誤判定をしてしまう事が確率的に起こってしまう。 ビット誤りの確率は「0」を「1」と判定してしまう確率と 「1」を「0」と判定してしまう確率の合計になる。 |
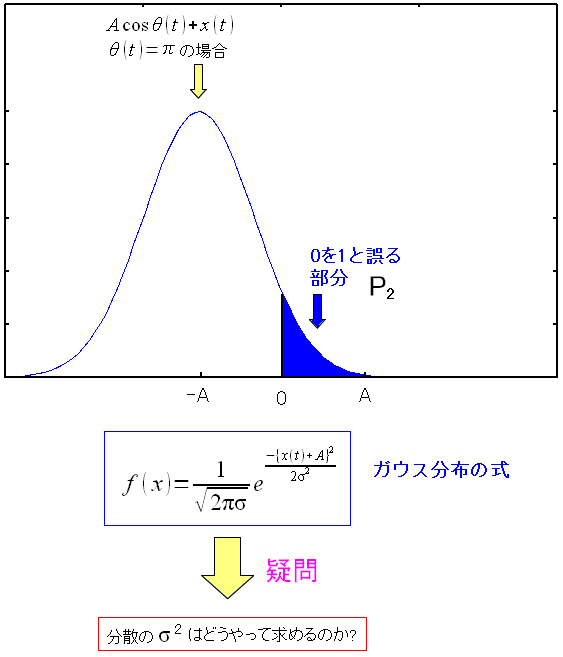
ところで雑音がガウス分布に従うという話なのだが
分散のσ^2は、何になるねん?
と思った。
| 分散σ^2は何に当たるのか? |
|---|
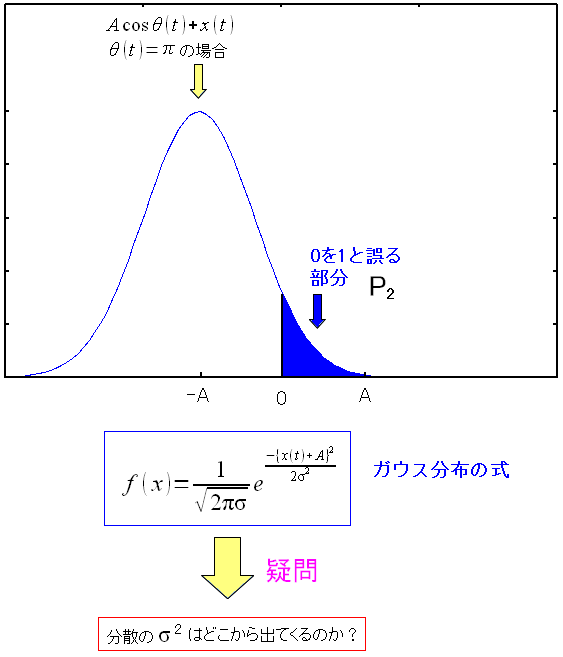 |
|
白色雑音がガウス分布に従うといっても、分散は何なのか気になった。 ガウス分布で分散は裾野の広がり具合を意味するのだが それだけでは抽象的すぎて、全くわからないし その後の式の展開を見ても、チンプンカンプンになってしまう。 |
そこでガウス分布のおさらいをする事にした。
| 分散とは |
|---|
 |
|
分散とは、真値と観測値の差の2乗の平均値だ。 真値がわからない場合は、平均値と観測値の差の2乗の平均値を取る。 |
| この場合の分散とは |
|---|
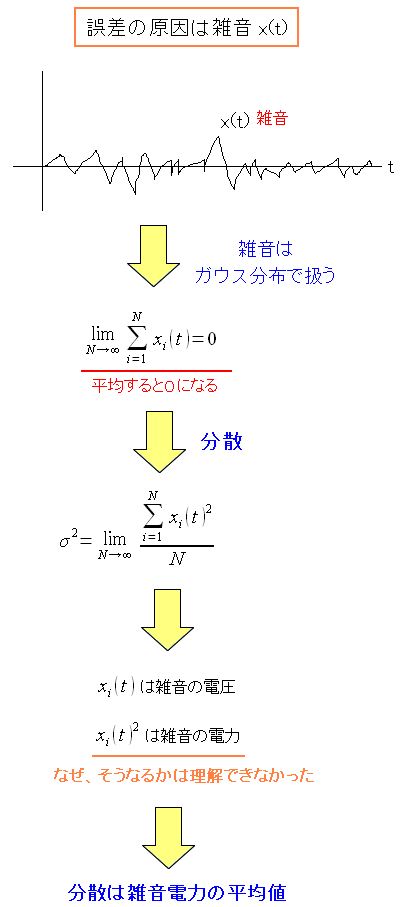 |
|
雑音は0を中心に不規則にジグザグしている。 だが、平均すると0になる。 各観測地点でのx(t)の値の2乗は、雑音電力になる。 そのため分散は、雑音電力の平均値になるのだ。 ところでx(t)の2乗が雑音電力になる理由を調べた。 だが、私の頭では理解できなかったので・・・ 謎のままにするのだ!! という事で理解するのを諦める事にした。 |
分散が雑音電力(平均電力)だというのがわかった。 さて、雑音の影響による誤判定の確率の話に進む事にする。
| 誤判定する確率(1) |
|---|
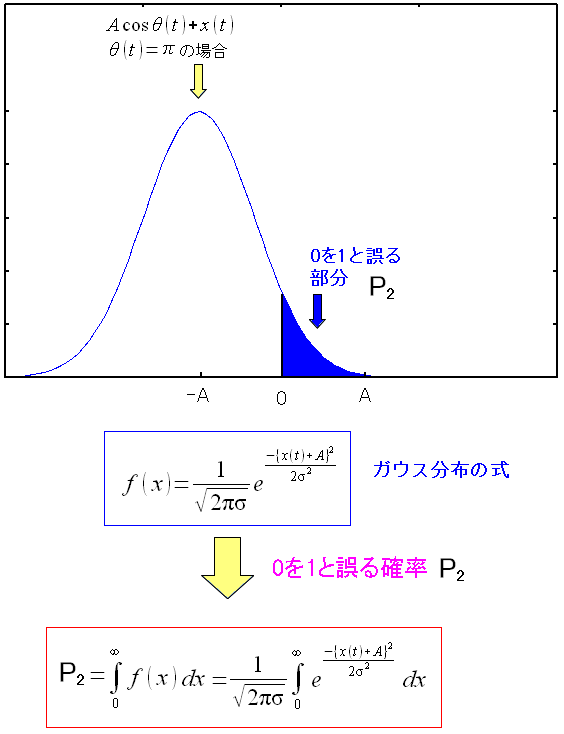 |
|
「0」を「1」と誤判定する確率をP2とする。 式では上にある通りだ。 |
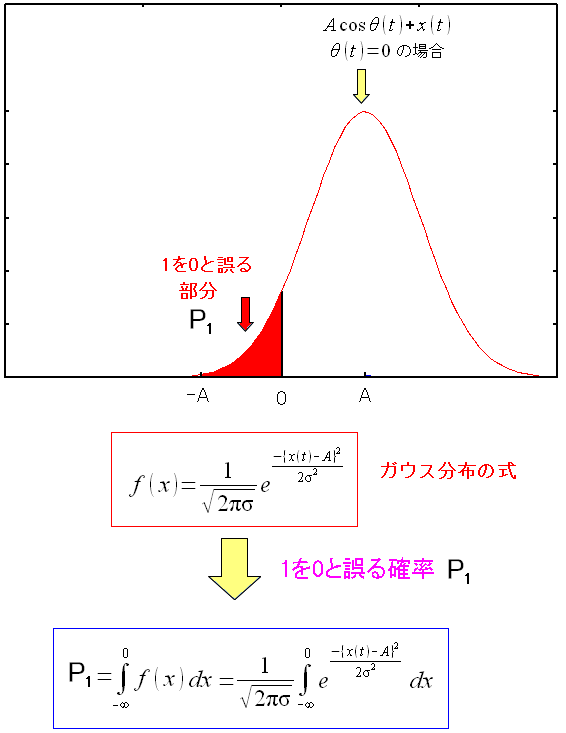
今度は、「1」を「0」と誤判定する確率を求めてみる。
| 誤判定する確率(2) |
|---|
 |
|
「1」を「0」と誤判定する確率をP1とする。 式では上にある通りだ。 |
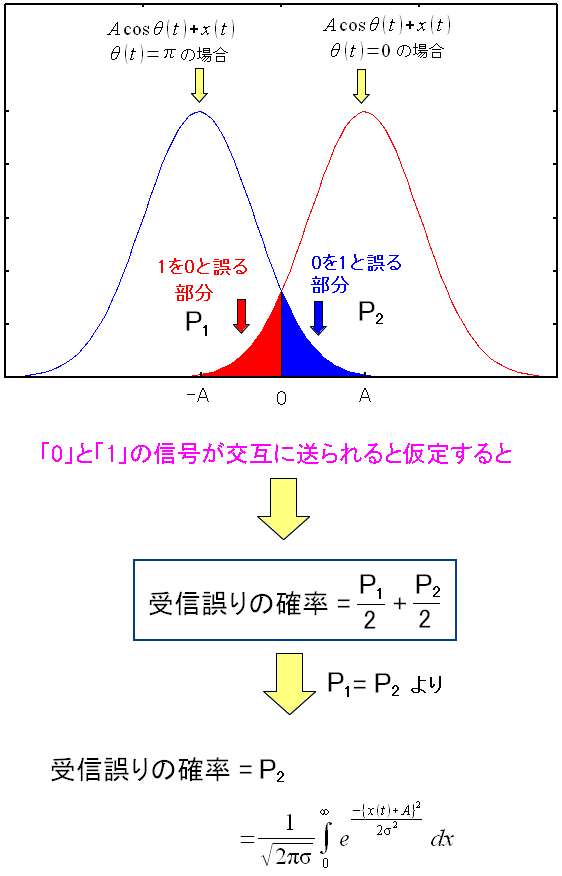
そこでBPSK変調で雑音のために誤判定する確率を求めてみた。
| BPSK変調で雑音の影響で誤判定する確率 |
|---|
 |
|
上図のように計算できる。 雑音の影響による誤判定の確率を求める式が導けた。 と偉そうに書きながら、実は資料の丸写しなのだ。 |
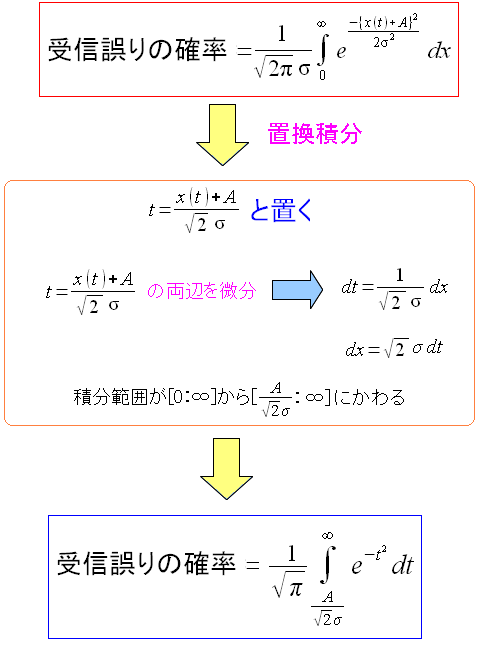
次に式を以下のように書き換えるという。
| 誤判定の確率式の書き換え |
|---|
 |
|
ガウス分布で求めた誤判定の式を、上のように展開するという。 途中、置換積分を行なう。20世紀以来だ。 書き換えた数式は誤差関数という。 |
ふと高校時代の数学の先生の言葉を思い出した。 チカン積分だからといって痴漢ではないで 高校生だった当時 先生、寒い!! と思ったが、不惑になった今では、連発しそうなネタだ。 さてさて誤差関数とは何か。
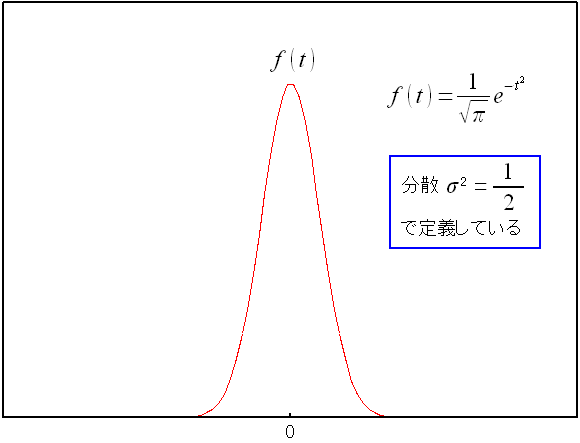
| 誤差関数とは |
|---|
 |
|
誤差関数とは分散σ^2を0.5にしたガウス分布だ。 ガウス分布の特殊形(?)になる。 全範囲を積分したら「1」になる |
一般的なガウス分布は、裾野の広がりを持っている。
| 一般的なガウス分布 |
|---|
 |
| 分散の度合を考慮したガウス分布になる。 |
ところで 誤差関数に置き換える理由は何やねん? と思った。 資料をみると erf()関数 と書いている。 そこで思った。 エクセルやcalc、gnuplotでも使える関数だろうか? だった。 そこで調べてみると、案の定、使える関数だった。
| erf()関数 |
|---|
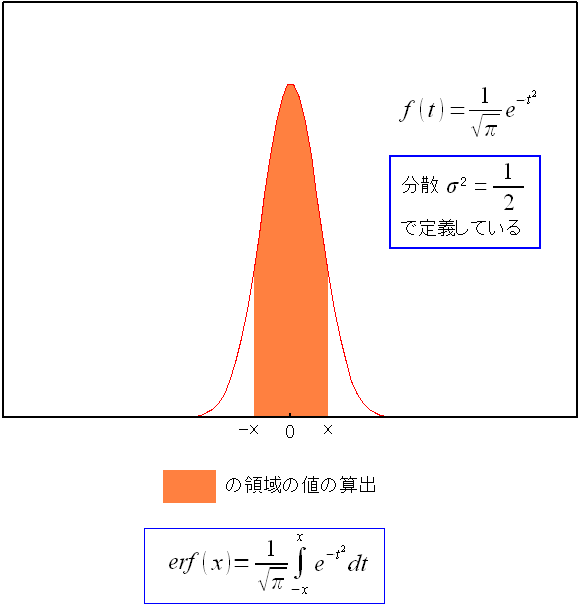 |
| 誤差関数で区間[-x:x]に収まる確率(積分値)になる。 |
そして誤差関数以外の領域(両側の領域)の入る確率が
相補誤差補関数 erfc()なのだ。
| 相補誤差補関数 erfc() |
|---|
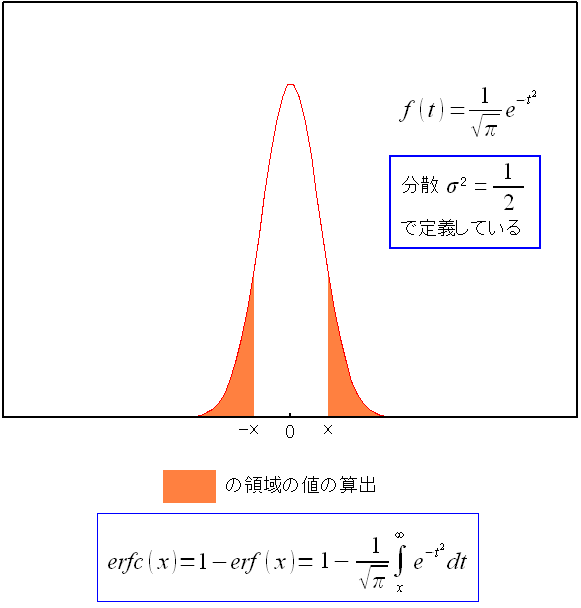 |
| 誤差関数で区間[-x:x]の外になる確率(積分値)だ。 |
誤差関数erf()も、相補誤差関数erfc()も・・・
エクセル、calc、gnuplotでも使える!
のだ。
そこで文明の利器を使う事にした。
| 受信誤りの確率をerf()関数で表す |
|---|
 |
| 受信誤りの確率の式をerfc()関数で表せた。 |
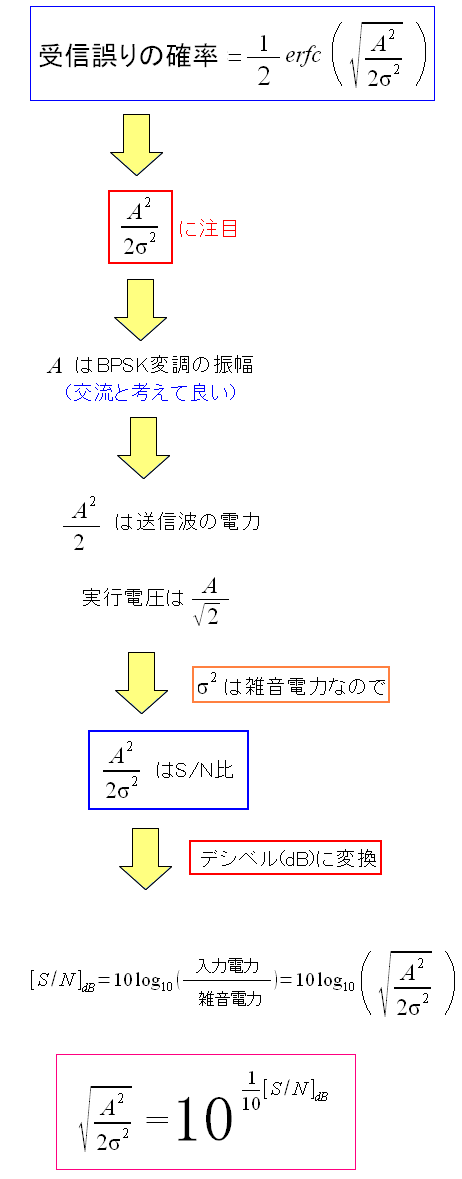
次にerfc()関数の中の変数を見てみる。
| erfc()関数の中の変数 |
|---|
 |
|
関数の中に入る変数は、入力電力と雑音電力の比だ。 その比率をデシベル(dB)で表す事ができる。 |
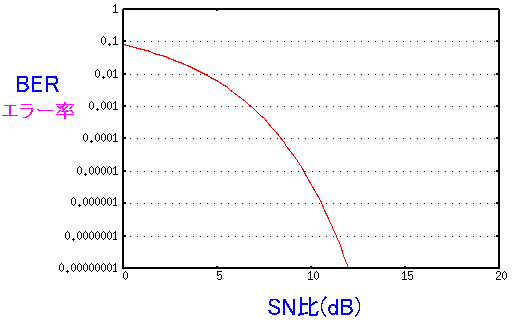
早速、erfc()関数を使って、gnuplotでグラフにしてみた。
| erfc()関数を使って、グラフにしてみた |
|---|
 |
|
S/N比の値と、ビット誤り率のグラフが描けた。 雑音が小さい、もしくは入力信号が大きいとビット誤りが下がる。 |
QPSKの場合のビット誤り率(BER)
BPSK変調の場合のビット誤り率の式が導けた。 次にQPSK変調についても見てみる事にした。 QPSK変調での、ビット誤り率の式を導いた資料を発見した。 2011年後期 通信伝送工学 第12回 QPSKの変復調(東京工業大学) 搬送波デジタル通信 多相変調(信州大学)
| QPSKの信号星座図 |
|---|
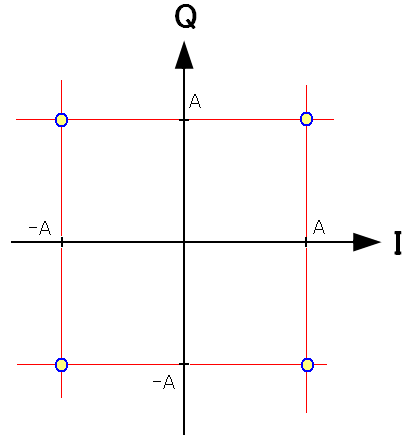 |
| 4つの点で2bitの信号を表現している。 |
ところで、雑音により、受信信号がズレた位置に来るため 誤判定が起こり得る。 受信信号の判定を行なう閾値(しきい値)を以下にようにするという。
| 受信信号の判定を行なう閾値(しきい値) |
|---|
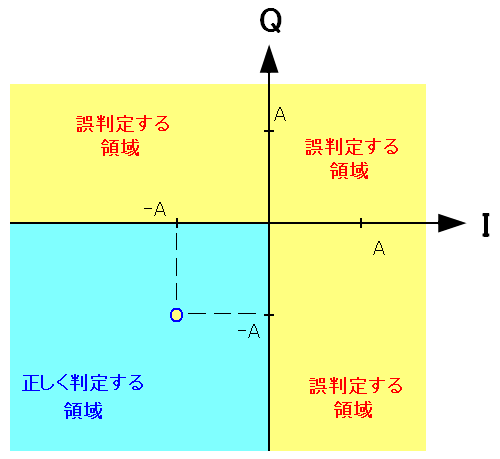 |
|
第三象限の信号について考えてみる。 受信した信号の座標が第三象限内に入れば正しく受信 それ以外の領域になれば、誤判定とする。 |
ビットの誤り率の式を求める際、近似計算が使われるという。
| QPSK変調のビットの誤り率の求め方(1) |
|---|
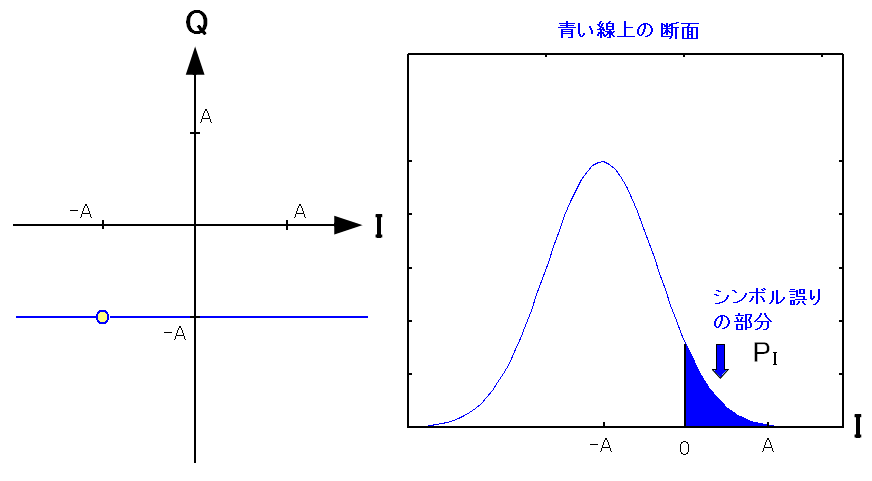 |
|
青い線(I軸方向)の断面をとる。 雑音はガウス分布に従うため、受信した信号の位置の確率も ガウス分布になる。 |
そして次に縦方向(Q軸方向)を見てみる。
| QPSK変調のビットの誤り率の求め方(2) |
|---|
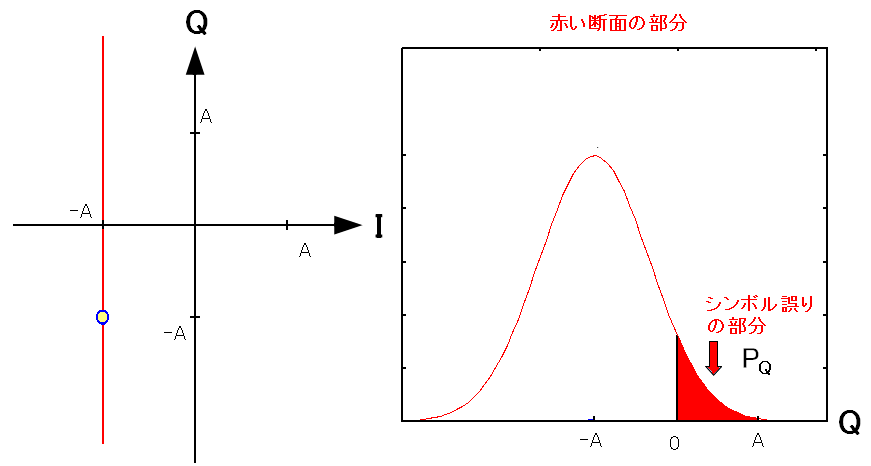 |
|
赤い線(Q軸方向)の断面をとる。 雑音はガウス分布に従うため、受信した信号の位置の確率も ガウス分布になる。 |
そこで以下のように式の展開を行なう。
| QPSK変調のビットの誤り率の近似式の求めかた |
|---|
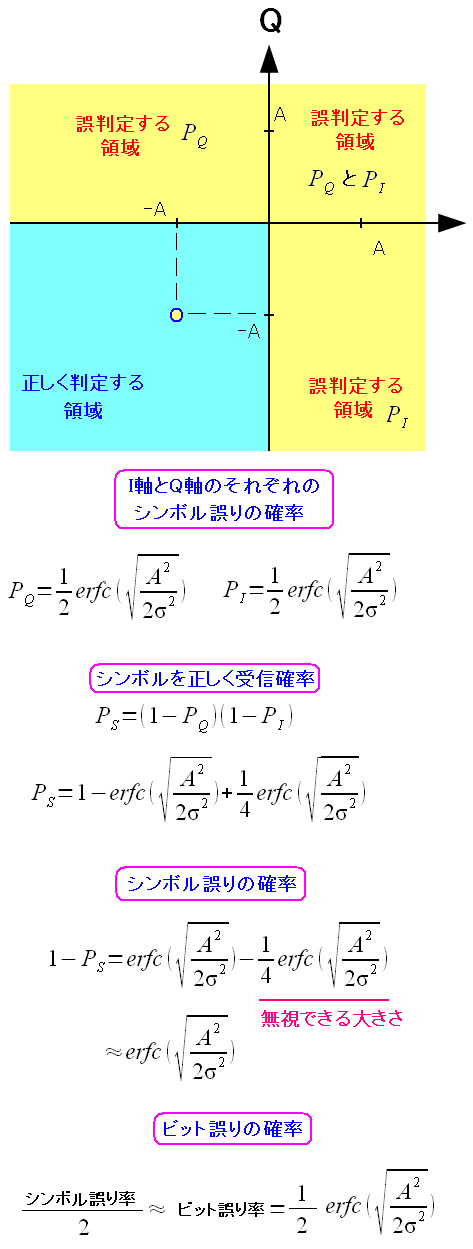 |
|
QPSK変調は、1シンボルで2ビットのデータを送信している。 そのため、シンボル誤り率が求められる。 ビット誤り率は、シンボル誤り率の半分というのだ なぜ、半分なのかは、わからずしまいだった。 (注意) QPSKの場合、非グレイ符号とグレイ符号の違いがある。 それによってビット誤りがシンボル誤りの半分なのか そうでないかが変わってくる。 非グレイ符号、グレイ符号については後述しています。 |
この時・・・ BPSKとQPSKのビット誤り率は同じ! なのだ。16QAMの場合のビット誤り率
16QAMの場合のビット誤り率はどうなのか。 調べてみた。 デジタル変調(電子情報通信学会) ビット誤り率 (BER) - MATLAB & Simulink - MathWorks 日本 正方QAMの厳密なビット誤り率(宇都宮大学) だが・・・ 資料によって式が異なる だった。
| 16QAMの信号星座図とビット誤り率の近似式 |
|---|
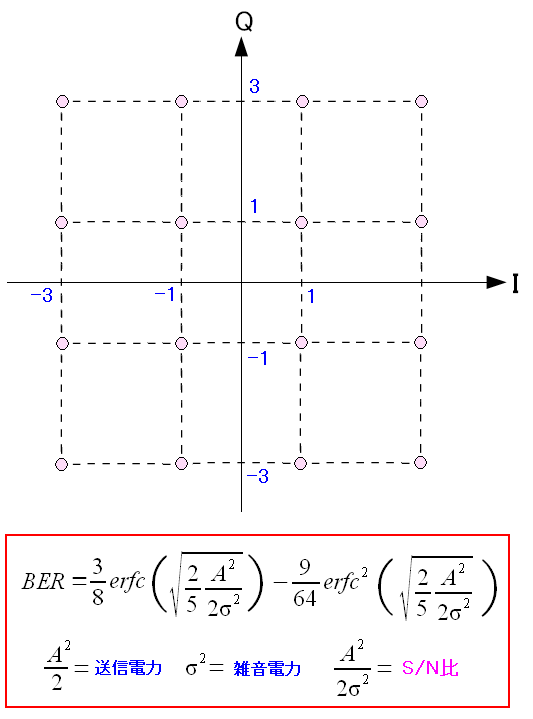 |
|
16QAM変調で電波を飛ばした際、変調方法や伝送路の条件などによって ビット誤り率の式がかわってくるみたいだ。 ここでは、電子情報通信学会の資料に載っていた近似式を載せた。 |
16QAMのビット誤り率の算出の仕方がよくわからない。 でも、ここで立ち止まっても仕方がないので、わからんまま、前に進む。 これをBPSK/QPSKのビット誤り率と比較してみた。
| BPSK/QPSKと16QAMのビット誤り率と比較 |
|---|
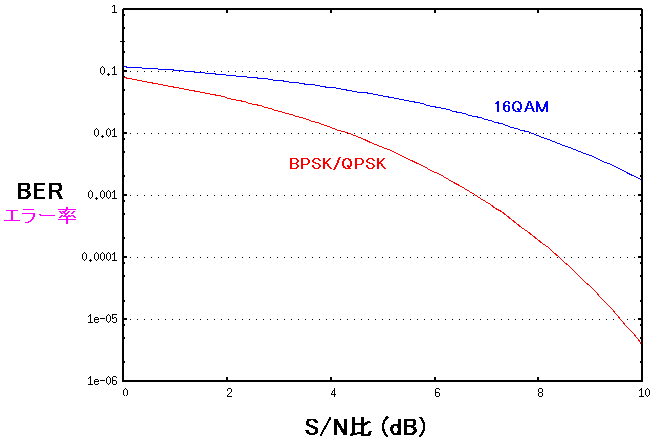 |
|
16QAMの場合、S/N比の値をあげても、ビット誤り率の下がりが悪い。 逆にいえば、通信の際、雑音の影響をできるだけ下げたりする必要が出てくる。 16QAMは1シンボルで4ビットのデータが送れる半面、雑音などに弱くなるのだ。 |
遅延検波 DBPSKの誤り率
ここまでは同期検波のBPSK/QPSKとQAMについて見てみた。 だが、実際の所、BPSKの場合、遅延検波が使われている。 ネットなどで、BPSKとDBPSKとの誤り率のグラフをみても DBPSKの誤り率の算出を調べてみたが・・・ どこにも載ってへん!! だった。 このまま諦めようとしたのだが、往生際の悪さは天下一品なので 自分で導いてみよう! と思った そこで送信波と受信波の式から考えてみた。
| 送信波と受信波 |
|---|
 |
|
送信波は「0」と「1」との違いで、位相が180度ずれる式だ。 伝送中に雑音の影響を受ける。 受信波は、送信波に雑音を足し合わせた物になる。 |
受信波の式ができた所で、検波について考えてみる。
| DBPSKの検波と雑音の影響 |
|---|
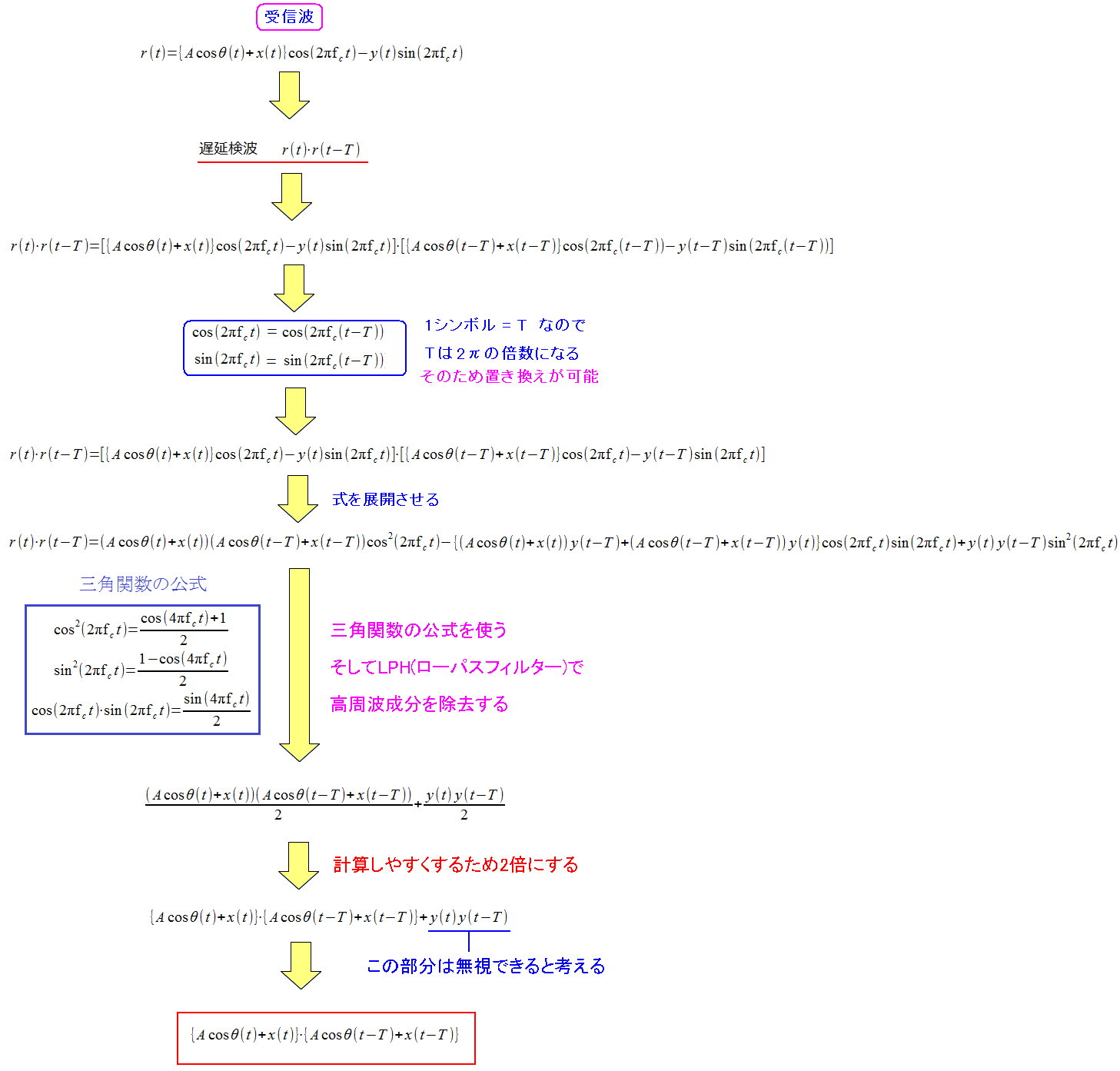 |
|
式を展開していく。 DBPSKは遅延検波なので、同期信号ではなく 1つ後のシンボルと掛け合わせる。 雑音同士、掛け合わせた項は、無視できると考えた。 そして遅延検波の近似値を算出した。 |
そして、どれくらい誤りが発生するのかを考えてみる。
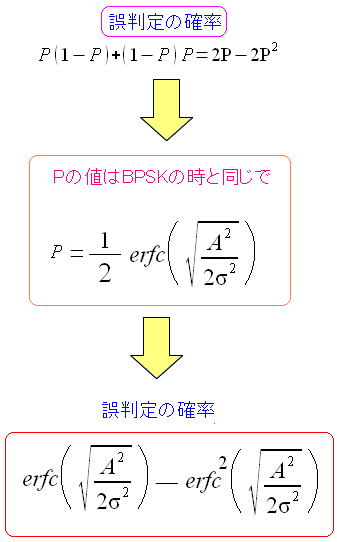
| DBPSKの誤り率の算出 |
|---|
 |
|
受信波と、1つ後の受信波が、共に誤判定された場合 両方とも正しく判定された場合と、同じ値になるため 正しく受信したと判定される。 そのため誤り率の式は上図のようになる。 |
誤り率の式がでてきた。 だが、このままでは使えない。 Pの値として、何が入るのかを決める必要がある。
| DBPSKの誤り率の算出(2) |
|---|
 |
|
受信波が誤判定する確率は、ガウス分布に従う。 そのためPの値は、erfc()関数で算出される この辺りは、BPSKでの誤り率算出と全く同じだ。 |
その結果、DBPSKでの誤り率のグラフが描けた。
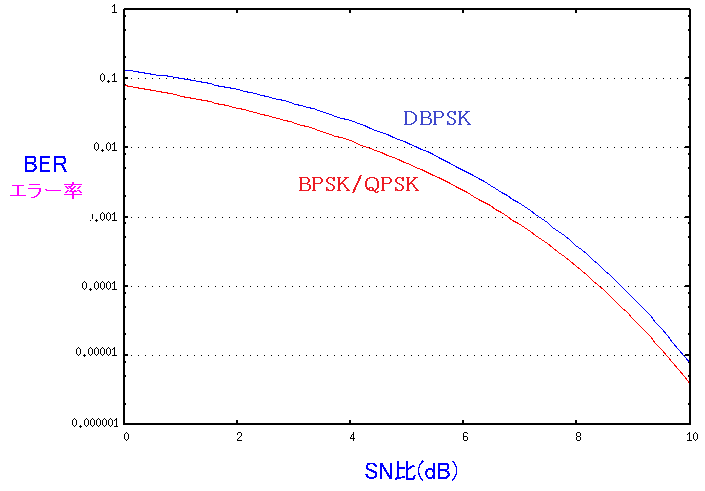
| BPSK/QPSKとDBPSKの誤り率のグラフ |
|---|
 |
|
DBPSKの方が誤り率が高くなっている。 このグラフが正しいのかどうか、ネットに転がっているグラフと見比べたら 同じような結果だった。自分で導いた方法が正しかったので、一安心したのだ。 |
グレイコード (グレイ符号)
誤り率の資料を見ていると、グレイコードという単語が出てきた。 もちろん・・・ それって何やねん? なのだ。 調べてみる事にした。
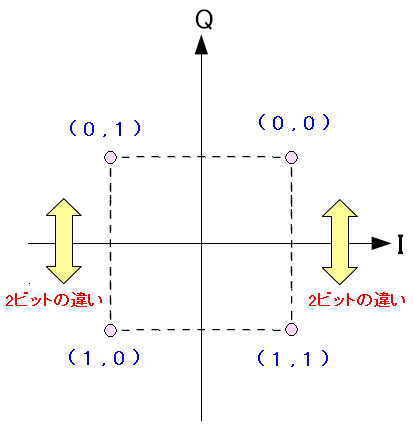
| グレイ符号のQPSKの信号星座図 |
|---|
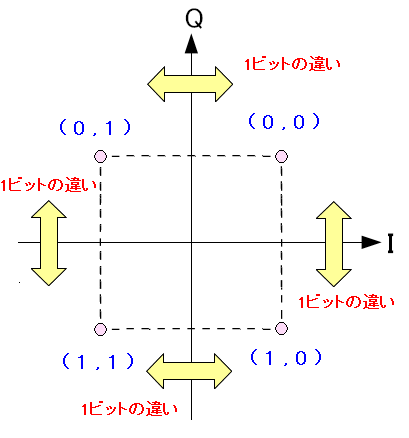 |
| グレイ符号とは、隣同士が1ビット違いになるように並べる方法だ。 |
グレイ符号ではない、非グレイとは次のような物だ。
| 非グレイ符号のQPSKの信号星座図 |
|---|
 |
|
隣同士が必ずしも1ビットの違いではない。 そのため上図のように2ビットの違いが出る場合もある。 |
グレイ符号を採用する理由。 ビット誤りを減らすためだ。
| 非グレイ符号のQPSKの信号星座図の問題点 |
|---|
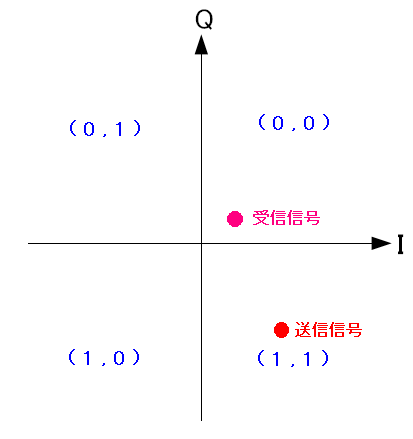 |
|
もし非グレイ符号の信号星座図を使った場合、送信信号が(1,1)でも 雑音などの影響で、受信の際、隣の第一象限の(0,0)に 入ってしまう場合がある。 この場合、2ビットの誤りになってしまう。 |
もし、グレイ符号の場合、受信際に雑音やマルチパスの影響で 隣の領域に入っても、1ビットの誤りで済む。 誤り率を減らすための工夫なのだ。符号化率
OFDM変調の場合、符号化率の値が出てくる。
| OFDM変調 | |
|---|---|
| 1次変調 | 符号化率 |
| BPSK | 1/2 |
| BPSK | 3/4 |
| QPSK | 1/2 |
| QPSK | 3/4 |
| 16QAM | 1/2 |
| 16QAM | 3/4 |
| 64QAM | 2/3 |
| 64QAM | 3/4 |
これって何やねん?? なのだ。 分数になっている値。一体、何なのか調べてみた。 すると、3/4の意味は・・・ 4ビットのうち、3ビットはデータビット という。 わかりにくい表現なのだ。 図式化するとわかりやすいので、図で表してみた。
| 符号化率3/4の意味 |
|---|
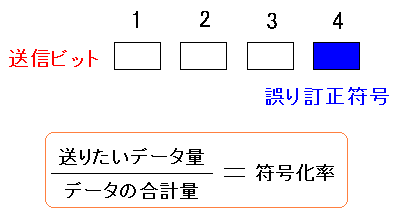 |
|
OFDM変調でデータ送信する場合、誤り訂正符号がつく。 誤り訂正符号が付く事で、送信データ量が増えるため 実質のデータ送信速度が遅くなる。 どれくらい実際に送りたいデータが送れるのかの指標として 符号化率という形であわらしている。 符号化率3/4の場合、送信信号の4ビットのうち 3ビットが実質のデータで、残り1ビットが誤り訂正符号というのだ。 もし、符号化率1/2の場合、半分が誤り訂正符号のため データ送信の際、無駄が出ている事になる。 |
OFDMの場合、1次変調したデジタル信号を、2次加工しないため マルチパスの対策だけでなく、ビット誤りが発生した際の 誤り率の大きさ、誤り訂正符号の話が重要になってくる。 誤り訂正符号については「システム奮闘記:その103」 (メモリの基礎 パソコンのメモリ入門)をご覧ください。
ローパスフィルター(LPF)について
受信波の復調の際、高周波成分を除去するために ローパスフィルターが使われている。
| ローパスフィルター |
|---|
 |
|
コンデンサーは高周波成分を流しやすい性質がある。 その性質を利用して、上図のように高周波を逃す回路が組まれる。 |
だが、それだけの説明だと・・・
ホンマに高周波成分を除去できるんかいな?
と思う。
そこで実際に簡単な模擬実験で確かめる事にした。
ローパス回路を以下のように考える。
| 模擬実験で考えたローパス回路の状態 |
|---|
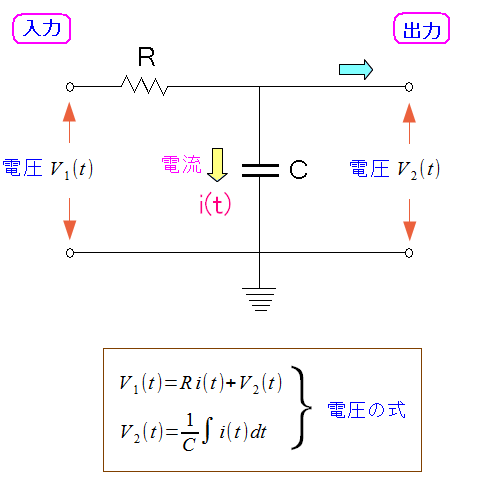 |
|
入力部から高周波を送り、出力部でどういう変化があるのかを見ると 高周波を除去できるのかどうかが、わかる。 まずはコンデンサーを流れる電流を求める事にした。 |
コンデンサーの電流の算出方法だが
| コンデンサーの電流の算出方法(1) |
|---|
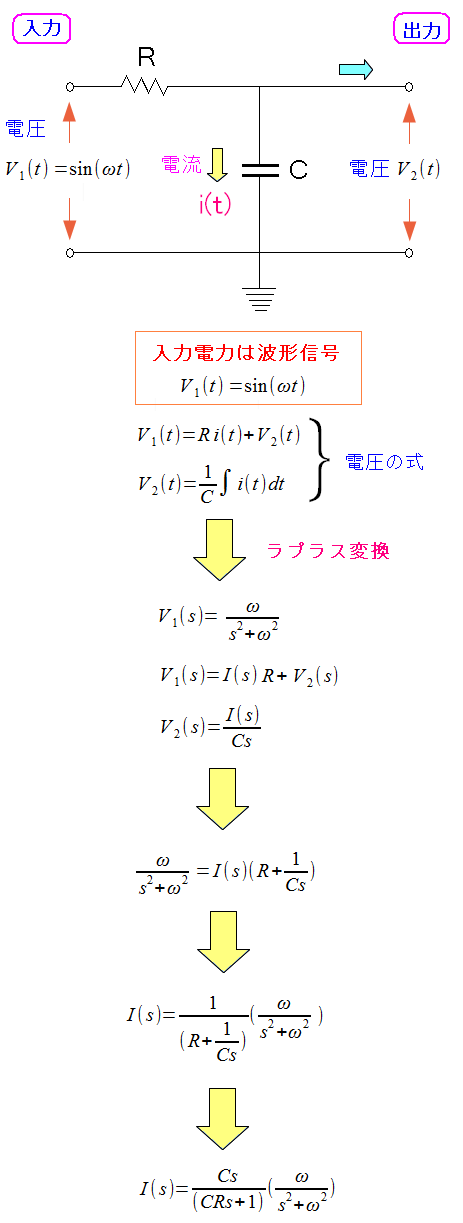 |
|
入力部からは交流の電気を流す事にする。 周波数が高ければ高いほど、コンデンサーに電気が逃げるため 出力部の電圧が低くなる事になる。 だが、微分方程式を解く事はできないため、ラプラス変換を行なう。 ラプラス変換については「システム奮闘記:その98」をご覧ください。 (電気回路入門) ラプラス変換表は以下のサイトをご覧ください。 ラプラス変換表 |
途中で面倒な所にぶつかる。 この形のままでは 逆ラプラス変換が行なえへん! そのため、部分分数分解法を使うのだが・・・ 計算間違いしやすい! という所だ。 注意しながら計算を続ける。
| コンデンサーの電流の算出方法(2) |
|---|
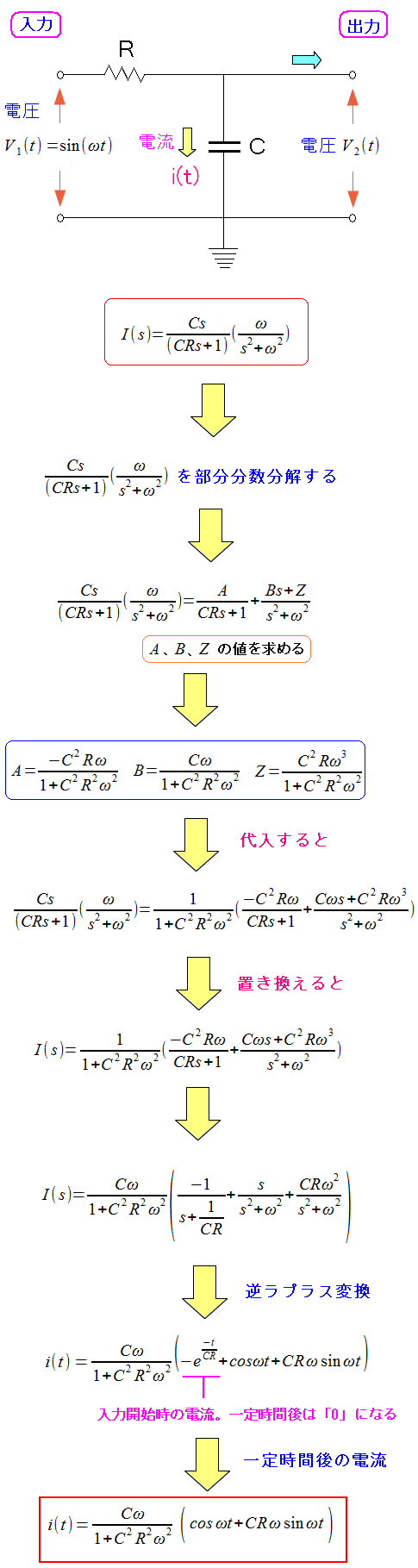 |
|
部分分数分解法を行ない、計算を続ける。 そして逆ラプラス変換を行なって、ようやく電流の式が導けた。 ラプラス変換を使うと、入力開始時の電流まで算出できる。 だが時間が経過すれば、ゼロになるため、その部分は無視する事にする。 定常電流だけを見る事にするのだ。 |
コンデンサーを流れる電流が求まった所で 出力部分の電圧を求める。
| 出力部分の電圧 |
|---|
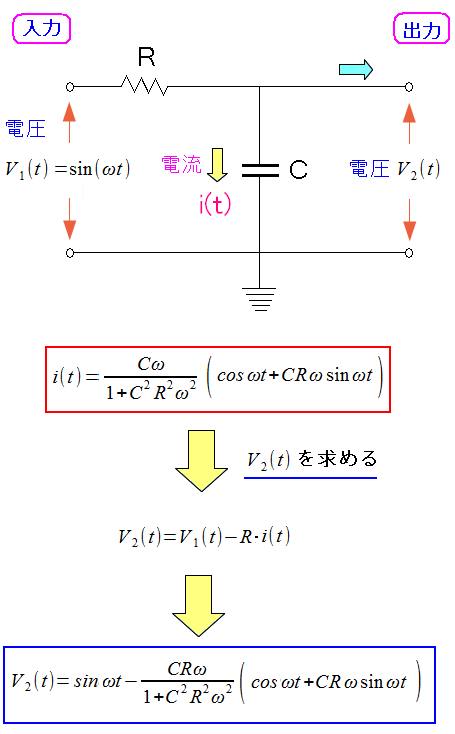 |
|
出力部分の電圧の式が求まった。 |
入力部分の電圧と、出力部分の電圧を比較してみる。
| 入力部分の電圧と、出力部分の電圧(低周波) |
|---|
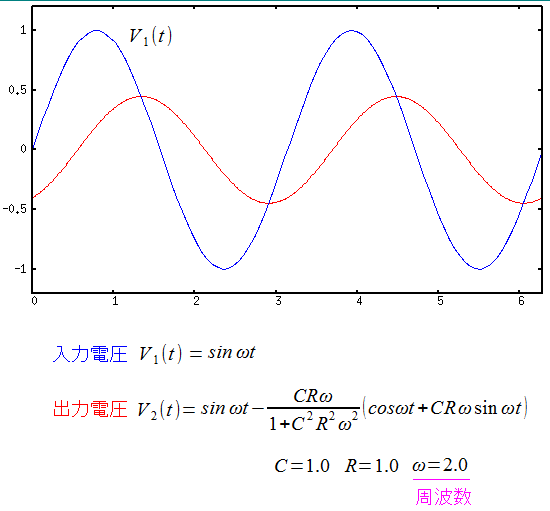 |
|
コンデンサーがあるため、電気が逃げているが それでも出力部でも電圧をとらえている。 あと、コンデンサーの影響で位相が進んでいる。 位相を進ませる事を目的としたコンデンサーの事を 進相コンデンサーという。力率改善などに使われる。 詳しくは「システム奮闘記念:その98」(電気回路入門)をご覧ください。 |
抵抗値、コンデンサーの電気容量の値を固定したまま 入力部分の交流電気の周波数を上げてみる事にした。
| 入力部分の電圧と、出力部分の電圧(高周波) |
|---|
 |
|
出力部の電圧が下がっている。 周波数を上げると、コンデンサー側に逃げる電気が 増加する事がわかった。 |
簡単な模擬実験(数値計算)から ローパスフィルターで高周波成分が除去できる という事が、わかったのだ。
無線LANの実験
いよいよ無線LANの実験を行なう事にした。
| 購入した無線LANアクセスポインタ (IO-DATAのWHG-NAPG/AL) |
|---|
 |
| 無線LANアクセスポインタ WHG-NAPG/AL(IO-DATA) |
私のノートパソコンに無線LANのアダプタがついているのだが・・・ 2.4GHz帯域しか対応してへん!! だった。 5.2GHz帯域での調査はできないものの、2.4GHz帯域は電子レンジや Bluethoothの影響を調べられる。 電波の影響と強度の測定を行なう際、それがわかる便利なソフトが欲しい。 そこで調べてみると 無償のinSSIDerがあった のだ。 無線LANが不安定な原因「チャンネル干渉」を調べるのに役立つフリーソフト「inSSIDer」 - GIGAZINE inSSIDer3.1のダウンロードサイト
| inSSIDerについて |
|---|
|
無線LANアダプタのついたパソコンにインストールするソフトで 無線の強度を測定する事ができる。 Ver3までは無償だが、Ver4からは有償になっている。 そのためver3を使った。 |
次に、色々な部屋をまわってみて、電波強度を調べてみた。
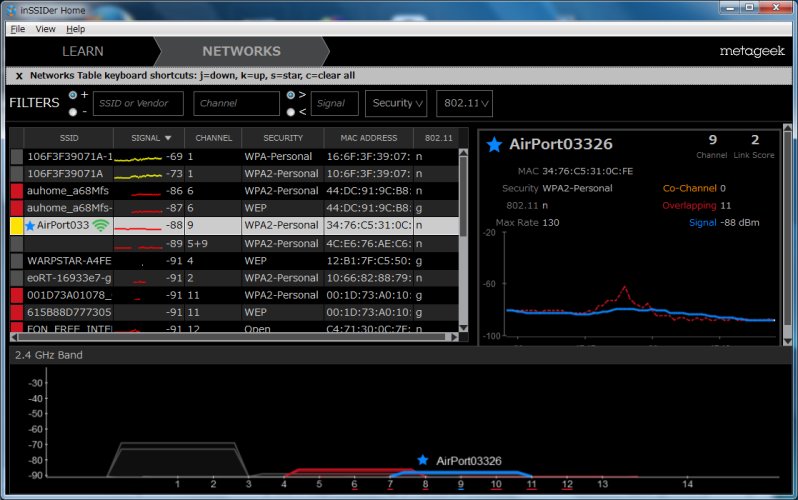
| 事務室の私の机の上(11nの場合) |
|---|
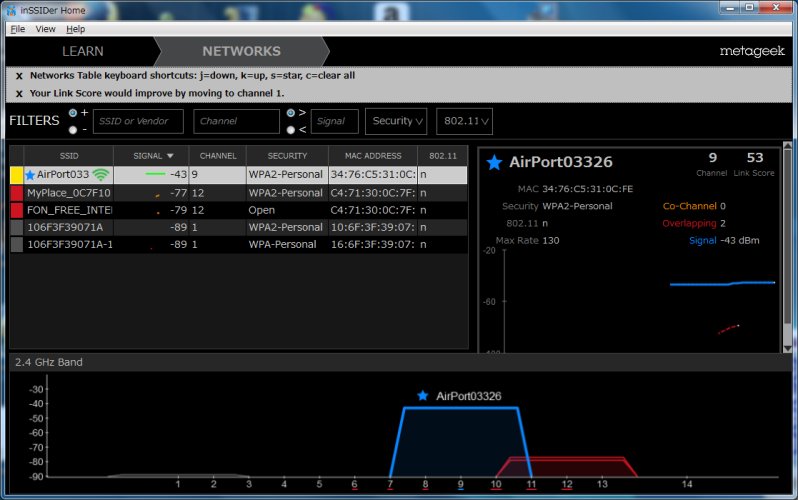 |
|
青く盛り上がっているのが、うちの会社の無線の電波。 11nの場合、台形になっている。 外部の無線LANの電波も拾っているのがわかる。 |
ところで、11bの電波にしてみると、盛り上がりの形状が変わる。
| 事務室の私の机の上(11bの場合) |
|---|
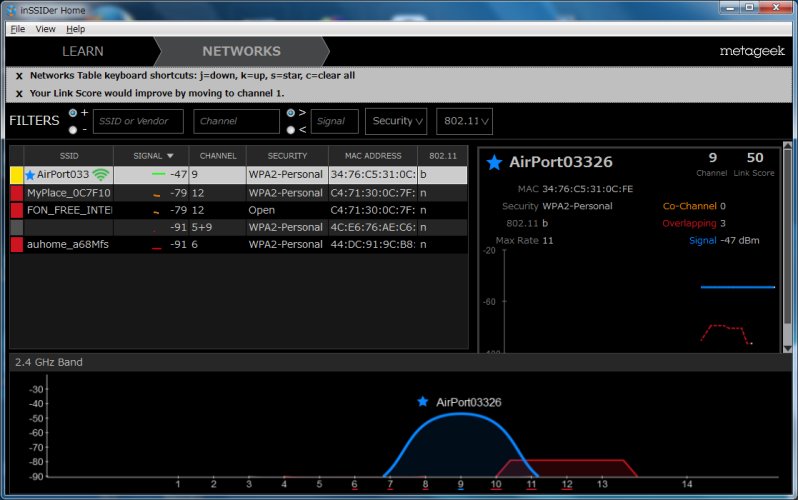 |
|
11bの場合、山型になっている。 もしかして、直接拡散は山のように盛り上がっているから そういう表示にしているのかなぁと思ったりする。 |
社内をウロウロする。
同じ階の別の部屋の電波強度を見ると
外部の電波の方が強いやん!
| 別の部屋での電波強度 (11nの場合) |
|---|
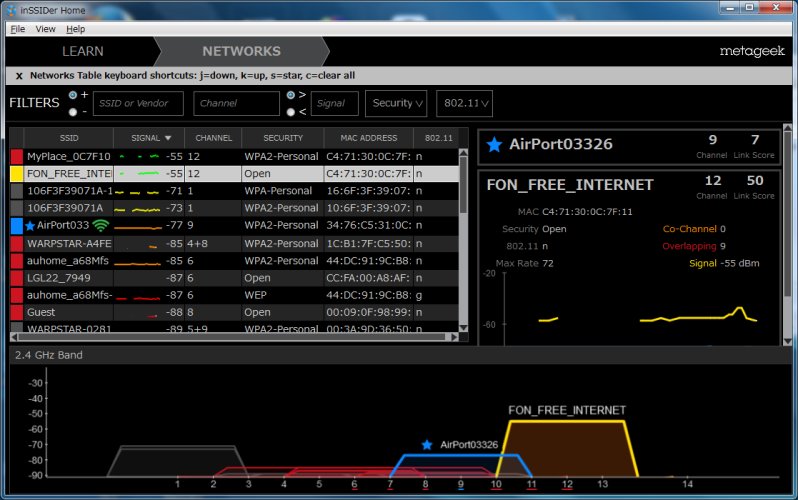 |
|
社内の無線LANの電波よりも、社外の無線LANの電波の方が強い。 一体、何の電波なのか、わからない。 「FON_FREE_INTERNET」という表示だった。 |
一体、どこの無線LANなのか。 近くの大手企業の無線LANなのか? だがこの時は、それ以上、踏み込んで考える事はしなかった。 この部屋では、問題なく無線LANが使えた。
| FON_FREE_INTERNETとは |
|---|
|
FONユーザーが利用できるWiFiだという。 だが、セキュリティー上、問題があるので 「お薦めしない」と書いているサイトがいくつかあった。 使った事がないので、その事については触れる気はない。 fon - WiFi FOR EVERYONE | 世界最大のWiFiコミュニティ fon japanのオフィシャルサイト |
次に3階から1階に移動してみた。
| 1階の部屋での電波強度 (11nの場合) |
|---|
 |
|
電波が弱いのが一目瞭然。 実際、この部屋では通信が途中で切れたりして、通信状態が良くなかった。 |
ところで、電波の強度でデシベルが使われるが デシベルって何やねん? なのだ。 そこで調べてみた。すると以下のサイトを見つけた。 初歩の電波 [無線と電波について] 無線LANでよく見かけるdBなる単位について 電波強度で使われるデシベルの意味は・・・ 信号の電力の比を対数で表したもの だという。 そこで次のような物を考えた。
| 私が思ったデシベルの意味 |
|---|
 |
|
入力信号と受信信号の電力の比を対数で表した物だと思った。 これだと、比が0.001の場合でも、上の式だと-30になるので わかりやすい数字になっているのだ。 (注意) あくまでも私が誤って認識してしまったデシベルの意味です。 私の思い込み・失敗例の紹介のために書いていますので デシベルの意味だと思わないでください!! |
だが、しばらくして次の疑問が出てきた。 どないして入力電力を知るねん? という事で、調べ直す事にした。 すると、以下の2つのサイトを発見。 無線LANの信号強度を表す言葉 RSSIとSNR : 基礎から学ぶ無線LANの設定と設計 Lifelog (屋内編(1) 置き場所やアンテナ角度で感度アップ!:無線LANの新常識) 以下の事が書いていた。 デシベルとは・・・ 受信強度 RSSIの値 であり 1mWの時、0デシベルにした相対値 というのだ。 すなわち、以下の事をいうのだ。
| デシベルとは受信強度(RSSI)の値 |
|---|
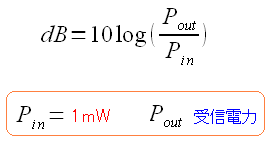 |
|
1mWを基準にし、受信信号の電力強度との比率だ。 |
そして受信強度の目安表も載っていた。
| RSSIの値 | |
|---|---|
| -39dB以上 | かなり強い |
| -49dB〜-40dB | 強い |
| -59dB〜-50dB | 普通 |
| -79dB〜-60dB | 弱い |
| -80dB以下 | 接続しにくい |
どうやら目安として・・・ -80dB以上の値は必須 のようだ。 それにしても、1mWを基準にしている事を発見していなければ 間違えた事を書いて、大恥をかく所だった。2.4GHz帯域における電子レンジの影響について
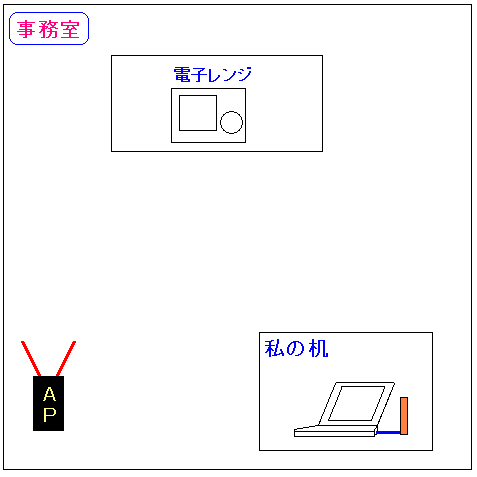
2.4GHz帯域は、電子レンジやbuletoothの影響を受ける。 そこで、電子レンジを使って、無線LANの影響を調べてみる事にした。 まず実験環境は以下のようにした。
| 無線LANでの電子レンジの影響の実験環境 |
|---|
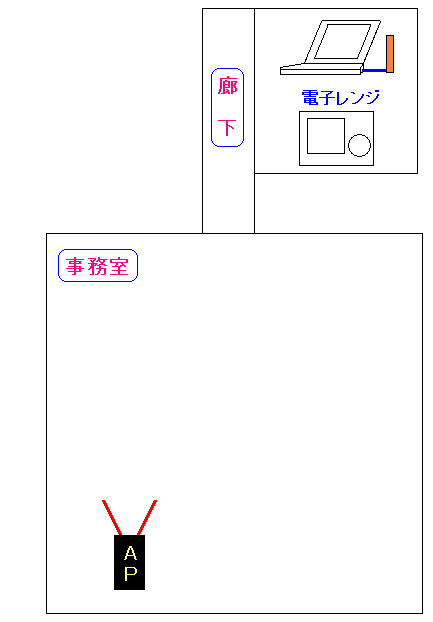 |
|
無線LANアクセスポイントは事務室に置いて ノートパソコンは電子レンジのある台所で 電子レンジが稼働していない時と、稼働中の時の 無線LANでの通信速度を算出する事にしてみた。 |
電子レンジがある台所の電波状況を見てみる。
| 電子レンジがある台所の電波状況 |
|---|
 |
| inSSIDerで電波状況を見てみる。全然、問題ない。 |
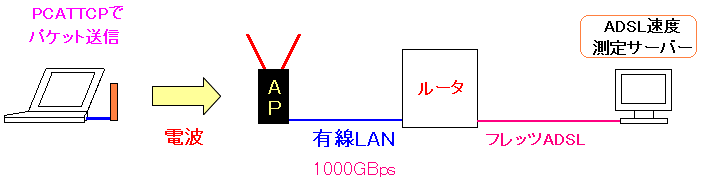
ところで、無線LANの速度測定の実験方法だが・・・
速度測定のソフトがあらへん!!
だった。
そこで知恵をしぼって、以下の方法を考えた。
| 無線LANの通信速度の測定方法 |
|---|
 |
|
ADSLの速度測定を使ってみる事にした。 もし、電子レンジの影響で無線部分の通信速度が激減したら ADSLの通信速度まで影響できると考えたからだ。 |
| 速度測定の様子 |
|---|
 |
| 電子レンジの前に立って実験中。 |
結果が出た。
| 実験結果(11nで実験) |
|---|
 |
|
電子レンジの有無関係なく、結果は、だいたい700Kpbsで ほぼ同じ結果だった。 |
ここで電波の影響は受けないと結論づけようと思ったが ある事に気づいた。 妨害電波による無線LANの通信速度の遅さよりも ADSLの回線の方が遅ければ、この方法は使えへん! つまり、ADSL回線の速度測定の方法は、全く使えない事がわかった。
| あとでわかった話 |
|---|
|
11nを使うと、今回行なった実験環境では 電子レンジを使った場合でも1MBps以上の通信速度が得られる。 ADSLは、それよりも遅いため、意味のない実験になってしまった。 |
そこで無線LANの速度を、できるだけ正確に測定するソフトがないか
探してみたら、見つかった。
無線区間のスループットを測ろう!
PCATTCPというソフトなのらー!!
善は急げで測定する事にした。
測定方法は以下の通りだ。
| ソフトを使った無線LANの通信速度の測定方法 |
|---|
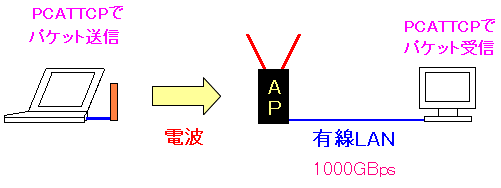 |
|
パケットが往復するまでの時間を測定する事で 無線LANの通信速度を測ろうというのだ。 もちろん有線LANは1GBpsを使っているので無線LANより速く それが測定に影響する事はないと考えられる。 |
まずは11bから測定してみた。
| 11bで測定実験 |
|---|
| 電子レンジなし |
C:\lan>PCATTCP -t -f m -n 256 192.168.X.Y
PCAUSA Test TCP Utility V2.01.01.14 (IPv4/IPv6)
IP Version : IPv4
Started TCP Transmit Test 0...
TCP Transmit Test
Transmit : TCPv4 0.0.0.0 -> 192.168.X.Y:5001
Buffer Size : 8192; Alignment: 16384/0
TCP_NODELAY : DISABLED (0)
Connect : Connected to 192.168.X.Y:5001
Send Mode : Send Pattern; Number of Buffers: 256
Statistics : TCPv4 0.0.0.0 -> 192.168.X.Y:5001
2097152 bytes in 4.598 real seconds = 3.48 Mbit/sec +++
numCalls: 256; msec/call: 18.391; calls/sec: 55.678
C:\lan>
|
| 電子レンジあり |
C:\lan>PCATTCP -t -f m -n 8 192.168.X.Y
PCAUSA Test TCP Utility V2.01.01.14 (IPv4/IPv6)
IP Version : IPv4
Started TCP Transmit Test 0...
TCP Transmit Test
Transmit : TCPv4 0.0.0.0 -> 192.168.X.Y:5001
Buffer Size : 8192; Alignment: 16384/0
TCP_NODELAY : DISABLED (0)
Connect : Connected to 192.168.X.Y:5001
Send Mode : Send Pattern; Number of Buffers: 8
Statistics : TCPv4 0.0.0.0 -> 192.168.X.Y:5001
65536 bytes in 4.516 real seconds = 0.11 Mbit/sec +++
numCalls: 8; msec/call: 578.081; calls/sec: 1.771
C:\lan>
|
もろ電子レンジの影響を受けとる!
だった。
次に11gで測定してみた。
| 11gで測定実験 |
|---|
| 電子レンジなし |
C:\lan>PCATTCP -t -f m -n 128 192.168.X.Y
PCAUSA Test TCP Utility V2.01.01.14 (IPv4/IPv6)
IP Version : IPv4
Started TCP Transmit Test 0...
TCP Transmit Test
Transmit : TCPv4 0.0.0.0 -> 192.168.X.Y:5001
Buffer Size : 8192; Alignment: 16384/0
TCP_NODELAY : DISABLED (0)
Connect : Connected to 192.168.X.Y:5001
Send Mode : Send Pattern; Number of Buffers: 128
Statistics : TCPv4 0.0.0.0 -> 192.168.X.Y:5001
1048576 bytes in 0.476 real seconds = 16.82 Mbit/sec +++
numCalls: 128; msec/call: 3.805; calls/sec: 269.119
|
| 電子レンジあり |
C:\lan>PCATTCP -t -f m -n 8 192.168.X.Y
PCAUSA Test TCP Utility V2.01.01.14 (IPv4/IPv6)
IP Version : IPv4
Started TCP Transmit Test 0...
TCP Transmit Test
Transmit : TCPv4 0.0.0.0 -> 192.168.X.Y:5001
Buffer Size : 8192; Alignment: 16384/0
TCP_NODELAY : DISABLED (0)
Connect : Connected to 192.168.X.Y:5001
Send Mode : Send Pattern; Number of Buffers: 8
Statistics : TCPv4 0.0.0.0 -> 192.168.X.Y:5001
65536 bytes in 0.061 real seconds = 8.25 Mbit/sec +++
numCalls: 8; msec/call: 7.757; calls/sec: 132.006
C:\lan>
|
電子レンジを使っている場合でも、8.25MBpsの速度があるため
ADSL回線の速度が8Mタイプを使っている事もあり
インターネットを使う分には・・・
11gだと影響はあるが運用には耐えられる
だった。
| 実験結果について |
|---|
|
本やネットでは11bは電子レンジの影響を受けると書いていた。 だが、11bは直接拡散方式(DSSS)なので、妨害電波は拡散されて 上手に信号を取り出せるのではないかと疑問に思っていた。 だが、実際には、電子レンジの影響を大きく受けたのがわかった。 OFDM方式の11gの場合、電子レンジの影響は受けたものの それでも問題なく通信ができた。 |
次に、事務所のカウンターに電子レンジを置いた状態で実験をした。
| 電子レンジの実験(2) |
|---|
 |
|
この状態で、どれくらい電子レンジの影響を受けるのか 調べてみる事にした。 |
2,4GHz帯域を使う11b、11g、11nを使う。 そして実験をする。
| 11bでの実験結果 |
|---|
| 電子レンジなし |
C:\lan>PCATTCP -t -f m -n 8 192.168.X.Y
PCAUSA Test TCP Utility V2.01.01.14 (IPv4/IPv6)
IP Version : IPv4
Started TCP Transmit Test 0...
TCP Transmit Test
Transmit : TCPv4 0.0.0.0 -> 192.168.X.Y:5001
Buffer Size : 8192; Alignment: 16384/0
TCP_NODELAY : DISABLED (0)
Connect : Connected to 192.168.X.Y:5001
Send Mode : Send Pattern; Number of Buffers: 8
Statistics : TCPv4 0.0.0.0 -> 192.168.X.Y:5001
65536 bytes in 0.114 real seconds = 4.39 Mbit/sec +++
numCalls: 8; msec/call: 14.593; calls/sec: 70.171
C:\lan>
|
| 電子レンジ有 |
C:\lan>PCATTCP -t -f m -n 8 192.168.X.Y
PCAUSA Test TCP Utility V2.01.01.14 (IPv4/IPv6)
IP Version : IPv4
Started TCP Transmit Test 0...
TCP Transmit Test
Transmit : TCPv4 0.0.0.0 -> 192.168.X.Y:5001
Buffer Size : 8192; Alignment: 16384/0
TCP_NODELAY : DISABLED (0)
Connect : Connected to 192.168.X.Y:5001
Send Mode : Send Pattern; Number of Buffers: 8
Statistics : TCPv4 0.0.0.0 -> 192.168.X.Y:5001
65536 bytes in 2.098 real seconds = 0.24 Mbit/sec +++
numCalls: 8; msec/call: 268.508; calls/sec: 3.814
C:\lan>
|
11bだと全く使い物にならへん!!
だった。
次に11gで実験してみる。
| 11gでの実験結果 |
|---|
| 電子レンジなし |
C:\lan>PCATTCP -t -f m -n 64 192.168.X.Y
PCAUSA Test TCP Utility V2.01.01.14 (IPv4/IPv6)
IP Version : IPv4
Started TCP Transmit Test 0...
TCP Transmit Test
Transmit : TCPv4 0.0.0.0 -> 192.168.X.Y:5001
Buffer Size : 8192; Alignment: 16384/0
TCP_NODELAY : DISABLED (0)
Connect : Connected to 192.168.X.Y:5001
Send Mode : Send Pattern; Number of Buffers: 64
Statistics : TCPv4 0.0.0.0 -> 192.168.X.Y:5001
524288 bytes in 0.225 real seconds = 17.81 Mbit/sec +++
numCalls: 64; msec/call: 3.594; calls/sec: 284.937
|
| 電子レンジ有 |
C:\lan>PCATTCP -t -f m -n 64 192.168.X.Y
PCAUSA Test TCP Utility V2.01.01.14 (IPv4/IPv6)
IP Version : IPv4
Started TCP Transmit Test 0...
TCP Transmit Test
Transmit : TCPv4 0.0.0.0 -> 192.168.X.Y:5001
Buffer Size : 8192; Alignment: 16384/0
TCP_NODELAY : DISABLED (0)
Connect : Connected to 192.168.X.Y:5001
Send Mode : Send Pattern; Number of Buffers: 64
Statistics : TCPv4 0.0.0.0 -> 192.168.X.Y:5001
524288 bytes in 2.065 real seconds = 1.94 Mbit/sec +++
numCalls: 64; msec/call: 33.035; calls/sec: 30.997
C:\lan>
|
11gも結構辛い・・・
のだ。
次に11nで試してみた。
| 11nでの実験結果 |
|---|
| 電子レンジなし |
C:\lan>PCATTCP -t -f m -n 64 192.168.X.Y
PCAUSA Test TCP Utility V2.01.01.14 (IPv4/IPv6)
IP Version : IPv4
Started TCP Transmit Test 0...
TCP Transmit Test
Transmit : TCPv4 0.0.0.0 -> 192.168.X.Y:5001
Buffer Size : 8192; Alignment: 16384/0
TCP_NODELAY : DISABLED (0)
Connect : Connected to 192.168.X.Y:5001
Send Mode : Send Pattern; Number of Buffers: 64
Statistics : TCPv4 0.0.0.0 -> 192.168.X.Y:5001
524288 bytes in 0.152 real seconds = 26.31 Mbit/sec +++
numCalls: 64; msec/call: 2.432; calls/sec: 421.026
|
| 電子レンジ有 |
C:\lan>PCATTCP -t -f m -n 8 192.168.X.Y
PCAUSA Test TCP Utility V2.01.01.14 (IPv4/IPv6)
IP Version : IPv4
Started TCP Transmit Test 0...
TCP Transmit Test
Transmit : TCPv4 0.0.0.0 -> 192.168.X.Y:5001
Buffer Size : 8192; Alignment: 16384/0
TCP_NODELAY : DISABLED (0)
Connect : Connected to 192.168.X.Y:5001
Send Mode : Send Pattern; Number of Buffers: 8
Statistics : TCPv4 0.0.0.0 -> 192.168.X.Y:5001
65536 bytes in 0.033 real seconds = 15.15 Mbit/sec +++
numCalls: 8; msec/call: 4.224; calls/sec: 242.412
C:\lan>
|
11nだと、電子レンジあっても使える範囲だと思う。 ただし、動画やデータのダウンロードする場合は辛いと思うが、 メールや重たくないサイトを見る限りは、問題なく使えると思う。
設定をしながら覚える無線LANの仕様や規格
無線LANの装置を触ろうとすると、色々な設定画面が出てくる。
| IO-DATAのWHG-NAPG/ALの「基本な設定」の画面 |
|---|
 |
| 11nの場合、20MHz帯域か40MHz帯域かの選択ができる。 |
実際に設定が反映されているのかどうか、確かめてみる事にした。
| 帯域幅の違いがinSSIDerで見れる |
|---|
| 20MHz帯域の場合 |
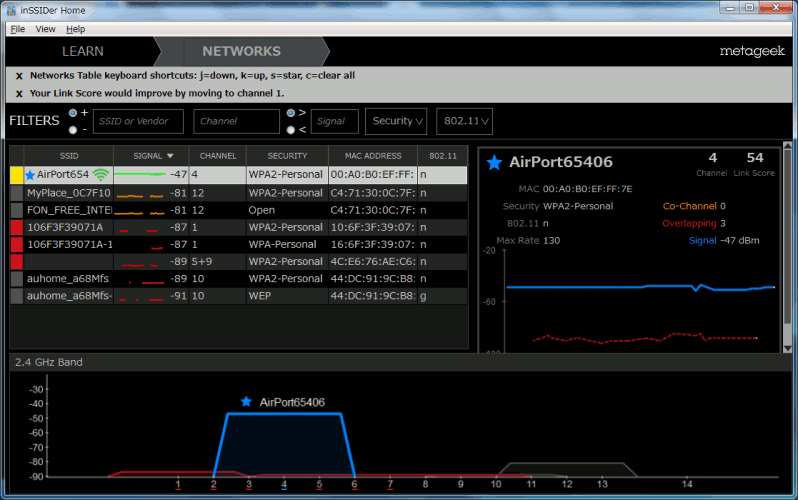 |
| 40MHz帯域の場合 |
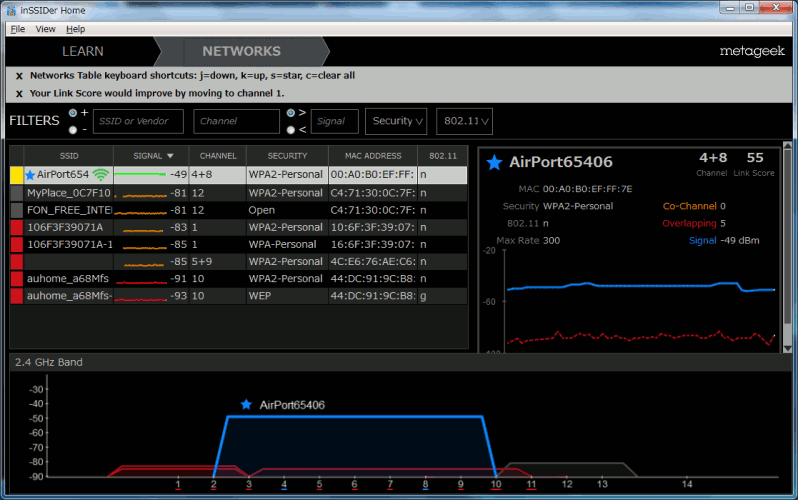 |
| 電波強度を見るソフト「inSSIDer」で帯域幅の違いまでわかる。 |
基本設定は、これぐらいとして、高度な設定を見てみた。
| IO-DATAのWHG-NAPG/ALの「高度な設定」の画面 |
|---|
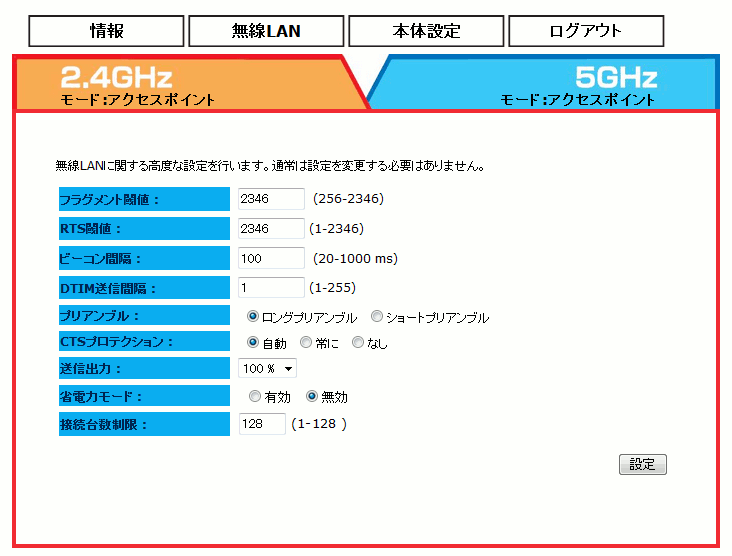 |
| 「高度な設定」で用意されている設定項目だ。 |
うちの会社のような使い方だと、高度な設定は無視して 初期値のまま使っても良いのだが、知っておいても損はしないので 設定項目を見ていく事にした。
| ビーコン間隔 |
|---|
 |
| 初期設定では、ビーコン間隔は「100ms」になっている。 |
初期値では100msごとにビーコンの信号を送るというが・・・ ビーコンって何やねん? 最初からつまづいた。そこで調べてみる事にした。 無線通信で同期を取るための信号 なのだ。 図で描くと以下のようになる。
| ビーコンとは |
|---|
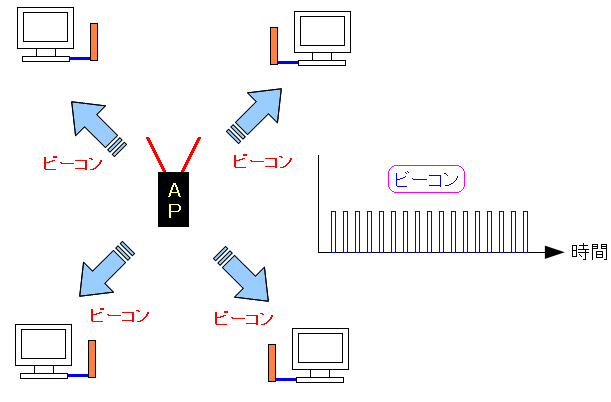 |
|
アクセスポインタの傘下にあるパソコンなどに対して 同期をとるために送る信号の事だ。 |
ピアノでいう
メトロローム
なのだ。
ビーコンがわかった所で、次を見てみる。
DTIM送信間隔だ。
| DTIM送信間隔の設定 |
|---|
 |
| DTIM送信間隔で、初期値は「1」になっている。 |
ここでも、やっぱり・・・ DTIM送信間隔って何やねん? なのだ。 そこで調べてみた。 【上級】無線LANの正しい構築法 第10回(日経ITPro) 無線ブロードバンドルーター オンラインマニュアル for WN-G54/R(IODATA) DTIMとは Delivery Traffic indication messageの略 だという。 日本語にすると 送信待ちを伝える伝言 なのだ。 いまいちわからないので図にしてみた。
| ビーコンとDTIMとの関係 |
|---|
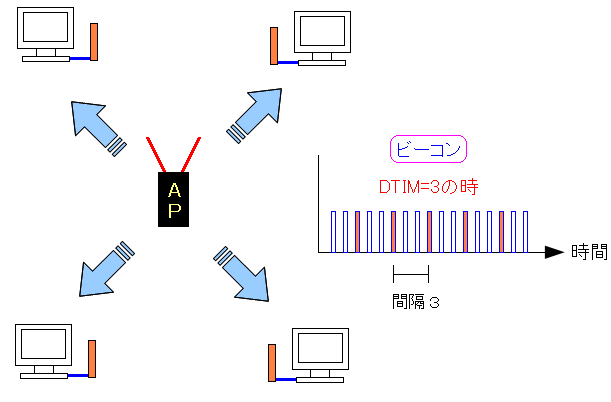 |
|
DTIMの値とは、ビーコンの何個目にDTIM信号を入れるかの値になる。 上図のように、DTIM=3の場合、ビーコンが3個ごとにDTIM信号を入れているのだ。 |
DTIMの目的を調べてみると
電力節約
だという。
| 無線端末の電力節約が目的 |
|---|
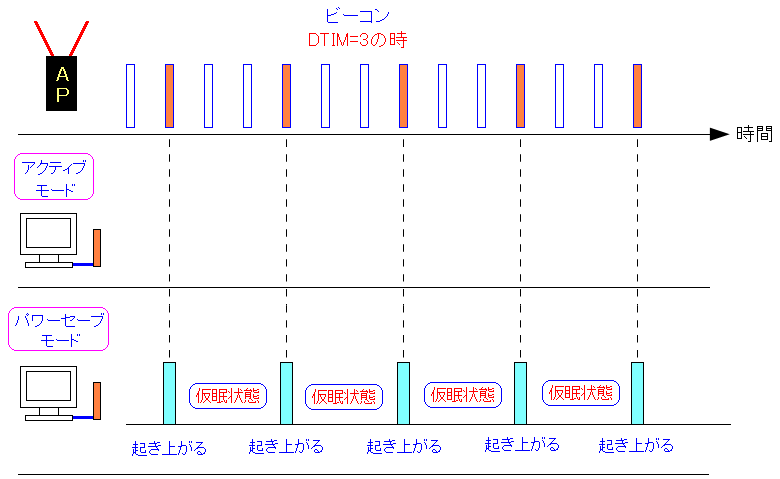 |
|
アクティブモードの端末は常に稼働しているため電力を消費する。 セーフパワーモードの端末の場合、受信のみ行ない、電力消費を抑え DTIM信号が来た時のみ全てを稼働させる仕組みだ。 |
DTIM信号によって、時々、端末を起こして動かすため
電力消費を抑えるという。
だが、調べてみるとDTIMは曲者らしい。
眠れない端末? "くせ者"パワーセーブモード(ITmediaエンタープライズ)
だが、深く踏み込み気は起こらない。
調べるとドツボにハマる
のが目に見えている。
そこで逃げる事にして、次の項目を見てみる事にした。
| ロングプリアンブルとショートプリアンブル |
|---|
 |
|
この機種の初期値は「ロングプリアンブル」になっている。 メーカや機種によっては「ショート」が初期値になっている場合もある。 |
ロングプリアンブルとショートプリアンブルとの違い。 調べてみると、こんな理由が見つかった。
| ロングプリアンブルとショートプリアンブルとの違い | |
|---|---|
| (1) | 古い無線端末はロングしか対応していない |
| (2) | ショートだと通信が高速通信ができる |
古い無線LANアダプタを付けているパソコンにも対応するため ロングプリアンブルにした方が無難のようだ。 ところで・・・ プリアンブルって何やねん? なのだ。 プリアンブルが何かがわからずに話を書いても仕方がない。 そこで調べてみる事にした。 英語の綴りで「preamble」という単語だ。 その意味を調べてみると 序文、前置き という意味だ。 では通信ではどういう意味なのか、調べてみる事にした。 IT用語辞典では以下のように書いていた。
| プリアンブルの意味(通信の意味では) |
|---|
|
デジタル通信の分野で、受信側に「これからデータが送られている」事を 知らせるために、事前に送る、決まったビット列の事。 プリアンブルとは(IT用語辞典) |
なんとなく、わかったような、わからんような内容だが
もう少し調べてみると・・・
無線LAN(IEEE802.11)のフレームフォーマット - ネットワークエンジニアを目指して
同期を取るための信号
なのだ。
ところで一体、プリアンブルとはどういう物なのか
通信パケットの形を見てみる事にした。
| パケットの中のプリアンブル(Preamble) |
|---|
 |
|
物理層でパケットに付加される物だ。 その後ろにはデータリンク層で付加されるMACフレームがある。 |
ところで・・・ PCLPとは何やねん? なのだ。 わかった気になって、PCLPと書いても、それが何かわからずに 書いていたのでは、ネットや本の丸写ししているのが、バレる。 そこで調べてみると Physical Layer Convergence Protocol/Procedure なのだ。 直訳すると・・・ 物理層集中通信規約 全く意味が理解できへん・・・。 そこで、忍法「先送りの術」で、わからないまま、放置する事にした。 ところで、ロングプリアンブルとショートプリアンブルとの違いだが 11bの規格で、その違いがわかりやすく図式化されているサイトを見つけた。 無線LAN - IEEE802.11フレームフォーマット
| ロングプリアンブルとショートプリアンブルとの違い(IEEE802.11b) |
|---|
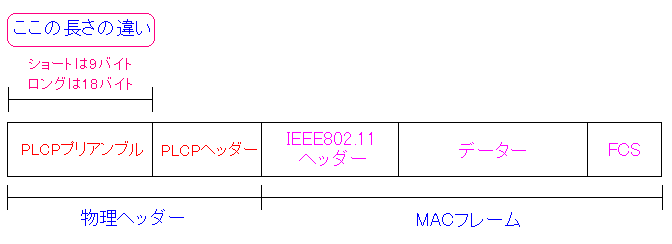 |
|
ロングプリアンブルは18バイトの信号だ。 ショートプリアンブルは9バイトの信号で文字通り、短くなっている。 |
ところでロングプリアンブルとショートプリアンブルの違いで 物理層の伝送速度の違いがあるようだ。
| ロングプリアンブルとショートプリアンブルとの違い | |
|---|---|
| ロング | プリアンブルとヘッダーは、1Mbpsで送信される |
| ショート | プリアンブルとヘッダーは、2Mbpsで送信される |
だがインテルのサイトでは、違った事を書いている。 インテル® Wi-Fi 製品 — プリアンブルとは?
| ロングプリアンブルとショートプリアンブルとの違い (インテルのサイト) | |
|---|---|
| ロング | 物理層の部分は、1Mbpsで送信される |
| ショート |
プリアンブル部分は1Mbpsで送信され ヘッダー部分は2Mbpsで送信される |
どっちが正しいねん!
と思った。
だが、調べる気力がないので「忍法先送りの術」で逃げる事にした。
これを放置という。
ところで物理層で付加される部分を、少し踏み込んで見ている。
| 物理層で付加される部分 |
|---|
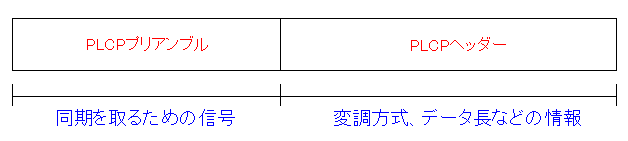 |
|
物理層で付加される部分は、プリアンブル(Preamble)とヘッダーだ。 プリアンブルは同期をとる役目で、ヘッダーには変調方式や データ長などの情報が入っている。 |
ヘッダー部分がどういう構造になっているのか調べてみると
無線LANの規格によって構造が異なる
だった。
調べてみても、わかりやすい資料がなかったので諦める事にした。
プリアンブルの部分を詳しく見てみる。
| プリアンブル部分を詳しく見ると |
|---|
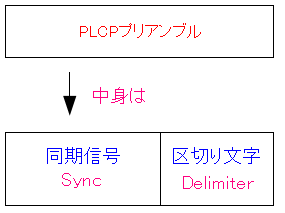 |
|
同期(Sync)部分とデリミタ(delimiter)部分だ。 デリミタを辞書で調べると「区切り文字」だった。 |
一体、どうなっているのか調べてみる事にしたが
本やネットで調べたが情報が見つからへん
だった。
だが、有線LANのイーサーネット(Ethernet:IEEE802.3)でも
同じように物理層で付加される物としてプリアンブルがある。
詳説 TCP/IPプロトコル:第7回 イーサネット(その2) - イーサネットのフレーム構造 (3/3) - @IT
似たような構造の可能性が高いので、参考までに見てみる事にした。
| イーサーネットでのプリアンブル |
|---|
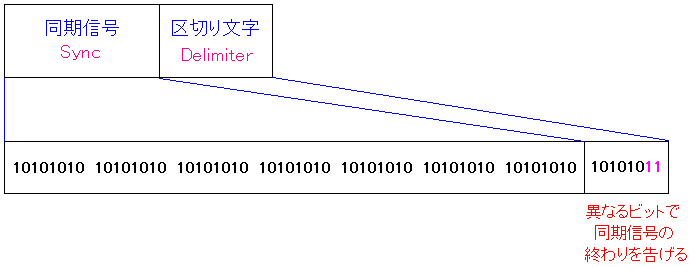 |
|
同期部分は「10」の繰り返しで、デリミタ部分の最後が「11」だ。 最後の部分で異なるビットを入れる事で、終了を伝えている。 つまり区切りに当たるので「区切り文字」のデリミタになっているのだ。 |
これ以上、調べてもドツボにハマるだけなので諦めた。 次の項目を見てみる事にした。
| CTSプロテクション |
|---|
 |
| 初期値では「自動」になっている。 |
ところで・・・
CTSプロテクションって何やねん?
なのだ。
CTSとは隠れ端末問題の話で出てきたパケットだ。
調べてみると、衝突防止のRTS/CTS制御を行なうかどうかの設定だ。
この場合、自動になっているので、アクセスポインタが自動で選択するようだ。
衝突防止機能を使えば、パケットの衝突は防げるのだが
パケットのやりとりが増えるため、通信速度は遅くなる。
ぶらさがっている端末が少ない場合、この機能を使わない事を
推奨している場合がある。
次はRTS閾値の設定だ。
| RTS閾値の設定 |
|---|
 |
|
RTS/CTSフロー制御を行なう際、フレームの大きさが どれくらい以上から行なうのかを基準の値だ。 RTS閾値が小さい場合、ちょっとしたフレームでも衝突防止を行なうため パケットのやりとりが増え、結果、通信速度が遅くなる。 |
次の項目は送信電力の設定だ。
| 送信電力の設定 |
|---|
 |
|
電波送信の出力の選択で、初期値は最大の100%になっている。 この値を触る事で、電波の飛ぶ距離を調整して 近くに設置している、他の無線LANとの競合を防ぐのが目的だ。 |
送信電力と距離との関係だが・・・
わからへん!
なのだ。
ここまでくると、電波工学になってくる。
ちょっと調べてみた。
第5回 無線LANと通信距離について(1)
無線 LAN と通信距離について(1)|Wireless・のおと|サイレックス・テクノロジー株式会社
するとフリスの伝達公式が載っていた。
| フリスの伝達公式 |
|---|
 |
|
これを見ると、電波の強さは距離の2乗に反比例し 波長に2乗に比例している。 受信利得、送信利得が定数と考えると 距離が倍になると受信電力は4分の1になる |
ここから先、踏み込んでいくには電磁気学や電波工学の知識が 必要になってくるのだが、変調の話で、だいぶ労力を使い果たしたため とても調べる気が起こらないので、将来、電波を取り上げる機会があれば 取り上げたいと思います。 ところで11nを使っていると、11nデータレートの設定画面が出てくる。
| 11nのデータレートの設定 |
|---|
 |
| 初期値は自動になっている。 |
設定には、どんな選択肢があるのか見てみる事にした。
| 11nのデータレートの選択肢 |
|---|
 |
| データレートは、MCS値の設定を行なう。 |
ところで・・・
MCS値って何やねん?
なのだ。
そこで調べてみると、11nで通信を行なう際の
変調方法や符号化率の違いを表す物だという。
高速無線LAN情報局
MCSの一覧表は、以下のサイトに出ていた。
802.11n の設計および導入に関するガイドライン - Cisco Systems
早速、丸写しをする事にした。
| 11nのデータレート表 | |||||||
|---|---|---|---|---|---|---|---|
| MCS | ストリーム 並行送信数 |
変調方式 | 符号化率 | ガードインターバル (800ns) |
ガードインターバル (400ns) | ||
| 20MHz | 40MHz | 20MHz | 40MHz | ||||
| 0 | 1 | BPSK | 1/2 | 6.5 | 13.5 | 7 2/9 | 15.0 |
| 1 | QPSK | 1/2 | 13.0 | 27.0 | 14 4/9 | 30.0 | |
| 2 | QPSK | 3/4 | 19.5 | 40.5 | 21 2/3 | 45.0 | |
| 3 | 16QAM | 1/2 | 26.0 | 54.0 | 28 8/9 | 60.0 | |
| 4 | 16QAM | 1/2 | 39.0 | 81.0 | 43 1/3 | 90.0 | |
| 5 | 64QAM | 1/2 | 52.0 | 108.0 | 57 7/9 | 135.0 | |
| 6 | 64QAM | 2/3 | 58.5 | 121.5 | 65.0 | 135.0 | |
| 7 | 64QAM | 3/4 | 65.0 | 135.0 | 72 2/9 | 157.5 | |
| 8 | 2 | BPSK | 1/2 | 13.0 | 27.0 | 14 4/9 | 30.0 |
| 9 | QPSK | 1/2 | 26.0 | 54.0 | 28 8/9 | 60.0 | |
| 10 | QPSK | 3/4 | 39.0 | 81.0 | 43 1/3 | 90.0 | |
| 11 | 16QAM | 1/2 | 52.0 | 108.0 | 57 7/9 | 120.0 | |
| 12 | 16QAM | 1/2 | 78.0 | 162.0 | 86 2/3 | 180.0 | |
| 13 | 64QAM | 1/2 | 104.0 | 216.0 | 115 5/9 | 240.0 | |
| 14 | 64QAM | 2/3 | 117.0 | 243.0 | 130.0 | 270.0 | |
| 15 | 64QAM | 3/4 | 130.0 | 270.0 | 144 4/9 | 300.0 | |
会社で購入した無線LANはアンテナが2本しかないので MCSが15番までしか設定できないが、アンテナ4本の場合は MCSが31番まである のだ。 ただ、MCSの番号だけではガードインターバル(GI)の設定と 帯域設定(20MHzか40MHz)はできないので、個々の設定になってくる。
営業所に無線LANの設置
だいたい無線LANのアクセスポイントの設定の仕方がわかってきた。 ここで変な知識を持ってしまった。 11bと11gの衝突問題 だった。 そこで思った。古い規格は切り捨てよう。なので 11nだけにしてしまえ! というわけで、営業所に送った無線アクセスポインタは 11nのみの通信で設定してしまった。 営業所に送った。営業所長がノートパソコンを持っていたので 接続実験をしてくれる事になった。 だが、接続できない。 悩んだ挙句、ふと無線LANの規格が過った。 もしかして、11n以外かもしれへん そしてアクセスポイントに接続して、11a/11b/11gでも接続可能にして もう一度、所長に試してもらう事にした。 すると接続できた。
| 11gのパソコンを使っていた |
|---|
 |
|
アクセスポイントに接続してみると 端末が使用している無線LANの規格がわかる。 この時、11gを使っているのがわかったのだ。 |
所長が苦笑いしながら 俺のパソコン古くて悪かったなぁ と言われてしまった。 でも、こんな経験を積む事で、1つ1つ運用面での問題点を 洗い出せると開きなおる私だったのだ。
最後に 無線LANの導入。 営業所で来客向けで数人が使う前提で導入する事になりました。 有線と違い、無線は目に見えない上、色々な規格があるので この際だから、徹底的に調べてみようと思い、調べだしたら 物理層やの数学中心の話になってしまいました。 お蔭で、編集で疲れ果てたため、データリンク層や 運用で肝心のセキュリティーなどの話が載せられませんでした。 でも、数学関係で思い出した事、新しく知った事があり 今後、何かに生かせそうです。