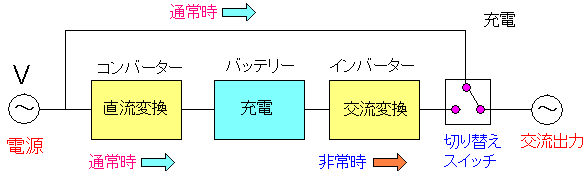
機器に送っている。と同時に充電を行なっている
非常時になると、スイッチが入れ替わり、バッテリーから
電力を供給する仕組みになっている。
安くい分、スイッチが切り替わる際、ほんの僅かの時間でも
サーバーが落ちてしまう可能性は捨てきれない所が
問題点なのだ。
システム奮闘記:その98
はじめに この章では電気回路の説明のために三角関数や 微分積分を使っています。 私には数式を使わずに説明できるような離れ技ができませんので 数式を使いました。 2016年、改定にあたり 2015年から1年間かけて電磁気学を勉強しなおした結果 間違いや怪しい記述があるのを発見してしまい、改定しました。 でも、私の間違いを隠蔽する気はないので、間違いと 間違い修正を併記する事にしました。 包み隠さない編集方針を貫くためです!!
UPS買い替えの経緯
2011年11月の平日。 代休をとって自宅で、のんびりシステム奮闘記の原稿を書いていた私。 だが、そんな幸せを吹っ飛ばす電話が会社からかかってきた。 瞬電が起こってサーバーが落ちた! 雷が発生して瞬電が起こったというのだ。 無停電装置(UPS)があるのだが、UPSが作動しなかったのだ。 だが、幸いな事にサーバーは全て仮想化している。 自宅からVPNで会社に接続して、仮想化ソフトを遠隔操作して サーバーを復旧させた。UPS選択と購入
UPSが起動しなかった理由。 恐らく老朽化だと思われる。何せ2003年購入して以来 バッテリーの交換すらしていなかったからだ。 2003年にUPSを購入した話は「システム奮闘記:その23」 (危機管理体制増強)をご覧ください。 UPSが起動しなかったという事態を重くみた上層部。 すぐに新規で購入するようにという指示が来た。 だが、基準がわからない。 そこで、昔から付き合いがあり,2003年にUPSを買ったJ社に 相談する事になった。 大まかな消費電力を伝える。 サーバー1台あたり500W これはサーバーの電源装置の最大出力なのだが これを目安にするしかない。 3台サーバーがある。合計すると1500Wになる。 その事を伝えると、以下の提案がやってきた。 1台1000WのUPSを2台購入 そして見積り金額も 業者の説明では、常時インバーター方式が、より安全なので 常時インバーター方式のUPSを勧めてきた。 でも、私には・・・ インバーターって何やねん? だった。 インバーターといえば、インバーター付エアコンなどの言葉があるが 一体、何なのかは全く知らなかった。 そんな時、隣の部署のパソコン好きの部長が 2,3万円でUPSは買えるやん! と言ってきた。 確かに、個人向けパソコン用のUPSの場合、2,3万円で買える。 安いUPSと業者が勧めてきたUPSとは、一体、何が違うのか 調べてみる事にした。すると以下のサイトを発見した。 @ITの記事だった。 電力危機を乗り切るためのキーワード 2つの違いは、UPSの電源供給の方式だった。
| 安価なUPSの仕組み |
|---|
 |
|
通常時はコンセントからの電気を直接、サーバーなどの 機器に送っている。と同時に充電を行なっている 非常時になると、スイッチが入れ替わり、バッテリーから 電力を供給する仕組みになっている。 安くい分、スイッチが切り替わる際、ほんの僅かの時間でも サーバーが落ちてしまう可能性は捨てきれない所が 問題点なのだ。 |
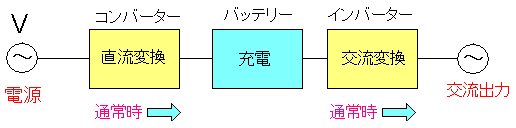
業者が提案した常時インバーター給電方式の仕組みは 以下のようになる。
| 常時インバーター給電方式のUPSの仕組み |
|---|
 |
|
コンセントから供給された電気を一度、バッテリーに送る。 そしてバッテリーの電気をサーバーなどに供給する仕組みだ。 この場合、停電が起こっても、スイッチの切り換えなどがなく 連続して電気が供給できるので、サーバーが落ちる心配はない。 その代わり、UPSの構造が複雑で高価になる問題もある。 |
この時初めて インバーターとは直流から交流に変換する装置 だと知った。 だが、この時点ではインバーター付エアコンなどを調べる気もなく そのまま放置したのだった。 さて、この2つ図だと、電気に詳しくない人でも、一目でわかる。 2つの図を使って上層部に違いを説明する事にした。 あとは、サーバーが落ちる可能性がある安価なUPSにするのか それとも高価なUPSを選ぶのかは、上に判断を任せる事にした。 結果は高価なUPSを買うように! だった。 そして業者の提案した常時インバーター供給方式を発注する事になった。 しかし、発注したものの、なかなか物が届かない。理由は・・・ タイの洪水の影響で部品供給が遅れている! だった。 タイの洪水で自動車関連や、その他、部品の供給が遅れたり 停止している事は知っていたが、まさかUPSまで影響が出ていたとは 夢にも思わなかった。UPSの設定
だが、UPSの設定を行なうのだが、UPSや電源装置について 知らない事だらけではないかと思った。 そこで少し調べようとすると、案の定、知らない言葉が出てきた。 力率って何やねん? 皮相電力って何やねん? そして一応、学生時代は理系だったのだが、社会人になってからは 事務職な上、四則演算以外は行なわないため・・・ 物理や数学なんて忘却の彼方なのだ (^^) になっている。 私が理系だったのは20世紀の話だ。 今は21世紀。未来志向の私なので、過去の話は忘却の彼方で当然なのだ。 そこで過去の記憶を呼び戻したりするため以下の本を購入した。 「絵で見てなっとく! 電気回路がよくわかる」(藤瀧和弘:技術評論社) それだけでなく、20世紀に、一応、勉強した電磁気の本なども 捨てずに置いているので、それも取り出す事にした。交流電流
直流と交流があるのだが、その違いを簡単に書いてみる。
| 直流 |
|---|
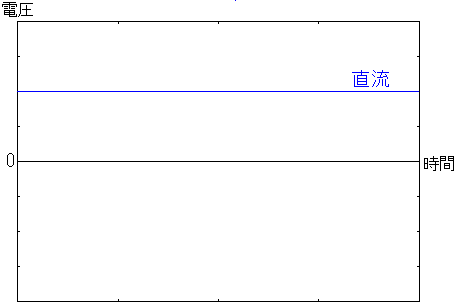 |
| 直流とは一定の電圧の電気の事を言う。 |
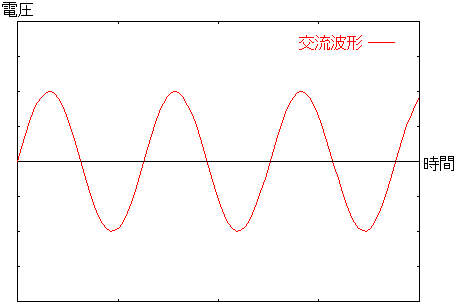
交流は以下のような波形の電気の事だ。
| 交流 |
|---|
 |
|
電圧がプラスとマイナスに交互に入れ替わる電気の事だ。 よくある交流電流は三角関数で出てくる正弦波(サインカーブ)なのだ。 今回の電気回路の勉強の中で、交流が正弦波以外に パルス型やノコギリ型の交流もあるのも知ったのだが 今回の話では割愛します。 |
三相交流
理系といっても電気工学を専攻していたわけではない上 電気工学の講義なども取った経験もない。 なので三相交流といっても 勉強した事がないのだ (^^) なので、「三相交流」という名称以外、何も知らないのだ。 そこで本を読んで見る事にした。 すると、意外にも簡単だった。 3系統の交流電流を使っているだけ なのだ。 3系統の交流電流だが、それぞれ位相を120度づつずらしている。 図にすると以下のようになる。
| 三相交流の波形 |
|---|
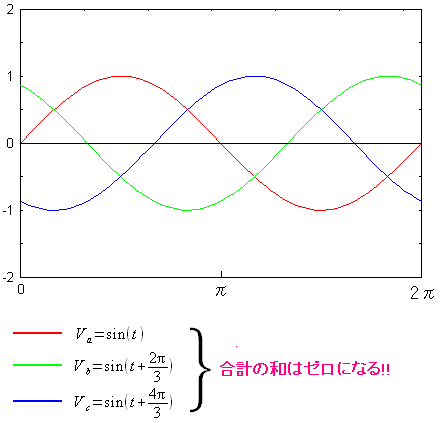 |
|
3系統の電気を通すのだが、それぞれ120度づつ位相をずらしている。 120度ずらしているのには理由があるのだ。 この3つの波形を足しあわせると、常にゼロになるのが特徴なのだ。 これが最大の利点になるのだ。 |
そして三相交流を発電所から消費地(負荷)までの回路を描くと 以下のようになる。
| 三相交流の送信と負荷 |
|---|
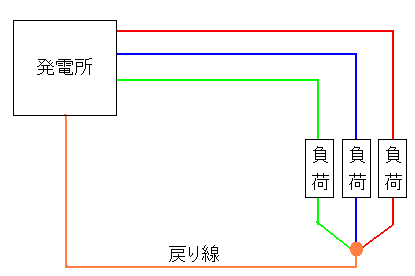 |
|
三相交流を発電所から負荷まで送る際、3系統あるので 3本の線で送電する。 戻り線は1本にしておく。 |
だが、三相交流の特徴で、3つの電気系統の波形を足し合わせると
常にゼロがある。それを考えると戻り線が不要になる。
| 三相交流は戻り線を省略できる |
|---|
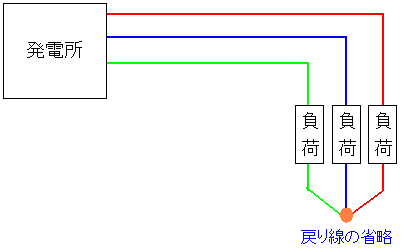 |
|
戻り線なのだが、3本の結合部分で常に電圧がゼロになる。 そのため戻り線が不要になるのだ。 三相交流で送電する理由は、3系統の電源を3本線で 送信できる事にあるのだ。 |
論より証拠で、近くの電線を見てみると3本線になっている。
| 電線を見る |
|---|
 |
電線の3本線。今まで疑問に思っていなかった。 だが、今回の三相交流を知った事で 電線の3本の理由がわかったのら (^^) ただ、一般住宅などの場合には、家屋にまで三相交流を 流しているわけではない。 電柱にあるトランス(変電器)で単層2線式(古い住宅)や 単層3線式(今の住宅)に変換されているのだ。電力の質
当たり前のように電気を使っているが、本を読んで行くと 電力に質がある事を知った。
| 電力の品質と許容範囲について | |
|---|---|
| 電圧 | 101±6が以内 95〜107Vの範囲なら安定供給というのだ。 |
| 周波数 | 西日本なら60±0.2が安定供給の目安。 |
電力に許容範囲があるとは知らへんかった
早速、コンセントから供給されている電力の状態を
見てみる事にした。
購入したばかりのUPSのWeb監視機能を使えば見れるのだ。
| コンセントから供給される電力の質 |
|---|
 |
|
電圧、周波数を見ると、許容範囲に収まっている。 時間帯が夜中なので、高めの電圧になっていると思う。 |
日本の電力会社の安定供給の凄さを感じる。 原発問題などで危機管理ができないや、原発問題の責任を取らないなど 許しがたい部分は多々あるが、安定供給の面では評価すべきだと思う。力率と電力会社
力率とは何か。 調べてみると、こういう事だという。
| 力率とは何か? |
|---|
|
交流の場合、コンデンサーやコイルの中を通したりすると 電圧と電流の間に位相のズレが生じる。 |
だから何やねん!
そこで、より踏み込んで調べてみる事にした。
どういう状態なのか、図にすると、以下のようになる。
| 電圧と電流との位相のズレが生じている状態 |
|---|
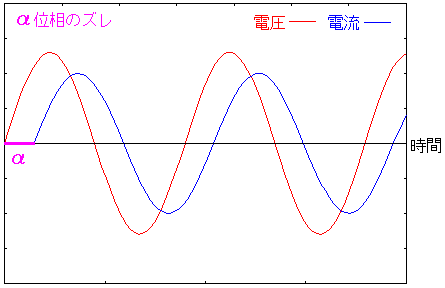 |
|
交流の場合、コンデンサーやコイルの中を通す事で 図のように電圧と電流の間の位相のズレが生じている状態が生じる。 この時の位相のズレをcosαで表す。 消費電力を式で表すと P = VI cosα になる。 「cosα」の事を力率という。 位相のズレが大きいほど力率の値が低くなる。(力率が悪くなる) |
力率が悪いと以下の事が起こる。
| 消費電力と供給電力の違い |
|---|
 |
|
力率が悪いのは、どういう事なのかを図式化してみた。 各機器が消費する電力をWとしたら、その機器の供給すべき電力は 電力「W」を力率(cosα)で割った値になる。 力率が悪ければ悪いほど、多くの電力を投入する必要が出てくるのだ。 |
ここで皮相電力の言葉の意味がわかった。
| 皮相電力と有効電力 | |
|---|---|
| 皮相電力 | 機器に供給する電力 |
| 有効電力 | 実際に機器が消費する電力 |
力率が悪いと実際に使われない無駄な電力が多くなる。 さて、電力会社が力率が悪い状態を嫌う理由が納得できる。
| 電力会社は力率が悪い事を嫌う理由 | |
|---|---|
| (1) | 電気代は有効電力分しか請求できない |
| (2) | 電気供給の際に、有効電力よりも大きい電力が必要なため 発電、送電、変電などの設備に投資がかかる |
力率が悪いと、電力利用の効率が悪いだけでなく
大電力に耐えるだけの設備が必要なため
設備投資がバカにならへん!
というわけだ。
そのため電力会社は力率向上に前向きな企業に対しては
割引料金などを提供して、少しでも力率改善に誘導しているのだ。
節電の話は、機器の消費電力を下げる事ばかり思っていたが
力率が悪いと、多くの電力を生産しないといけないため
結果的に、無駄な電力を作っている事になる。
節電には力率改善が欠かせないと思った。
ちなみに家電製品の力率だが、目安の値で、こうなっている。
| 家電の力率の値(目安) | |
|---|---|
| 蛍光灯 | 80〜90% |
| エアコン | 70〜90% |
| 冷蔵庫 | 70〜80% |
| 掃除機 | 60〜65% |
| 洗濯機 | 70〜80% |
こんなに非効率に電力を使っていたのか! で驚いた。 ところで、力率が悪くなる原因と、力率改善の話は後述しています。電気回路と電子回路の違い
今回の話は電気回路の話なのだ。 本を読み進めると、電気回路と電子回路の違いの章があった。 ふと思った。 電気回路と電子回路の違いは何やねん? 言葉では、どっちもよく聞くのだが、具体的に何がどう違うのか 考えた事がなかった。 本を読む事にした。違いは以下の通りだった。
| 電気回路と電子回路の違い | |
|---|---|
| 電気回路 | 電気を他のエネルギーに変えて 利用するための回路 (具体例) 洗濯機、ドライヤー、照明 |
| 電子回路 | 電気で信号の伝達や制御 情報の処理するための回路 (具体例) パソコン、携帯電話、テレビ |
こういう区別をしていたとは、知らなかった。
コイルと自己インダクタンスについて
モーターや変圧器などにはコイルが使われている。 コイルについて、簡単に話を書きたいと思います。ソレノイドコイルと磁場の関係
電気回路の入門書でコイルの話はでてくるし、モーターなどにも コイルが使われている。
| コイルの誘導起電力 |
|---|
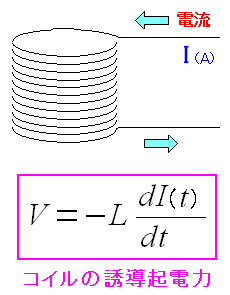 |
|
コイルに流れる電流が変化すると、起電力が発生する。 その時の比例定数(L)を自己インダクタンスと呼ぶ。 |
この式を当てはめると、計算はできる。 でも、コイルで何が起こっているのかを知らないと 電気回路や電子回路を組めなくなる。 そこで、私の復習という事で、電磁気学の初歩の勉強する事にした。右ネジの法則とアンペールの法則
学生時代は理系だった私。昔、昔に電磁気学習ったのだが 忘却の彼方なので、最初からの勉強になる。 電線に電気を流すと周囲に磁場が発生する。
| 「磁場」と「磁界」の違いについて |
|---|
|
2つとも同じ意味なのだ。単なる名称の違いにすぎない。 物理系の人は「磁場」と呼んでいるが、 工学系の人は「磁界」と言うだけの違いだ。 「車」と言うか、「自動車」と言うかの違いと同じだ。 |
磁場の方向を示す法則として、右ネジの法則がある。 図にするとこういう事だ。
| 右ネジの法則 |
|---|
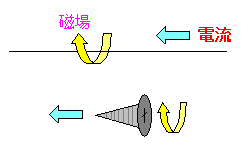 |
|
電流の向きと、電流によって発生する磁場の向きを表した法則だ。 右ネジを使うと上手に表現できるために、右ネジの法則と 言われていると思われる。 |
そして電流によって、電線の周囲を回転する磁場が生まれる。 電流と磁場の関係はアンペールの法則で表わせるのだ。
| 磁界の強さ:アンペールの法則 |
|---|
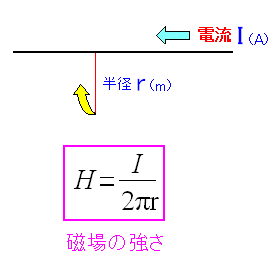 |
ところで磁場を考える際、磁場と磁束密度の2つが存在する。 よく電磁気では磁束密度が使われる。 アンペールの法則で見てみると、次のようになる。
| アンペールの法則 |
|---|
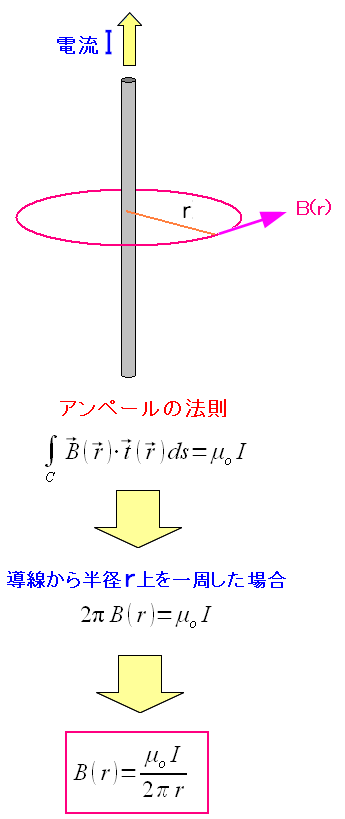 |
|
よく使われるアンペールの法則だ。 電流が貫く閉曲線上の磁場を足していった場合 電流と電流が作り出す磁束密度の関係式だ。 「μo」は、真空中の透磁率になる。 |
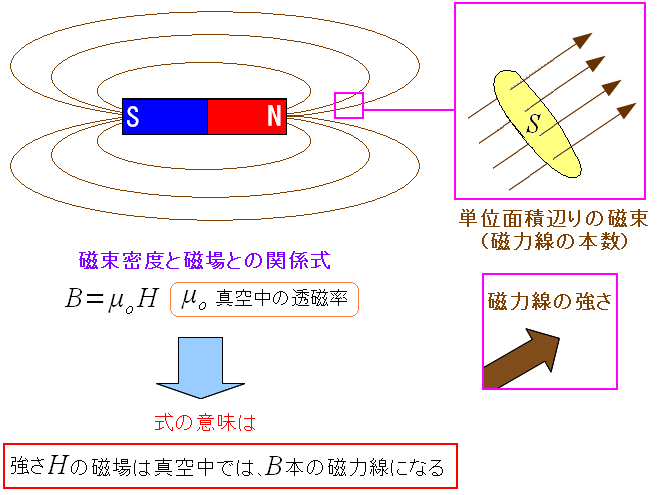
ところで・・・ 磁場と磁束密度の違いは何やねん? になる。 この違いは 磁場は磁力の強さ 磁束密度は単位面積辺りの磁力線の数 なのだ。 磁場と磁束密度を結びつける係数が透磁率なのだ。
| 磁場と磁束密度の違いと、その関係式 |
|---|
 |
|
磁場(磁力の強さ)と、磁束密度(単位面積辺りの磁力線の本数)の関係式だ。 透磁率は物質によって異なる。 磁場に、透磁率の係数をかけると、磁束密度が求まる。 |
ここで正直に書くが、実は磁場と磁束密度の違いがわかっていなかった。 そのため、この章の初版では、以下のようなデタラメな事を書いていたのだ。
| 改定前のデタラメな記述 | |||||||||
電流が作り出す磁場の強さなのだが、そのままでは使えない。 磁場の強さ(H)は、あくまでも何も考慮されていない場合の状態だ。 だが、物質の中を通過する場合、物質によって磁力線の強さは異なる。 そこで各物質内に対応した磁力線の強さを求めるのが一般的になっている。
磁場の強さと、磁束密度の違い。
非常にわかりにくいのだ!!
でも、私は次のように考えたのだ。
こんな事を書くと専門家から デタラメ書くな! と言われるかもしれないが、ハッキリ言う。 私が勝手に考えた物と明記しているだ! (^^) 受け手の誤解のないように明記しているので、それで良いのだ。 だが、いい加減な事を書いているのは良くないので 磁束密度の定義を書く事にした。
|
2012年に、この話を書いた時、全くわかっていなかったのが露呈された。 でも、2015年から1年かけて電磁気学の勉強をしなおした結果 正しい知識を身につける事ができた。 詳しくは「システム奮闘記:その105」(電磁気学の基礎 電磁気学入門)をご覧ください。
磁束密度とコイルの関係
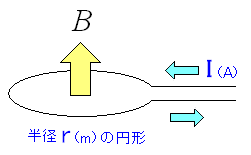
さて、磁界と磁束密度の関係がわかった所(?)で、 コイルに電流を流した場合に発生する磁場の話に進みます。 まずは、円形の回路を考えてみる。
| 円形の回路の磁束密度を考える |
|---|
 |
|
円形の回路にした場合、真ん中を突き抜ける磁束密度は いくらになるのか考えてみる。 |
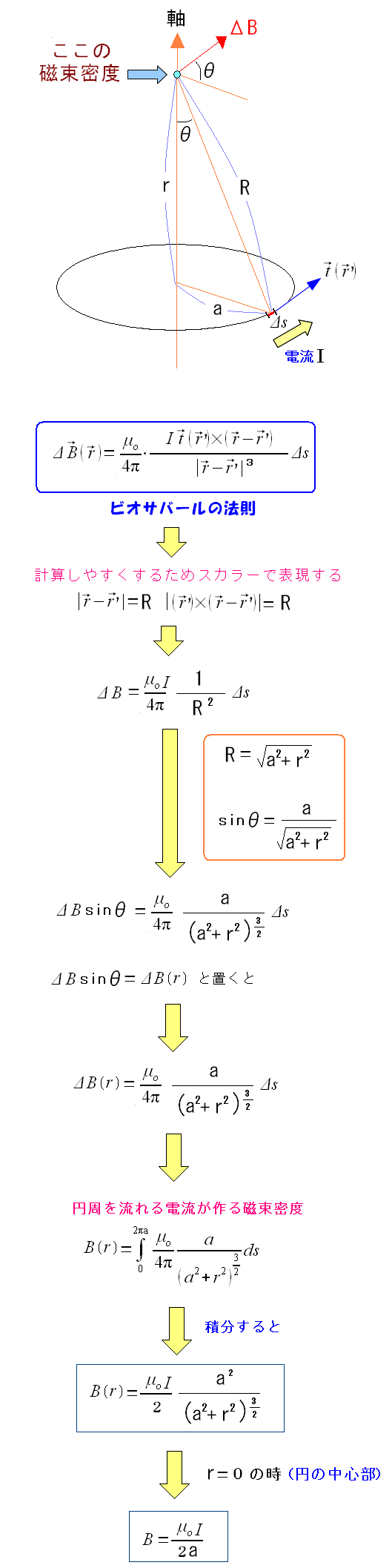
円形の線の各部分から発生する磁束密度なのだが これを合計すると、どれくらいの力になるのか計算してみる。
| 円形回路の中の磁束密度の計算 |
|---|
 |
|
アンペールの法則ではなく、ビオサバールの法則を使って導いた。 詳しくは「システム奮闘記:その105」(電磁気学の基礎 電磁気学入門)をご覧ください。 |
正直なことを書くと、この章を書いた2012年当時、ビオサバールの法則なんて 理解していなかった。 そして磁束密度と電流の関係のアンペールの法則も理解していなかった。 そのため以下のようなデタラメな記述を平気でしていたのだ。
| 改定前のデタラメな記述 | |||
円形の線の各部分から発生する磁束密度なのだが これを合計すると、どれくらいの力になるのか計算してみる。
|
2012年当時、何もわかっていない事が露呈されただけでなく わけのわからん事を書いている事も露呈された。 あえて自己弁護すると、わからんなりにも必死に書いていたと思う。 さて、ソレノイドコイルから発生する磁束密度を考える。
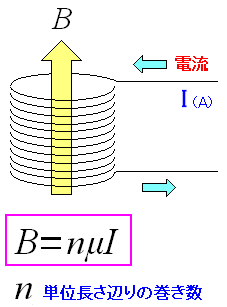
| ソレノイドコイルから発生する磁束密度 |
|---|
 |
|
磁束密度の強さはソレノイドコイルの単位当たりの巻数に依存する。 だが、この説明は、ここでは省略します。(※) |
上の説明の部分で(※)をつけた。 正直に書くと、この章を書いた時は 説明できるだけの知識があらへんかった!! なのだ。
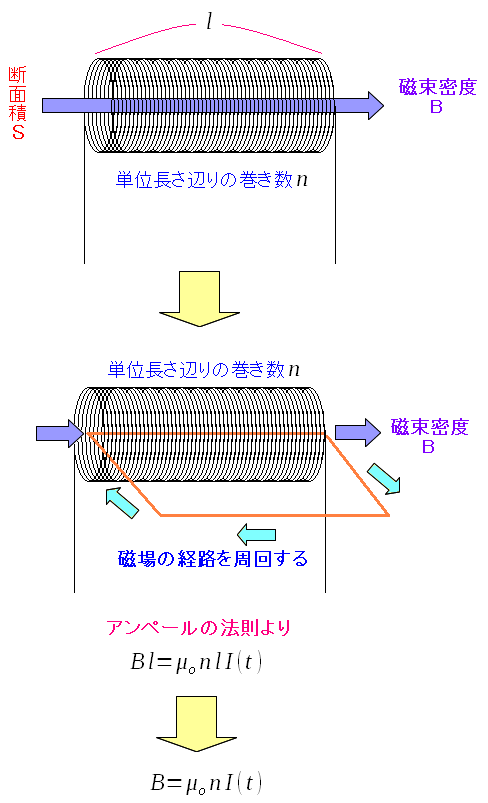
| コイルの中を貫く磁束密度の式の求め方 (2016年5月追加) |
|---|
 |
|
アンペールの法則とは、電流が貫く閉曲線の磁束密度を足しあわせた時の 電流と磁束密度の関係式になる。 上図の閉曲面の場合、閉曲面を貫く電流は「電流×コイルの巻き数分」になる。 コイルの単位長さ辺りの巻き数を「n」としてコイルの長さを「l」にすると アンペールの法則から、コイルの中を貫く磁束密度が求められるのだ。 |
レンツの法則とファラデーの電磁誘導の法則
ここまでは電線に電流を流すと磁場が発生する話を書きました。 ここからは反対に、磁場が電流を発生させる話を書きます。 まずは磁束の説明だ。
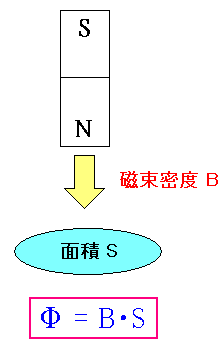
| 磁束とは |
|---|
 |
|
磁束とは上図のように、ある領域を突き抜ける磁力線の度合だ。 磁束密度(B)と面積(S)の積で表される。 |
レンツの法則とは、回路に磁束の変化が起こると、その変化を 抑えようとする働きの事を言う。
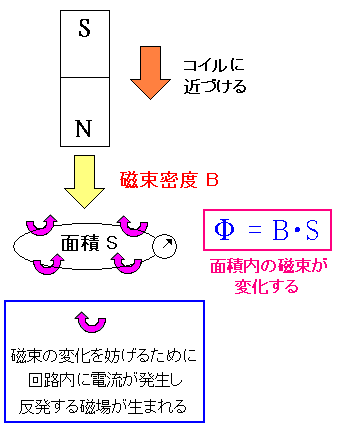
| レンツの法則 |
|---|
 |
|
磁石を回路に近づけると、磁束が増加(変化)する。 そこで自然界は、磁束の増加を抑えようとする働きが発生する。 上図の回路の場合だと、磁束の増加を抑えるため 回路に電流が発生し、電流が作る磁界が反対向きに発生し 磁束の増加を抑える働きをする。 |
人間界では、何か改革を行なおうとすると 必ず抵抗勢力が現れる! 自然界でも、何か変化が起ころうとすると 変化を抑える現象が働く! 妙な類似点を感じてしまった。 ところで、レンツの法則は変化を抑える現象が働くという定性的な事だが それを定量化したのがファラデーの電磁誘導の法則だ。
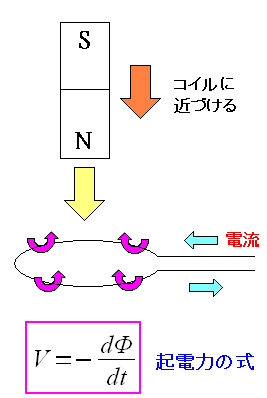
| ファラデーの電磁誘導の法則 |
|---|
 |
|
ファラデーの法則とは、磁束の増加(変化)に伴い それを抑えるために発生する起電力との関係式なのだ。 上の式は、磁束の変化量に比例して、起電力が発生する意味だ。 |
だが、2012年の段階では、ファラデーの電磁誘導とレンツの法則の違いを きちんと把握していなかった。
| ファラデーの電磁誘導とレンツの法則の違い (2016年5月追加) |
|---|
|
ファラデーの電磁誘導は、コイルの中に磁石を入れると 磁束が増加するに伴い、起電力が発生し、電流が流れる事を発見したのだ。 レンツの法則は、その電流の向きが、増加する磁束を食い止める向きに 流れる事を発見したのだ。 言い換えると、磁束を減らす向きに電流が流れる事を発見したのだ。 電磁気の歴史で見ると、先にファラデーの電磁誘導が発見され その後、レンツの法則が発見されたのだ。 |
ところで「ファラデーの法則」を言う場合、注意が必要だ。 なぜなら2つあるからだ。
| 2つあるファラデーの法則 |
|---|
|
ファラデーの法則は2つある。電磁誘導と電気分解だ。 この2つを区別するために、電磁気でのファラデーの法則を 「ファラデーの電磁誘導の法則」を呼んでいる。 |
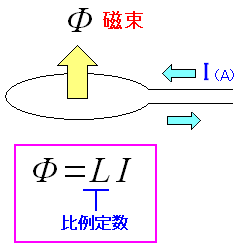
自己インダクタンス
自己インダクタンス。 ただの定数なのだ。
| 閉じた回路における磁束と電流の関係式 |
|---|
 |
|
閉じた回路の中で電流を流すと、それに比例した磁束が発生する。 この時の比例定数「L」が自己インダクタンスになる。 「なぜ、こんな関係式が出てくるの?」と聞かれても 「自然に聞いてくれ」としか答えられない。 自然の振る舞いが、たまたま上の式に当てはまったにすぎないからだ。 |
コイルの誘導起電力の式を導く
Φ = LI 上の関係式を微分してみる。 双方の変化量の比例関係が見れるのだ。
| 磁束と電流の関係式を時間で微分する |
|---|
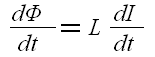 |
| 時間で微分する事で、磁束の変化量と電流の変化量の関係が出てくる。 |
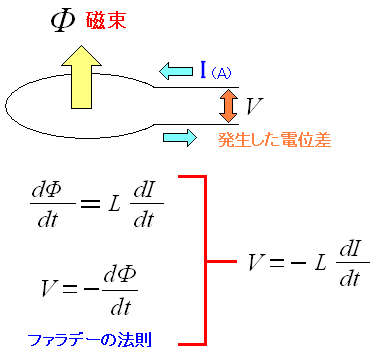
上の式とファラデーの誘導起電力の法則を照らし合わせる。
| ファラデーの誘導起電力の法則を照らし合わせる |
|---|
 |
|
閉回路の電流の変化量と、発生する起電力(回路の電位差)との 関係式が導ける。 |
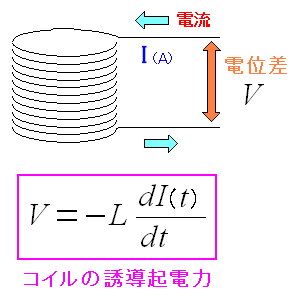
コイルも閉回路なので同様の事が成り立つ。
| コイルで発生する誘導起電力の式 |
|---|
 |
|
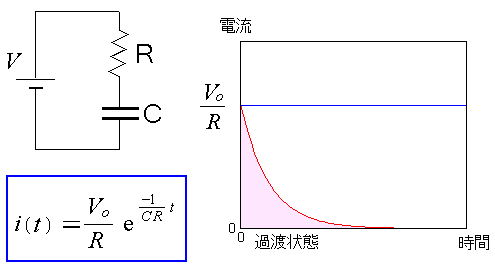
コイルに流れる電流が変化した場合、コイルの両端で電位差が生じる。 比例定数を自己インダクタンスと呼ぶ。 もちろん、直流電流の場合、電流は一定のため電流が変化しないため 電位差も生じない。 厳密に書くと、直流電流でも電源を入れた瞬間は、電流が変化するため コイルに電位差が生じる。電流が一定になると電位差がなくなる。 電流が一定になるまでの間を「過渡状態」という。後述しています。 |
これでコイルの話の準備はできた。
コンデンサー
次にコンデンサーの話を書く事にします。 式だけ書くと簡単だ。
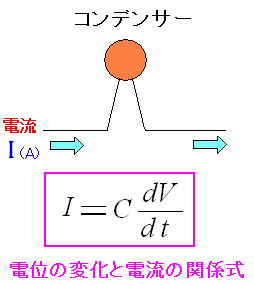
| コンデンサーの電位の変化と電流の関係 |
|---|
 |
|
コンデンサーの両端の電位が変化すると それに比例した電流が流れる。 比例定数になっているCは、電気容量で 1(V)当たり、コンデンサー内に、どれくらい電気が 溜められるかの値だ。 |
だが、どうして、この式になるかを知らないと 計算ができなくなるので、私の復習をかねて 再び電磁気学の勉強をする。コンデンサーの仕組み
コンデンサーは電気を溜める役割を果たす。 構造そのものは単純だ。
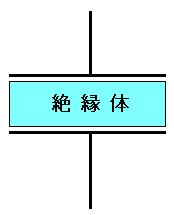
| コンデンサーの構造 |
|---|
 |
|
コンデンサーの中は、電極の間に絶縁体が入っている。 電解コンデンサーなどは、もう少し複雑になる。 |
そこに直流電流を流すと以下の事が起こる。
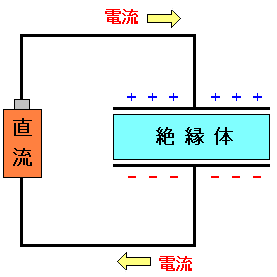
| コンデンサーに直流電流を流す |
|---|
 |
|
電流を流すとコンデンサーの片方にはプラスの電荷。 片方にはマイナスの電荷が溜っていく。 コンデンサーに電荷が満杯に溜ったら、電流が流れなくなる。 コンデンサーは直流電流が流れないと言われる理由だ。 |
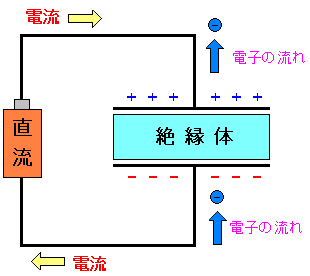
ここで厄介なのは電流の方向と電子の流れの方向が正反対な事だ。
| 電流の方向と電子の流れの方向が正反対 |
|---|
 |
|
電子が移動する事で、コンデンサーの両極に電荷を帯びるのだが 電流の方向と電子の方向が正反対なのだ。 これは慣れるしかないのだ。 |
電子と電流の方向が正反対なのは、電気回路や電子回路を 学ぶ人にとって最初の鬼門だと思う。 以下の歴史的背景があったからだ。
| 電子と電流の方向が正反対な理由 |
|---|
|
電子の流れがわかっていない時代の話に遡る。 電気が流れているが、どういう方向に流れているのかわからない。 そこでプラスからマイナスに電流が流れると定義された。 その後、電子がマイナスからプラスに流れる事がわかった。 だが、後の祭りだった。そして、今更、変更すると混乱を招くという事で 電流の流れと電子の流れが正反対のまま、今に至っているのだ。 |
電場とは何か?
コンデンサーに電気が溜る仕組みを知るためには 電場の話を知らなければならない。 というわけで私の復習をかねて書くことにした。
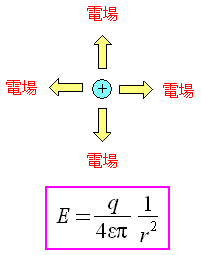
| 電場とは |
|---|
 |
|
荷電粒子が作り出す空間の状態を電場という。 電場の強さを式で表す事ができる。 |
でも、これだけだと電場が何かピンと来ない上に 電場の強さといっても、何かのかが掴めない。 ところで荷電粒子同士、力を及ぼし合っている。 双方とも同じプラス(マイナス)なら反発し合う力が働き 異なる場合だと引きつけ合う力が働く。
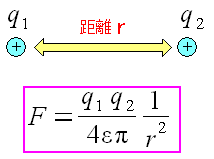
| 荷電粒子同士が及ぼす力 |
|---|
 |
|
反発(もしくは引きつけ合う)力は、荷電粒子の電荷に比例し 距離の2乗に反比例する。 |
荷電粒子同士が反発したり、引きつけ合ったりするのは 電場が作用しているからだ。 そこで力と電場の関係式は以下のようになる。
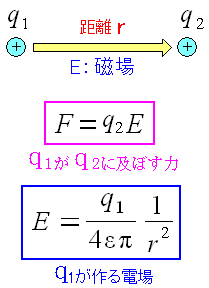
| 力と電場の関係 |
|---|
 |
|
荷電粒子「q1」が空間に作り出す電場Eと 電場Eが「q2」に作用して、力Fが働く。 |
つまり・・・ 電場とは電荷が作る空間の状態 なのだ。 そして電場は・・・ 相手の荷電粒子に力の作用を及ぼす のだ。 さて、回路に平行板をおいた場合、以下のようになる。
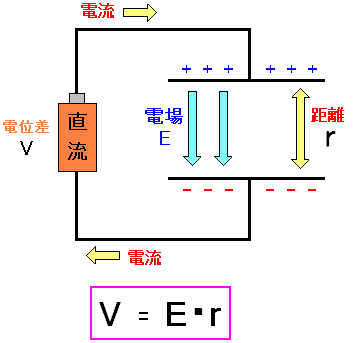
| 平行版を置いた場合 |
|---|
 |
|
プラス側の板とマイナス側の板の間には電場が発生する。 電場の強さは、電圧と板と板との間の距離に依存する。 両極の板に電荷が溜るので、コンデンサーの原型になるのだ。 |
だが、これでは溜められる電気の量が少なすぎるため そこで極版の間に絶縁体を挿入するのだ。
| 極板の間に絶縁体を挿入する |
|---|
 |
|
より多くの電気を溜めるために極版の間に 絶縁体を挿入しているのだ。 |
なぜ、絶縁体を入れると電気が溜りやすくなるのか。絶縁体と分子。分極
絶縁体を使う理由。電気を流さないのが理由なのだが 絶縁体の中で何が起こっているのかを見てみる事にする。 ところで物質は分子でできている。 決して、原子や素粒子という突っ込みをしないように! 身近な水分子の構造をみてみる。
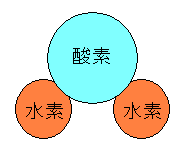
| 水分子 |
|---|
 |
|
水分子は水素と酸素原子で構成されている。 団子のように綺麗に並んでいるのではなく 三角型になっている。 |
さて、三角型になっているため、以下の事が起こる。
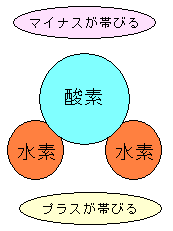
| 水分子の分極 |
|---|
 |
|
水素、酸素は合計すると電荷はゼロなのだが 形状が三角形になっているため 電荷に偏りができてしまう。この偏りを分極という。 踏み込んで書くと双極子モーメントの話になってくるのだが そこまで勉強する気力はないので割愛します (^^) |
だが、水にしても普通の物質にしても分極していない。 電気的に中性なのは、以下の通りなのだ。
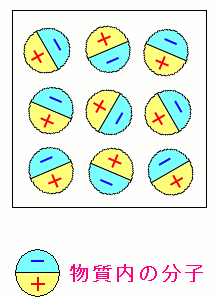
| 水や物質が普通の状態では電気的に中性な理由 |
|---|
 |
|
分子は物質内ではバラバラの向きに存在する。 その結果、平均化されて、中性の状態になっているのだ。 |
だが、電場をかけると状況は一変する。
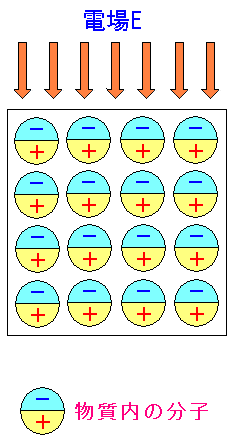
| 電場をかけると分極する物質 |
|---|
 |
|
電場をかけると、物質内の分子の向きが電場に作用される。 そのため、上図のように個々の分子が一定の方向を向くようになる。 |
さて、コンデンサーの場合を見てみる。
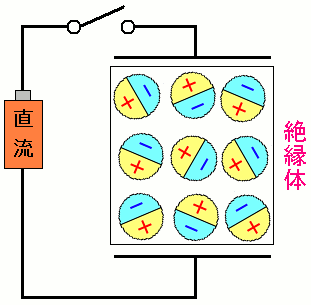
| 電気を流していない場合 |
|---|
 |
|
コンデンサーに電気を流す前は、電位差が生まれないため 電場も発生しない。そのためコンデンサーの中の絶縁体は 分子の並びはバラバラで、結果的に中性になっている。 |
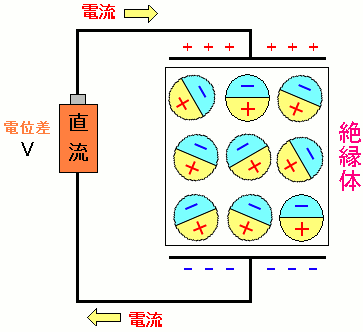
そして電気を流し始めると電位差が生じて電場が発生する
| 電気を流し始めた場合 |
|---|
 |
|
電気を流し始めると電位差が生じ、電場が発生する。 それに伴いコンデンサーの中の絶縁体内の分子の向きが 一定の方向を向こうとし始める。 |
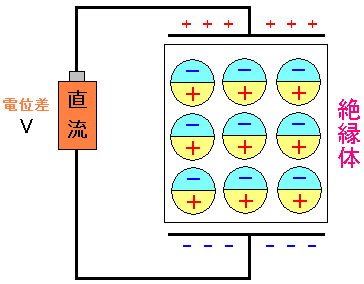
そして電気が流れなくなる充電完了状態になると 以下のようになる。
| コンデンサーの充電完了の様子 |
|---|
 |
|
コンデンサー内の分子の向きが同じ方向を向いた時が充電完了だ。 そして電気が流れなくなるのだ。 |
コンデンサーの仕組みを勉強した気になるのだが ここで終わると 極板の間に絶縁体を入れたら より電気が溜めれる理由を説明していない なのだ。 放置するわけにはいかないのだが・・・ イマイチよくわからんのだ 直感的に「なるほど」と思うような説明が見つからない。 というわけで、わかったような、わからんような説明になるが それについて書いてみる事にした。ガウスの法則
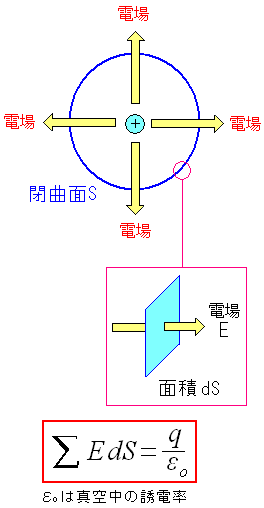
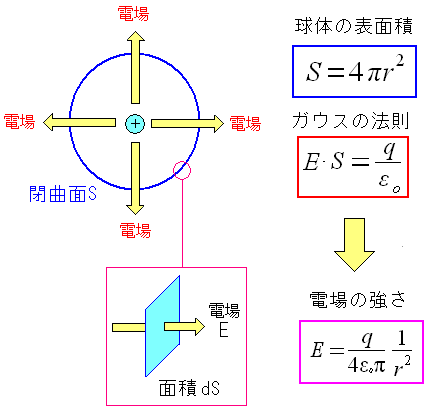
ガウスの法則とは、荷電粒子と、それが生み出す電場の量の関係だ。 荷電粒子を球体で囲んだ例を考える。
| ガウスの法則 |
|---|
 |
|
ガウスの法則を考える時、電場を束だと思えば良いのだ。 荷電粒子が作る電場の束は、荷電粒子の電荷量に比例する。 これがガウスの法則だ。 赤く囲んだ式は、ある面積を突き抜ける電場の束を集めた場合 その合計値が、荷電粒子の電荷量に比例するという意味だ。 |
ガウスの法則を使って、荷電粒子が作り出す電場の大きさを 算出してみる事にした。
| 荷電粒子が作り出す電場の大きさ |
|---|
 |
|
球体の表面を突き抜ける電場は一定なので 球体の表面積と、ガウスの法則の式を組み合わせると 電場の大きさの式が導き出される。 まさに荷電粒子が作る電場の強さの式なのだ。 |
狐に包まれた感覚なのだが、これがガウスの法則なのだ。 ガウスの法則が何かわかった(?)ところでコンデンサーを見てみる。
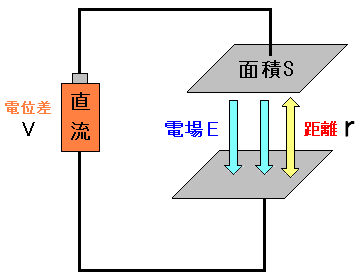
| コンデンサーの極板に何も入れない時 |
|---|
 |
|
両方の極板の間に電場「E」という強さで 極板と極板の間の距離を「r」とする。 |
さて、ガウスの法則を使って考えてみる。
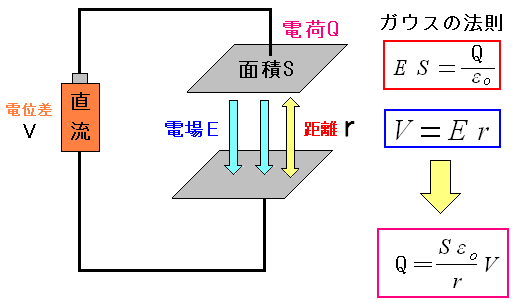
| 極板間の電場の強さを考える |
|---|
 |
|
ガウスの法則は荷電粒子が作り出す電場の束の合計が 電荷に比例しているので、上の赤く囲んだ式になる。 そして電場と距離との積が電位になるので その2つの式を組み合わせると、電荷と電圧の関係式が出てくる。 極板の面積、極板同士の距離、誘電率は一定なので 電圧と電荷の比例式になる。 |
さて、電圧と電荷の比例式を、じっくり見てみる。
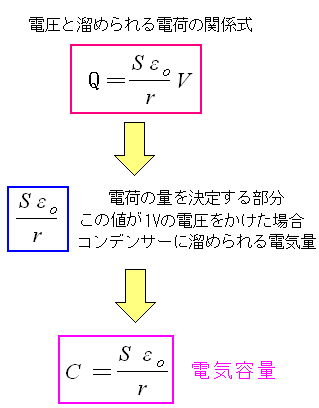
| 電圧と電荷の比例式 |
|---|
 |
|
電圧と電荷の間に成り立つ式が出てきた。 係数を構成する面積、距離、誘電率は定数で一定の値になる。 この値は、1V当たりにコンデンサーに溜められる電荷量になる。 これを電気容量と呼び、記号「C」で表すのだ。 |
コンデンサーを考える上での大事な公式
Q = CV
が導けた。
さて、1V当たりにコンデンサーに溜められる電気容量が求められた。
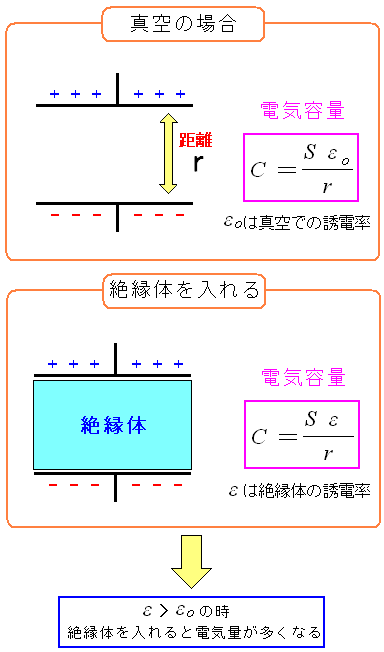
ここからなのだが、誘電率は物質によって異なる。
| 誘電率の違いで電気容量が変わってくる |
|---|
 |
|
真空の場合の誘電率と、絶縁体の誘電率は同じではない。 もし、絶縁体の誘電率の方が高い値を取れば、絶縁体を入れた場合の 電気容量が大きくなり、より多くの電気を溜める事ができるのだ。 |
ようやく絶縁体を中に入れた方が電気が溜められる事が説明できた。 ちなみに電気容量を表す「C」はCapacityに由来している。コンデンサーの問題を解く式
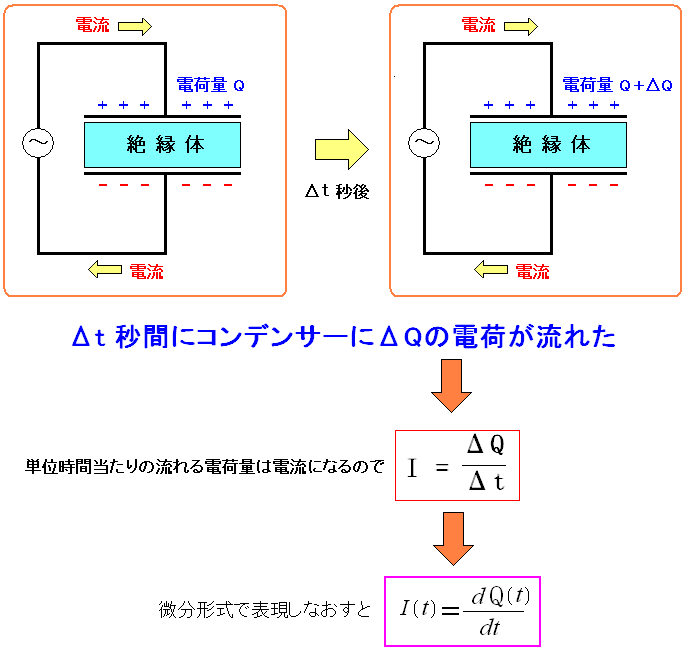
コンデンサーを入れた回路の問題を解く場合を考える。 必要なのはコンデンサーの電位と、コンデンサーに流れる電流の関係式だ。 まずはコンデンサーに溜った電荷量と電位と電気容量の関係式の Q = CV は出てきた。 だが、このままではコンデンサーに流れる電流がわからない。 そんな時、コンデンサーを流れる電流の求め方を考える。 電流とは単位時間当たりに流れる電荷の量 なのだ。
| コンデンサーに流れてくる電荷を見てみる |
|---|
 |
|
ここでは、まずコンデンサーに溜る電荷量の変化を見る。 単位時間での電荷の量は「電流」になるため上のような式が成り立つのだ。 |
そして「Q = CV」の式とを組み合わせる。
| コンデンサー内の電位と電流との関係式 |
|---|
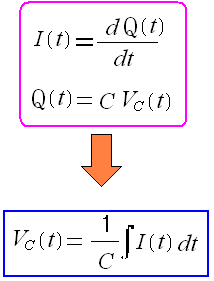 |
|
見事のコンデンサー内の電荷の「Q」を消す事ができた上 電位と電流の関係式が導けた。 |
この関係式を使って、回路の問題を解くのだ。
| 「Q = CV」の覚えかた |
|---|
|
高校時代の物理の先生が言った公式の覚え方だ。 キューはシーブイ 俺は渋い! 意味不明のオヤジギャグなのだが、いまだに頭にこびりついている。 「F = qE」の覚え方も「力で絞め上げるとクイーと叫ぶ」だ。 オヤジギャグと物理の公式の親和性はあるのかなぁと思ったりする。 アニメ・涼宮ハルヒの原作者の谷川流さんも この先生の物理の授業を受けている可能性はあるので ハルヒの作品に何らかの影響はあるのかもしれないと 勝手に推測する。谷川流さんは私の高校の先輩に当たる人だ。 英語の先生でoccupyの覚え方は「お父ちゃんは、お母ちゃんの オッパイをオキュパイする」と言っていた先生もいたが この先生が赴任する前に谷川流さんは卒業しているので ハルヒの作品への影響はないと思う。 |
抵抗器
コイル、コンデンサーの説明をしたが抵抗器の説明がなかったので 簡単に説明します。
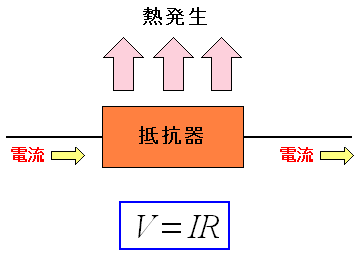
| 抵抗器 |
|---|
 |
|
抵抗器の中には、電気を通しにくい物質が入っている。 電気の流れにくさの値としてオームが使われる。 上図の青く囲んだ部分は、オームの法則だ。 電気が抵抗器を通過する際、電気エネルギーの一部が 熱エネルギーに変換される。この時、発生する熱の事を ジュール熱と呼ぶ。 |
電気が流れにくい物質(抵抗値オームの値が大きい物質)を応用したのが ニクロム線などを使った熱発生装置なのだ。 ちなみに抵抗のRはResistanceから由来している。電力消費をする抵抗。電力消費をしないコンデンサーとコイル
電力消費をする抵抗。 これは非常にわかりやすい。 電気エネルギーを熱エネルギーに変換して放射 しているのだ。 そのため熱エネルギー分だけ電力を消費した事になるのだ。 さて、コンデンサーとコイルが電力消費をしないという。 どういう事なのか? そこで、まずはコンデンサーを見てみる。
| コンデンサーだけの交流回路 |
|---|
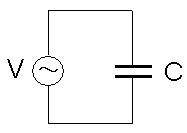 |
| ここに交流電流を流してコンデンサーが電力消費するかを確かめる。 |
まずはコンデンサーに流れる電流と電圧を計算する。
| コンデンサーに流れる電流と電圧 |
|---|
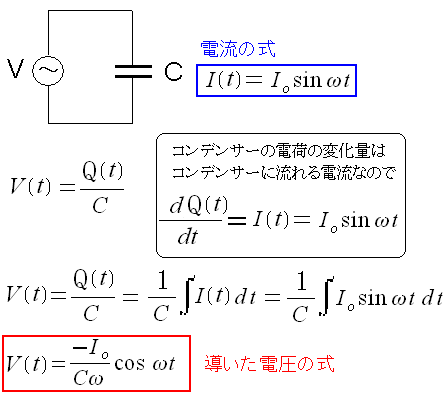 |
電圧と電流が求められたので、コンデンサーがする電力消費を 求める事ができる。
| コンデンサーが消費する電力 |
|---|
 |
| 計算の結果、コンデンサーは電力消費をしない事がわかる。 |
でも、式の上では電力消費をしない事がわかっても
一体、コンデンサー内では何が起こってるねん!
と思う。
そこで、簡単に図にしてみた。
| コンデンサー内で起こっている現象 |
|---|
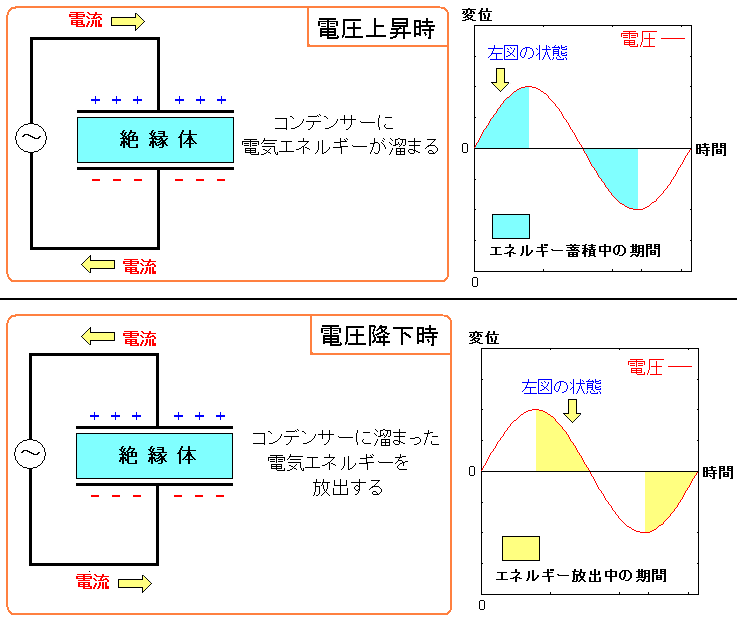 |
|
電圧を上げてコンデンサーに電荷を運んでいる間は コンデンサーに電気エネルギーが蓄積される。 そして電圧を下げると電気が溜められなくなるため 溜った荷電が回路に戻されるのだ。 電気エネルギーの放出なのだ。 |
コンデンサーに電気を溜めては放出する
その繰り返しなので、コンデンサーは電力消費をしないという事だ。
次にコイルについて見る事にする。
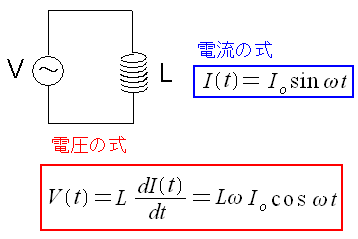
| コイルだけの交流回路 |
|---|
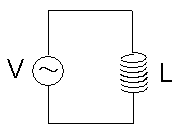 |
| ここに電気を流してコイルが電力消費をするかどうかを計算してみる。 |
コイルにかかる電圧と電流を計算する。
| コイルにかかる電圧と電流を計算 |
|---|
 |
そしてコイルがする消費電力を計算する。
| コイルがする仕事を計算 |
|---|
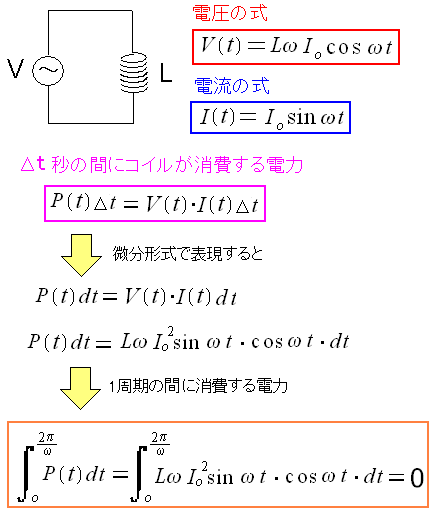 |
| 計算の結果、コイルは電力消費をしない事がわかる。 |
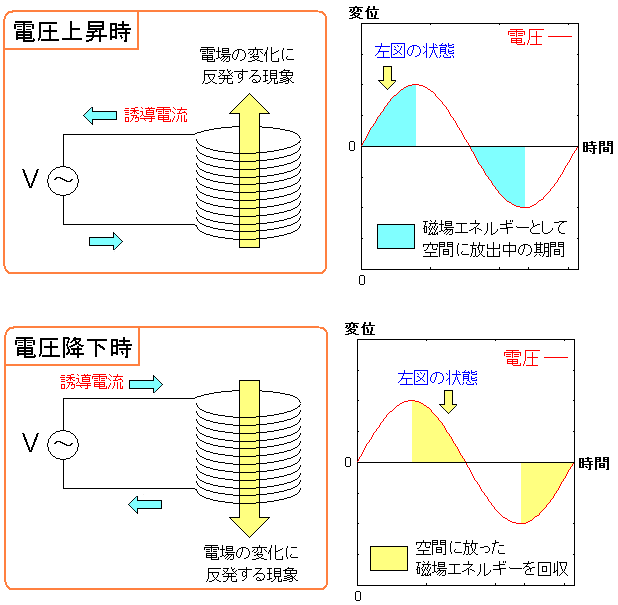
計算ではコイルは電力を消費をしない事がわかっても ピンと来ないので、図にしてみる事にした。
| コイル内で起こっている現象 |
|---|
 |
|
コイルに電圧をかけると、コイル内の磁場の変化を食い止める働きとして 誘導電流が発生し、変化とは反対方向の磁場が発生する。 この時、電気エネルギーが磁場のエネルギーとして放出される。 そして電圧を下げると、磁場が変化するため、それを食い止める働きで 今度は、反対方向に誘導電流が発生し、磁場が発生する。 この時、磁場のエネルギーを回収している。 |
わかったような、わからんような説明になったのだが
コイルの場合、上手に説明できへん (--;;
なのだ。
| 2016年5月に加筆 | |||||||||
この話を書いた当時は、磁場のエネルギーはどこに行ったのかを 理解していなかったため、説明ができなかった。 ファラデーの電磁誘導の微分形と、ポインティングベクトルを使えば 磁場のエネルギーはどこにあるのかがわかる。 ファラデーの電磁誘導の微分形とポインティングベクトルについては 「システム奮闘記:その105」(電磁気学の基礎 電磁気学入門)をご覧ください。
電磁エネルギーはポインティングベクトルを見れば エネルギーの流れの方向がわかるのだ。
電気エネルギーがコイルの中心に溜まっていくというのだ。 この時、コイルに溜まった磁場のエネルギーだが 単位体積辺りのエネルギーは以下の式で表わせるのだ。
コイルの中(空間中)に電気エネルギーが蓄積されていくというわけなのだ。 |
電気回路の計算 微分積分を使った解法
ようやく回路の話に入る事ができた。 コンデンサー、コイル、抵抗を使った簡単な回路を考える事にした。RL直列回路 交流編
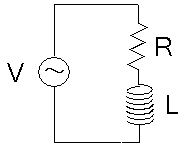
RL直列回路を見てみる事にした。 ところでモーターなどの動力を使うと力率が悪くなる。 モーターの中身はコイルだ。そのため・・・ モーターはコイルと考えれば良いのだ! 実際に、力率が悪くなるのを確かめるのに、 RL直列回路を使って考えてみる事にした。
| RL直列回路 交流 |
|---|
 |
|
抵抗とコイルが直列につながった回路だ。 モーターはコイルに置き換えて考える事ができる。 |
さて、回路の中を流れる電圧と電流を計算する事にする。 てっとり早い方法として、微積分を使って解く事にした。
| 電気回路の式を解く方法について |
|---|
|
微積分を使う以外に、複素数を使って解く方法や ラプラス変換を使って解く方法もある。 だが、この時、複素数を使って解く方法や ラプラス変換を使う方法は知らなかったので 過去の記憶を辿れる微積分を使った方法にした。 学生時代、電気工学、電子回路、制御工学を学んでいない上 その手の講義を受けていないので、全く知らなくても当然なのだ (^^) |
手始めに各部分の電圧を求めてみる事にした。
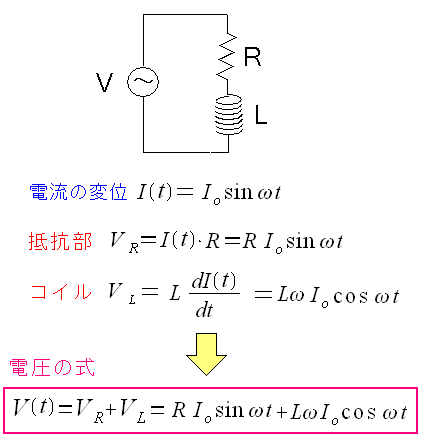
| 各部分にかかる電圧を算出してみる |
|---|
 |
|
抵抗、コイルにかかる電圧を求めてみる。 交流電流なので、電流の変移は三角関数で表現できる。 コイル部分だが、電流を微分すれば良いのだ。 とはいえ、私自身が三角関数の微分は学生時代以来なので 忘却の彼方から思い出しての作業になった。 |
回路全体の電圧が導き出せたのだが、これでは見にくい。
もっと、すっきりした形にできるはずだ。そこで思い出す。
三角関数って合成できたやん!
とはいえ三角関数の合成関数の公式なんて忘却の彼方なので
ネットで調べて思い出す事にした。
| 回路の電圧計算の結果 |
|---|
 |
|
算出された電圧の変位が正弦波(サインカーブ)になる事がわかる。 それと同時に位相のズレがα分、生じるのがわかる。 これが力率を悪くしている正体だ。 |
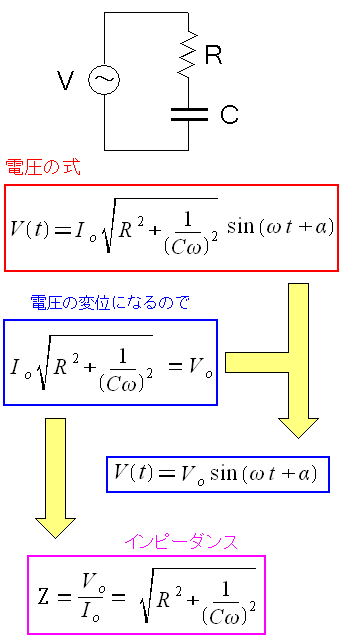
そしてインピーダンスを求める。
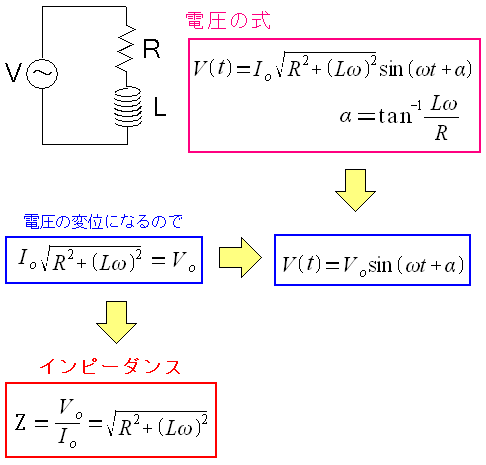
| RL直列回路のインピーダンス |
|---|
 |
|
赤く囲んだ部分はインピーダンスだ。 この時は気づかなかったが、角速度が大きくなれば インピーダンスも大きくなる。これを応用したのが ローパス回路なのだ。 |
ところで インピーダンスとは何やねん! 電気回路の話なんて忘却の彼方。 高校や大学の電磁気で習っていても、社会人になってからは 電磁気や回路なんて触った事がないだけに、覚えているわけがない。 調べてみると 電気の流れにくさ だった。 さて、位相のズレ「α」について見てみる。
| 位相のズレ「α」について |
|---|
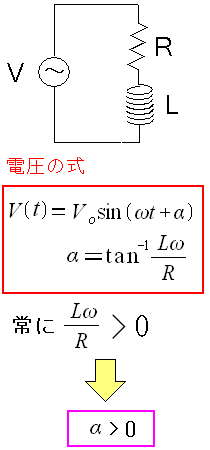 |
| 常に位相のズレ「α」が正の値を取る事がわかる。 |
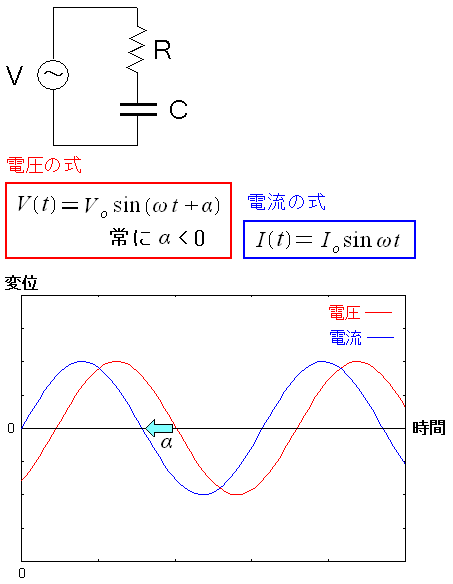
そして電圧と電流の変位をグラフにしてみた。
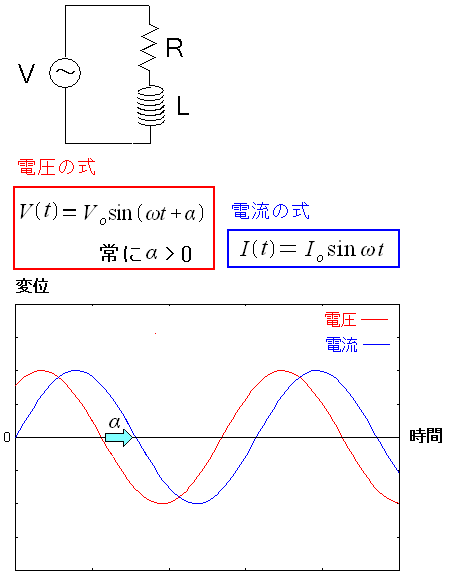
| 電圧と電流の変位をグラフ |
|---|
 |
|
電圧の正弦波と電流の正弦波を比較すると 電流の正弦波が「α」分、遅れているのがわかる。 これにより、コイル(モーター)が電流の位相を 遅らせる働きがあるのがわかった。 |
これが工場で動力を使った場合、力率が悪くなる正体なのだ。RC直列回路 交流編
力率改善を行なうにはコンデンサーが使われると本に書いていた。 そこでコンデンサーを使った場合の位相のズレを見てみる事にした。 そのために、まずはRC直列回路を考える。
| RC直列回路 交流 |
|---|
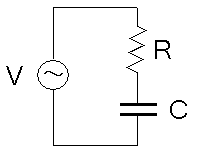 |
| 抵抗とコンデンサーが直列につながった回路だ。 |
さて、回路の中を流れる電圧と電流を計算する事にする。 ここでも、てっとり早い方法として、微積分を使って解く事にした。
| 各部分にかかる電圧を算出してみる |
|---|
 |
|
抵抗、コンデンサーにかかる電圧を求めてみる。 今度は三角関数の積分が出てきた。 一般的には、不定積分の場合、関数の積分結果だけでなく 任意定数も考慮する必要があるのだが、電圧も三角関数で 他の要素なんて考えられないので、任意定数は無視する |
そして抵抗、コンデンサー、それぞれの電位を足し合わせると この回路の電圧が算出できる。
| 回路の電圧計算の結果 |
|---|
 |
|
算出された電圧の変位が正弦波(サインカーブ)になる事がわかる。 すっきりした形にするため、三角関数の合成を行なった。 ここでも電圧と電流の波形で、α分の位相のズレが 生じるのがわかる。 |
先に、インピーダンスを求める。
| RC直列回路のインピーダンス |
|---|
 |
|
桃色で囲んだ部分はインピーダンスだ。 この時は気づかなかったが、角速度が大きくなれば インピーダンスは小さくなる。これを応用したのが ハイーパス回路なのだ。 |
さて、RC回路における位相のズレ「α」を見てみる。
| 位相のズレ「α」について |
|---|
 |
| 常に位相のズレ「α」が負の値を取る事がわかる。 |
そして電圧と電流の変位をグラフにしてみた。
| 電圧と電流の変位をグラフ |
|---|
 |
|
電圧の正弦波と電流の正弦波を比較すると 電流の正弦波が「α」分、進んでいる事のがわかる。 これにより、コンデンサーは電流の位相を 進ませる働きがあるのがわかった。 |
意図的に位相を進ませるために使うコンデンサーの事を 進相コンデンサー というのだ。 コンデンサーに、こんな役目があったとは知らなかった。RLC直列回路 交流編
コイル(モーター)は電流の位相を遅らせる働きがあり コンデンサーには電流の位相を進ませる働きがある事がわかった。 そこで、模擬的にコンデンサーを使ったモーターの力率改善を 考えてみる事にした。 ちょうど良いのがRLC直列回路なのだ。
| RLC直列回路 交流 |
|---|
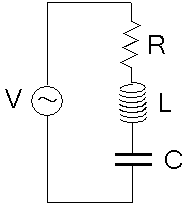 |
| 抵抗とコイル、コンデンサーが直列につながった回路だ。 |
さて、回路の中を流れる電圧と電流を計算する事にする。 ここでも、てっとり早い方法として、微積分を使って解く事にした。
| 各部分にかかる電圧を算出してみる |
|---|
 |
|
抵抗、コイル、コンデンサーにかかる電圧を求めてみる。 そして、個々の電圧を足し合わせたのが、回路全体の電圧だ。 |
そして三角関数の合成を使って、電圧の式をすっきりさせる。
| 回路の電圧計算の結果 |
|---|
 |
|
ここでも電圧と電流の波形で、α分の位相のズレが 生じるのがわかる。 |
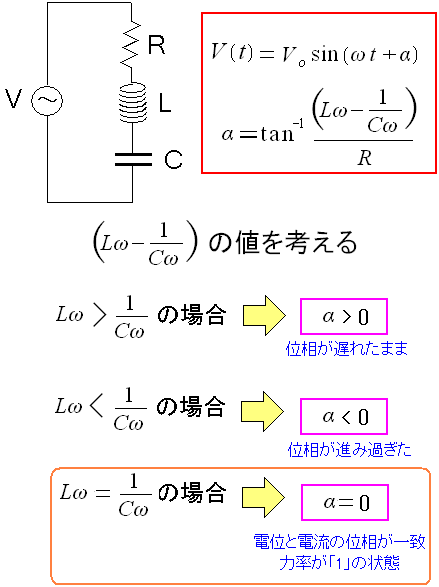
さて、RLC回路における位相のズレ「α」を見てみる。
| 位相のズレ「α」について |
|---|
 |
|
位相のズレは、コイルのインピーダンス、コンデンサーの電気容量 交流電流の角速度(周波数)に依存する事がわかる。 この微妙な調整で、力率改善を行なうのだ。 |
そしてインピーダンスを求める。
| RLC直列回路のインピーダンス |
|---|
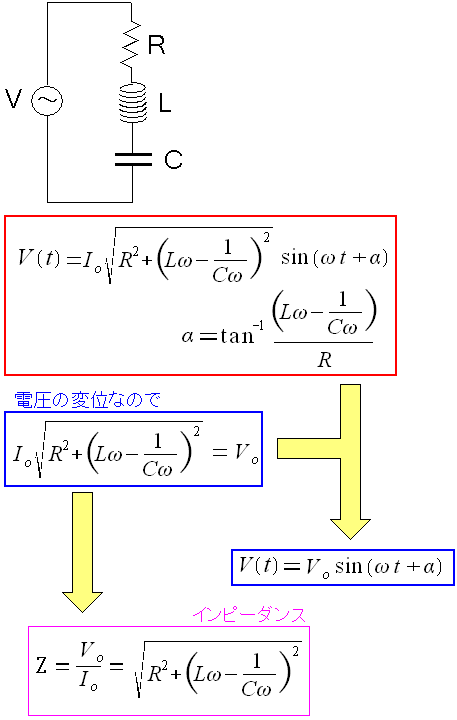 |
| 桃色で囲んだ部分はインピーダンス(電気の通しにくさ)だ。 |
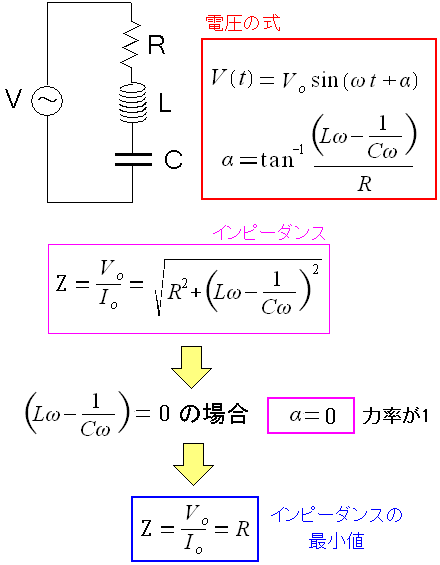
ここでインピーダンスに注目してみる。
| RLC回路のインピーダンスを考えてみる |
|---|
 |
|
力率が「1」の場合、即ち、電圧と電流の間に位相のズレがない場合 インピーダンスは最小値の「R」になる。 力率が「1」の場合、一番電気を通しやすい状態という意味なのだ。 |
力率が良ければ良いほど、回路内の電気を通しすい事を意味する。
なので
皮相電流を効率良く有効電流にできる
のだ。
ところで以下の回路の場合でも力率改善できるかどうか
確かめようとした。
| RL直列とコンデンサーとの並列回路 |
|---|
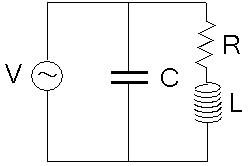 |
| RL直列部分をモーターと考え、並列してコンデンサーを置いてみた。 |
だが、この回路の場合 計算が複雑なため、途中で挫折したのだ (--;; それもそのはず。 三角関数と微積分を使って解こうとしたら単振動の数式などが出てきた。 学生時代なら「一応、理系の意地」で頑張ったかもしれないが 10数年ぶりの三角関数の前に討ち死になのだ だった。 理系だったのは過去の話。20世紀の話。 21世紀の今、未来志向の私は、過去を捨て、あっさりと挫折したのだ (^^)
交流から直流に変換する装置 AC-DCコンバーター
本を読み進めるとコンバーターの話が出てきた。 交流から直流に変換する装置だ。
| コンバーターの意味 |
|---|
|
コンバーター(converter)とは変換器の意味だ。 交流から直流に変換する装置の事をAC-DCコンバーターという。 ACは「Alternate current」の略で、交互に起こる流れ(交流)で DCは「Directory current」の略で、一直線の流れ(直流)だ |
電子機器にAC-DCコンバーターが必要な理由は・・・ 一般的な電子回路は直流でしか動かない のだ。 知らなかった (^^;; ついでに書くと AC-DCコンバーター装置の事を電源回路という も知らなかった。 電源装置には2種類あるという。
| 2種類の電源装置 | |
|---|---|
| リニア電源 | 昔から使われていた方式で 回路の構造が簡単だという。 その反面、大きな変圧器(トランス)が必要だったり 変圧器から熱が発生するため、直流変換時の 電気の無駄が大きい問題もあった。 |
| スイッチング電源 |
回路は複雑だが、小型化ができるだけでなく 無駄な電力も発生しない利点がある。 今の電子機器では、これが主流になっている。 |
2種類あるとは知らなかった。 まずはリニア電源の話を見ていくことにした。ダイオードと整流
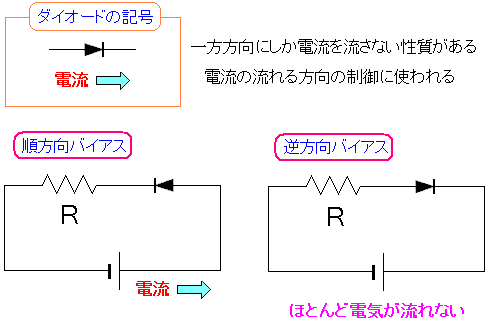
交流を直流にする際に必要になるのはダイオードだ。 ダイオードとは電流を一方方向のみ通す部品の事だ。
| ダイオードの働き |
|---|
 |
|
ダイオードは一方方向にしか電気を流さない。 その性質を利用して、電流の方向の制御に使われたりする。 電流の流れの向きにダイオードを設置した場合を順方向バイアスと呼び 反対方向の向きにダイオードを設置した場合を逆方向バイアスと呼ぶ。 (注意) 厳密にいうと逆方向バイアスであっても、僅かに電流は流れる上 大電圧がかかると、電気が流れる。でも、ここでは割愛します。 |
ダイオードの仕組みについては「システム奮闘記:その103」をご覧ください。 メモリの基礎 パソコンのメモリ入門 SRAM DRAM ダイオードを入れた交流回路を考える。
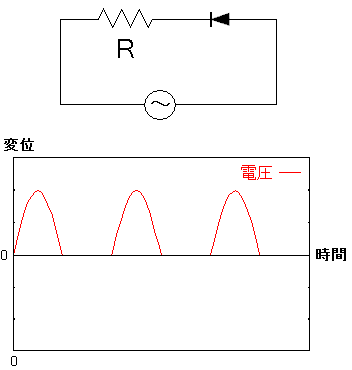
| ダイオードを入れた交流回路 |
|---|
 |
|
ダイオードは一方方向にしか電気を流さないため 交流電流の場合、片方の方向の部分だけしか流れなくなる。 このように片方だけ電気を流す回路を「整流回路」と呼ぶ。 (余談) この回路に抵抗をいれています。 ダイオードだけで入れると、大量の電気が流れて ダイオードが破壊される可能性があるため 電流制御のために抵抗を入れるのが一般的なのだ。 それに習って、意図的に抵抗を入れています。 |
ダイオードを1個使った場合だと、交流電流のうち 片方向の電流のみ取り出す事ができた。 だが、これでは半分の電気を無駄にしている。 そこで4つのダイオードを組み合わせたブジッリ整流回路が使われる。
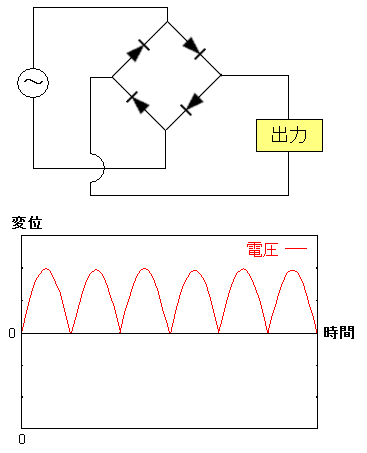
| ブジッリ整流回路 |
|---|
 |
|
ブリッジ整流回路を使うと交流電流の成分を全て同じ方向に 変換できるため、無駄がなくなる。 4つのダイオードを組むだけで同じ方向に向くのだから 仕組みとしては簡単だ。 |
でも、このままだと波打った状態なので、電圧を一定にさせる必要がある。 そこで使われるのがコンデンサーだ。
| ブリッジ整流回路にコンデンサーを組み込む |
|---|
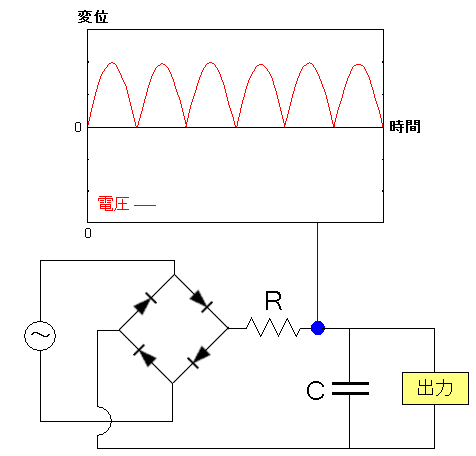 |
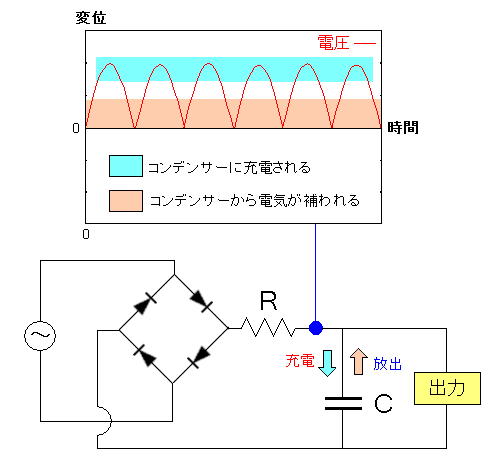
コンデンサーを組み込む事で何が起こるのか見てみる。
| コンデンサーを組み込む事で起こる事 |
|---|
 |
|
コンデンサーの手前では整流回路で同じ向きになった波形だ。 コンデンサーには充電の役目がある。 波形の山の上側(余分な電圧)の時、コンデンサーに充電される。 電圧が下がり、波形の谷の部分になると、コンデンサーに 溜められた電気が放出される仕組みになる。 |
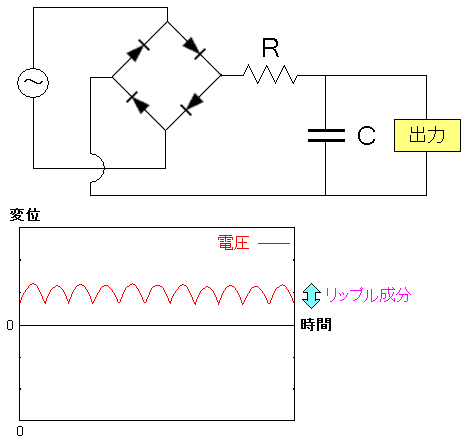
コンデンサーの充電機能を使った結果、波形が以下のように変化する。
| コンデンサーの充電機能を使った結果 |
|---|
 |
|
コンデンサーを使う事で、波形の振幅が小さくなる。 だが、まだ波形が残っている。この残った波形をリップルと呼ぶ。 リップル(ripple)とは「さざ波」や「波形」の意味だ。 日本語を使えと思いたくなる・・・。 リップル除去のためには、もう1つコンデンサーを使って より平らに近づけたり、ツェナーダイオードを使ったりする。 (補足) コンデンサーの手前に抵抗器をつけている。 それはコンデンサーに充電された電気が放出される際 整流器の方に流れ、ダイオードを破損するのを防ぐためなのだ。 それと余分な電圧(リップル)を除去する役目もある。 |
定電圧ダイオード(ツェナーダイオード)
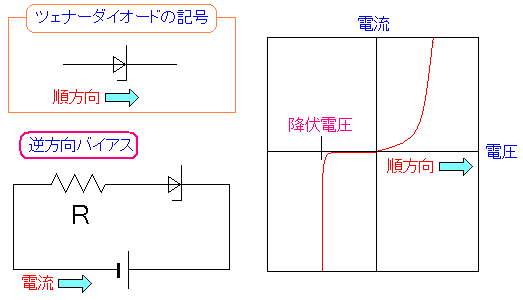
さて、リップル除去の話が出てきたので、リップル除去に使われる 定電圧ダイオード(ツェナーダイオード)の話を触れたいと思います。 ダイオードには順方向にしか電気を流さない性質があると書いたのだが 逆方向でも、ある一定の電圧になると、電流が流れる性質がある。 それが定電圧ダイオードというものだ。
| 定電圧ダイオード(ツェナーダイオード)とは |
|---|
 |
|
普通のダイオードと同じ特性を持つ。 だが、逆方向にある一定以上の電圧をかけると 電流が無断大に流れるようになる。 この現象の事をツェナー降伏と呼ぶ。 この現象が起こる電圧を降伏電圧という。 |
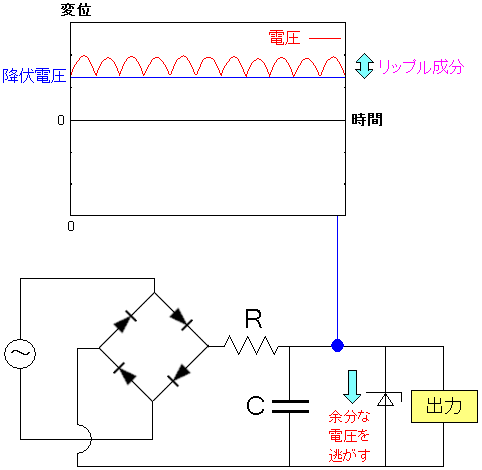
ツェナーダイオードの性質を利用して、先ほどの ブリッジ整流回路に組み込むと以下のようになる。
| ブリッジ整流回路にツェナーダイオードを組み込む |
|---|
 |
|
リップル成分を含んだ電気が流れてくる。 降伏電圧が、リップル成分よりも少し低い電圧の ツェナーダイオードを用意しておく。 |
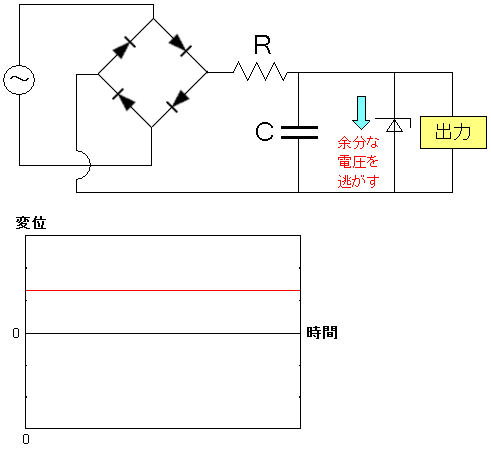
すると、以下のようになる。
| 波形が平らになった |
|---|
 |
|
ツェナーダイオードにより余分な電圧部分を逃す事で 波のない平らな直流電流ができるのだ。 |
ところでツェナー降伏が起こる理由なのだが
それは割愛します。そのわけは
トンネル効果を説明しないといけないのらー!
量子力学の世界になる。
江崎玲於奈博士がノーベル賞を受賞したトンネル効果の話になるのだ。
| 「トンネル効果」を例え話で説明してみると |
|---|
|
刑務所の塀の中の囚人が、ジャンプしても乗り越えられないはずの 高い塀を、乗り越えてシャバへ出るという離れ技を行なう現象なのだ。 まるで塀にトンネルがあるかの如く、塀をすり抜ける感じなので トンネル効果と呼ばれる。 顕微鏡でも見えない原子の世界では、日常では考えられない現象が 起こっているのだ。 |
私が説明できるのは、この程度なのだ (^^)
「もっとしっかり説明せんかい!」の声があるかもしれませんが
堂々と反論します。
ただでさえ、電磁気でも息切れなのに、量子力学を勉強しても・・・
確実、打ち死になのらー! (--;;
私が理系だったのは20世紀の話。遠い過去。
21世紀の、今、未来志向の私は、あっさりと諦めるのだ (^^)
| アバランシェ降伏について |
|---|
|
ダイオードに、逆方向に大電圧をかけると、ツェナー降伏とは別に 無限大に電流が流れるようになる現象がある。 アバランシェ降伏という現象だ。 ただ、ツェナー降伏の原理「トンネル効果」とは異なり ダイオード内の半導体で起こる雪崩現象(カスケード現象)なのだ。 もちろん、アバランシェ降伏の話も割愛します。 |
交流から直流へ変換する話を簡単に書きました。 ここで紹介した方法はリニア電源の仕組みだ。 でも、今や主流はスイッチング電源になっているのだ。スイッチング電源
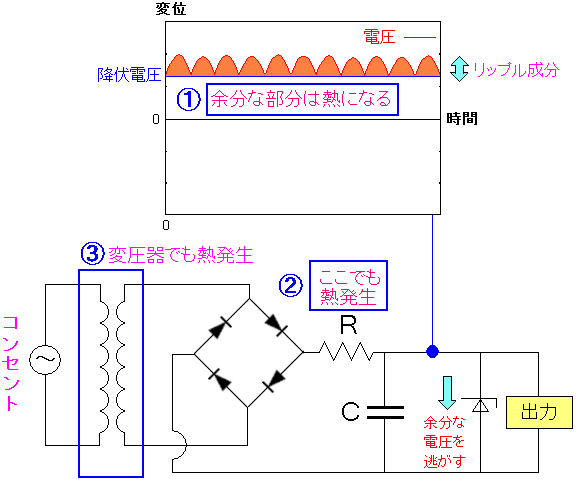
リニア電源の仕組みを説明したのだが、 リニア電源の場合、装置が大きくなるだけでなく 電力の無駄使いが起こっている。
| リニア電源の問題点 |
|---|
 |
|
コンセントから変圧器で電圧を下げる際、ここで熱が発生している。 そして抵抗器でも熱が発生する上、リップル除去分も熱になっている。 使い道のない熱になってしまうため、非常にもったいないのだ。 |
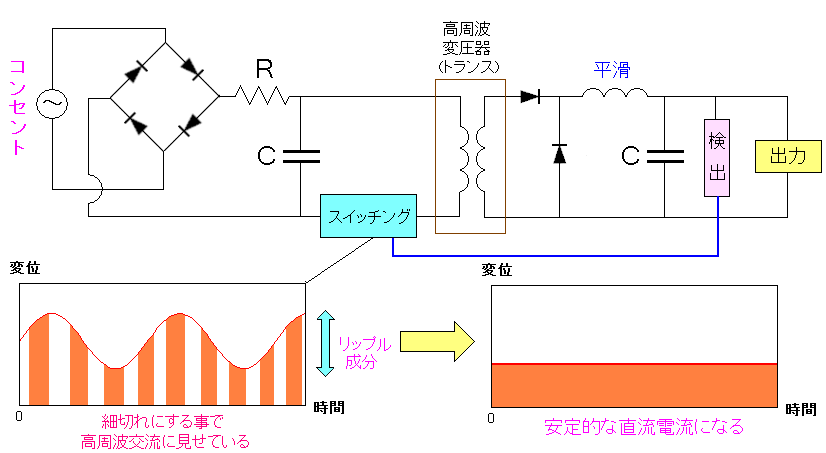
今では、電力の無駄が少ない変換方法のスイッチング電源が主流だ。 その仕組みを見てみた。
| スイッチング電源の仕組み |
|---|
 |
|
コンセントから取り込んだ交流電流は、すぐに整流器で直流化される。 そしてスイッチングで高周波パルス波(交流)に加工して 高周波用変圧器で電圧を変更する。 そして整流を行なって、直流化する仕組みだ。 スイッチング装置で高周波パルスにするのは 変圧器のコイルの巻き数が少なくて、十分な磁場が発生し 相手側のコイルで発生させるだけの十分な起電力を生むからだ。 |
直流を作るのに、直流化した後、交流化して、直流にする。 複雑な方法なのだが、これが電力の無駄がない方法だという。
インバーター 直流から交流に変換する装置
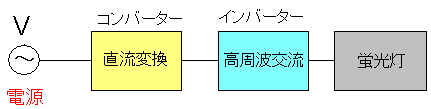
AC-DCコンバーターは交流から直流に変換する装置だった。 反対に、直流を交流に変換する装置としてインバーターがある。 本にはインバーター付蛍光灯の話があったので読んでみる事にした。 驚いた事に・・・ 交流を直流にした後で、交流にしている!! インバーター付蛍光灯の概略を描けば、次のようになる。
| インバーター付蛍光灯の概略 |
|---|
 |
|
交流電源から取得した電気を直流に変換した後で 高周波数の交流に変換して蛍光灯を照らす仕組みだ。 高周波交流なのでチラつきが人間の目にはわからない上 50Hz/60Hz地域関係なく使えるのだ。 |
もう1つのインバーター付蛍光灯の利点は 従来のグロー点灯管式よりも明るい! のだ。 蛍光灯の中に、高周波交流を送り込んでいるため 水銀原子と電子の衝突の数が増え、同じ電力だと、明るくなっているのだ。 もし、従来のグロー点灯式と同じ明るさで良ければ 少ない電力で済むため 消費電力を抑えられる のだ。 問題点もあり、高周波装置から出るノイズがあるため ノイズ除去などを行なう必要があるのだ。 ところで、この時、高周波交流を作るのに、一度、直流にして、 その後で、高周波交流にする理由は、わからなかった。電車のモーター 交流モーターとインバーターについて
交流から直流の話を書いている時に、ふと思いついた事がある。 新幹線のモーターだった。 新幹線の架線には2万ボルトの交流が流れている。 だが、0系、100系は直流モーターを使っていた。
| 新幹線の0系、100系について |
|---|
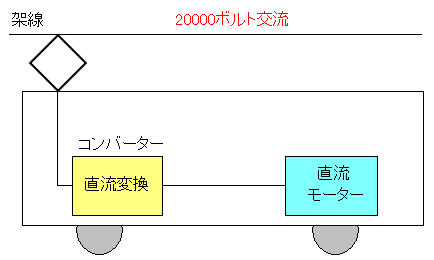 |
|
新幹線の0系、100系は架線の交流電流を取り込んで 直流化し、直流モーターを回していた。 床下で交流から直流に変換していたのだ。 |
1992年に登場した「のぞみ」の車両(300系)では交流モーターになった。
| 新幹線300系の車両 |
|---|
 |
|
300系の車両から交流モーターが使われるようになった。 それを知ったのは数年前の話なのだ。 |
数年前に新幹線のモーターが交流モーターだと知ったのだが
その先は調べる事はしなかった。そのため
架線から取得した交流電流をそのまま使える車両だと思い込んだ。
| 300系以降の新幹線の仕組みを 以下のように誤解していた |
|---|
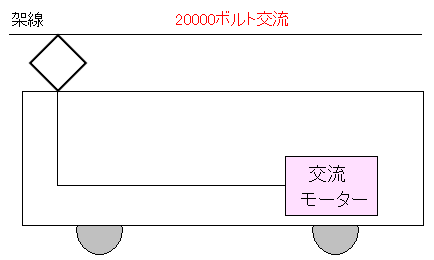 |
|
300系の「のぞみ」車両以降、交流モーターを使っている事から 架線の交流電流を電圧を変えてモーターを回していたと思っていた。 |
だが、その誤解を解くキッカケがあった。 それは、2012年になって知った衝撃な事だった。 阪急電車の架線は直流なのだが・・・ 阪急電車の新しい車両のモーターは 交流モーターが使われている!!
| 阪急電車8000系車両(御影駅) |
|---|
 |
|
阪急電車の車両で、2200系で試験的に交流モーターが使われ 8000系から本格導入している。 そういえば、8000系が登場した時、発車の際に 他の車両とは異なる音が聞こえると思っていた。 それが何なのか気にしなかった。 それがインバーターの音だと知ったのは 20年もたった2012年なのだ (^^;; |
だが、新幹線と違い、阪急電車の架線は1500ボルトの直流だ。
なぜ、わざわざ交流モーターを使っているのか
理由が全くわからへん・・・
だった。
阪急電車の8000系以降は、こんな風になっているのだ。
| 阪急電車の8000系以降の車両 |
|---|
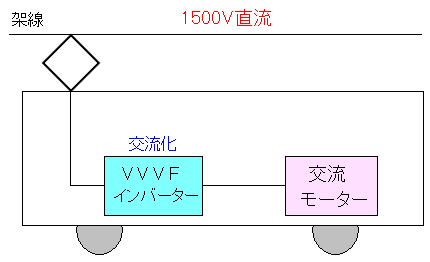 |
|
直流電流をインバーターを使って交流化して 交流モーターを回しているのだ。 電車に搭載されるインバーターは「可変電圧可変周波数制御」ができ 英語にすると「Variable Voltage Variable Frequency」の事から VVVFインバーターと呼ばれているのだ。 |
そこで実際に阪急電車の車両の床下をのぞいてみる事にした。 9000系のVVVFインバーターを見つける事ができた (^^)
| 阪急電車9000系のVVVFインバーター |
|---|
 |
| 車両が新しいため、表示が綺麗に撮影できた。 |
ふと思い出した。 以前、近鉄に乗った時、インバーターの文字があったので 何を意味するのか、わからなかったが、とりあえず撮影した写真が ある事を思い出した。 探してみたら、あったのだ。
| 近鉄の車両 |
|---|
 |
|
近鉄の車両にインバーター(INVERTER)の文字があった。 この車両が交流モーターを使って動かしているのがわかる。 でも、どうして、わざわざインバーターの文字をいれているのか 鉄道マニア向けなのか、車両整備の際に、わかりやすくしているのか。 |
ところで、架線の電気は直流なのに、わざわざ交流モーターを 使う事になったのか、その理由を調べてみる事にした。
| 交流モーターを採用する理由 | |
|---|---|
| (1) | 直流モーターの場合、整流子モーターを使うため ブラシが擦り減ったりするため、 モーターの保守・点検が必要だった。 交流モーターの場合、誘導モーターを使っているため ブラシが不要で、保守・点検の手間が省けるため |
| (2) |
交流の誘導モーターを使うと、周波数でモーターの回転数を 制御できるため、回転制御がしやすい。 |
交流モーターを使う理由は
電力の無駄を大幅削減!
なのだ。
その理由は以下の通りだという。
| 直流モーターを使った場合(抵抗制御方式) |
|---|
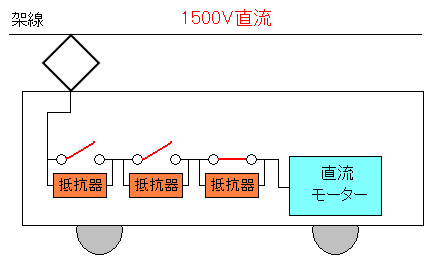 |
|
直流モーターの制御を行なう場合、抵抗を使っている。 抵抗を多く使えば、電圧が下がるという仕組みだ。 だが、これだと低速運転(回路が抵抗器につながっている)場合 電力が抵抗器によって熱エネルギーとして消費されるため 電力の無駄使いになっている。 |
抵抗制御方式を使っている阪急5000系を見てみた。
| 阪急電車の5000系の車両の抵抗器 |
|---|
 |
| 茶色で囲んだ部分が抵抗器になる。 |
だが、これでは無駄使いが多いという事で、直流モーター車両で 改良されたのが、チョッパ制御方式だ。
| 直流モーターを使ったチョッパ制御方式 |
|---|
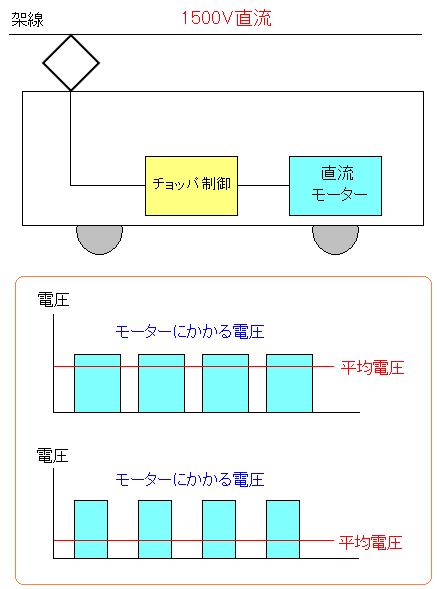 |
|
直流モーターの制御をチョッパ制御器を使う これだと抵抗器を使わないで制御するため節電ができる。 基本的な原理は、単に電源を入れたり、切ったりするだけなのだ。 (ウソのようなホントの話) |
そこで、今度は阪急の7000系車両の床下を撮影する事にした。
| 阪急電車7000系のチョッパ器 |
|---|
 |
|
阪急の7000系の場合、界磁チョッパ器を使っている。 人間の目では「界磁チョッパ器」の表示が見えたのだが 安物のデジカメで撮影したため、写真には綺麗に写らなかった。 |
だが、交流モーターとVVVFインバーターの登場によって
直流モーター自体を使わなくなったのだ。
ところで長年、直流モーターが使われてきた。
その理由は、交流の場合、制御に問題があった。
そのため、直流モーターを使う方が安上がりだった。
だが時代は進化する。
交流モーター登場の理由は・・・
パワーエレクトロニクスの進化
なのだ。
安価で交流化や、電圧・周波数の制御装置ができるようになったため
交流誘導モーターの導入が可能になったからだ。
| 映画「阪急電車」の車両は3000系 |
|---|
 |
|
映画「阪急電車」で使われた3000系の車両。 VVVFインバーターどころか、チョッパ器すらない 昔の車両なのだが、阪急らしい車両がする。 もし、VVVFインバーターがついた9000系を走らせたら 撮影用に走らせた臨時列車の電気代は、どれくらい節約できるのか 興味を持ってしまった。 だが、主に3000系(時々、5000系と7000系)が走る路線のため インバーター付の新しい車両が今津線を走ると違和感があるのだ。 |
ところで、新幹線の電気系統を調べたら、衝撃的な事を知った。
取得した交流電流を直流化して、交流化している!!
だった。
つまりこんな感じなのだ。
| 300系以降の新幹線の車両について |
|---|
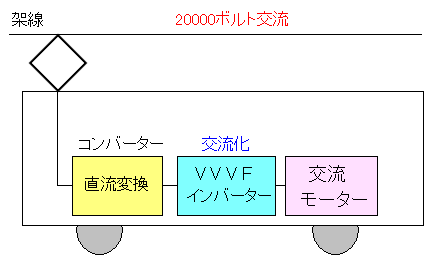 |
|
架線から取得した交流電流を直流化している。 そしてVVVFインバーターで交流化しているのだ。 |
なんで、こんなややこしい事、するねん! と思った。 調べてみる事にした。 交流の周波数は直接は変更できへん! のようだ。 そのため、一度、直流にした後で、交流化しているのだ。 ふと気づいた。 西日本と東日本では周波数が違うから電力の融通が困難だ。 2011年3月11日の大震災の時、電力の融通が困難な事が問題になった。
| 周波数変換所は3ヶ所ある |
|---|
|
西日本は60Hzの交流。東日本は50Hzの交流を使っている。 そのままでは電力の融通ができないため、変換を行なう必要がある。 現在、日本に3ヶ所ある。合計で100万Kw変換能力がある。 でも、大災害でどちらかが電力が不足した場合、100万KWでは足らない。 周波数の統一をするのが国の安全保障につながるのだが 政府や電力会社は、まるでやる気がないのが現状だ。 もちろん、既に導入済みの電化製品の問題などもあるため 容易な話ではなさそうなのだが。 |
阪急電車と新幹線の話題になっていたので、ここで、ちょっと余談。 阪急電車と新幹線との関連性を紹介します。
| 新幹線の線路を最初に走った営業列車は阪急電車 |
|---|
|
阪急電車と新幹線の共通点は線路の幅が同じ標準軌だ。 そのため新幹線の線路の上を阪急電車が走ったという 衝撃の事実があるのだ。 阪急電車の上牧から大山崎までの区間、地平を走っていた。 天王山と淀川に挟まれた狭い場所のため、新幹線の建設の際 国鉄は用地確保ができずに困っていた。 そこで阪急の線路の上を高架にして、地面を阪急、 高架を新幹線を走らせる事を考えた。 だが、新幹線を高架にすれば、その高架の重みで 阪急の線路が地盤沈下のおそれがあった。 そこで阪急の線路の隣に新幹線の高架という事になったが 高架によって、阪急の運転手にとって見通しが悪くなり 高架の所にある踏み切りでの事故などが指摘され 安全のため阪急は高架を迫られた。 阪急の営業を止める事なく、阪急の高架を実現するために できた新幹線の高架を上を、一時的に、新幹線の線路を走らせ その間に阪急の高架工事を行なったのだ。 鉄道ファンの間でなくても、関西で知っている人は結構いる話だ。 鉄道トリビア 新幹線の線路を走っている阪急電車の写真(昭和38年:1963年) 東海道新幹線・阪急京都線 youtubeにある阪急電車が新幹線の線路の上を走っている動画 阪急電車と新幹線 あまり知られていない真実 |
電車と電気回路 (2016年5月追加) ふと思った。 架線で電気を供給するが 戻りの電気はどうするねん? 電気の場合、行きと帰りの線がある。 (3相交流は別だが・・・) 鉄道の話は好きなので、電気の帰り線は線路なのは知っていた。 でも、念のためネットで調べてみると資料を発見。 車両から変電所までの電気の流れ(鉄道総合技術研究所:PDF) やっぱり線路なのだ!!
| 電車の送電と戻り線 |
|---|
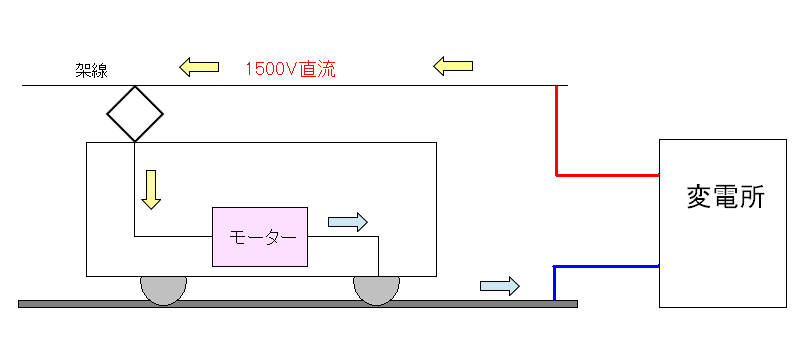 |
|
変電所から架線を伝って、電気が電車に供給される。 戻りの電気は、線路を伝って変電所に戻るのだ。 |
線路と線路の間の繋ぎ目にはレールボンドと呼ばれる物がある。 線路と線路を結ぶ電線だ。
| レールボンド(阪急電車:西宮北口駅付近) |
|---|
 |
|
線路の繋ぎ目にある電線が、電気を流すための物だったのは知らなかった。 (西宮北口について) 西宮北口といえば、昔、阪急ブレーブスの本拠地だった西宮球場があった。 だが、オリックスに売ってしまい、かつての球場は取り壊され 今では商業施設「西宮ガーデンズ」になっている。 |
ところで阪急電車のように直流で動く電車の場合、戻り線から 地面に電気が漏れ出す現象が起こるという。
| 線路から電流が地面に漏れ出す現象 |
|---|
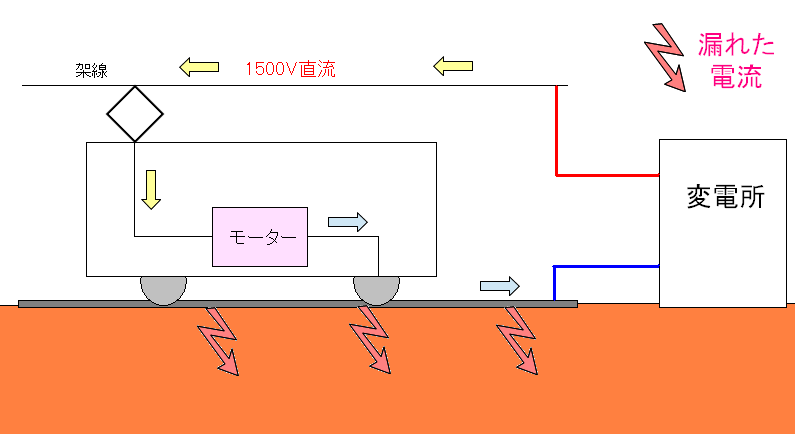 |
|
直流の場合、電流が地面に漏れ出す事で問題を引き起こす。 交流の場合も、電流が地面に漏れ出しているが、直流ほど問題ではないようだ。 |
その現象とは
電食
なのだ。
電食のはなし(公益社団法人 日本電気技術者協会)
電食(鉄道総合技術研究所:PDF)
線路や、線路の下に埋まっている金属でできた配管が、漏れ出した電流によって、
電気分解と同じ現象を起こり、腐食を引き起こすのだ。
ガス管だとガス漏れの恐れがあるし、水道管だと水漏れの恐れがある。
そのため線路の地下には、漏れ出した電流を吸い取る電線を引いていたりするという。
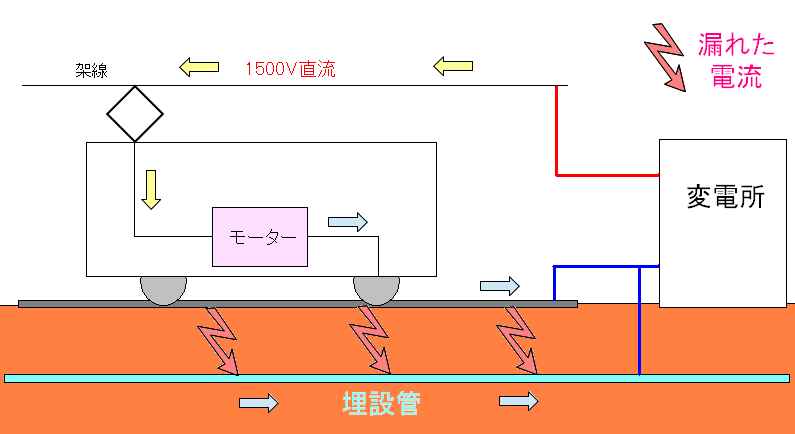
| 線路の下に埋設管の設置 |
|---|
 |
|
線路の下に金属の管を埋め込み、漏れ出した電流を吸い取り 変電所まで送り返す役目を果たしている。 |
そんなこと・・・ 全く知らへんかった!! でも、これで少しは鉄道好きの嗜みを身につけたのだ。インバーター付エアコン
インバーター付エアコン。節電効果があるといわれる。 これも電車の交流モーター同様、電圧と周波数の制御が しやすくなったからだ。 現代荷電の基礎用語 インバーターエアコンとは 少しでも技術の話を知ると、世の中の進歩を感じる事ができる。
電気と安全について
家庭用電気は100Vなのだが、触れれば、感電する危険がある。 他にも電気については、気を付けないといけない事がある。 そこで電気回路を通じて勉強になった事を載せたいと思います。雷サージ対策
電気回路の本を読んでいて雷サージが出てきた。 一体、何やねん! そこで本を読んでみると、以下の現象が起こるのを知った。
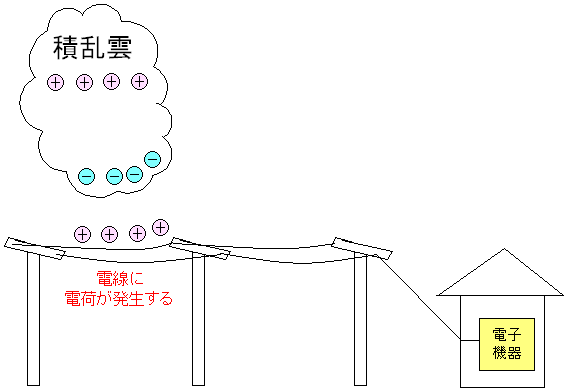
| 雷サージが起こる状態 |
|---|
 |
|
積乱雲が発生して、雲の上ではプラスの電荷、雲の下には マイナスの電荷が帯電する。その影響で電線や電話線などに プラスの電荷が帯電する現象が起こる。 |
そして雷が鳴り、積乱雲の中に帯電していた電荷がなくなると 電線や電話線に溜った電荷の行き場がなくなる。
| 雷サージが起こる状態 |
|---|
 |
|
行き場を失った電荷が各地に押し寄せ、コンセントを通じて 家庭にある電子機器を直撃し、電子機器に損傷を与えるのだ。 |
こんな話、知らへんかった
そのための対策として定電圧ダイオード(ツェナーダイオード)が
使われるのだ。
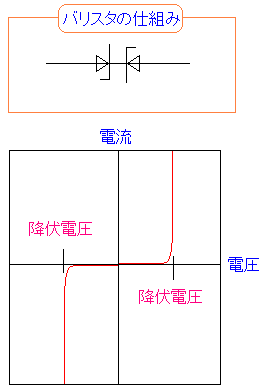
| バリスタの仕組み |
|---|
 |
|
定電圧ダイオード(ツェナーダイオード)を2つ組み合わせて 作った物をバリスタという。 定電圧ダイオード(ツェナーダイオード)の性質で ある一定以上の電圧がかかると 電気が流れる仕組みを応用した物だ。 |
バリスタを使った電子機器が以下のような物だ。
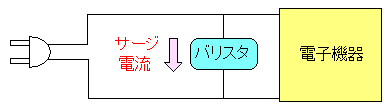
| バリスタを組み込んだ電子機器の仕組み |
|---|
 |
|
コンセントの所から電子回路までの間にバリスタを入れておく。 そしてコンセントを通じて、高圧電流が流れてきても 上手に逃す形になるのだ。 |
初めて知った。
そこで雷サージに関して検索したりしていると
電源タップでも雷サージ対策の物がある!!
これも初めて知った。
そして会社の電源タップを見てみると、一部のタップだが
雷サージ対策の電源タップがあった。
| 雷サージ対策付の電源タップ |
|---|
 |
|
会社で使っている電源タップで、雷サージ対策付のものだ。 こんな表記があったとは、気づかなかった。 |
あとは電話回線でも雷サージは起こる。
| LANボードと雷サージ |
|---|
|
電話回線でも雷サージは起こるため、電話線を使って 大量の荷電が家庭のパソコンのLANケーブルに 押し寄せる場合もあるというのだ。 この場合、LANボードが損傷する事があるため LANの方も注意が必要というのだ。 |
落雷による瞬電について
雷サージの話が出てきたので、少し瞬電について触れたいと思います。 落雷時に瞬間的に停電が起こる事があります。 蛍光灯が消えたりする事がありますし、その時にパソコンの 電源が切れてしまう事があったりします。 なぜ瞬間的に停電が起こるのか 全く知らへんかった (^^;; なのだ。 そこでUPSを購入する前に、瞬電について調べてみる事にした。 関西電力 雷が電気に与える影響 雷が電線に高圧電線などに直撃した場合、大量に電気が流れるのを 防ぐために、送電回路を遮断して、別回線に切り替えるため 0.7〜2秒の間、停電が起こるというのだ。 これは電力会社がやっている安全対策なのだ。コンセントの極性
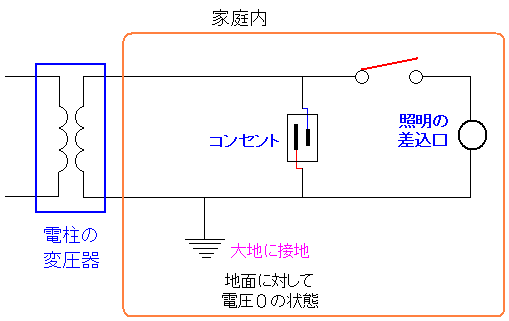
本にコンセントの極性があった。 それを知った瞬間・・・ マジかよ?! どないして区別するねん! と思った。 コンセントの差し込み口で、2つの穴の長さが違うというのだ。 そこで見てみると・・・ ホンマに長さが違うやん!
| コンセントの差し込み口 |
|---|
 |
|
左側の方の穴の方が長くなっている。 長い穴の方を触っても感電しないのだ。 |
どういう事か見てみると家庭内の電気配線は 以下のようになっているというのだ。
| 家庭内の電気配線 |
|---|
 |
|
家庭内の配線で、片方が地面に設置しているため 地面との電圧の差がない(電圧0ボルト)なのだ。 コンセントの差し込み口の長い方は、電圧0ボルトにつながっている。 照明器具の差し込み口も電圧0V側についている。 スイッチを切っている間は触っても感電しない仕組みだ。 |
こんな安全対策があったとは知らへんかった! もちろん、いかなる時も、コンセントの差し込み口を触ったり 照明器具の差し込み口を触らない方が良いに決まっているが もしものための安全対策になっているのだ。 なので照明器具の交換の場合は、感電しないように スイッチを切って、交換を行なうべきなのだ。
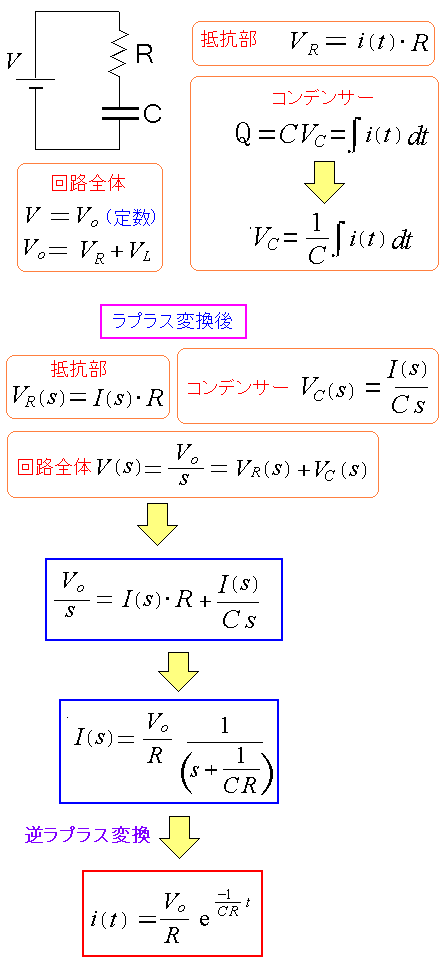
ラプラス変換
回路の問題を解く際にラプラス変換が使われるという。 ラプラス変換って何やねん? だった。 そこで調べてみる事にした。 ラプラス変換の定義式を見た。
| ラプラス変換の定義式 |
|---|
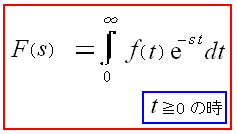 |
| tの関数を、Sの関数に変換する際の変換方法なのだ。 |
これを見た瞬間・・・
だから何をする関数なんや!
そこでラプラス変換の事を調べると以下のサイトを発見。
日本電気技術者協会 ラプラス変換とその使い方1<基礎編> ラプラス変換とは何か
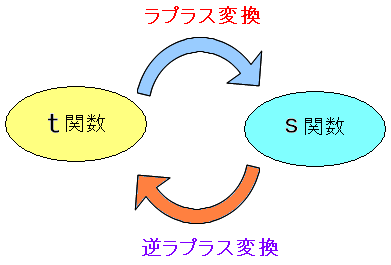
そして逆ラプラス変換を知った。
| ラプラス変換と逆ラプラス変換 |
|---|
 |
|
逆ラプラス変換とは、ラプラス変換でS関数にした物を 元の関数に戻すために行なう変換だ。 |
でも、これだけでは・・・
一体、何をする関数か、わからへん!!
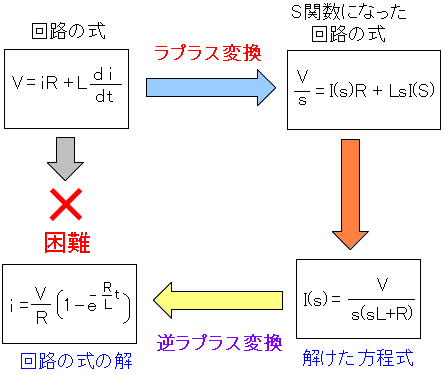
だが、サイトをじっくりみていくと、ラプラス変換の目的がわかったのだ。
| ラプラス変換を行なう目的 |
|---|
 |
|
回路の式などで微分方程式を含んだりする事がある。 直接、方程式を解く事が困難な場合、ラプラス変換を行なう事で 解きやすい方程式の形にして、方程式が解けた後 逆ラプラス変換を行ない、求めたかった方程式の解にたどり着く |
要するに・・・
解くのが困難な方程式を解くための手法
なのだ。
定義式を覚えなくても、ラプラス変換表さえあれば、道具として使える。
| 2016年5月に追加 | |||||||||
これだけの説明だったら、まだラプラス変換の目的がわからない。
そこで改めて調べ直してみた。
すると・・・
微分方程式を解くための手法
なのだ。
直流RL直列回路を解法を例にしてみる。
ラプラス変換は、時間関数の微分方程式に使われている。 時間関数からラプラス関数への変換表もあるので、これを使って、当てはめるだけで良いのだ。
直流RL直列回路の微分方程式の解法は以下のようになる。
非常に楽なのだ。 |
ラプラス変換で直流・RL直列回路を解く
交流ではなく直流のRL直列回路を解いてみた。
| 直流のRL直列回路 |
|---|
 |
|
求めたいのは電流の関数。 まずは抵抗、コイルにかかる電圧の時間関数を求め ラプラス変換でS関数に置き換える。 すると電流のS関数が簡単な四則演算で求まった。 三角関数も微分積分も使わない。 |
あとは逆ラプラス変換を使えば、電流の時間の関数が出てくるが 逆ラプラス変換したくても、変換表にはない。 だが、少し細工すれば、簡単な形に帰着できる場合が多いという。
| 少し細工 |
|---|
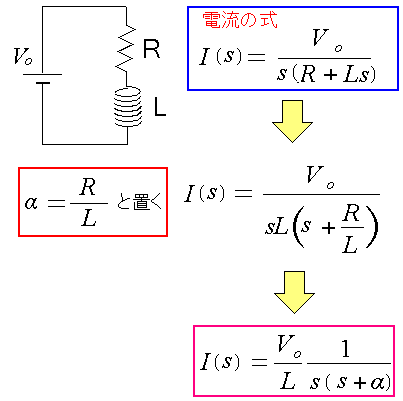 |
| 式を少し細工する。 |
細工する理由なのだが・・・ 部分分数分解法を行なうため なのだ。 名称は記憶にあるのだが・・・ どういう事なのか、忘れてもうた (^^;; そこで思い出しながら部分分数分解法を行なう事にした。
| 部分分数分解法 |
|---|
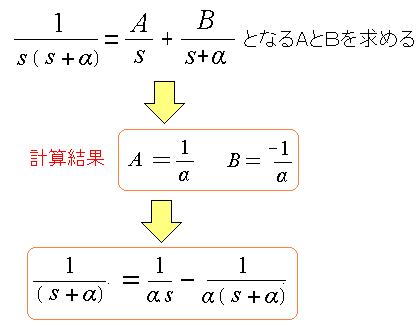 |
|
分数の積を、分数の和に変換する事なのだ。 これを行なう事で、逆ラプラス変換をしやすくするのだ。 |
そして、できた部分分数を使ってみる。
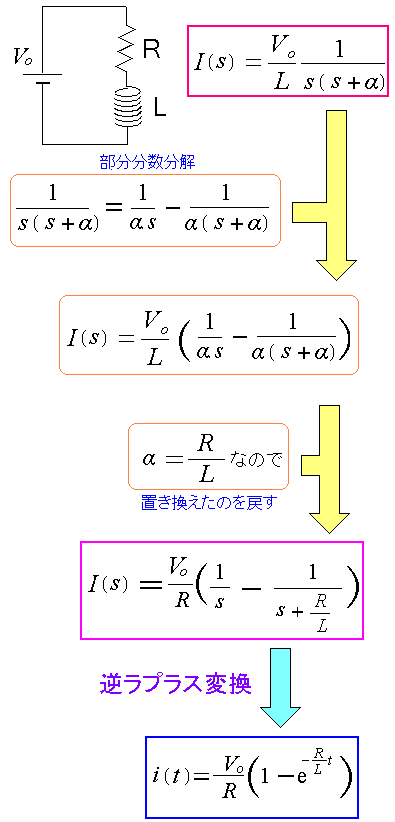
| 部分分数分解法を適用してみる |
|---|
 |
|
部分分数分解法で、上手に逆ラプラス変換にもっていけるようになった。 そのおかげで、簡単に電流の時間の関数が求まった。 |
ところで直流なので電圧が一定なら電流も一定のはずなのに どうして電流の式に第2項の関数式が出てくるのか。 この正体を図で説明すると、以下のようになる。
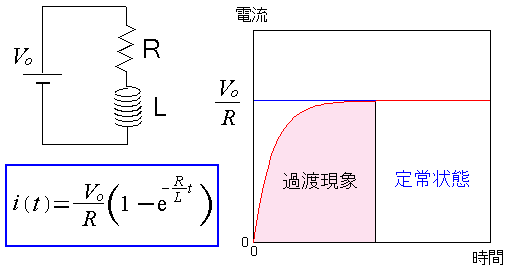
| RL回路の過渡現象 |
|---|
 |
|
電源を入れた場合、コイルの中の電圧が変化するため それに伴い、コイルが発生する磁場も変化する。 この時、磁場の変化を抑えようとする働きとして 誘導起電力が発生して、電流の流れが抑えられる。 交流のRL直列回路で、電流の位相が電圧の位相が遅れる話をしたが ここでも電圧が上がったからといって すぐに電流が増えるわけではないのだ。 この状態を過渡状態という。 そして電流の値が一定の値になった時、定常状態という。 |
今回の計算で、ラプラス変換を使って求める最大の利点がわかった。 過渡状態が見える! 事なのだ (^^)直流のRC直列回路
直流電源でのRC直列回路を考えてみる。 一般的にはコンデンサーは直流電流は流れないので こんな計算は無駄に思えたりするのだが、やってみる事にした。
| 直流のRC直列回路 |
|---|
 |
|
時間の関数のままだと微分方程式になるのだが ラプラス変換で、S関数にすると簡単な計算にできる。 そして計算結果が、逆ラプラス変換が行いやすい結果になったため そのまま逆ラプラス変換を行なった。 |
コンデンサーは直流を流さないのに
計算結果では電流が流れている!
なのだ。
どういう事なのか図にすると、以下の事なのだ。
| RC直列回路の過渡状態 |
|---|
 |
|
コンデンサーは直流電流は流さない性質があるのだが 電源を入れてから、コンデンサーに電気が充電されるまでの間は 充電のために電流が流れているのだ。この期間を過渡状態と呼ぶ。 |
コンデンサーに充電される様子まで見える!! ラプラス変換を使った解法だと、微積分で見えなかった 過渡状態までが見れるので、ラプラス変換の凄さに驚いた。 学生時代に、電気回路とラプラス変換に出会っていたら、 回路に興味を持って、電気・電子工学の技術者になっていたかもしれない。 もし、そうなっていたら、今頃はアンドロイドを使った 制御関係でオープンソースカンファレンスに出展していたかもしれない。ラプラス変換について考える
ラプラス変換は、解くのが困難な微分方程式を 解きやすくする方法だというのは、わかった。 では、一体、どういう数学的意味があるのだろうか。 少し興味があったので、調べようと思った。 以下の説明をしているサイトを発見した。
| ラプラス変換とは何なのか |
|---|
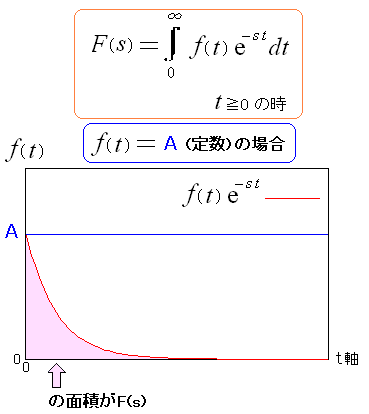 |
|
ラプラス変換する前の状態を定数「A」とする。 それをラプラス変換した時の関数が、色で塗った面積だという。 |
だから何やねん!!
面積だとわかっても、それが何を意味しているのか
全くわからない。
ラプラス変換する前の関数を、他の2つの関数で見てみる事にした。
| ラプラス変換 |
|---|
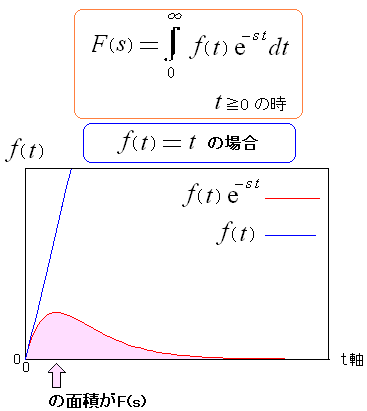 |
|
どうやら変数tの値が増加すればするほど 0に収束する関数にしているようだ。 |
そして、もう1つの関数で見てみる
| ラプラス変換 |
|---|
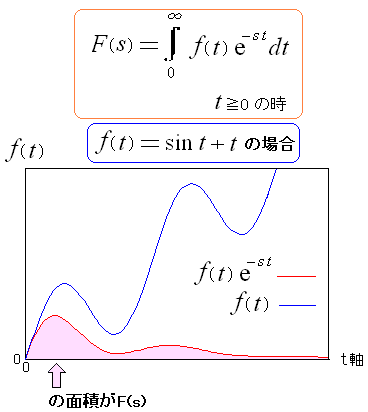 |
|
変数tを増加させると、0に収束させる関数になっている。 これだと面積の値は無限大になる事はなく、求められる。 |
この時は、ここで挫折したが、実は良い線だったのが 2016年になってわかったのだ。 ところでラプラス変換の定義式を、もう一度、見てみる。
| ラプラス変換の定義式 |
|---|
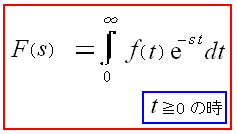 |
| 時間関数を、Sの関数(ラプラス関数)に変換する際の変換方法なのだ。 |
この式は・・・
フーリエ変換そっくり
なのだ。
ラプラス変換とは、フーリエ変換を細工した物なのだ。
フーリエ変換とは、任意の関数を、三角関数の合成で表現する方法なのだ。
それを細工した物になる。
ラプラス変換で微分方程式がなぜ解ける?(大阪大学:PDF)
| 改定前の怪しい記述 | ||
でも、結局の所・・・ 何を意味するのか、わからへん!! そこで、もう少し踏み込んで調べてみるのだが・・・ ヒルベルト空間って何やねん・・・ (--;; ぶ厚い数学の壁に阻まれた。 ヒルベルト空間を、わかりやすそうに説明しているサイトがあった。 EMANの物理学・量子力学・ヒルベルト空間 物理や数学を勉強している人なら「なるほど」と思うだろうが 私が理系なのは20世紀。過去の話で、全て忘却の彼方。 わかった気になっても「なるほど!」という感じではなかった。 ラプラス変換とは何なのか。どうやら、こんな事みたいだ。
じっくり数学を勉強できるのは老後なのかなぁと思ったりした。 いいかもしれない。ボケ防止のためには頭を使わねば (^^) |
複素数と交流回路
虚数。高校の数学で出てきた。
| 虚数とは |
|---|
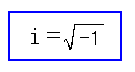 |
| -1の平方根の事を虚数という。 |
この虚数が交流回路の計算をする時に役立つというのだが その理由がわからへん・・・ なのだ。 一応、大学で複素数らしい事を習ったのだが・・・ 全く理解できへんかったのだ! 複素数の計算。頭の中で思い描きにくい。 暗記が嫌いな上、覚えられないため、理解しがたい世界だと思った。 理系だったのは20世紀。過去の話。 未来志向の私は、さっさと避けて通ろうと思った矢先 以下のサイトを発見した。 Dimensions 数学の散歩道 第5章 複素数 これを読んでみると・・・ 目からウロコなのらー (TT) 感激のあまりに涙が出そうなほどだった。
| 実数の世界 |
|---|
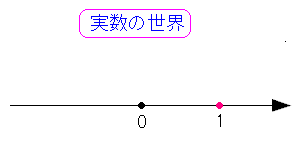 |
| 実数の世界は一直線上にある。 |
アルガンという数学者が、実数と虚数の間の幾何学性に気づいたみたいで 人工的に実数の直線に垂直の線を引いた。
| 人工的に実数の直線に垂直の線を引く |
|---|
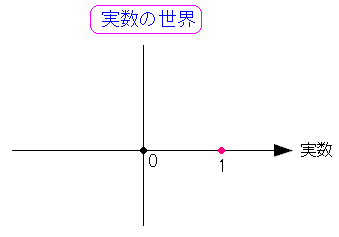 |
| 実数の世界を平面に広げた感じになる。 |
単純な掛け算を見てみる。
| 単純な掛け算 |
|---|
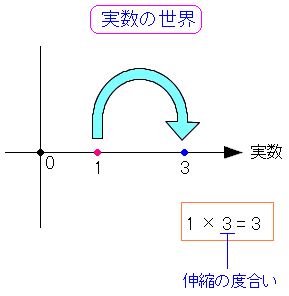 |
| 掛ける側の数字は、伸縮の度合を意味する。 |
そしてマイナスをかけた場合、次のように見える。
| マイナスをかけた場合 |
|---|
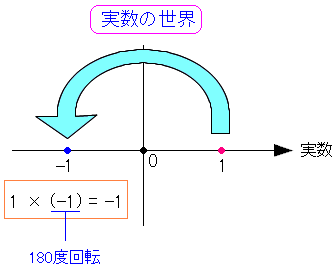 |
|
「-1」を掛けると、180度回転するのがわかる。 マイナスは180度回転する事を意味するのだ。 |
そして虚数の登場だ。
| 虚数とは実数に垂直な軸にある |
|---|
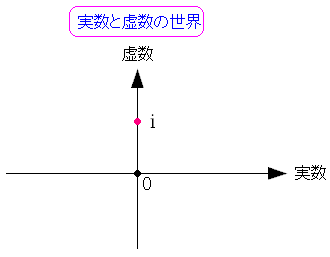 |
| 人工的に引いた直線上に虚数「i」を置く。 |
虚数「i」に虚数「i」を掛けるとマイナスの値になる。
| 虚数に虚数を掛けるとマイナスの値になる |
|---|
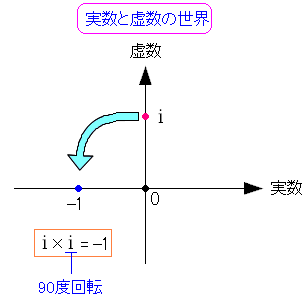 |
|
虚数「i」の2乗は「-1」なのだ。 なので虚数「i」は90度回転と見れば良いのだ。 |
ここではわかったのは マイナスは180度回転 虚数iは90度回転 掛け算は回転だというのがわかった。 ここでは、触れませんが、割り算は、反対方向の回転です。 さて、足し算はどういう意味なのか。
| 複素数の足し算 |
|---|
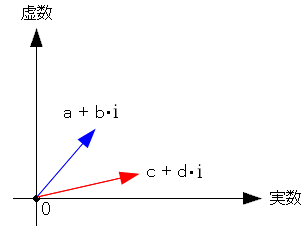 |
そして加算した結果、以下のようになる。
| 複素数の足し算の結果 |
|---|
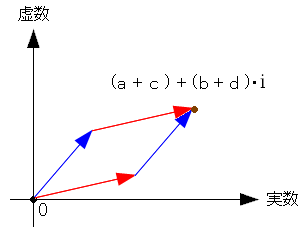 |
| 足し算を行なった場合、ベクトルの足し算と同じ結果になる。 |
ここでわかったのは・・・
ベクトルと同じ働きをする
なのだ。
複素数がベクトルと同じ働きをするのがわかった所で
複素数に複素数を掛けた場合を考えてみる。
| 複素数に複素数を掛けた場合 |
|---|
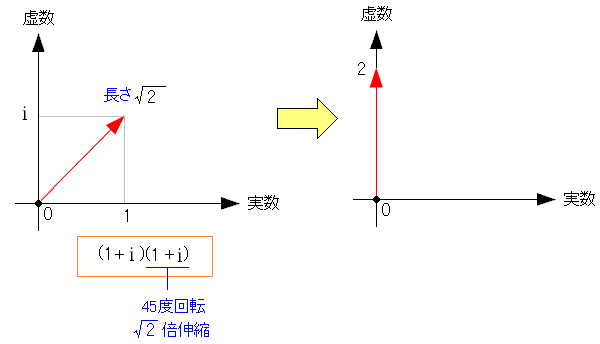 |
|
掛ける複素数は回転の役目と同時に、その複素数の大きさ(絶対値)は 伸縮の倍率をも意味する。 |
というわけで、ここまでのおさらいをすると 複素数の役割は 加算、減算はベクトル 乗算、除算は回転と伸縮 なのだ。複素数を使った交流回路の解き方
複素数を使って交流回路を解く方法。 電流・電圧をベクトルと考えれば、非常にわかりやすくなる。 まずは電流・抵抗・電圧を考える。
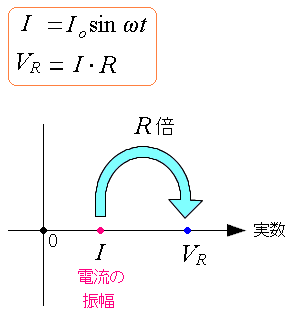
| 電流・電圧・抵抗について |
|---|
 |
|
振幅Iをベクトルと考え、実数上の軸の向きとする。 抵抗の場合、電圧と電流の位相は同じなので ベクトルとして考えると同じ向きになる。 電流にR倍(抵抗)を掛けた物が電圧になる。 |
次にコイルの場合を考える。
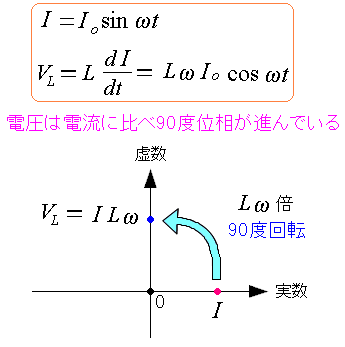
| 電流・電圧・コイルについて |
|---|
 |
|
振幅Iをベクトルと考え、実数上の軸の向きとする。 コイルの場合、電圧は電流よりも位相が90度進んでいる。 そのため、電圧は90度回転した上、Lω倍伸びたベクトルになる。 |
次にコンデンサーの場合を考える。
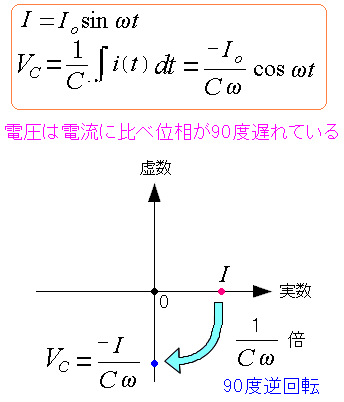
| 電流・電圧・コンデンサーについて |
|---|
 |
|
振幅Iをベクトルと考え、実数上の軸の向きとする。 コンデンサーの場合、電圧は電流よりも位相が90度遅れている。 そのため、電圧は90度逆回転したベクトルになる。 |
そしてRLC直列回路の場合を考えてみる。
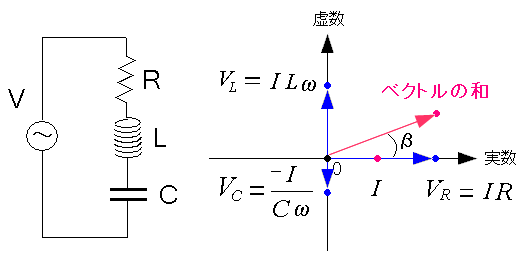
| RLC直列回路 |
|---|
 |
|
抵抗の電圧、コイルの電圧、コンデンサーの電圧。 それぞれベクトルと考える事ができる。 個々のベクトルの和が回路全体の電圧であり、電圧のベクトルになる。 この時、電流との位相のズレの「β」になる。 |
それらを複素数で表現すると以下のようになる。
| RLC直列回路を複素数で表現 |
|---|
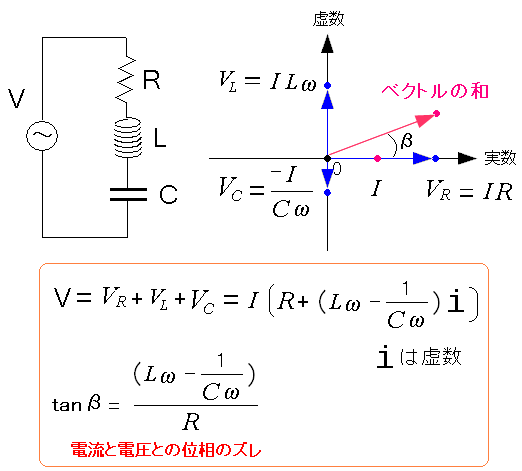 |
|
電圧は上の複素数で表せる。 位相のズレの「β」も表せる。 なんだか視覚的な上、微分積分を使うよりも扱いやすい感じがする。 |
さて、電圧の大きさだがベクトルの大きさを求めるのと同じだ。 ここでは複素数表現なので、複素数の絶対値を求めれば良い。
| RLC直列回路 電圧の大きさ |
|---|
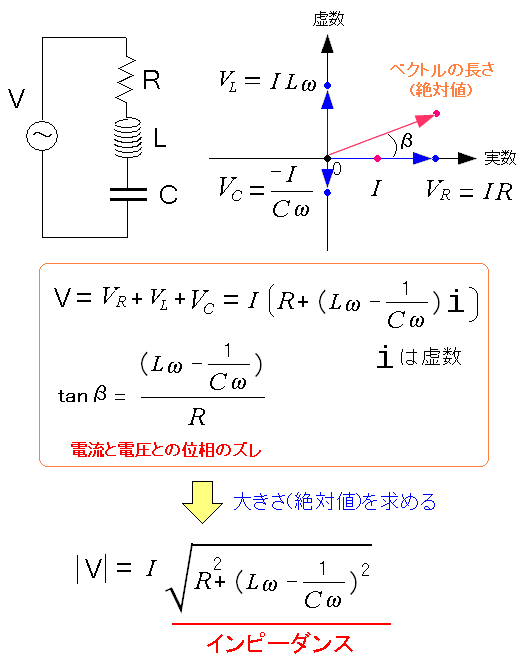 |
|
絶対値を使う事で電圧の大きさが出る。 そしてインピーダンスが簡単に求められた。 |
あっさりとインピーダンスが求まった! 微分積分を使うよりも手軽な感じがする。 だが、ラプラス変換と違い、過渡状態は見えない。 あくまでも定常状態だけ なのだ。
最後に(改定前) 電気回路の話。 UPS設定時の「力率とは何か」の疑問から始まって 色々、調べていくうちに、知らない事が噴出して とんでもない量になりました。編集して疲れた・・・。 変圧器の話、うず電流問題、うず電流を利用したIH調理器など 書き足らない所などがありますが、編集していて とても整理できる状態ではなくなりましたので この辺りで終わらせたいと思います。 「だったら電車の話に力を入れるな」と突っ込まれそうですが (^^;; 今回は電気回路ですが、電子回路の話や電子回路とLinuxなどを 絡めた話が書けたら、面白そうだなぁと考えています。
最後に(2016年の改定後) 怪しい記述や間違えた事を発見したため、改定に踏み切りました。 変圧器の話は書きませんでしたが、うず電流やIH調理器については 「システム奮闘記:その105」(電磁気学の基礎 電磁気学入門)で書きましたので ここでは触れない事にしました。 磁場と磁束密度の関係を知らなかったり、ラプラス変換の部分が怪しいなど いい加減な知識だったのにも関わらず、大筋では問題なのを見て 式さえ操作できたら、電気回路に関する解けてしまうという問題を認識しました。