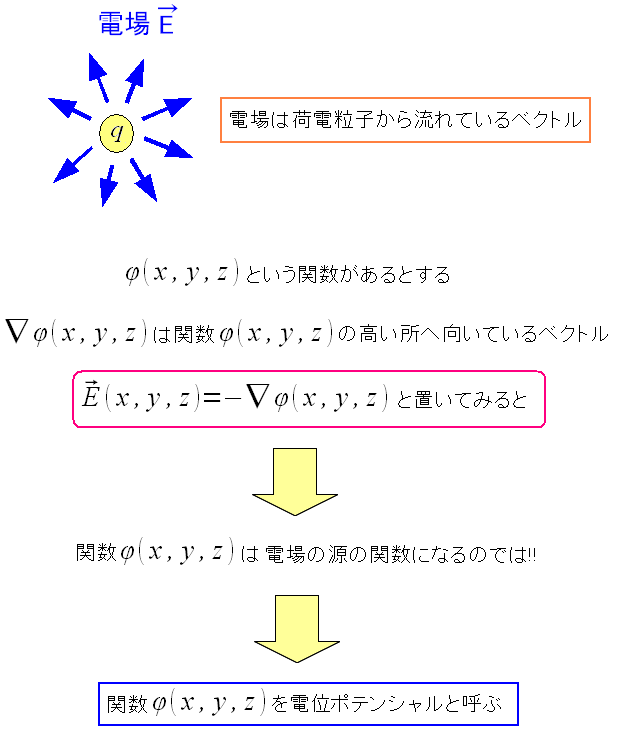
全微分や勾配の話で出てきたが、関数の勾配はベクトルだ。
もし、φ(x,y,z)の関数と、関数の勾配の式に当てはまると
φ(x,y,z)は電場の源になる関数になる。
先に答えを書くが、この時のφ(x,y,z)は電位ポテンシャルというのだ。
このことから考えると、電位ポテンシャルは「高さ」に相当するものなのだ
(注意)
ポテンシャルは「高さ」と言い切ると、語弊が出てくる。
ポテンシャルは潜在力を表わすだけに、間違いではないが
他にも要素があるので、「高さ」と言い切るわけにはいかないのだ。
システム奮闘記:その105
(2016年5月22日に掲載)
静電場と荷電粒子の仕事量
いきなり、電位ポテンシャルと言われても、何の事かわからない。 静電場上での荷電粒子がする仕事量(もしくは、される仕事量)の話から 電位ポテンシャルの話をすると見通しが良くなる。 まず「ポテンシャル」の言葉の意味を見てみる。 カタカナだと意味不明だが、英語だと「potential」になる。 日本語訳すると 可能性(潜在能力) なのだ。 先に答えを書くが・・ 貯蓄可能なエネルギーの指標 となのだ。
| ポテンシャルを力学で説明すると |
|---|
|
力学の場合、ポテンシャルは高さに該当する。 ボール(球)を高い所に物を持っていき、坂道を転がせば どんどん加速がついていく。 位置エネルギーが運動エネルギーに変換しているからだ。 ポテンシャルは貯蓄可能なエネルギーの指標という感じで捉えれば 捉えやすくなるのだ。 |
力学でのポテンシャルはわかった。 だが、それを電磁気に当てはめて、「高さに相当する」といってもピンとこない。 だが、次にように書けば、物事は考えやすくなる。 電場はベクトルであり 空間内に高い値を示す領域があるから 勾配にあたるベクトルがある 言葉だけだと、わかりにくいので、図にしてみた。
| 電位ポテンシャルは何なのか、電場から推測してみる |
|---|
 |
|
電場はベクトルなのだ。 全微分や勾配の話で出てきたが、関数の勾配はベクトルだ。 もし、φ(x,y,z)の関数と、関数の勾配の式に当てはまると φ(x,y,z)は電場の源になる関数になる。 先に答えを書くが、この時のφ(x,y,z)は電位ポテンシャルというのだ。 このことから考えると、電位ポテンシャルは「高さ」に相当するものなのだ (注意) ポテンシャルは「高さ」と言い切ると、語弊が出てくる。 ポテンシャルは潜在力を表わすだけに、間違いではないが 他にも要素があるので、「高さ」と言い切るわけにはいかないのだ。 |
数学的に考えたのだが、ここで知らねばならないのは物理的な意味であり どんな物理量なのかだ。 そこで物理に電位ポテンシャルが何なのかを見ていくのだが 回り道が必要になる。 荷電粒子が作る電場、荷電粒子が持つエネルギーの話などをした上で 電位ポテンシャルの話をするのだ。 まずは荷電粒子が作る電場の話から。
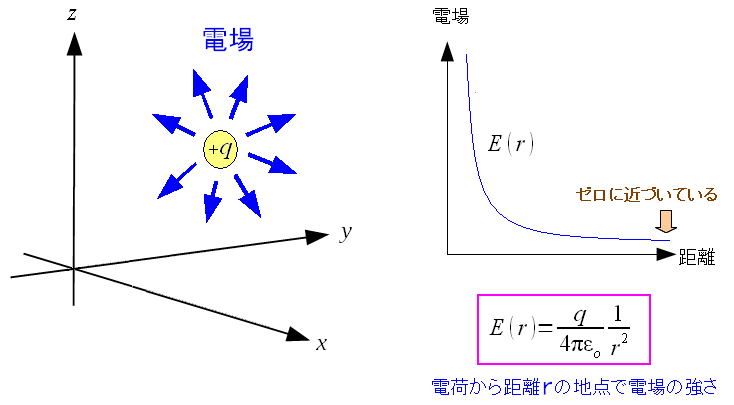
| 荷電粒子が作る電場 |
|---|
 |
|
電場とは、電荷によって空間に生じた変化の事だ。 電場の強さは、電荷量に比例し、かつ、距離の2乗に反比例する。 |
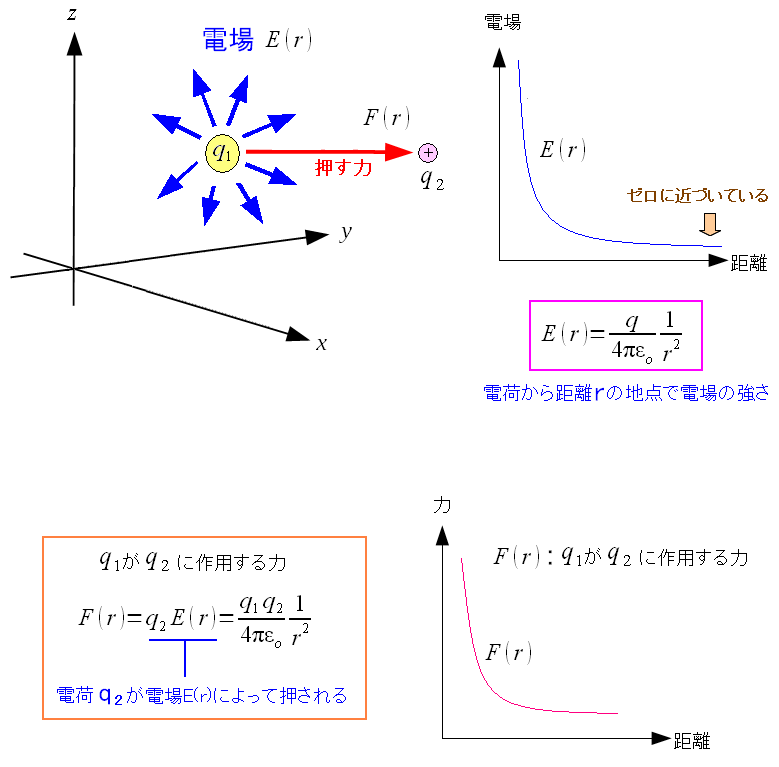
電場は、他の電荷に対して力の作用を及ぼす。 距離rの地点で、他の電荷(q2)があったとする。 その場合、どれくらいの力の作用が働くのか見てみる。
| 電場は、他の電荷に対して力の作用を及ぼす |
|---|
 |
|
q1とq2が同じ正電荷(もしくは負の電荷)の場合 q1の電荷から発生した電場は、q2の電荷に作用して q2を押す力(斥力)を生んでいる。 |
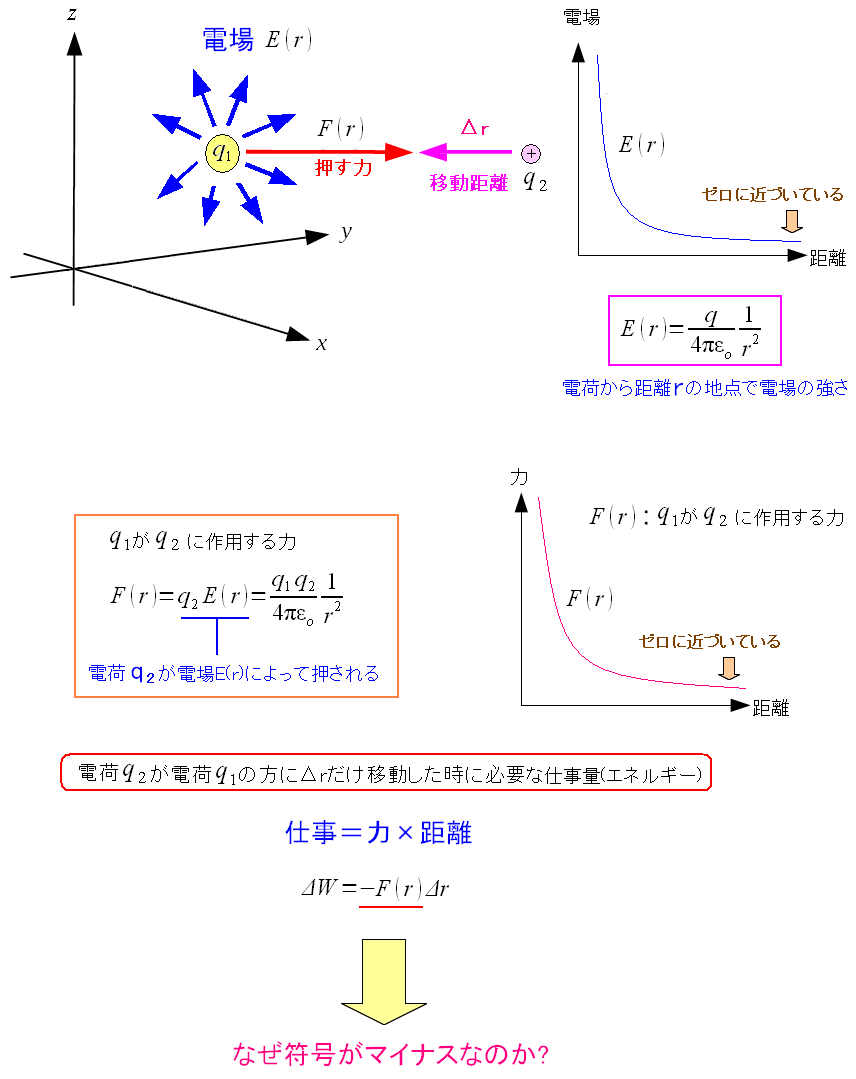
q2をq1の方向に近づけるとどうなるのか? その場合の仕事量は、どうなるのか考えてみる。 回りくどい説明だが、これも電位を説明するための準備なのだ。
| q2をq1の方向に近づけるとどうなるのか? |
|---|
 |
|
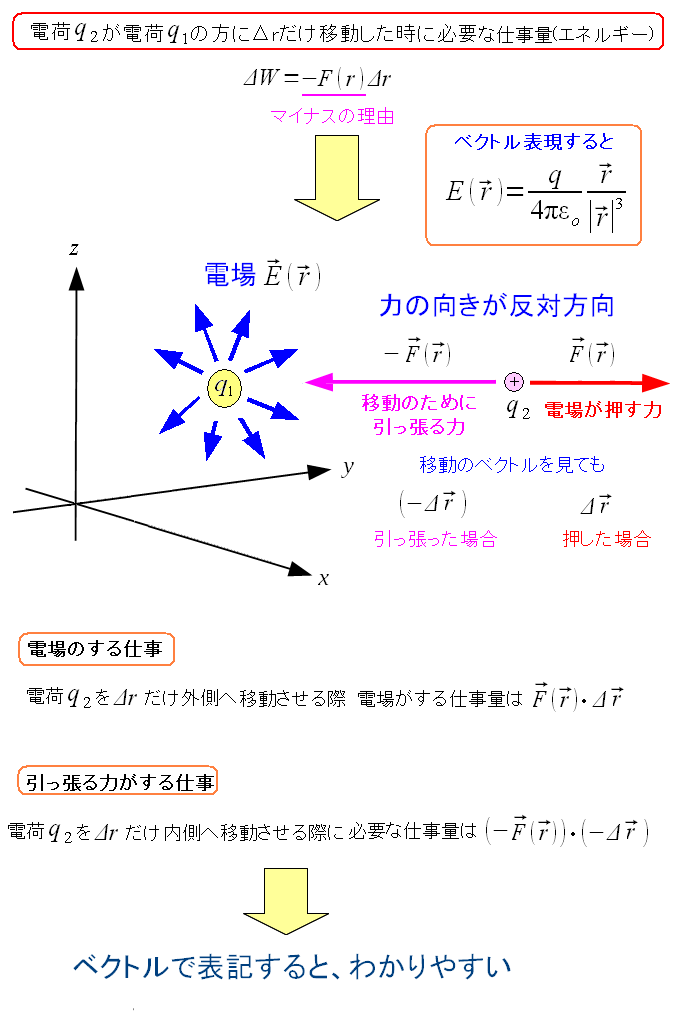
q2をq1に近づけた時、f(r)の力でq2が押されているため 同じf(r)の力で引っ張りあげる必要がある。 ここで疑問になるのは、仕事量がマイナスの符号が付く事だ。 力と距離の積が仕事量なので、f(r)×Δr(微小距離)が仕事量のはず。 必要な仕事量がマイナスとなれば、違和感があるのだ。 (注意) スカラーとベクトルの所で書きましたが 力はベクトル量で大きさだけでなく向きが重要になってくる。 向きはどっちかで、正・負が決まるため、注意が必要だ。 |
なぜ、マイナスの符号が付くのか。 ここで力の方向と向きの考え方が重要になってくる。 スカラーではなく、ベクトルで表現してみる。 荷電粒子の中心とした極座標系で考えると 荷電粒子から遠ざかる向きを正の方向になる。
| なぜ仕事量の式に、マイナスの符号が付くのか |
|---|
 |
|
力のf(r)は、外に向かっている力だ。 その力に対抗してq1の方に動かすため、力の向きが反対になるため スカラー表現だと、力の符号がマイナスというわけだ。 移動のΔrもスカラーの時は符号が見えない。 ベクトルにすると符号が見える。 外に向う方向だとΔrは正の値で、内側の場合、マイナスをつけるのだ。 単なる向きの問題で、プラスかマイナスかの符号がつくだけなのだ。 わからなくなった時は、ベクトル表記にすれば、見通しが良くなるのだ。 |
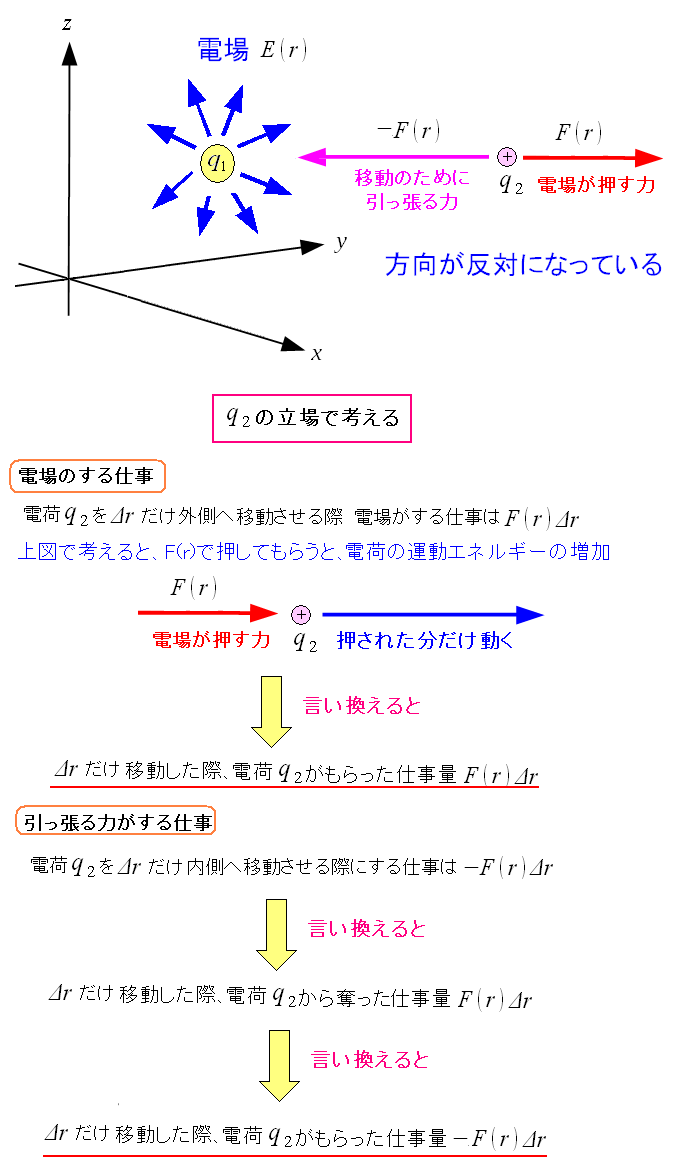
だが、実際の計算で、ベクトルとなれば、めんどくさい。 スカラー表記のまま計算したい。 そこで、なぜマイナスになるのか、もう1つの見方があるのだ。 電荷q2の立場になって見た場合なのだ。 q2は電場から仕事量をもらうか、奪われるかの違いで見てみるのだ。
| 仕事量の式にマイナスの符号が付く理由 |
|---|
 |
|
q1方向からf(r)の力でq2を押している。 q2は押されると、外側に向かって加速して走ったりする。 q2は仕事をもらっているのだ。 反対にq1に向かっているq2の場合、どんなに勢い良くq1方向に向かっても f(r)の力で押されて、どんどん減速してしまう。 q2は自分のエネルギーを失っている。つまり仕事量が奪われている事だ。 もらった仕事量はプラス。奪われた仕事量はマイナスと考えれば 合点がいくのだ。 |
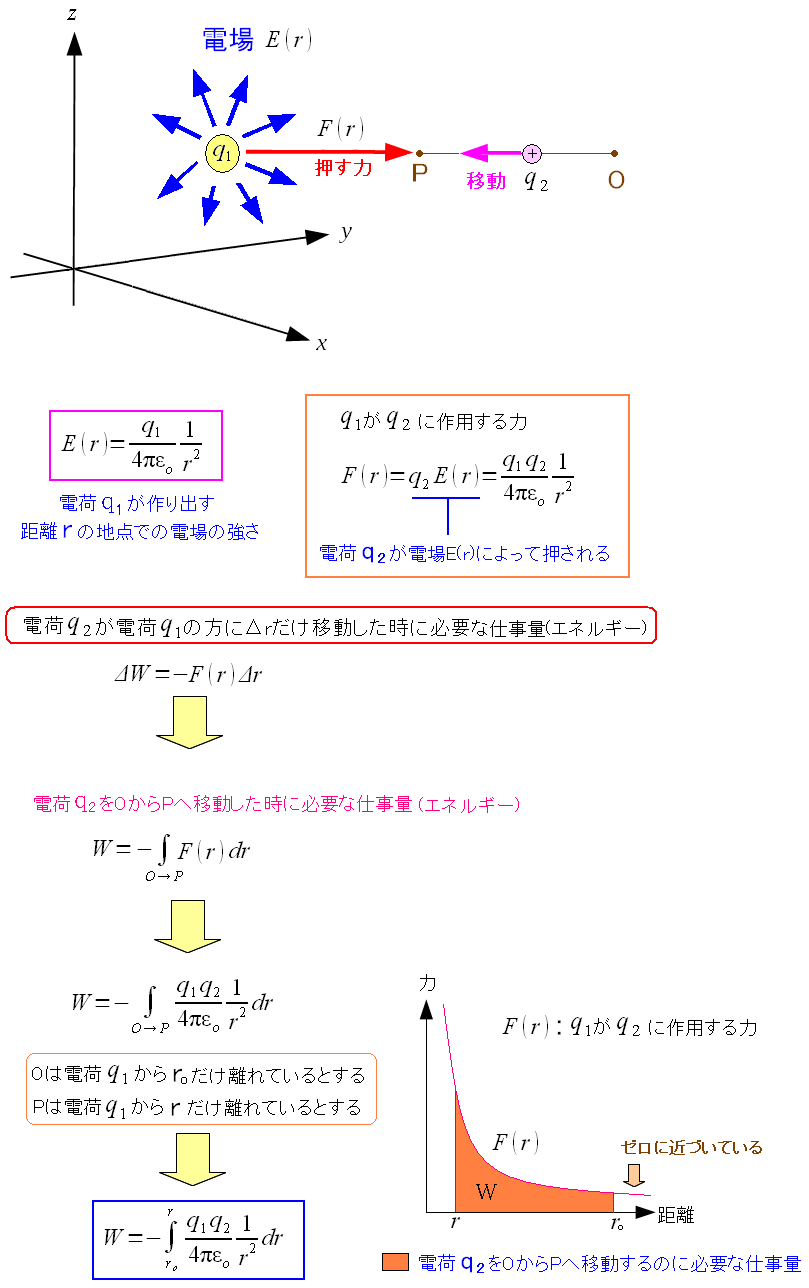
ここで出てきた 奪われた仕事量 が重要な事なのだ。 そして・・・ 奪われた仕事量は、どこへいくねん? なのだ。 奪われた仕事量は、貯蓄に回るのだ。その貯蓄が何かのかを見ていく。 まずは点Oから点Pへ移動した時に、q2が奪われた仕事量を求める
| 点Oから点Pへ移動した時に、q2が奪われた仕事量 |
|---|
 |
|
q2が奪われた仕事量が求まった。 |
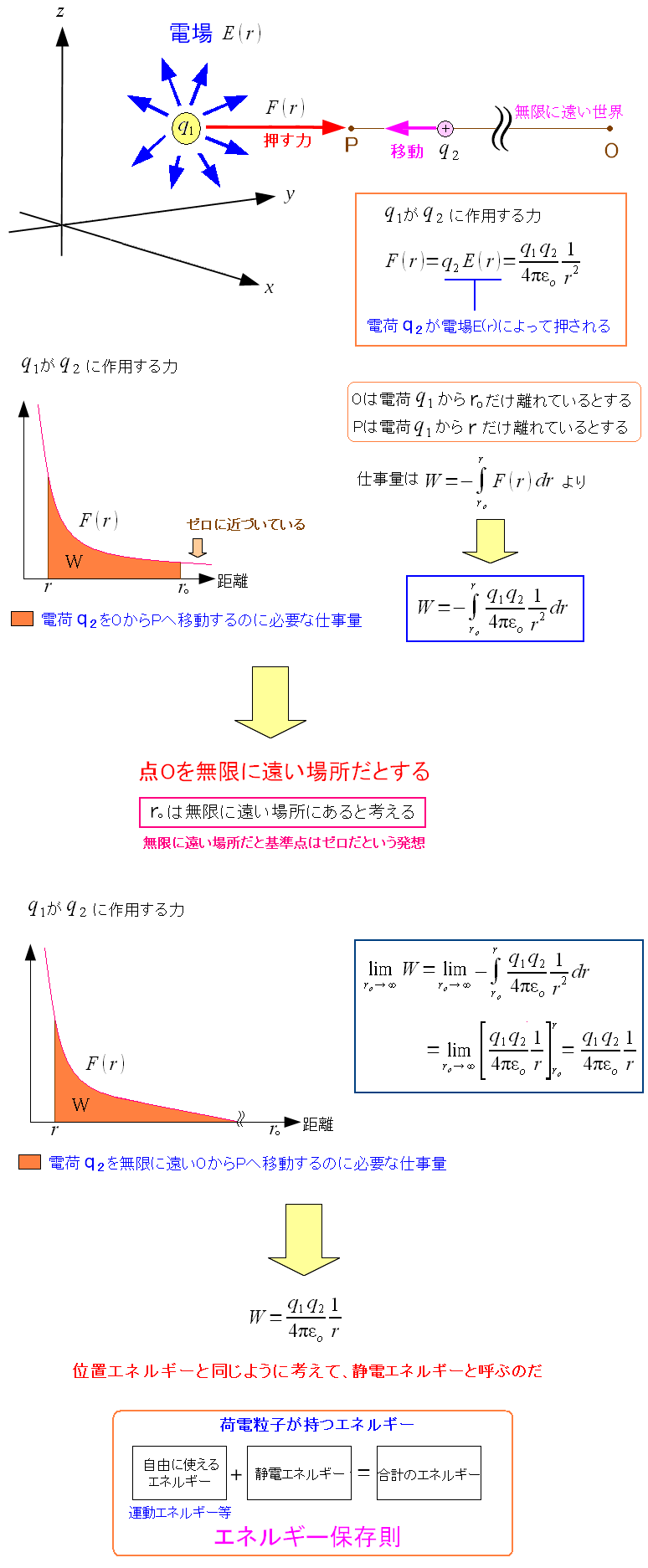
そこで点Oが遥か彼方の無限に遠い場所と考える。 q1が作る出す電場や、q1によって押される力がゼロの地点といえば 無限に遠い場所なのだ。 無限に遠い場所を基準として、どれだけの仕事量をq2から奪うのか 計算してみるのだ。
| 無限に遠い場所からq2を引っ張った時に奪われる仕事量 |
|---|
 |
|
q2が奪われる仕事とは、q2が無限に遠い場所から、q1からrまで移動する時 必要な仕事量を表す。 q2が奪われた仕事量は、静電エネルギーという形で貯蓄に回る。 力学の時と同様に、エネルギーの保存則が成り立つのだ。 |
仕事量が奪われる一方で、静電エネルギーがあがっていく 力学で出てきた運動エネルギーと位置エネルギーの関係と同じなのだ。
電位ポテンシャル
回りくどく静電エネルギーやエネルギー保存則の話をした。 これで準備ができた。 電場の中を電荷を引っ張った際、力学と同様に、荷物を引き上げるのと 同じことをしている。
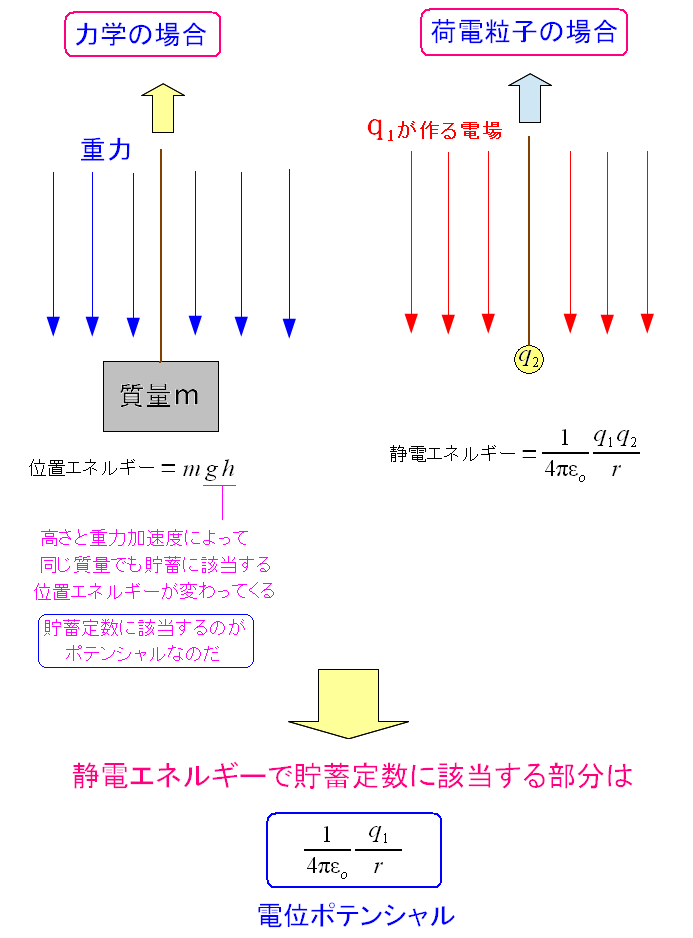
| 静電エネルギーとは電荷q2のエネルギーの貯蓄の事 |
|---|
 |
|
力学の場合、物を引き上げた場合の位置エネルギーは m g hになる。 この時、位置エネルギーの量を決めるのは、持ち上げる物体の質量(m)だけでなく 持ち上げる高さ(h)と、重力加速度(g)になる。 貯蓄可能なエネルギー量の知るための指標に該当するのが「g h」で 物を高く上げる事で、位置エネルギーは増加するし 物を上げる高さは同じでも、重力加速度が大きい木星や土星に行けば 位置エネルギーは大きくなるのだ。これがポテンシャルに相当する。 q1が作る静電場の場合に、外部から荷電粒子を持ってきた場合 荷電粒子が貯蓄可能なエネルギー量の指標が求められる。 それが電荷q1が作る電位ポテンシャルというものになるのだ。 |
わかったような、わからんような感じなのだが、電位ポテンシャルは 電磁気の話で重要なので、知らないと、この先に進めないのだ。 電磁気に限らず、乾電池が1.5Vとか、コンセントの電圧が100Vというのも 電位ポテンシャルなのだ。 次に電位ポテンシャルと電場の関係式を見てみる。 話の最初の所で、電場の源になる関数を電位ポテンシャルと書いたのだが まさに以下の関係式が成り立つのだ。
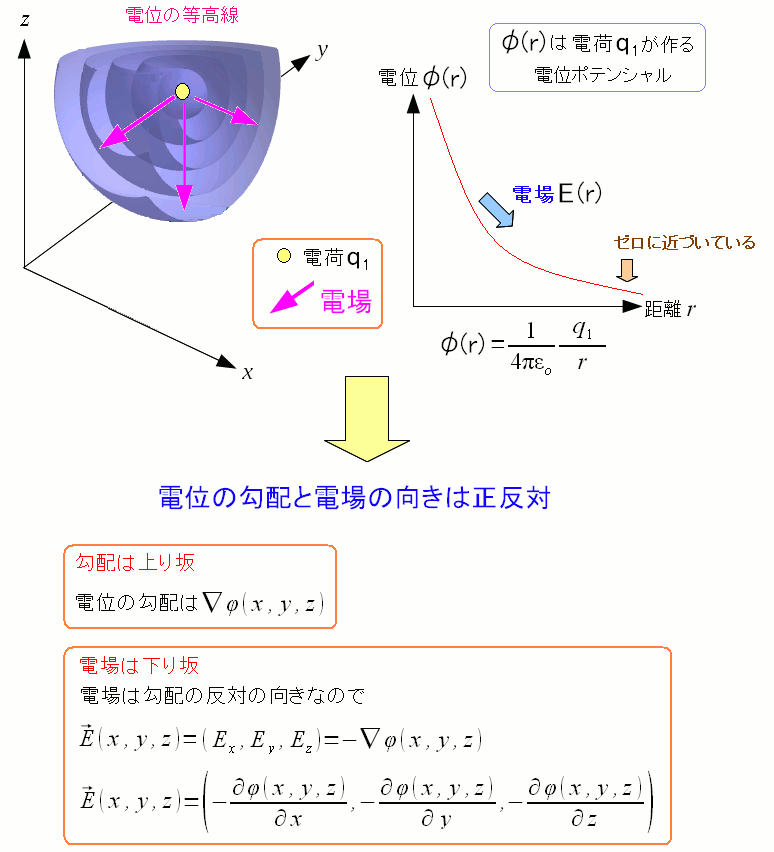
| 電位ポテンシャルの勾配は電場 |
|---|
 |
|
電位ポテンシャルの勾配は電場と言いたいのだが、勾配は高い方向なので、逆になる。 だが、最初に電場は、正の電荷から外に向かって流れるとしている。 そのため電場と勾配の向きが正反対になってしまうため 勾配にマイナスをつけて、電場を表しているのだ。 |
ところで電位ポテンシャルの事を
スカラーポテンシャル
と言う。
その理由は電位は数値で表しているからだ。
位置エネルギーも同じスカラーポテンシャルになる。
| スカラーポテンシャル以外にもポテンシャルがある |
|---|
|
スカラー(数値)以外にもポテンシャルはある。 ベクトルで表すポテンシャル、即ち、ベクトルポテンシャルだ。 それについてはベクトルポテンシャルの所で説明しています。 |
電位、電場の足し合わせ
ところで荷電粒子は1つだけとは限らない。 近くに複数ある場合だって考えられる。 その場合の電場と電位だが 単純に足し合わせれば良い のだ。
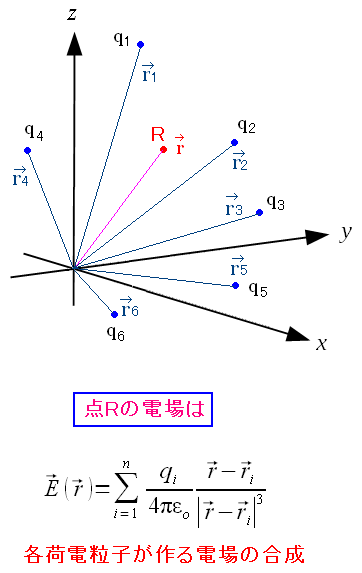
| 複数の荷電粒子がある場合の電場の重ね合わせ |
|---|
 |
|
各荷電粒子が作る電場を足し合わせた物が、その位置での電場になる。 電場の場合、ベクトルなので方向を持っている。 なので実際に足し合わせる際は、方向を考慮して計算する必要がある。 |
そして電位も足し合わせれば良いのだ。
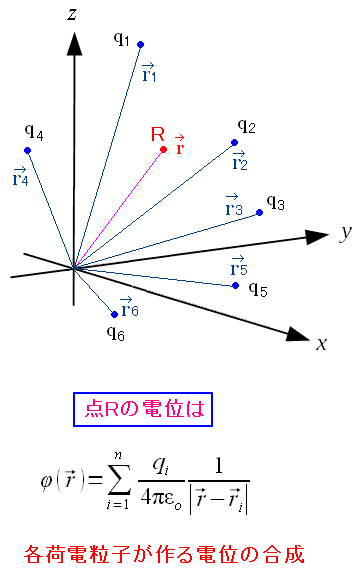
| 複数の荷電粒子がある場合の電位の重ね合わせ |
|---|
 |
|
各荷電粒子が作る電位を足し合わせた物が、その位置での電位になる。 スカラーなので、単純に足し合わせるだけで良いのだ。 |
ところで、複数の電荷が作る電場を求める際、電場の足し合わせを求めるよりも 電位の足し合わせを求めた後、微分して電場を求めた方が計算が楽なのだ。 電位の場合はスカラーポテンシャルで方向を持っていない。 だが、電場は方向があるため、方向を考慮した上で 足し合わせを行う必要があるからだ。 それを頭に入れておけば、何らかの実験などで電場を求める際、 計算が楽になったりするのだ。
電磁気学入門の目次
| 電磁気学入門:目次 | |
|---|---|
| スカラーとベクトル | 簡単なスカラーとベクトルの話です。 ベクトルは方向と大きさを持つ量。方向という量持っているだけに注意が必要です。 |
| 静電気の発見からクーロンの法則 | 今でこそ当たり前の静電気や導体、絶縁体、電荷など どういう経緯で発見し、クーロンの法則まで至ったのかの話です。 |
| クーロン力、電場、近接作用 | 4つの力のうち、クーロン力の位置づけ 電荷が作り出す作用の電場。近接作用の話です。 |
| 微分、全微分、方向微分 | 簡単な微分、全微分、方向微分の話です。 ここをしっかり押さえないと、電磁気の数式の意味が わからなくなります。 |
| ベクトル解析 |
電磁気に必要なベクトル解析の話です。 勾配(grad)、2次元のグリーン定理 ストークスの定理の話です。 |
| 電位ポテンシャル | 電位ポテンシャルです。勾配と電場の関係を使って説明しています。 |
| 電気双極子 |
電気双極子の話です。 物質中で起こる分極を理解するのに必要です。 |
| ガウスの法則 | ガウスの法則の積分形、微分形の話です。 |
| ポアソンの方程式、ラプラス方程式 |
ポアソンの方程式、ラプラス方程式の話です。 単に電荷分布から電位を求めるだけの話にとどまらない 奥が深い分野です。ポテンシャル論、デルタ関数 グリーン関数、固有値問題について触れています。 |
| 静電場と渦なしの法則 |
静電場で、電荷を1周させた時の仕事はゼロ 微分形と微分形の渦なしの法則の話です。 |
| ビオサバールの法則 |
電気と磁場の関係の発見の話から ビオ・サバールの法則が導かれるまでの話です。 |
| 磁気双極子 |
磁気双極子の話で、回転電流になります。 物質中の磁場の話にも関連します。 |
| アンペールの法則 |
アンペールの法則の話です。 積分形・微分形だけでなく、閉回路に流れる電流が作る 磁気双極子の話なども書いています。 |
| ローレンツ力 |
磁場中を移動する電荷にかかる力(ローレンツ力)の話です。 ローレンツ力は相対性理論が絡んでいる事も紹介しています。 |
| ファラデーの誘導起電力の法則 | ファラデーの誘導起電力の話です。 |
| うず電流を使った簡単な物理実験 | 電力計に使われるアラゴの円盤。 そしてIH調理器で熱するために発生させる、うず電流は レンツの法則から電流が発生する原理を応用した物だ。 アラゴの円盤の実験と、IH調理器を使った実験です。 気分転換で読んでください。 |
| ベクトルポテンシャル |
わかりにくいベクトルポテンシャルの話です。 電位は電荷が作る電気のポテンシャルだが ベクトルポテンシャルは電流が作る磁場のポテンシャルの話です。 |
| オームの法則の微分形 | 微小領域でのオームの法則の話です。 |
| マックスウェルの方程式 |
4つのマックスウェルの方程式を書いています。 電場と磁場の変化を図にする事で rotの回転の意味も理解できます。 |
| ゲージ変換 |
ゲージ(gauge)は物差しの意味です。 マックスウェルの方程式をE(電場)とB(磁場)の関係式から φ(電位ポテンシャル)とA(ベクトルポテンシャル)の関係式に 書き換える際、ゲージ変換が使われます。 ゲージ変換の役目を書きました。 |
| 電磁波 |
マックスウェルの方程式から電波が伝わる様子を 視覚的に見てみる話です。 |
| 回転のrotはベクトルの微分 |
ベクトル解析や渦なしの法則で出てくるrotは ベクトルの微分という話です。 |
| 電磁気学の単位系 | 電磁気学の単位系の話です。 物理量の単位系の指数を見る次元解析 電磁気学の歴史と単位系の変遷について触れました。 |
| 電気泥棒:電気と法律の話 |
電気は物体なのか、無形物なのか。 明治時代に、電気を無断で使った場合、物か、そうでないかで 窃盗罪になるかどうかが裁判で問われました。 ちょっとした科学と法律の話です。気分転換で読んでください。 |
| 数ベクトルと基底ベクトル | ベクトルの話です。 矢印だけがベクトルでない事。 数ベクトルと基底ベクトルの違いの話です。 多様体、反変・共変ベクトルを理解するのに必要です |
| 多様体 | 空間を一般化した話です。 ▽(ナブラ)の正体に迫まります |
| 外積代数 |
外積、テンソルについて書いています。 極性ベクトル、軸性ベクトル 外積は行列で、ベクトルは見せかけの姿だった話です。 |
| ベクトルの双対関係 |
反変ベクトル、共変ベクトル、双対関係 ベクトル解析、外積代数の話 外積、テンソルについて書いています。 |
| ローレンツ力と相対性理論 |
磁場は電場の相対論的効果だった話です。 ローレンツ力を使って、導線が作る磁場を使って説明です。 |
| 微分形式 |
多様体の話の続きです。 座標に依存しない形での関数やベクトルの微分の話です。 ガウスの法則、アンペールの法則、マックスウェルの方程式が 鮮やかな形で表現できます。 ∇(ナブラ)の正体もわかります。 |
| 物理と対称性 |
マックスウェルの方程式をよく見ると対称性があります。 物理の方程式と対称性を数学的な観点でみると 意外なつながりがあるという話です。 |
| マックスウェルの応力 |
電気力線を弾性体(ゴム)とみなして、力の伝わり方などを 説明した考え方です。 |
| 電場エネルギー | 電場が持つエネルギーの式を導いた話です。 |
| 磁場エネルギー |
磁場が持つエネルギーの式です。 手抜きの説明と、直流RL回路を使った説明を書きました。 |
| ポインティングベクトル |
電磁エネルギーの流れ「ポインティングベクトル」の話です。 電磁波でもエネルギー保存則が成り立つ話から ポインティングベクトルを導いています。 |
| 電気エネルギーは導線の外を伝わる |
導線の外を電気エネルギーが流れる話です。 私が誤解した事、その誤解を解いていく過程を紹介しながら 「目からウロコ」にたどり着いた話です。 |
| 物質中の電場 | 物質中の電場の話です。 分極の話をしながら、物質中の電場の話をします |
| 物質中の磁場 | 磁性の話をしながら、物質中の磁場の話をします |
| 物質中のマックスウェルの方程式 | 物質中でもマックスウェルの方程式が成り立つ話です。 |
| 導体に侵入する電磁波 |
導体に侵入する電磁波が減衰していく話です。 表皮効果と同じ「表皮の厚さ」が出てきます |
| 表皮効果 |
目的の表皮効果の話です。 マックスウェルの方程式を解きながら 交流電流の周波数を上げると、表面にしか電流が流れなくなる話です。 |