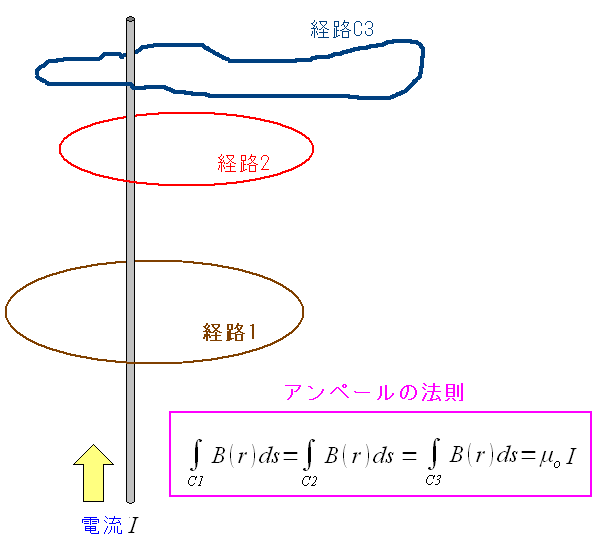
閉じた経路に沿って磁場を足し合わせた結果が
閉じた経路を貫く電流の和に比例するというのだ。
真空中の場合、閉じた経路の形状に関わらず、誘磁率(μo)と電流(I)の積になるのだ。
本当に経路の形状に依存しない事を、あとで数値計算で示しています。
システム奮闘記:その105
(2016年5月22日に掲載)
アンペールの法則
アンペールの法則とは以下の事を言う。
| アンペールの法則 |
|---|
 |
|
電流と電流が作る磁場との関係式だ。 閉じた経路に沿って磁場を足し合わせた結果が 閉じた経路を貫く電流の和に比例するというのだ。 真空中の場合、閉じた経路の形状に関わらず、誘磁率(μo)と電流(I)の積になるのだ。 本当に経路の形状に依存しない事を、あとで数値計算で示しています。 |
この法則が正しいかどうかの実験が行なわれた時期を探すのだが 西暦1820年: 電磁気学の夜明け「電流の磁気作用の発見」他 電流が作る磁場(物理準備室) 物理学B 第6章 定常電流と静磁界(慶応大学) エレクトロニクス科学史 エールステッドとアンペールによって統一された電気学と磁気学 エルステッドの発見とアンペールの法則 電気の世紀へ < 啓蒙の時代から 3電気と磁気へ >(PDF) 物理の歴史(電磁気) これだけ調べたりしても・・・ わからへん!! なのだ。 1820年、ビオサバールの法則の発表と同時に、アンペールの法則も発表されたが アンペールの法則は、他にもあるやん!!
| 右ねじの法則 |
|---|
 |
|
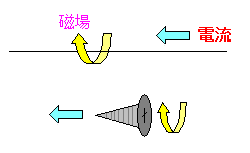
右ねじの法則は、アンペールが発見したのだ。 電流が流れる向きで、反時計周りになっている。 正の方向への回転になっている。 |
そして2本の導線に電流を流した実験もアンペールが行なった。
| 2本の導線に電流を流した実験 |
|---|
 |
|
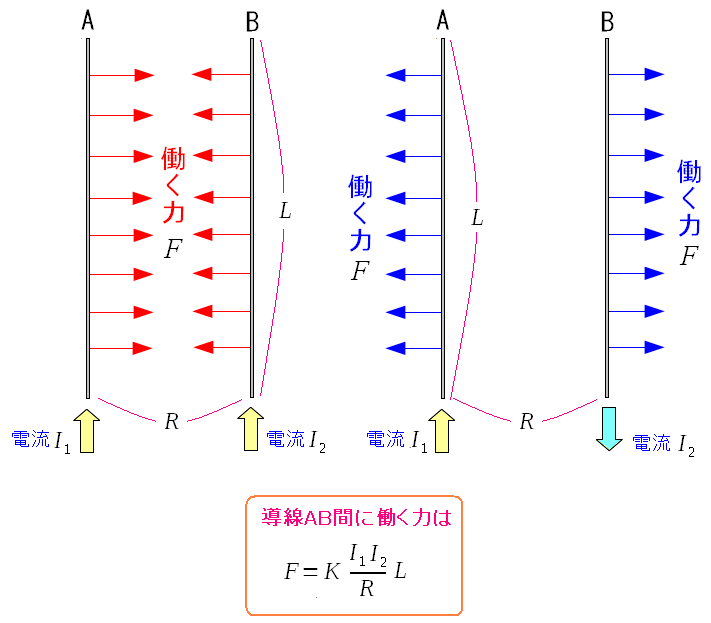
2本の導線に、同じ向きに電流を流すと引力が生まれる。 異なる向きに電流を流すと斥力が生まれる。 引力(斥力)の力はお互いの電流の積に導線の長さを掛けた物に比例するのだ。 |
というわけで、混乱してきたのだ。
そのため・・・
歴史の話を調べるのは断念・・・
なのだ。
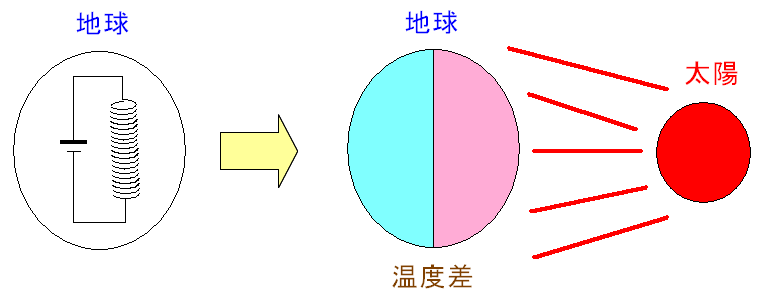
ところでアンペールは地球磁場が発生する原因として
地球内部に巨大な電磁石があると考えたのだ。
| 地球内部には電磁石があるという説 |
|---|
 |
|
ギルバートが地球は磁石と唱え、アンペールは地球内部に 巨大な電磁石があると考えた。 電流発生源は、太陽の熱で、太陽光が当たる部分(昼間)と当たらない場所(夜)との 温度差によって電流が発生していると仮説を立てた。 アンペールの仮説は外れたが、アンペールの仮説をキッカケに 温度差による電流発生の原理の研究が始まり 1821年にゼーベックによって発見され、ゼーベック効果と呼ばれているのだ。 |
そんな時代に、ゼーベック効果が発見されていたとは知らなかった。
静磁場中のガウスの法則
まずは静電場中のガウスの法則を、おさらいしてみる。
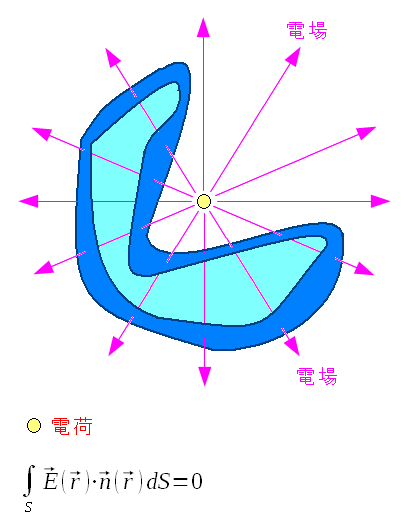
| 静電場中のガウスの法則 |
|---|
 |
|
静電場中にある閉空間内に電荷がない場合は 空間に入る電場と出ていく電場の量が同じなので 合計するとゼロになるという法則だ。 |
磁気双極子のない閉空間でも、磁束密度の流入と流出が同じになり ゼロになるのだろうか。
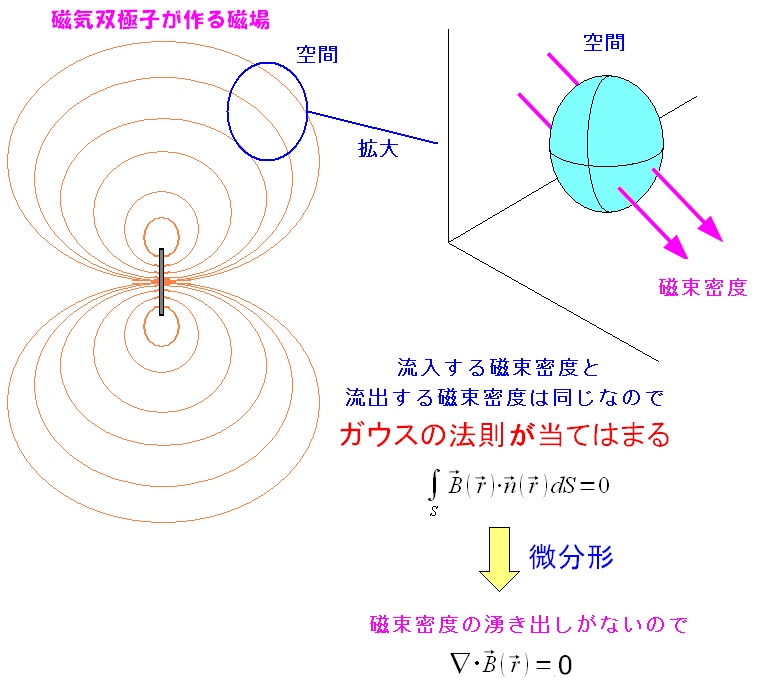
| ガウスの法則が静磁場でも成り立つのか? |
|---|
 |
|
静磁場中の閉空間を貫く磁束密度の合計は 流入も流出も同じなので、結果はゼロになる。 静電場と同様、静磁場中でもガウスの法則は成り立つのだ。 |
ここでは、敢えて、磁気双極子を含む空間は取り上げない。
静磁場中の、渦なしの法則
今度は静磁場中の渦なしの法則を見てみる。 考える空間(経路)は、磁気双極子を含まない領域とする。
| 磁気双極子を含まない静磁場空間で、渦無しの法則が成り立つ |
|---|
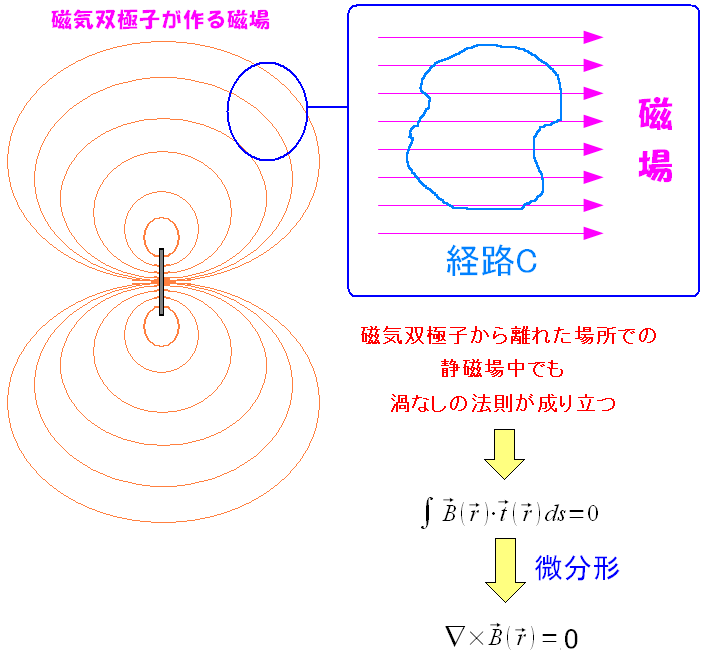 |
| 静磁場でも、渦無しの法則が成り立つ。 |
本当に、磁気双極子を含まない静磁場空間で、渦無しの法則が成り立つのか? そこで確かめてみる事にした。 ここでは、わかりやすくするため、3次元空間ではなく、2次元の平面で考える事にした。
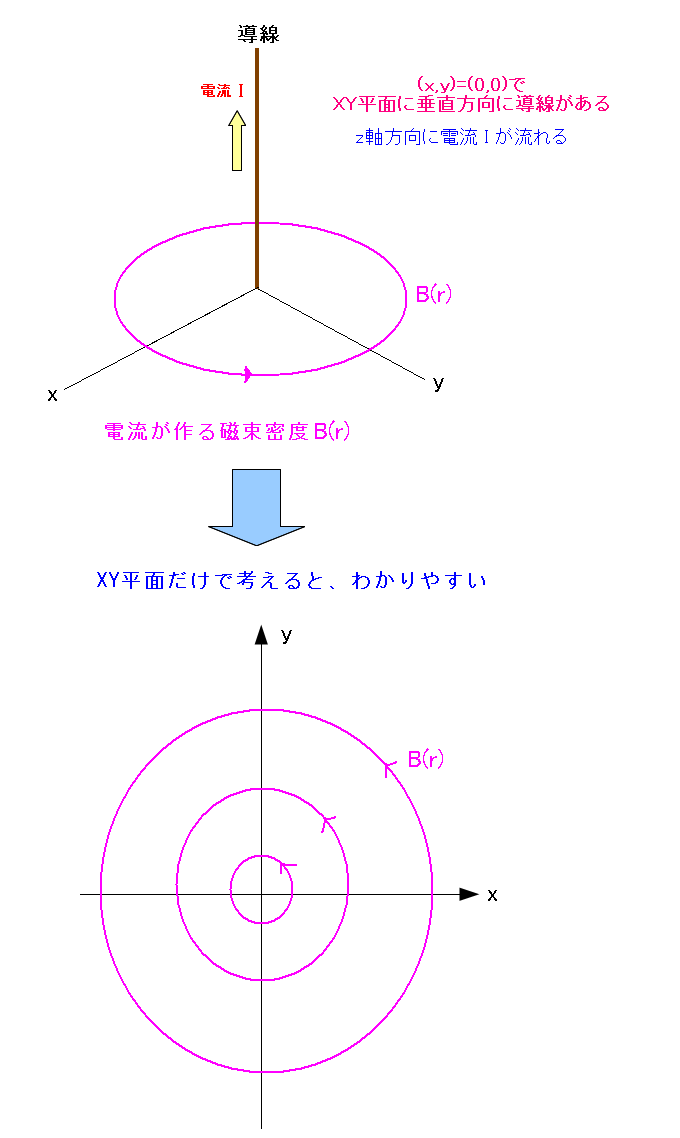
| 2次元(平面)で考えてみる |
|---|
 |
|
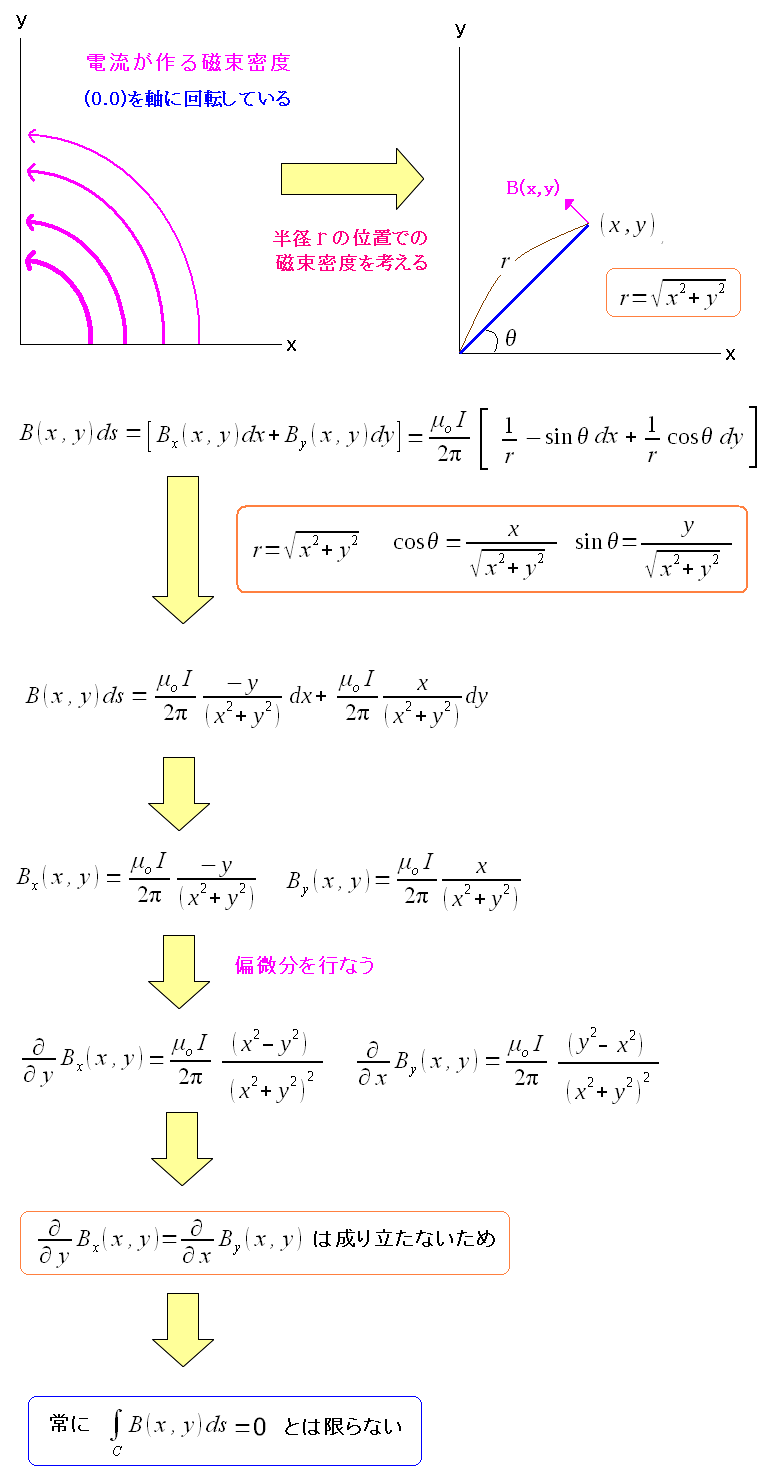
導線がZ軸にあり、Z軸方向に電流が流れている場合 磁束密度はXY平面上を反時計周りの方向で発生するのだ。 2次元にする事で、わかりやすく、かつ、あとの計算を楽にするのだ。 |
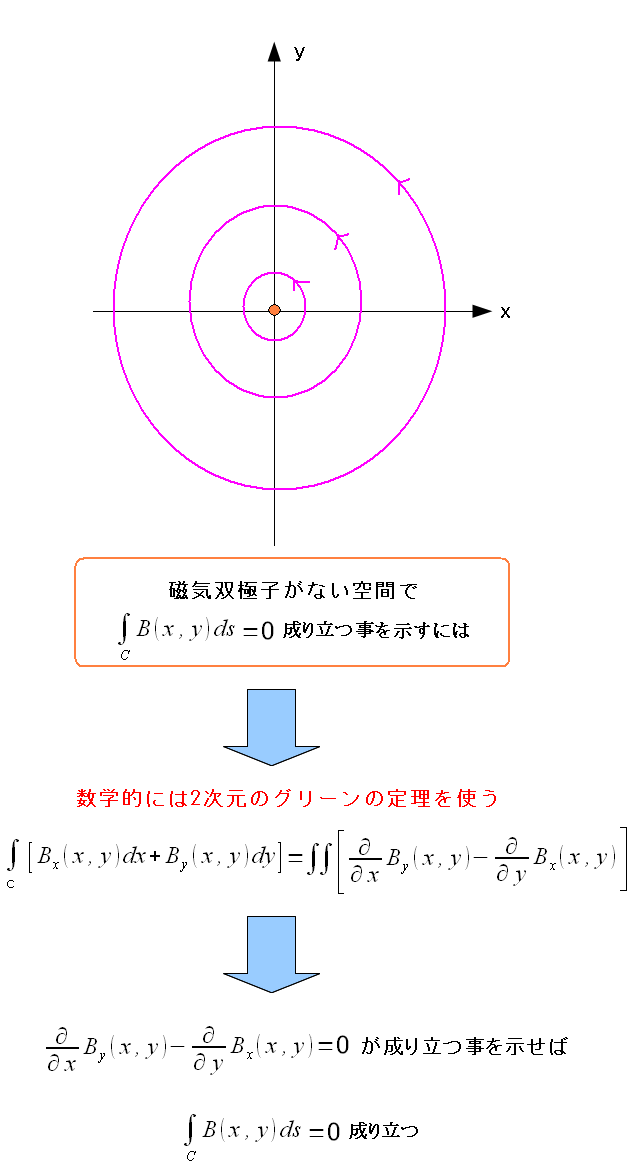
まずは数学的に見てみる事にする。 2次元のグリーンの定理を使えば良いのだ。
| 数学的には2次元のグリーンの定理で確かめる事ができる |
|---|
 |
|
ここにきて、ストークスの定理の前段階に出てきた 2次元のグリーンの定理が活躍する。 |
2次元のグリーンの定理を使って確かめてみる。
| 2次元のグリーンの定理で渦なしの法則を確かめてみる |
|---|
 |
|
2次元のグリーンの定理を使ったみたが 渦なしの法則が成り立つとは限らない。 磁束密度の式は、原点(0,0)が特異点になっているため それが原因で2次元のグリーンの定理が成り立たない状態だ。 |
でも、往生際の悪さは天下一品の私。
なので・・・
近似計算すればエエやん!!
という事で、数値計算で近似値を出してみる事にした。
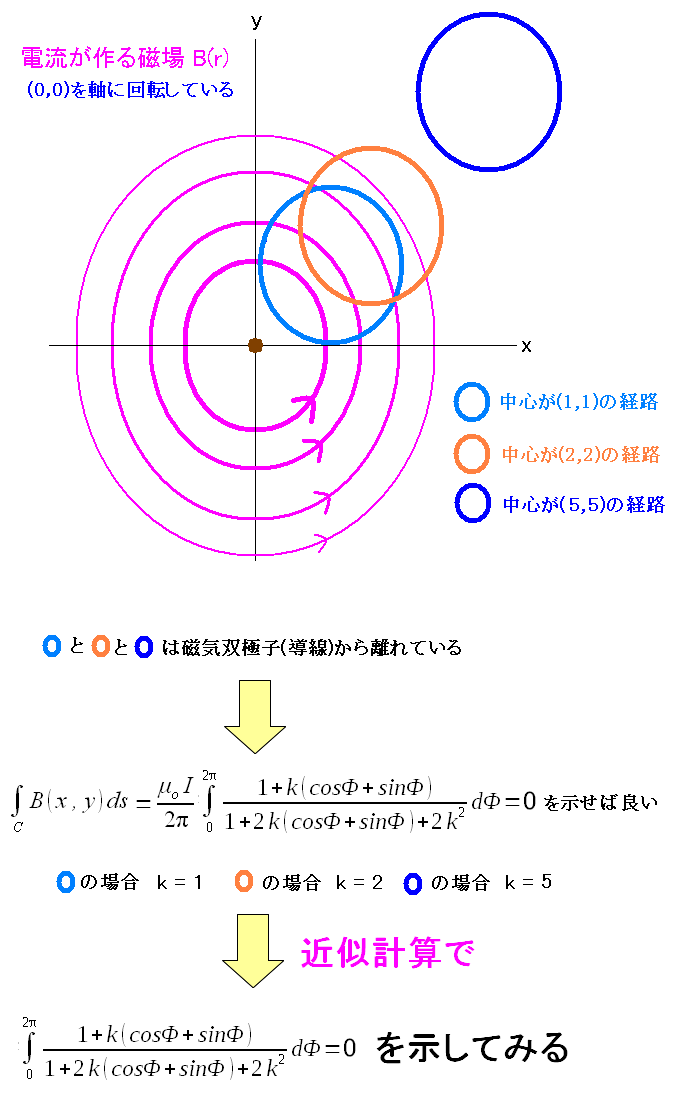
| 3つの円経路で近似計算してみる |
|---|
 |
|
導線をまたがない、円経路だと、円経路の位置に関係なく 経路積分の値がゼロになる事を示せば良いのだ。 |
そこで以下の単純なプログラムを書いてみた。
| 数値計算のプログラム |
|---|
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int main(void)
{
double fai , k , pi , pi2 , delta , dfai ;
double total ;
pi = 3.1415926 ;
pi2 = pi*2.0 ;
k = 1.0 ; /* ここの数値を変える */
dfai = 0.00001 ;
total = 0.0 ;
for ( fai = 0.0 ; fai < pi2 ; fai += dfai )
{
delta = ( 1.0 + k * (cos(fai) + sin(fai) ) ) /
( 1.0 + 2.0 * k * (cos(fai) + sin(fai)) + 2.0 * k*k) ;
total += (delta * dfai);
}
printf("total = %lf \n",total);
return(0);
}
|
早速、計算したら・・・
期待した通りの結果が出た!!
のだ。
| 数値計算の結果 | |
|---|---|
| k = 1.0 | 0.000002 |
| k = 2.0 | 0.000001 |
| k = 5.0 | 0.000000 |
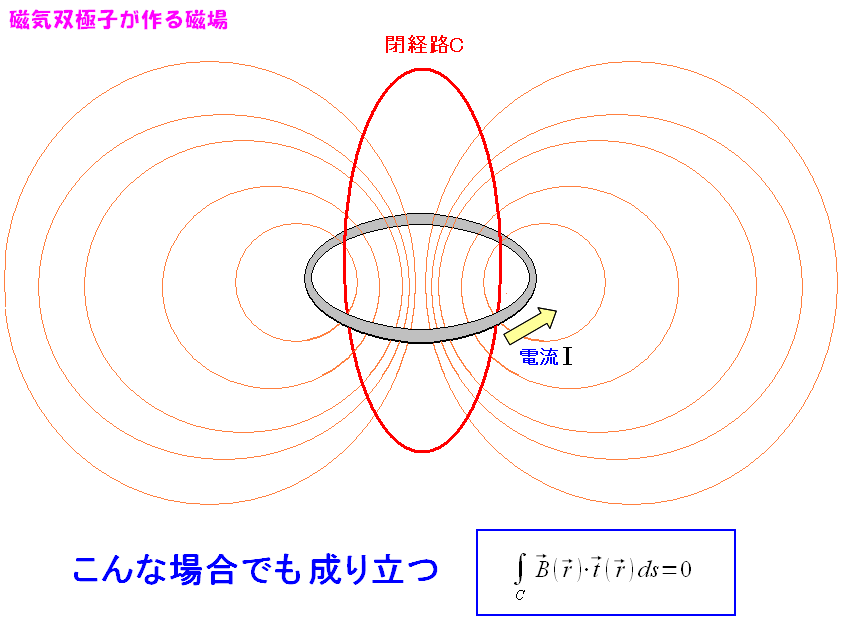
計算の精度は粗いものの、静磁場中では 導線から離れた閉経路Cを1周させた場合 経路積分はゼロになる事が示せた!! のだ。 そして磁気双極子を構成する円回路の中に、閉曲線があった場合でも成り立つ。
| 磁気双極子を構成する円回路の中に、閉曲線があった場合 |
|---|
 |
|
導線をまたがないので、上図の場合でも、渦無しの法則は成り立つ。 近似計算すれば良いのだが、そこまで計算力はないので 近似計算は、許してチョンマゲなのだ。 |
だが、磁気双極子を作る円形の回路と閉回路が交差した場合 話が変わってくるようだ。
| 磁気双極子を作る円形の回路と閉回路が交差した場合 |
|---|
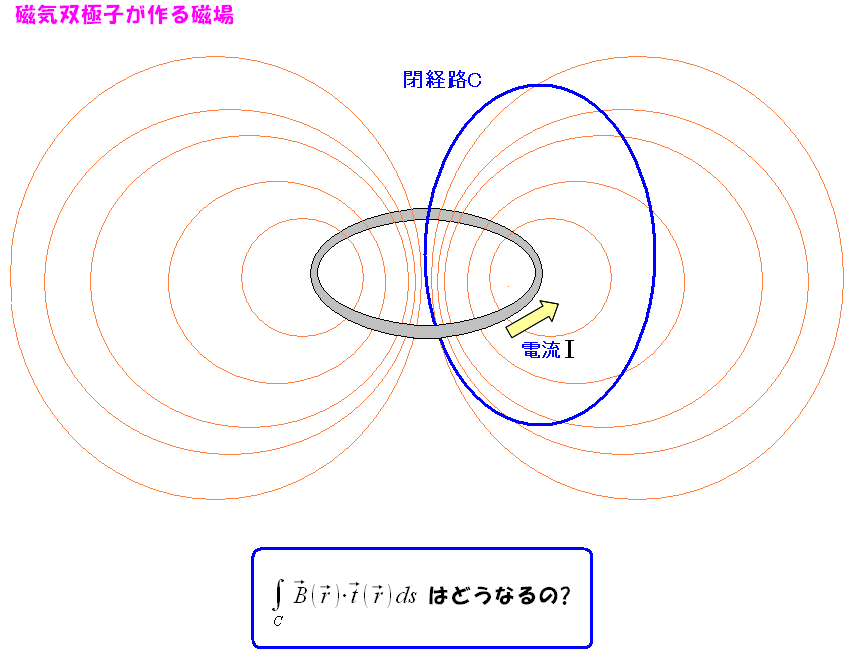 |
| この場合、どう考えれば良いのか。 |
これがまさに・・・
アンペールの法則
なのだ。
無限に長い導線があり、その周囲を反時計周りで1周させる際
各地点での磁束密度の足し合わせは、いかなる経路でも
透磁率(μo)と電流(I)の積になるのだ。
| 経路が違えど、経路積分の値は電流のみに依存する |
|---|
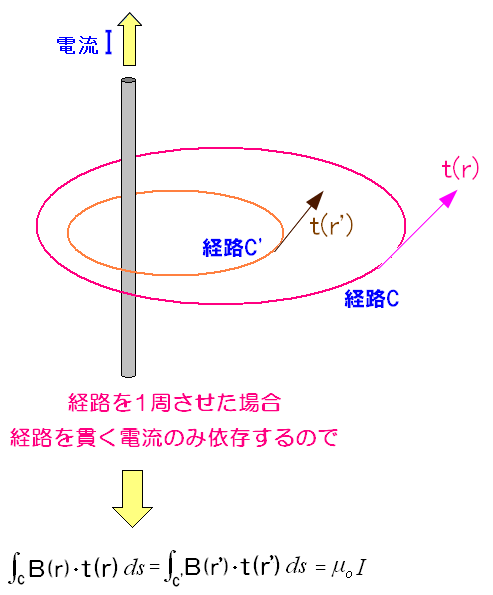 |
|
閉経路を貫く導線を流れる電流によって、経路積分の値が決まるため 閉経路の形状は関係ないというのだ。 それがアンペールの法則なのだ。 |
20世紀、電磁気を習った時は ふ〜ん、そうなの という感じで、何も疑問に感じずにいたのだが 今回は、電磁気の説明を書く立場になったため 論理の飛躍があったりすると、そこから先に進めず なんでやねん??? なのだ。 そこで数値計算で確かめてみる事にした。
| 数値計算で、電流のみに依存する事を示してみる |
|---|
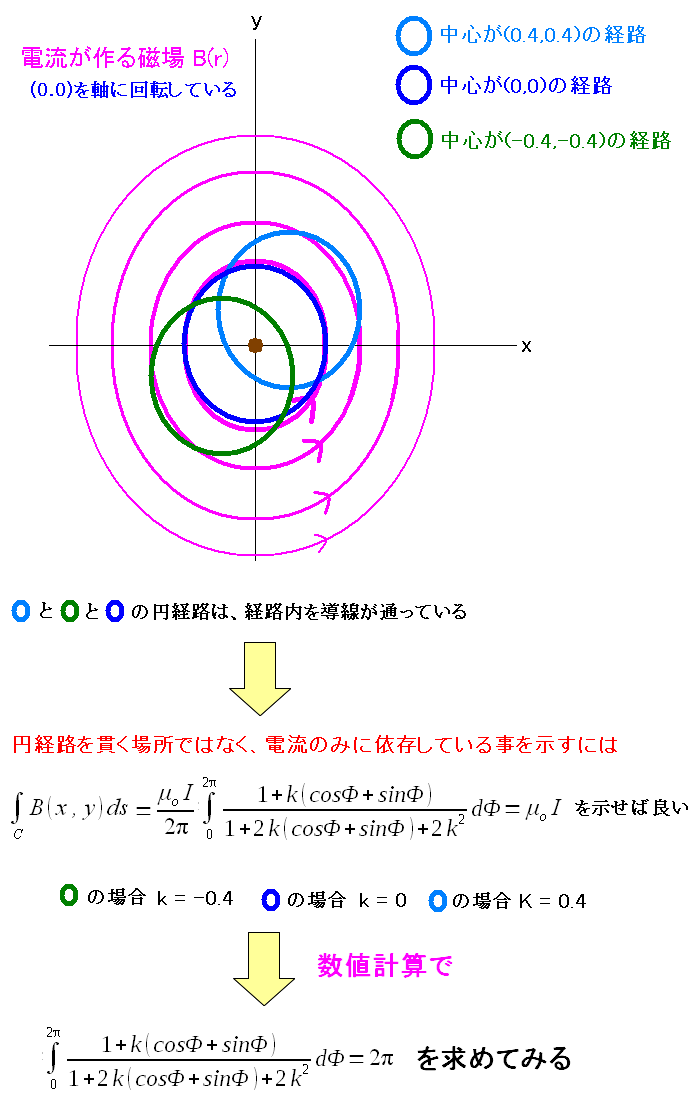 |
| 計算する閉経路は、全て導線のある(0,0)を、またぐようにしている。 |
さきほどのプログラムを使って数値計算を行なってみる。
| 数値計算のプログラム |
|---|
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int main(void)
{
double fai , k , pi , pi2 , delta , dfai ;
double total ;
pi = 3.1415926 ;
pi2 = pi*2.0 ;
k = 0.4 ; /* ここの数値を変える */
dfai = 0.00001 ;
total = 0.0 ;
for ( fai = 0.0 ; fai < pi2 ; fai += dfai )
{
delta = ( 1.0 + k * (cos(fai) + sin(fai) ) ) /
( 1.0 + 2.0 * k * (cos(fai) + sin(fai)) + 2.0 * k*k) ;
total += (delta * dfai);
}
printf("total = %lf \n",total);
return(0);
}
|
計算結果が出た。
| 数値計算の結果 | |
|---|---|
| k = -0.4 | 6.283191 |
| k = 0.0 | 6.283190 |
| k = 0.4 | 6.283189 |
結果を見る限り、閉経路の積分の値は
電流のみに依存している
なのだ。
閉閉路の積分の値は、導線の電流のみに依存する事がわかった。
ところで閉経路の中を、以下の図のように、3本、導線が通っていて
電流が流れている場合は、それぞれの電流が作り出す磁場の合成で
考えれば良いというのだ。
| アンペールの法則とは |
|---|
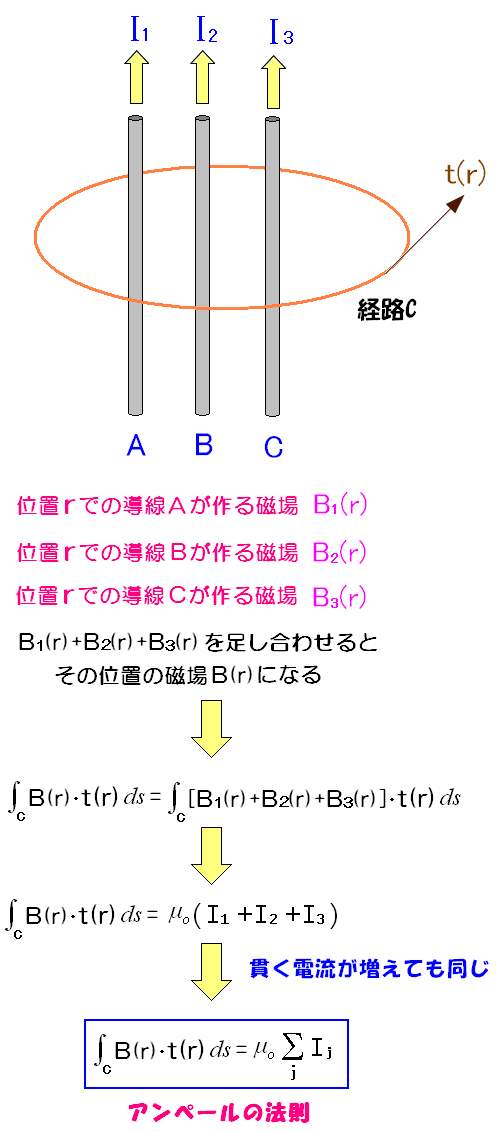 |
|
個々の導線に流れる電流が作る磁場の合計と、 閉経路を貫く電流の合計量との関係式だ。 この関係式をアンペールの法則と呼ぶ。 |
ようやくアンペールの法則のたどり着いた。
アンペールの法則の微分形
アンペールの法則の微分形。 微分系なので、微小領域で見た場合のアンペールの法則だ。 導線の断面で考えたら、わかりやすくなる。
| 導線の断面の微小領域を考えてみる |
|---|
 |
|
ガウスの法則の微分形と同様の方法で、電流密度と それが作り出す磁場との関係式を導き出すのだ。 |
ところで教科書では、いきなり
ストークスの定理より
という文言を入れて、あっさりと説明してしまう場合が多い。
| 教科書風に説明すると |
|---|
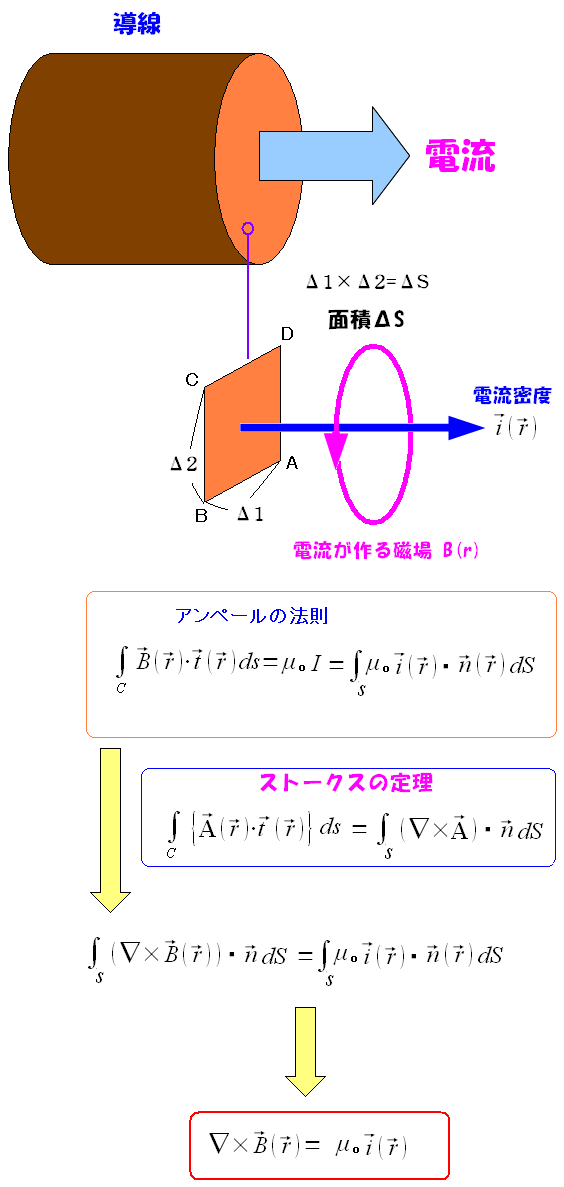 |
|
教科書では「ストークスの定理より」で、計算を省略する場合が多い。 でも、いきなりストークスの定理と言われても、納得しにくい部分がある。 バカ丁寧に、ガウスの法則と同じように、微小区間の説明をした方が 納得しやすいのはある。私は、そういう方法を採用した。 |
電磁気学入門の目次
| 電磁気学入門:目次 | |
|---|---|
| スカラーとベクトル | 簡単なスカラーとベクトルの話です。 ベクトルは方向と大きさを持つ量。方向という量持っているだけに注意が必要です。 |
| 静電気の発見からクーロンの法則 | 今でこそ当たり前の静電気や導体、絶縁体、電荷など どういう経緯で発見し、クーロンの法則まで至ったのかの話です。 |
| クーロン力、電場、近接作用 | 4つの力のうち、クーロン力の位置づけ 電荷が作り出す作用の電場。近接作用の話です。 |
| 微分、全微分、方向微分 | 簡単な微分、全微分、方向微分の話です。 ここをしっかり押さえないと、電磁気の数式の意味が わからなくなります。 |
| ベクトル解析 |
電磁気に必要なベクトル解析の話です。 勾配(grad)、2次元のグリーン定理 ストークスの定理の話です。 |
| 電位ポテンシャル | 電位ポテンシャルです。勾配と電場の関係を使って説明しています。 |
| 電気双極子 |
電気双極子の話です。 物質中で起こる分極を理解するのに必要です。 |
| ガウスの法則 | ガウスの法則の積分形、微分形の話です。 |
| ポアソンの方程式、ラプラス方程式 |
ポアソンの方程式、ラプラス方程式の話です。 単に電荷分布から電位を求めるだけの話にとどまらない 奥が深い分野です。ポテンシャル論、デルタ関数 グリーン関数、固有値問題について触れています。 |
| 静電場と渦なしの法則 |
静電場で、電荷を1周させた時の仕事はゼロ 微分形と微分形の渦なしの法則の話です。 |
| ビオサバールの法則 |
電気と磁場の関係の発見の話から ビオ・サバールの法則が導かれるまでの話です。 |
| 磁気双極子 |
磁気双極子の話で、回転電流になります。 物質中の磁場の話にも関連します。 |
| アンペールの法則 |
アンペールの法則の話です。 積分形・微分形だけでなく、閉回路に流れる電流が作る 磁気双極子の話なども書いています。 |
| ローレンツ力 |
磁場中を移動する電荷にかかる力(ローレンツ力)の話です。 ローレンツ力は相対性理論が絡んでいる事も紹介しています。 |
| ファラデーの誘導起電力の法則 | ファラデーの誘導起電力の話です。 |
| うず電流を使った簡単な物理実験 | 電力計に使われるアラゴの円盤。 そしてIH調理器で熱するために発生させる、うず電流は レンツの法則から電流が発生する原理を応用した物だ。 アラゴの円盤の実験と、IH調理器を使った実験です。 気分転換で読んでください。 |
| ベクトルポテンシャル |
わかりにくいベクトルポテンシャルの話です。 電位は電荷が作る電気のポテンシャルだが ベクトルポテンシャルは電流が作る磁場のポテンシャルの話です。 |
| オームの法則の微分形 | 微小領域でのオームの法則の話です。 |
| マックスウェルの方程式 |
4つのマックスウェルの方程式を書いています。 電場と磁場の変化を図にする事で rotの回転の意味も理解できます。 |
| ゲージ変換 |
ゲージ(gauge)は物差しの意味です。 マックスウェルの方程式をE(電場)とB(磁場)の関係式から φ(電位ポテンシャル)とA(ベクトルポテンシャル)の関係式に 書き換える際、ゲージ変換が使われます。 ゲージ変換の役目を書きました。 |
| 電磁波 |
マックスウェルの方程式から電波が伝わる様子を 視覚的に見てみる話です。 |
| 回転のrotはベクトルの微分 |
ベクトル解析や渦なしの法則で出てくるrotは ベクトルの微分という話です。 |
| 電磁気学の単位系 | 電磁気学の単位系の話です。 物理量の単位系の指数を見る次元解析 電磁気学の歴史と単位系の変遷について触れました。 |
| 電気泥棒:電気と法律の話 |
電気は物体なのか、無形物なのか。 明治時代に、電気を無断で使った場合、物か、そうでないかで 窃盗罪になるかどうかが裁判で問われました。 ちょっとした科学と法律の話です。気分転換で読んでください。 |
| 数ベクトルと基底ベクトル | ベクトルの話です。 矢印だけがベクトルでない事。 数ベクトルと基底ベクトルの違いの話です。 多様体、反変・共変ベクトルを理解するのに必要です |
| 多様体 | 空間を一般化した話です。 ▽(ナブラ)の正体に迫まります |
| 外積代数 |
外積、テンソルについて書いています。 極性ベクトル、軸性ベクトル 外積は行列で、ベクトルは見せかけの姿だった話です。 |
| ベクトルの双対関係 |
反変ベクトル、共変ベクトル、双対関係 ベクトル解析、外積代数の話 外積、テンソルについて書いています。 |
| ローレンツ力と相対性理論 |
磁場は電場の相対論的効果だった話です。 ローレンツ力を使って、導線が作る磁場を使って説明です。 |
| 微分形式 |
多様体の話の続きです。 座標に依存しない形での関数やベクトルの微分の話です。 ガウスの法則、アンペールの法則、マックスウェルの方程式が 鮮やかな形で表現できます。 ∇(ナブラ)の正体もわかります。 |
| 物理と対称性 |
マックスウェルの方程式をよく見ると対称性があります。 物理の方程式と対称性を数学的な観点でみると 意外なつながりがあるという話です。 |
| マックスウェルの応力 |
電気力線を弾性体(ゴム)とみなして、力の伝わり方などを 説明した考え方です。 |
| 電場エネルギー | 電場が持つエネルギーの式を導いた話です。 |
| 磁場エネルギー |
磁場が持つエネルギーの式です。 手抜きの説明と、直流RL回路を使った説明を書きました。 |
| ポインティングベクトル |
電磁エネルギーの流れ「ポインティングベクトル」の話です。 電磁波でもエネルギー保存則が成り立つ話から ポインティングベクトルを導いています。 |
| 電気エネルギーは導線の外を伝わる |
導線の外を電気エネルギーが流れる話です。 私が誤解した事、その誤解を解いていく過程を紹介しながら 「目からウロコ」にたどり着いた話です。 |
| 物質中の電場 | 物質中の電場の話です。 分極の話をしながら、物質中の電場の話をします |
| 物質中の磁場 | 磁性の話をしながら、物質中の磁場の話をします |
| 物質中のマックスウェルの方程式 | 物質中でもマックスウェルの方程式が成り立つ話です。 |
| 導体に侵入する電磁波 |
導体に侵入する電磁波が減衰していく話です。 表皮効果と同じ「表皮の厚さ」が出てきます |
| 表皮効果 |
目的の表皮効果の話です。 マックスウェルの方程式を解きながら 交流電流の周波数を上げると、表面にしか電流が流れなくなる話です。 |