システム奮闘記：その105

ポアソンの方程式



Tweet 

(2016年5月22日に掲載)



電荷と電位の微分方程式


　荷電粒子と電場との関係式はガウスの法則だった。
　荷電粒子と、それが作り出す電位との関係式がある。
　それがポアソンの方程式だ。

　導いてみる事にする。
ポアソンの方程式
ポアソンの方程式
ガウスの微分形と、電場と電位の関係式から導ける。 

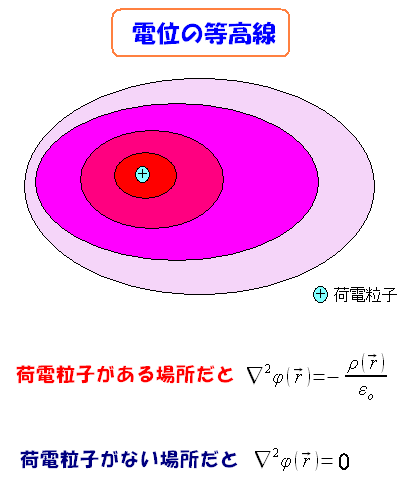
　荷電粒子が作る電位の等高線を描いてみる。
荷電粒子が作る電位の等高線
電位で荷電粒子と関係
荷電粒子が作り出す電位の等高線を描いてみた。
ポアソンの方程式は、電位から荷電粒子の有無や
荷電密度がわかるのだ。 

　ふと気づいた。

　ポアソンの方程式も、点で見てるやん!

　まさに微分形なのだ。




ポアソンの方程式を使って電位を求める


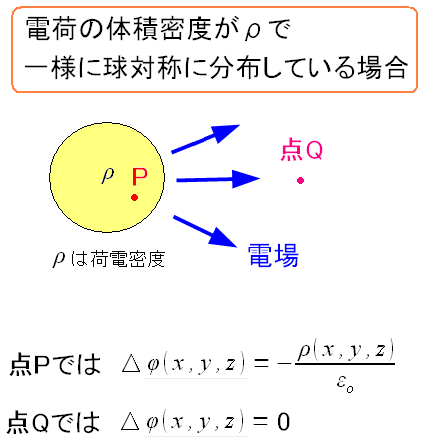
　ポアソン方程式だが、よく出てくる話として
真空中に電荷を帯びた球体が作る電位の話がある。
真空中に置かれた電気を帯びた球体上の雲を考える
真空中に置かれた電気を帯びた球体上の雲を考える
ふわっとした雲みたいな感じで、電荷の体積密度がρの
球対称の領域があるとする。(導体ではない!!)

この時、鉄球を中心を座標の原点と考えた場合
それぞれの位置での電位と荷電密度の関係式は
ポアソンの方程式で表せる。 

　あくまでも体積密度ρの球状の雲

　なのだ。
　ここまで念押しするのには訳がある。

　導体だと、この話は成り立たへんから

　なのだ。
電荷を帯びた導体だと、電荷は表面にしか存在しない
ふわっとした雲みたいな感じを強調したのは
導体の場合だと、電荷は表面にしか分布しないのだ。

正直な事を書くと、最初は「導体」としてポアソンの方程式の話を書いたが
だいぶ後にでてきたマックスウェルの応力の部分で
電荷を帯びた導体の場合、表面にしか電荷が分布しないのを知って
絵や文章を書きなおしたのだ。

もちろん、導体の場合、表面にしか電荷が分布しない理由は
マックスウェルの応力の部分で登場します。 

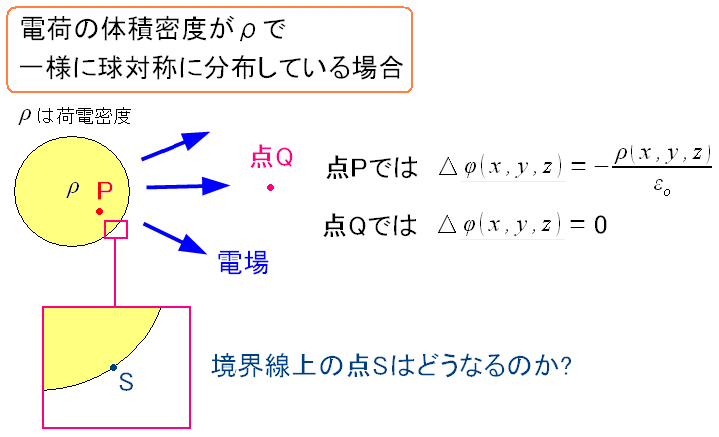
　ところで電荷の雲の内側と外側では、ポアソンの方程式は異なるのだが

　境界線上では電位が同じ

　になるはず。
境界線上での電位について
境界線上での電位について
電荷の雲の内側と外側との境界線上は、電位は同じであるはず。
この当たり前の事が、ポアソンの方程式を解く上で重要になる。 

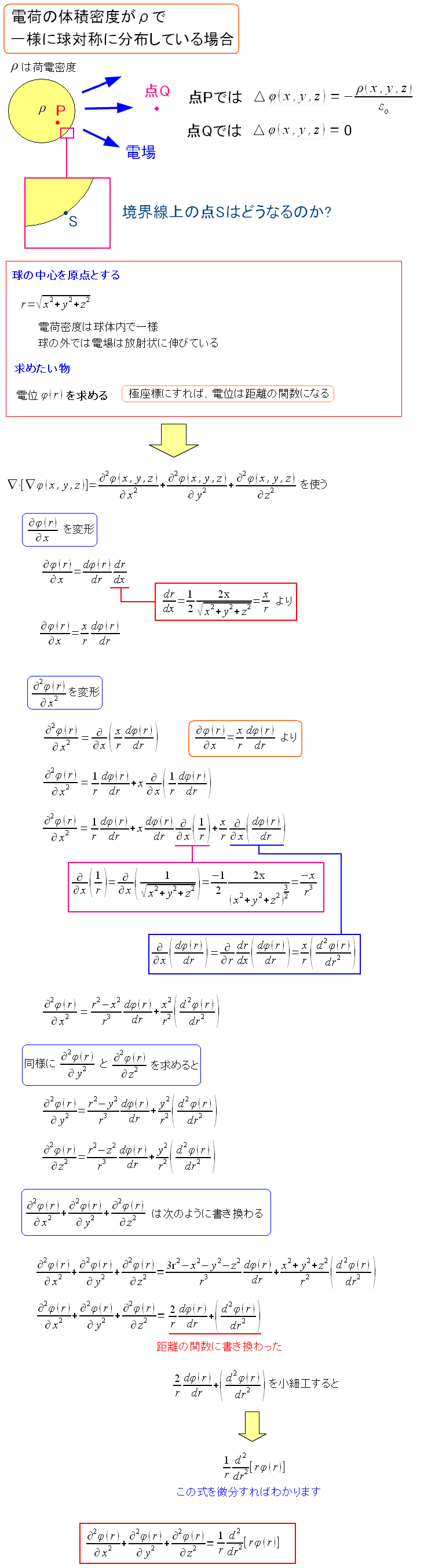
　そこで電位を求めるため、以下の準備を行なう。
電荷の雲の中と、その周辺に関する条件設定
導体とその周辺に関する条件設定
球体状の電荷の雲の中心を原点とする。
球は全方位に対して対象なので、極座標で考える。
ラプラシアンを極座標に変換した後、微分方程式を解く事になる。 

　ポアソンの方程式を極座標での表現に変換したので
ここから微分方程式を解く作業になる。
微分方程式を解く
微分方程式を解く作業
球体状の電荷の雲の中心(座標の原点)を含めて電位は連続。
電荷の雲の外側の場合、無限に遠い場所だと電位はゼロになる。
あとは境界線上では、電位は同じである事。
そして電位の関数が連続である事(傾きを表す導関数の値が同じ)

これらの条件を考慮すると、電位を表す方程式が解けるのだ。 




ポアソンの方程式と境界値問題


　ところで静電場中に導体を置いた場合、導体の周囲の電位は
どうなるのかの話がある。これもよく出てくる。
静電場中に導体を置いた場合の周囲の電位は
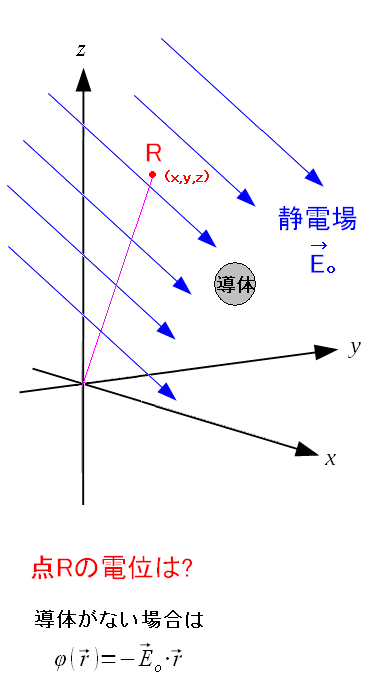静電場中に導体を置いた場合の周囲の電位
静電場中に導体を置いた時、点Rの位置での電位はどうなるのか?
導体がない場合だと、上図に書いている式の通り、電位はわかるのだが・・・。 

　ところで静電場中に導体を置いた場合、以下の現象が起こる。
分極が起こる
分極が起こる
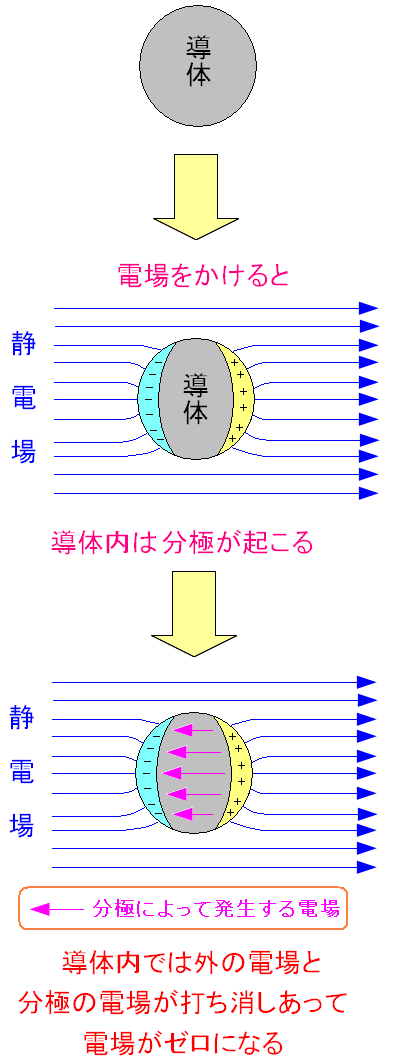静電場中に導体を置くと、導体内の自由電子が移動し分極が起こる。
導体内で分極が起こり、外からの電場を打ち消す状態になる。 

　導体内で分極が起こるため、静電場中に導体を置くと、
周辺の電位を求めるが容易ではなくなる。
導体を電気双極子と考える
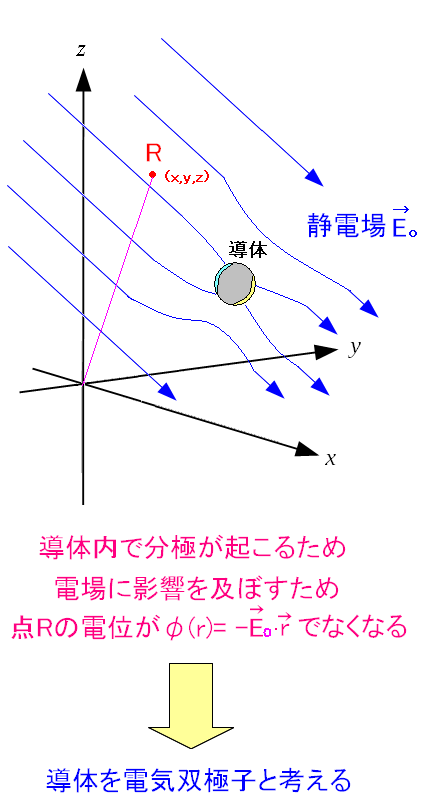導体を電気双極子と考える
電場によって導体が電気双極子になったため
その電気双極子から発生する電場の影響で
周囲の空間の電場が変わってしまうのだ。 

　電場によって導体が電気双極子になってしまった。
　この時、周囲の電位を求める際、どこの電位を基準にするかが問題になる。
境界値問題
境界値問題
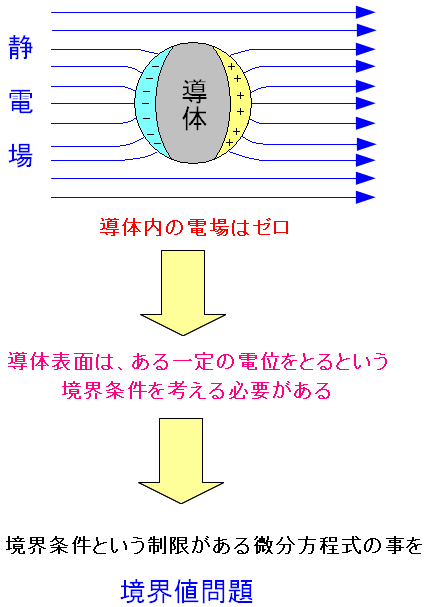電位の値そのものはわからない。
だが、導体内部では電位は同じだというのは
わかっている。
そこで導体内部を基準として周囲の電位を求めるのだ。
導体表面(導体と空間の境界)を決めて
電気を求める手法を、境界値問題というのだ。 

　実際に導体周囲の電位を求めてみる。
導体周囲の電位を求めてみる
導体周囲の電位を求めてみる
電位とは、どこかを基準にしているため
ここでは、導体内部の電位をゼロ(基準)にした。
すると、電位が求まったのだ。 





ラプラス方程式と調和関数



　正直な事を書くとポアソンの方程式の話だけを書いて
終わらせようと思ったのだが、少し踏み込んで調べてみると

　重要な話だらけやん!!

　しかも・・・

　知らへん話ばかりやん!!

　なので、踏み込んでいく事にした。
何が重要なのか
ポアソンの方程式から、ラプラス方程式と調和関数の話が出てくる
そこから芋づる式に、デルタ関数、グリーン関数、ポテンシャル論など
工学や量子力学などで使われる大事な関数の話になっていく事がわかった。 
　

　つまり、学生時代、ラプラシアンが出てくる微分方程式の問題の重要性を

　全く理解してへんかったのが露呈した

　のだ。

　でも、気にしない。
　20年前の話なので・・・

　笑い話になるのだ!

　忍法「開きなおりの術」を使った所で、話を前に進める。

　以下の資料を読む事にした。

　ディラックのデルタ関数
　グリーン関数
　ポアソン方程式とグリーン関数
　ディラックのデルタ関数 δ(x)PDF(奈良女子大)
　対話・グリーン関数(1)(PDF)
　電磁気学2講義ノート東京理科大学理学部物理学科(PDF)


　さてさてラプラス方程式を見てみる事にした。
　そこには調和関数という物が出てくる。
ラプラス方程式と調和関数
ラプラス方程式と調和関数
関数にラプラシアンを作用させてゼロになる方程式が
ラプラス方程式といい、それを満たす関数を調和関数というのだ。 

　調和関数が物理と関連するのだ。
　その具体例が

　ポテンシャル関数は調和関数の一種

　なのだ。

　電位ポテンシャルの式

　力学で習った重力ポテンシャルの式

　といったポテンシャルを表わす数式(関数)は

　調和関数

　なのだ。
実は後になって知ったのだが・・・
いかにも偉そうに「ポテンシャル関数は、調和関数の一種」と書いたが
実際の所、ラプラス方程式を追いかけている間にわかったのだ。
単なる私の嗅覚で、この話は重要かなぁと思い、調べていって
ようやく知ったのだ。

でも、これから電磁気を勉強しようと考えている人達には
最初の所で「こんな重要な話になる」と書いておいた方が
何をしようとしているのかが、わかるし、勉強する目的もわかるからだ。 


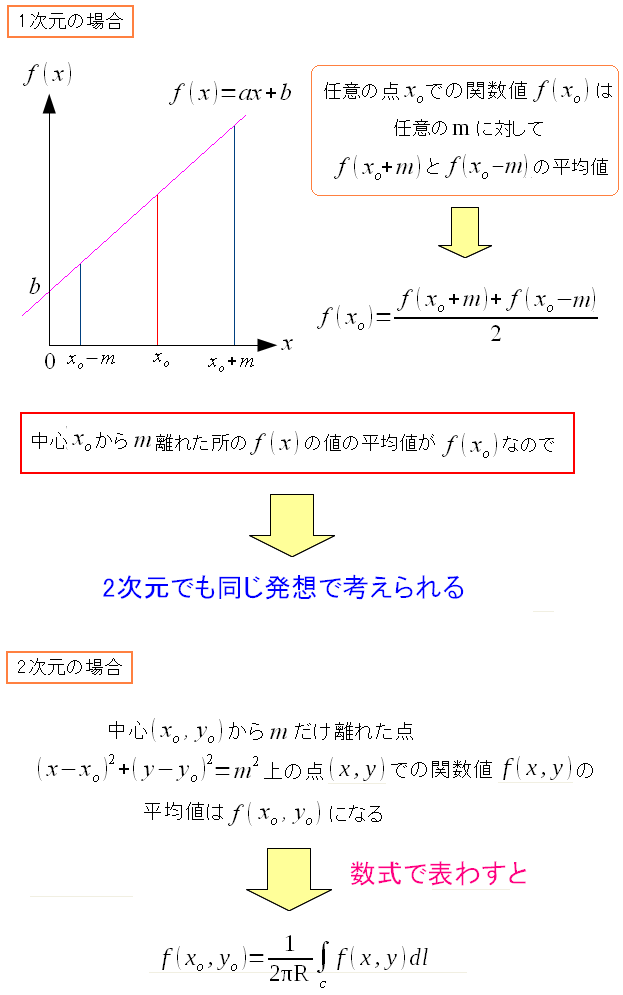
　調和関数が、どんな関数なのか。
　わかりやすく、1次元の調和関数を考えて見た。
1次元の調和関数
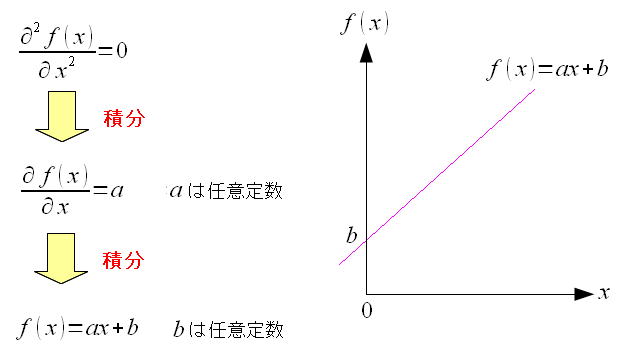1次元の調和関数
綺麗な直線になっている。 

　直線なので、以下の事が成り立つ。
調和関数と平均値の関係
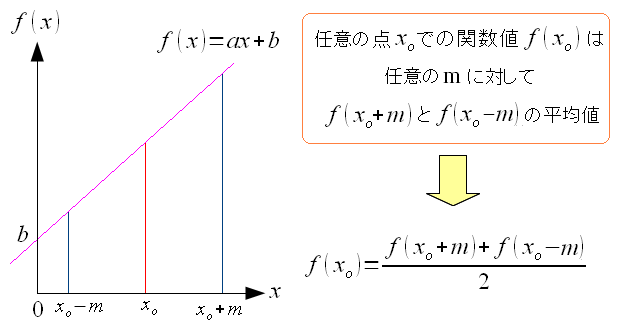調和関数と平均値の関係
1次元の調和関数で見ると、視覚でわかるため
当たり前のような話だが、2次元、3次元になると
直観的には、見た目では、わからなくなるだけに、重要になってくる。 

　平たく言えば

　中心から等距離にある値の平均をとれば

　中心の値になる

　というのだ。
　これが調和関数の性質の1つなのだ。

　だが、これだけだと

　だから何やねん!!

　になる。

　でも、ここで立ち止まらず、2次元の調和関数を見てみる。
2次元の調和関数。鞍(くら)型
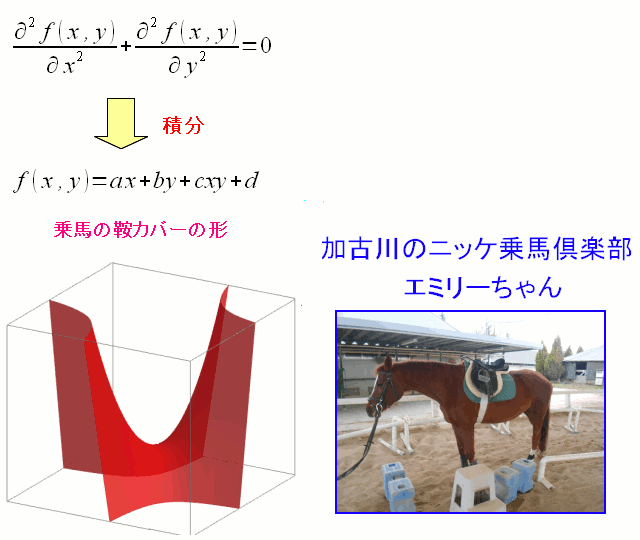2次元の調和関数。鞍(くら)型
2次元の調和関数の中の1つに鞍(くら)型がある。
乗馬の鞍(くら)を連想するのだ。

(余談)
乗馬。2015年に加古川で体験した。乗ったのはメスのエミリーちゃん。
黒田官兵衛の奥さん・光姫は加古川出身なので
「私の光姫ちゃん」と思いつつ、でも、乗馬をするには金がかかるので、
乗馬体験だけでやめたのだ。
日本毛織株式会社(通称・ニッケ)の工場が加古川にあったが
今は工場はないが、スポーツ施設や商業施設を運営していたりする。
もしかして工場敷地の跡地かも。 

　2次元の調和関数は、鞍型だけではない。
色々ある2次元の調和関数
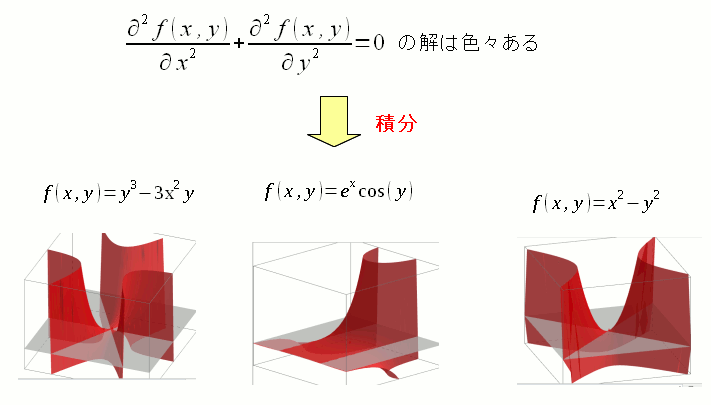色々ある2次元の調和関数
2次元になると、調和関数の数が増える。
ここに載せているのは、一部のみです。 

　1次元の調和関数と同様、2次元の調和関数でも
中心から等距離のある位置の平均値は、中心値と一致するのだ。
2次元調和関数と平均値
2次元調和関数と平均値
これも中心から等距離のある位置の平均値は中心値と一致する。

1次元の場合、等距離の位置は2ヶ所だったが
2次元の場合は、線になったので、合計するには積分するしかないのだ。 

　中心から等距離にある位置と調和関数の値、その平均値を
図にしてみた。
2次元調和関数と平均値を図にしてみた
2次元調和関数と平均値を図にしてみた
2次元なので、図にして説明ができるのだ。
ただ、計算となれば、面倒になってくる。 

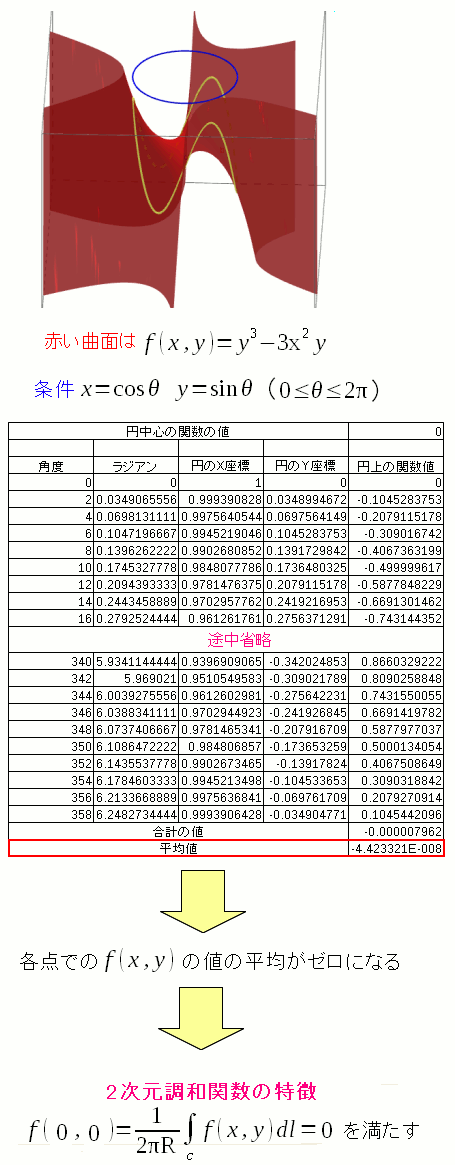
　綺麗に積分ができなくても

　数値計算すればエエやん!!

　というわけで、中心から等距離にある点を等間隔に取り出し
それの平均値を求めたみたのだ。
中心から等距離にある点を等間隔に取り出し、平均値の計算
中心から等距離にある点を等間隔に取り出し、平均値の計算
こういう時、案外、LibreOfficeのcalcやエクセルが便利だったりする。
中心の値はゼロなので、等距離にある点の数値の平均値がゼロになれば良い。
見事に近似値がゼロになったのだ。 

　ところで調和関数は、ラプラシアンを作用させるとゼロになる関数だ。
　ラプラス方程式がゼロになるという事だ。
　実は、ゼロになる事の重要なのだ。

　ポテンシャル関数は調和関数の一種

　なのを思い出して、ラプラス方程式がゼロ以外の値をとると
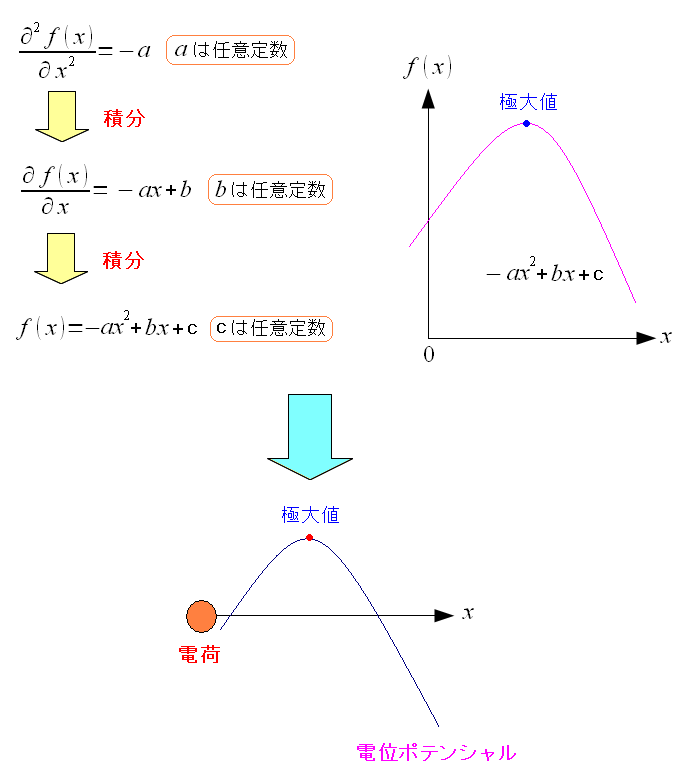
以下のような、おかしな事が起こってしまうのだ。
もし、ラプラス方程式がゼロでない場合
もし、ラプラス方程式がゼロでない場合
1次元(距離)で見るとわかりやすい。
重力ポテンシャル、電位ポテンシャルで説明する。

重力の源の質点、電位・電場の源の電荷。
源がある所が、ポテンシャルの最大・最小になる。

もし、ラプラス方程式がゼロでない場合、質点や電荷のない場所で
ポテンシャル関数が極小値(極大値)を持つ事になる。

極小値や極大値にポテンシャルを生み出す物が存在していまう事になり
矛盾してしまうため、極小値(極大値)を持たないよう
ポテンシャル関数(調和関数)は、ラプラス方程式では常に0になるのだ。 


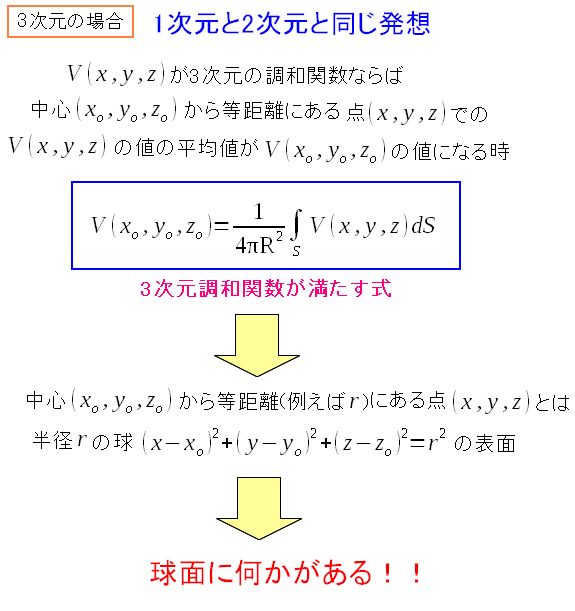
　さて、3次元の調和関数だが、図にできないし、計算する気も起こらないので
数式だけ書いておく。
3次元調和関数と平均値
3次元調和関数と平均値
球面の値の平均値が、中心の値と同じという。
球面。物理で色々、出てきそうだ。 

　球面で何かがあるとすると、球面の状態を知りたくなる。
　この時、出てくるのが

　球面調和関数

　なのだ。

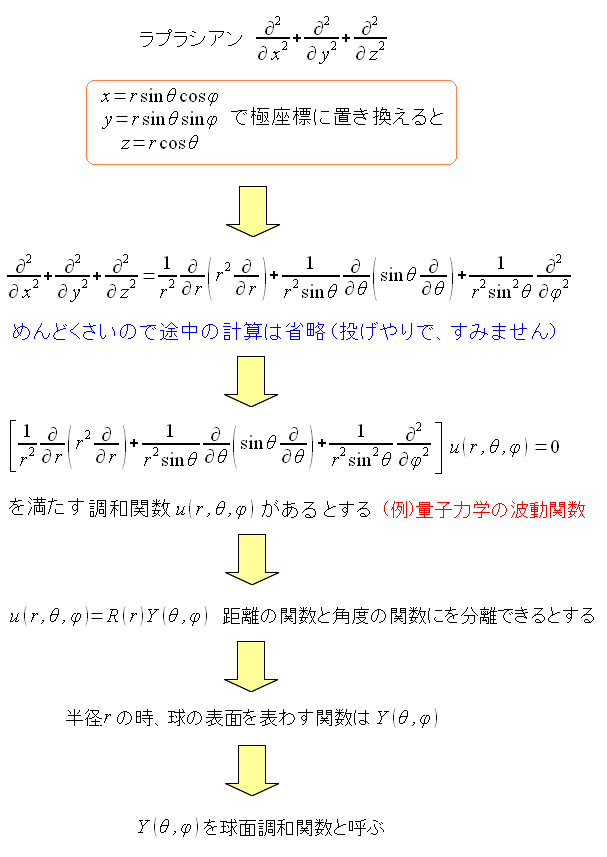
　調和関数を直交座標系から極座標系にして
距離の関数と角度の関数を分離させ
角度の部分だけを取り出した物を、球面調和関数という。
球面調和関数
球面調和関数
ラプラシアンを極座標系に書き換える。
距離と角度の関数が独立している場合
角度の部分(半径rの位置)の調和関数が求められる。

量子力学で中心の質量mの原子が作るポテンシャル関数から
角度だけに依存する球面調和関数部分を取り出して
電子の軌道の状態を知るなどに使われるようだ。 

　量子力学について軽く触れてみたいのだが・・・

　量子力学は、わからへん

　なのだ。薄っぺらいメッキをしても、すぐに剥がれるだけなので
これ以上、先には進まない事にする。


　ちなみに球面調和関数を踏み込むと、直交多項式の

　ル・ジャンドル多項式

　が導けるのだ。

　でも、これも飛ばすことにする。


　ところでラプラス方程式や調和関数の数学的構造を調べる分野の事を

　ポテンシャル論

　という。

　そんな分野があったとは全然知らなかったのだ。　




デルタ関数とグリーン関数


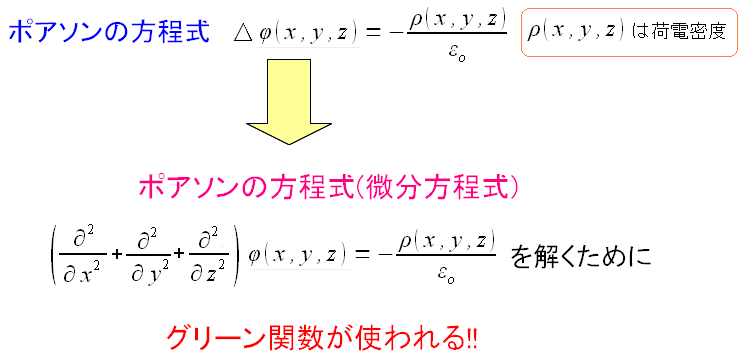
　ポアソンの方程式を踏み込んでいくと、デルタ関数やグリーン関数にたどり着く。

　話が長くなると退屈になるので、先に何をしようとしているのかを書く事にする。
　デルタ関数やグリーン関数の説明をしながら、デルタ関数によって
点電荷が作る電場の式が導けるというのだ。


　まずはポアソンの方程式を解くためにグリーン関数が使われる話を書く。
ポアソンの方程式
ポアソンの方程式
ポアソンの方程式という微分方程式を解くには
デルタ関数が出てくるし、そのデルタ関数を使って
求めたい関数(電位)を知るには、グリーン関数を避けて通る事はできない。 

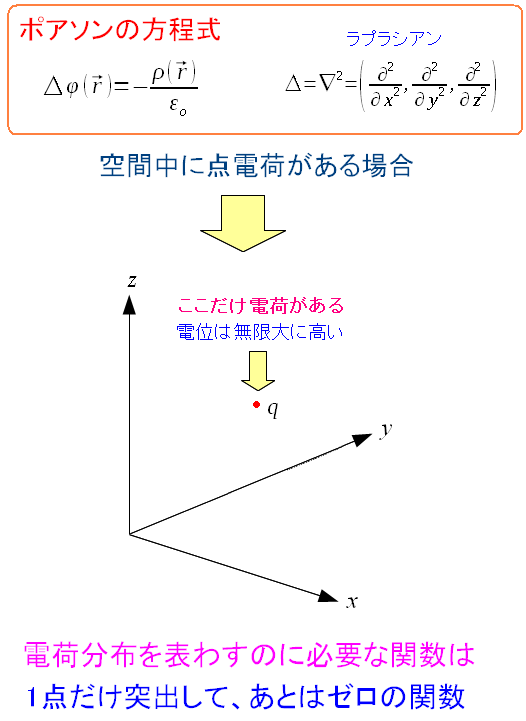
　ところで点電荷の状態を見てみる事にする。
　電荷密度を考えると、以下のことに気づく。
点電荷の電荷密度について
点電荷の電荷密度について
点電荷の部分だけ、電荷密度が無限大になる。
密度を表現するには、1点だけ無限大になり
その他の領域ではゼロになる関数が必要になる。 

　1点だけ無限で、あとはゼロになるという関数の話。
　そんな事・・・

　全く気づかへんかった!!

　学生時代も、この記事の編集している当初も気づかなかったが
ポアソン分布の話を調べている時に、資料に書いてあったのを見て
初めて知ったのだ。

　私は、物理・数学には、全く向いていない事を痛感する。


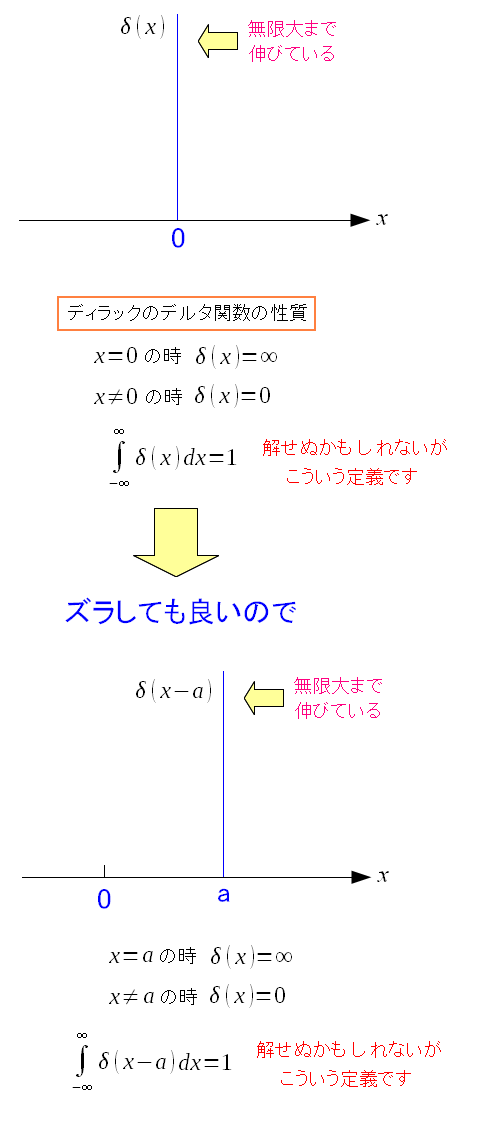
　ところで、1点だけ無限で、あとはゼロになる関数。
　ディラックのデルタ関数というものだ。
ディラックのデルタ関数
ディラックのデルタ関数
1点だけ無限大になり、あとはゼロ。
そして平均値は1になるという関数なのだ。

ディラックは物理学者で、量子力学の研究の際
デルタ関数を考えついたのだ。

1点だけ無限大で、無限の直線上の数字の並び(‥0,0,0,∞,0,0,0‥)を
平均すると1になる。無限大を、数字の個数(∞個)で割ると1になる

いまいち、よくわからんだけに、解せない所はあるが
定義なので受け入れるしかないのだ。 

　デルタ関数を点電荷で使ってみる。
デルタ関数を点電荷で使ってみる
デルタ関数を点電荷で使ってみる
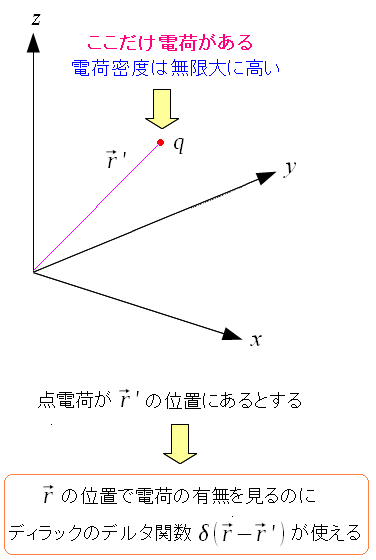rの位置での電荷の有無を表現するのにデルタ関数が使える。 

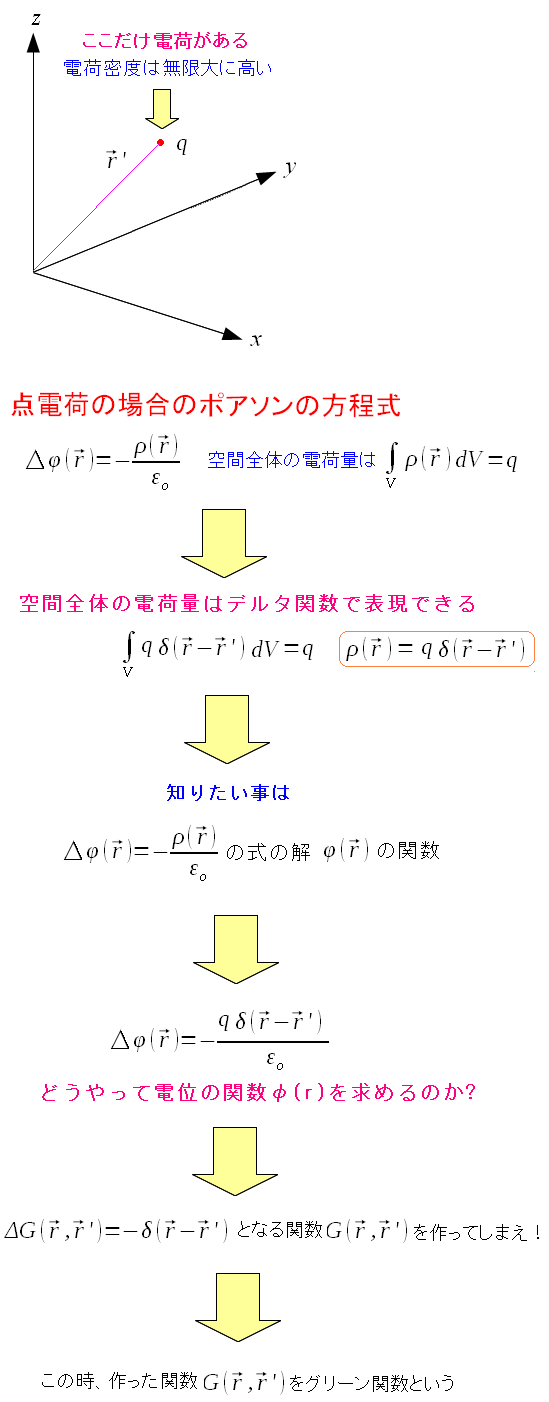
　そこで実際にデルタ関数を使って、空間における
点電荷の電荷密度を考えてみる事にする。
デルタ関数を使って、空間における点電荷の電荷密度を考えてみる
デルタ関数を使って、空間における点電荷の電荷密度を考えてみる
ポアソンの方程式にデルタ関数を使ってみる。
だが、問題は、デルタ関数を決めても
そのまま微分方程式を解いて、求めたい電位の関数φ(r)を
求めるのは困難だ

ラプラシアンを作用させてデルタ関数になるという関数を使い
上手に求めたい関数φ(r)を求めるのだ。
この際、ラプラシアンを作用させる関数をグリーン関数という。

後述しているが、グリーン関数は伝播関数と呼ばれ、応用物理や工学などに使われるのだ。 

　さて、グリーン関数を使ってみる。
グリーン関数を使ってポアソンの方程式を解いてみる
グリーン関数を使ってポアソンの方程式を解いてみる
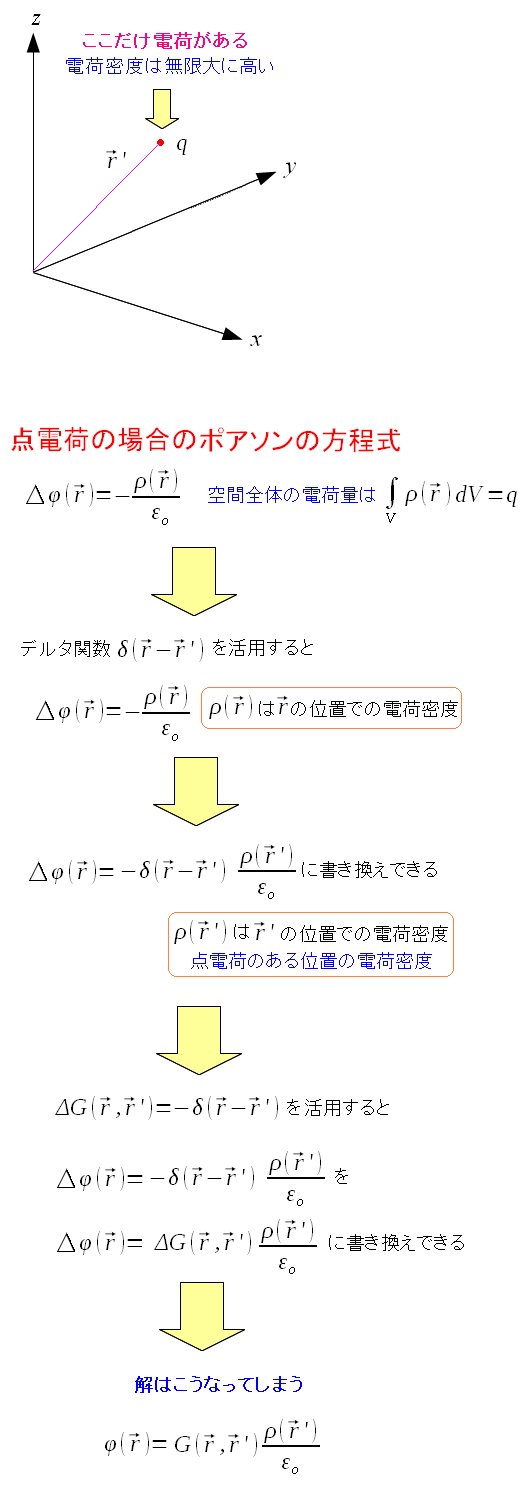グリーン関数の中身さえわかれば、あっけなく解ける感じがする。 

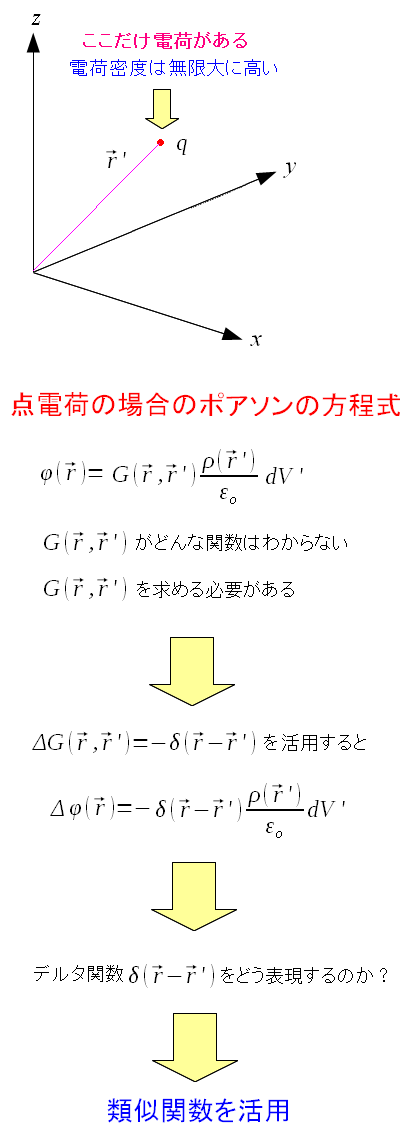
　グリーン関数を求めるには、元となるデルタ関数の中身を知らねばならない。
グリーン関数の中身がわからない
グリーン関数の中身がわからない
肝心のグリーン関数の中身を知らねばならないが
元となるデルタ関数の中身がわからないと
グリーン関数の中身もわからない。 

　そこでデルタ関数を作るのだ。
関数を作るという発想
デルタ関数の定義は決まっているが、中身は定義されていない。
そのため定義に合う関数を作る必要があるのだ。
私自身、デルタ関数の中身は何か調べていたが見つからなかった。
たどり着いたのは、個々の場合に合わせて
デルタ関数を作っているという事なのだ。 

　1点だけ無限大で、あとはゼロの関数。

　その1つが三角関数を使ったデルタ関数だ。
　1次元のデルタ関数を作ってみる。

　と書きつつ、資料の丸写しなのだ。
三角関数を使った1次元のデルタ関数の作り方
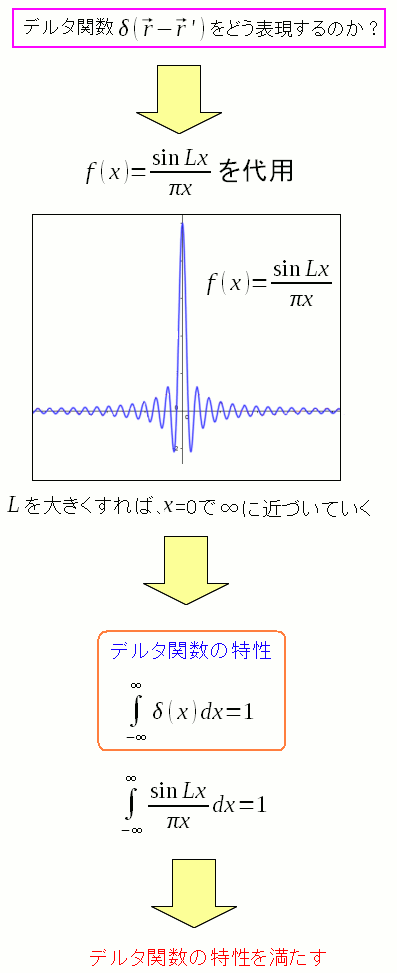三角関数を使った1次元のデルタ関数
代用関数を使ってデルタ関数を作るのだ。
これだとデルタ関数の特性の1つの
全領域を積分すると「1」になるを満たす。 

　このままでは使いにくいため、オイラーの公式を使って
三角関数を別の表現して、1次元のデルタ関数にしてみる。
1次元のデルタ関数
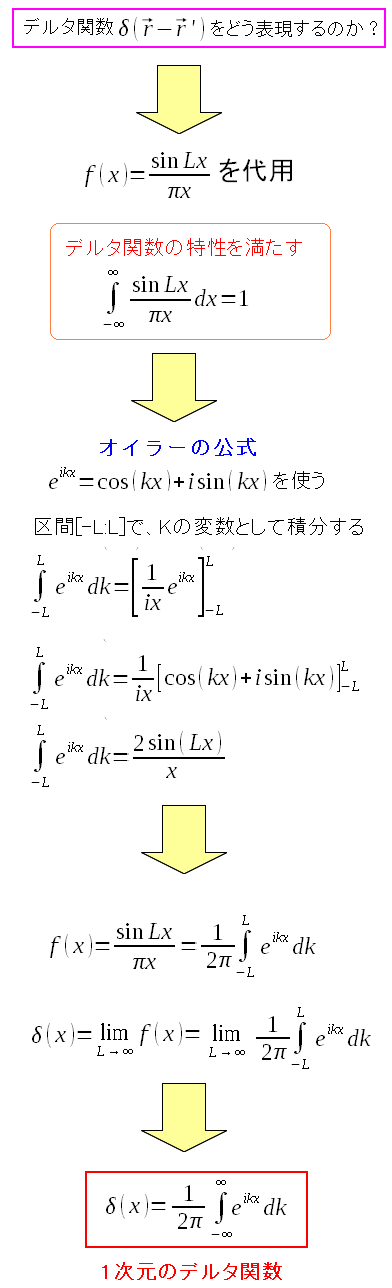1次元のデルタ関数
1次元のデルタ関数が出来上がった。
丸写しなのだが、楽ではない。理解するまでは大変だった。 

　楽ではない。でも、播州に行きまくっている私は「ラク」という。
ラクだけど、楽ではない!!
播州弁で「ラク」がある。意味は「大変」だ。
他の地域で、重たい荷物を持っている人に「ラクですか」と言うと怒られそうだ。

播州弁の「ラク」は、主に播州の西地域で使われている。
淡口醤油と揖保乃糸の龍野。(JRの表記の「竜野」はおかしい)
赤穂浪士や塩見饅頭の赤穂。Spring-8や赤松円心の上郡だ。
(実際に、地元の人に聞いてみたのだ)
だが、播州の東地域の明石、加古川辺りでは廃れているらしく、使われていない。 

　摂津人(私)による、播磨国(播州)の宣伝が終わった所で、閑話休題。


　3次元のデルタ関数を求める。
3次元のデルタ関数を求める
3次元のデルタ関数を求める
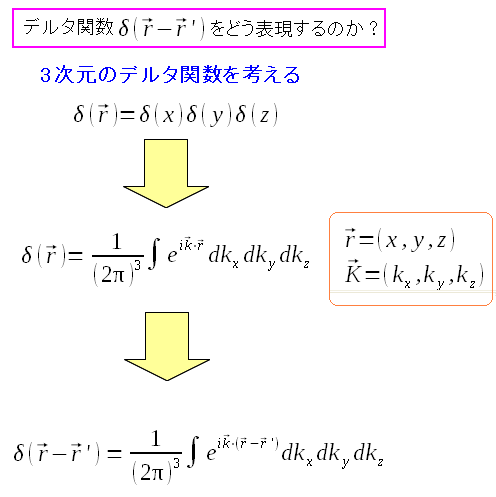単純に3方向のデルタ関数を掛け合わせるだけだ。 

　デルタ関数のできあがり!!

　なのだ。


　ふと気づいた。
　代用関数は、どっかで見た事がある!!
代用関数はパルス波をフーリエ展開した時の係数にあたる
代用関数はパルス波をフーリエ展開した時の係数にあたる
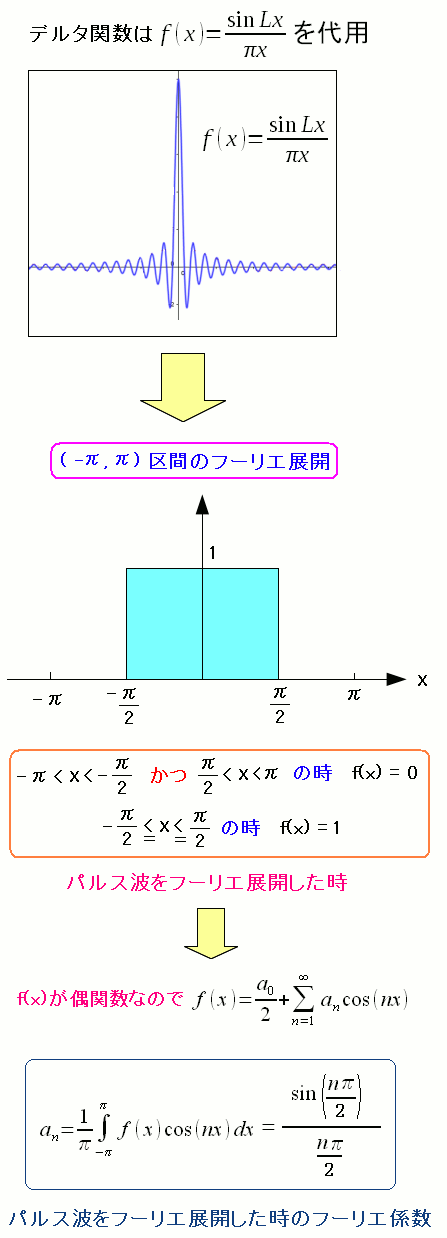パルス波をフーリエ展開した時に出てくる係数が、代用関数になっている。
確かにパルス波の幅を、無限に縮めるとデルタ関数になる。
パルス波のフーリエ展開については、「システム奮闘記:その104」
(無線LANの基礎　無線LAN入門)をご覧ください。 

　だが、今回知りたいポアソンの方程式を求めるのに

　三角関数で作ったデルタ関数は使わへん!!

　というのがわかった。
がっかりだけど無駄ではない
闇雲にデルタ関数の事を調べていたため
必要でなかったデルタ関数をみていたのだ。
でも、無駄ではない。三角関数を活用したデルタ関数は
量子力学で使われる。
それにパルス波をフーリエ展開した時の係数なのもわかった。
新しい事を知るための回り道というわけなのだ。 

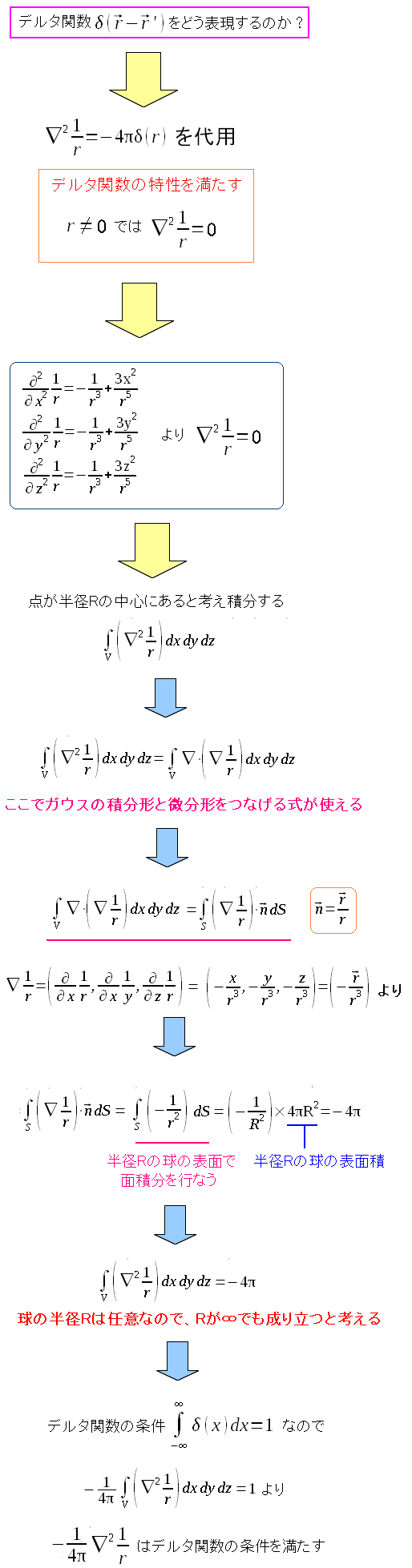
　さて、気を取り直して、実際に使うデルタ関数をみることにした。
ポアソンの方程式を解くのに使うデルタ関数
ポアソンの方程式を解くのに使うデルタ関数
言葉では表現しにくい関数だ。
デルタ関数が、ラプラシアンを作用させた関数になっている事で
後の展開であるグリーン関数を求めるのが楽になる。 

　使ってみると、簡単にグリーン関数と、求めたい電位の関数が求められる。
簡単にグリーン関数と、求めたい電位の関数が求められる
簡単にグリーン関数と、求めたい電位の関数が求められる
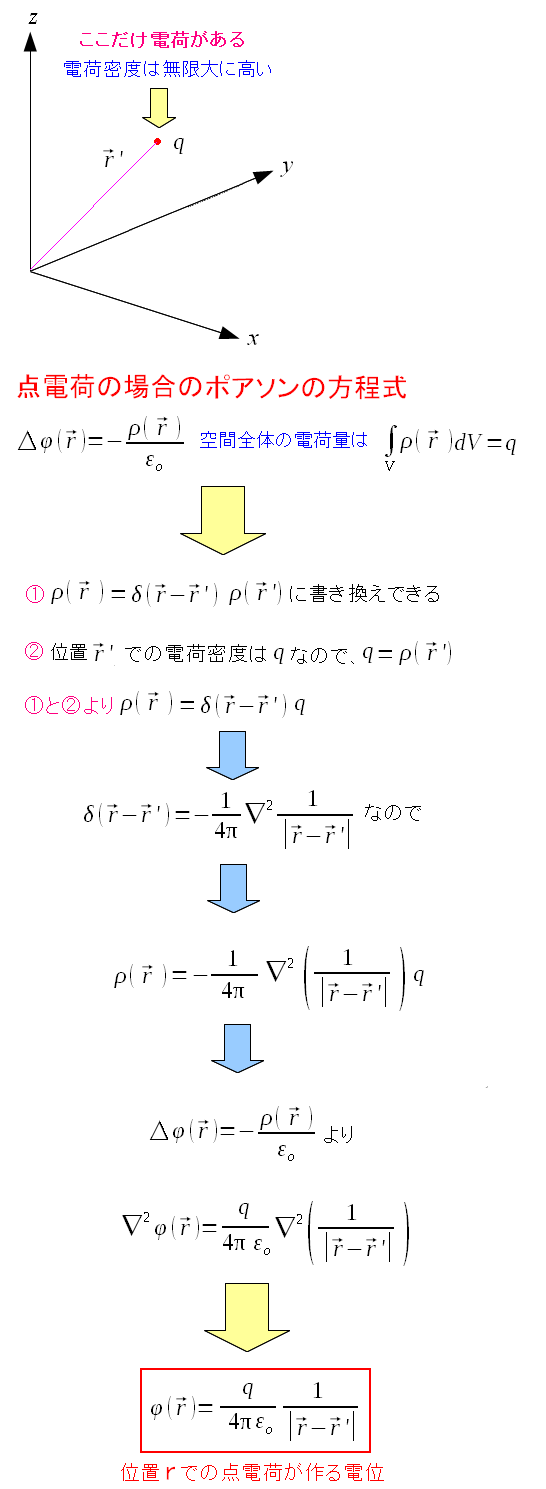あっけなく、求めたい電位の関数φ(r)が求まった。 

　デルタ関数とグリーン関数によって

　点電荷が作る電位が求められる

　を知った。

　物理法則の裏に隠れている数学の不思議さを感じてしまう。


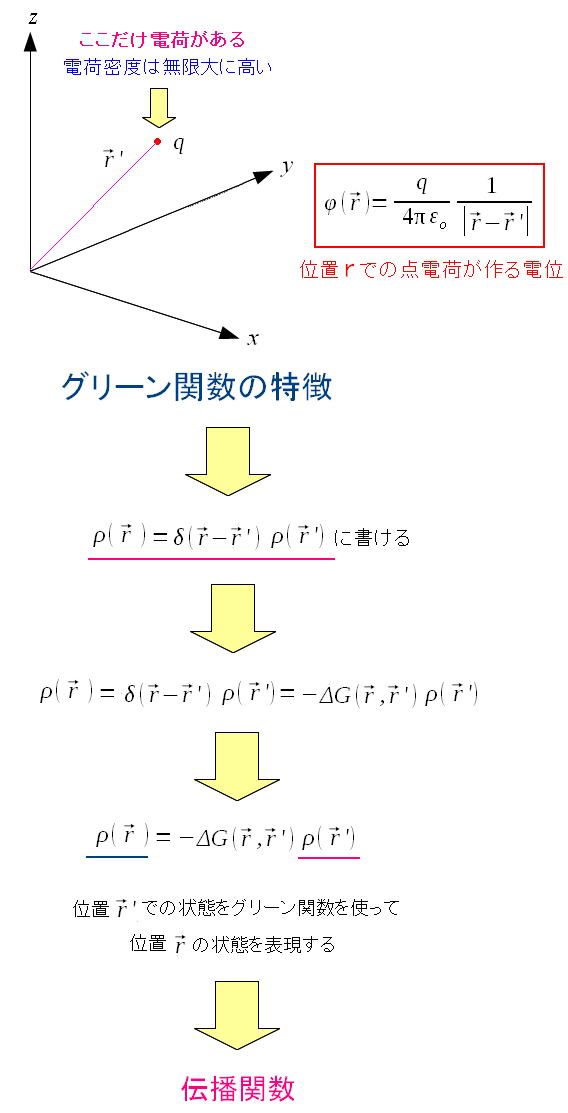
　ところでグリーン関数は何なのか?
　伝播関数と呼ばれる。その特徴を見てみる。
グリーン関数の特徴
グリーン関数の特徴
グリーン関数を使うと、rの位置からr'の位置の状態を知る事ができる。
rの電荷密度がわかれば、r'の位置の電荷密度がわかるのだ。

このように、グリーン関数を使えば、ある位置の状態から、別の位置の状態を知る事ができる
即ち、状態が伝播している感じなので、伝播関数と呼ばれるのだ。

温度分布や地震の伝播などに応用されているようだ。 

　グリーン関数の定義だが、以下のようになっている。
グリーン関数の定義
グリーン関数の定義
デルタ関数に似た性質なのだ。 




固有値問題


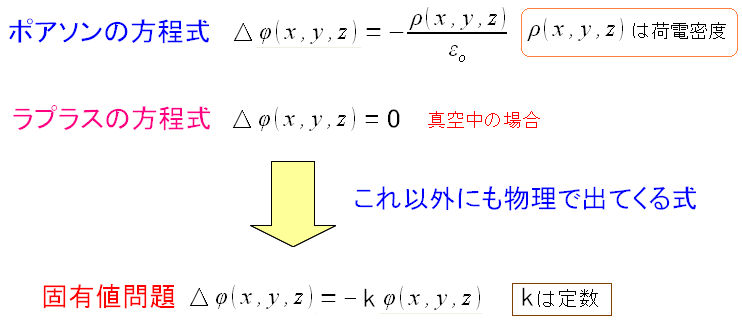
　ポアソンの方程式、ラプラス方程式の話が終わったので
ここで終わらせたいと思ったのだが・・・

　大事な基本話が抜けていた!!

　なのだ。

　学生時代はもちろん、これを書いている時も気づかなかったのだが
編集の終盤の段階で・・・

　知ってしまったのだ!!!

　知らなかった事を包み隠さず書くのがシステム奮闘記の基本方針。
　固有値問題にも触れる事にした。
微分方程式と固有値問題
微分方程式と固有値問題
微分方程式と固有値問題。
ある関数を2回微分すると、元の関数が出てくる問題がある。
式だけ見ると「なんじゃ」になるが、力学の最初に出てくる話だ。 

　高校物理で習う

　単振動の振り子の話

　なのだ。
単振動の振り子の話
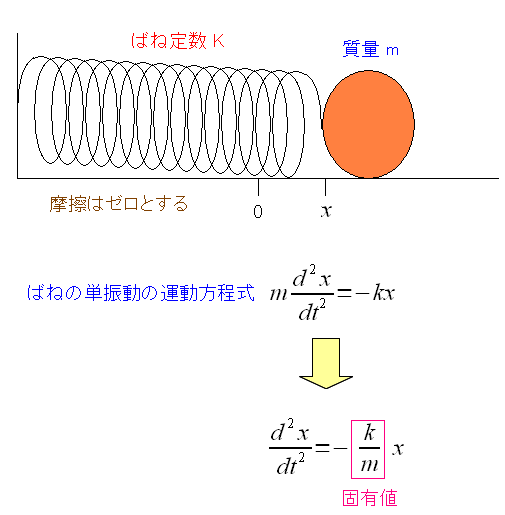単振動の振り子の話
単振動の振り子の話は高校の物理でも出てくる。
もちろん高校だと微分方程式は解かないのだが・・・

大学でも物理や工学系だと、1回生で習う力学の範囲だ。
だが、私は、この年齢になって、ようやく固有値問題だというのに気づいた。 

　そして微分方程式を解いてみる。
単振動の振り子の微分方程式を解いてみる
単振動の振り子の微分方程式を解いてみる
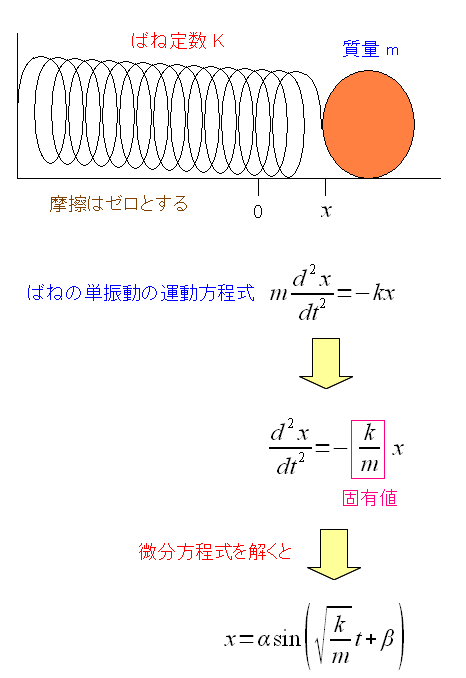この場合、簡単に微分方程式が解ける。 

　だが、摩擦を考えると微分方程式を解くのが難しくなる。
単振動の振り子の微分方程式(摩擦あり)
単振動の振り子の微分方程式(摩擦あり)
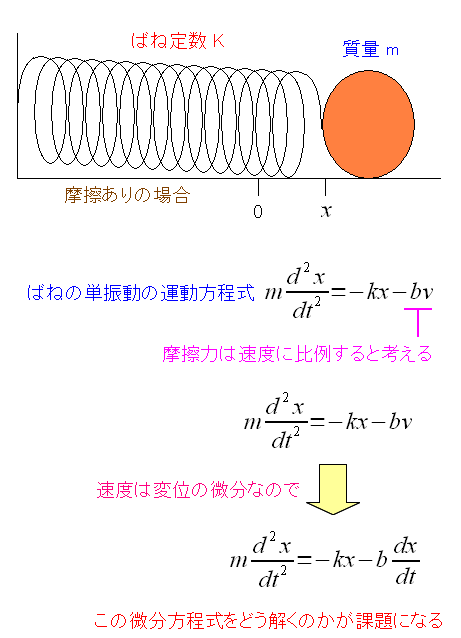摩擦があると、微分方程式の形が難しくなる。 

　今回は、微分方程式の話ではないので、この先は省略するのだ。

　固有値問題は、量子力学でも出てくるようだ。
　でも、ここでは量子力学の話はしないし、私が書けるだけの知識がないので
省略するのだ。



電磁気学入門の目次
電磁気学入門:目次
スカラーとベクトル 簡単なスカラーとベクトルの話です。
ベクトルは方向と大きさを持つ量。方向という量持っているだけに注意が必要です。
静電気の発見からクーロンの法則 今でこそ当たり前の静電気や導体、絶縁体、電荷など
どういう経緯で発見し、クーロンの法則まで至ったのかの話です。
クーロン力、電場、近接作用 4つの力のうち、クーロン力の位置づけ
電荷が作り出す作用の電場。近接作用の話です。
微分、全微分、方向微分 簡単な微分、全微分、方向微分の話です。
ここをしっかり押さえないと、電磁気の数式の意味が
わからなくなります。
ベクトル解析 電磁気に必要なベクトル解析の話です。
勾配(grad)、2次元のグリーン定理
ストークスの定理の話です。
電位ポテンシャル 電位ポテンシャルです。勾配と電場の関係を使って説明しています。
電気双極子 電気双極子の話です。
物質中で起こる分極を理解するのに必要です。
ガウスの法則 ガウスの法則の積分形、微分形の話です。
ポアソンの方程式、ラプラス方程式 ポアソンの方程式、ラプラス方程式の話です。
単に電荷分布から電位を求めるだけの話にとどまらない
奥が深い分野です。ポテンシャル論、デルタ関数
グリーン関数、固有値問題について触れています。
静電場と渦なしの法則 静電場で、電荷を1周させた時の仕事はゼロ
微分形と微分形の渦なしの法則の話です。
ビオサバールの法則 電気と磁場の関係の発見の話から
ビオ・サバールの法則が導かれるまでの話です。
磁気双極子 磁気双極子の話で、回転電流になります。
物質中の磁場の話にも関連します。
アンペールの法則 アンペールの法則の話です。
積分形・微分形だけでなく、閉回路に流れる電流が作る
磁気双極子の話なども書いています。
ローレンツ力 磁場中を移動する電荷にかかる力(ローレンツ力)の話です。
ローレンツ力は相対性理論が絡んでいる事も紹介しています。
ファラデーの誘導起電力の法則 ファラデーの誘導起電力の話です。
うず電流を使った簡単な物理実験 電力計に使われるアラゴの円盤。
そしてIH調理器で熱するために発生させる、うず電流は
レンツの法則から電流が発生する原理を応用した物だ。

アラゴの円盤の実験と、IH調理器を使った実験です。
気分転換で読んでください。
ベクトルポテンシャル わかりにくいベクトルポテンシャルの話です。
電位は電荷が作る電気のポテンシャルだが
ベクトルポテンシャルは電流が作る磁場のポテンシャルの話です。
オームの法則の微分形 微小領域でのオームの法則の話です。
マックスウェルの方程式 4つのマックスウェルの方程式を書いています。
電場と磁場の変化を図にする事で
rotの回転の意味も理解できます。
ゲージ変換 ゲージ(gauge)は物差しの意味です。
マックスウェルの方程式をE（電場）とB(磁場)の関係式から
φ(電位ポテンシャル)とA(ベクトルポテンシャル)の関係式に
書き換える際、ゲージ変換が使われます。
ゲージ変換の役目を書きました。
電磁波 マックスウェルの方程式から電波が伝わる様子を
視覚的に見てみる話です。
回転のrotはベクトルの微分 ベクトル解析や渦なしの法則で出てくるrotは
ベクトルの微分という話です。
電磁気学の単位系 電磁気学の単位系の話です。
物理量の単位系の指数を見る次元解析
電磁気学の歴史と単位系の変遷について触れました。
電気泥棒:電気と法律の話 電気は物体なのか、無形物なのか。
明治時代に、電気を無断で使った場合、物か、そうでないかで
窃盗罪になるかどうかが裁判で問われました。
ちょっとした科学と法律の話です。気分転換で読んでください。
数ベクトルと基底ベクトル ベクトルの話です。
矢印だけがベクトルでない事。
数ベクトルと基底ベクトルの違いの話です。
多様体、反変・共変ベクトルを理解するのに必要です
多様体 空間を一般化した話です。
▽(ナブラ)の正体に迫まります
外積代数 外積、テンソルについて書いています。
極性ベクトル、軸性ベクトル
外積は行列で、ベクトルは見せかけの姿だった話です。
ベクトルの双対関係 反変ベクトル、共変ベクトル、双対関係
ベクトル解析、外積代数の話
外積、テンソルについて書いています。
ローレンツ力と相対性理論 磁場は電場の相対論的効果だった話です。
ローレンツ力を使って、導線が作る磁場を使って説明です。
微分形式 多様体の話の続きです。
座標に依存しない形での関数やベクトルの微分の話です。
ガウスの法則、アンペールの法則、マックスウェルの方程式が
鮮やかな形で表現できます。
∇(ナブラ)の正体もわかります。
物理と対称性 マックスウェルの方程式をよく見ると対称性があります。
物理の方程式と対称性を数学的な観点でみると
意外なつながりがあるという話です。
マックスウェルの応力 電気力線を弾性体(ゴム)とみなして、力の伝わり方などを
説明した考え方です。
電場エネルギー 電場が持つエネルギーの式を導いた話です。
磁場エネルギー 磁場が持つエネルギーの式です。
手抜きの説明と、直流RL回路を使った説明を書きました。
ポインティングベクトル 電磁エネルギーの流れ「ポインティングベクトル」の話です。
電磁波でもエネルギー保存則が成り立つ話から
ポインティングベクトルを導いています。
電気エネルギーは導線の外を伝わる 導線の外を電気エネルギーが流れる話です。
私が誤解した事、その誤解を解いていく過程を紹介しながら
「目からウロコ」にたどり着いた話です。
物質中の電場 物質中の電場の話です。
分極の話をしながら、物質中の電場の話をします
物質中の磁場 磁性の話をしながら、物質中の磁場の話をします
物質中のマックスウェルの方程式 物質中でもマックスウェルの方程式が成り立つ話です。
導体に侵入する電磁波 導体に侵入する電磁波が減衰していく話です。
表皮効果と同じ「表皮の厚さ」が出てきます
表皮効果 目的の表皮効果の話です。

マックスウェルの方程式を解きながら
交流電流の周波数を上げると、表面にしか電流が流れなくなる話です。
電磁気学の目次:「電磁気学入門」に戻る

前章:「無線LANの基礎 無線LAN入門と導入事例」を読む
システム奮闘記の目次:システム奮闘記に戻る
トップ:オープンソース(OSS)で中小企業のIT化に戻る
v
v