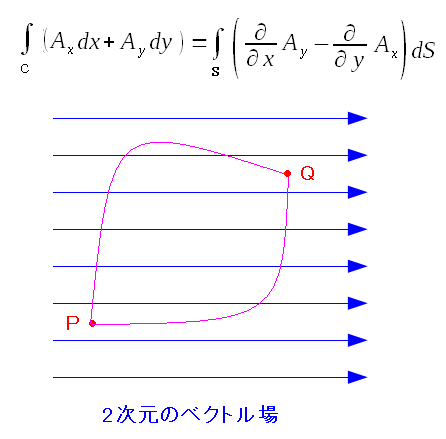
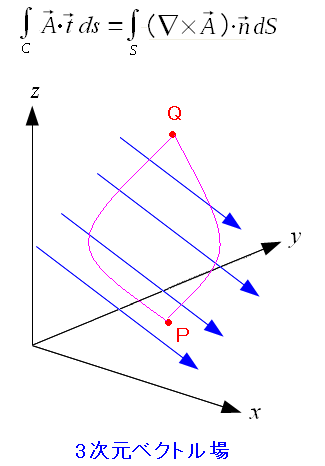
ベクトル場において、P→Qへ線積分した際(左辺)
経路に関係なく同じ値になるための条件が
右辺になるというのだ。
システム奮闘記:その105
(2016年5月22日に掲載)
ベクトル解析
電磁気学で重要になるのは勾配のgrad。 そしてグリーンの定理とストークスの定理。 グリーンの定理、gradの勾配、ストークスの定理の順番に説明していく。 ベクトル解析の本だと、数式ばかりでわかりにくい上 電位を使った説明だと、目に見えないだけに、わかりにくい。 そこで全微分の時に温度を使った話で説明する。
2次元のグリーンの定理
2次元のグリーンの定理なのだが、なぜ「2次元」という枕詞をつけるのか。 なぜなら・・・ 他にもグリーンの定理があるのらー!!
| 2次元のグリーンの定理について |
|---|
|
別名「平面のグリーンの定理」とも呼ばれる ベクトル解析などの数学書には出てくる定理なのだが 電磁気の本では、軽く触れる程度だったり 名前が出てこない場合もある。 今から説明する「2次元のグリーンの定理」は 数学で言うグリーンの定理になるのだ。 |
というわけで混乱を避けるため、ここでは「2次元」という枕詞をつけて 話を進めていく事にする。
| 2次元のグリーンの定理の式 |
|---|
 |
|
一般的なベクトル解析の本だと、上図のように ベクトル場において、P→Qへ線積分した際(左辺) 経路に関係なく同じ値になるための条件が 右辺になるというのだ。 |
だが、数学書だと・・・ 抽象的でわからへん! なのだ。 誤解のないように書くが、抽象的な内容を書いている 著者を批判する意図はないし、数学科の先生を批判する気はない。 要するに・・・ 私の頭だと抽象的な説明が理解できへんのだ!! そこで具体的な例として、微分、全微分、方向微分の話で出てきた熱分布を用いて説明する事にした。
| 火を使って平面(板)を熱した時の平面(板)の温度分布 |
|---|
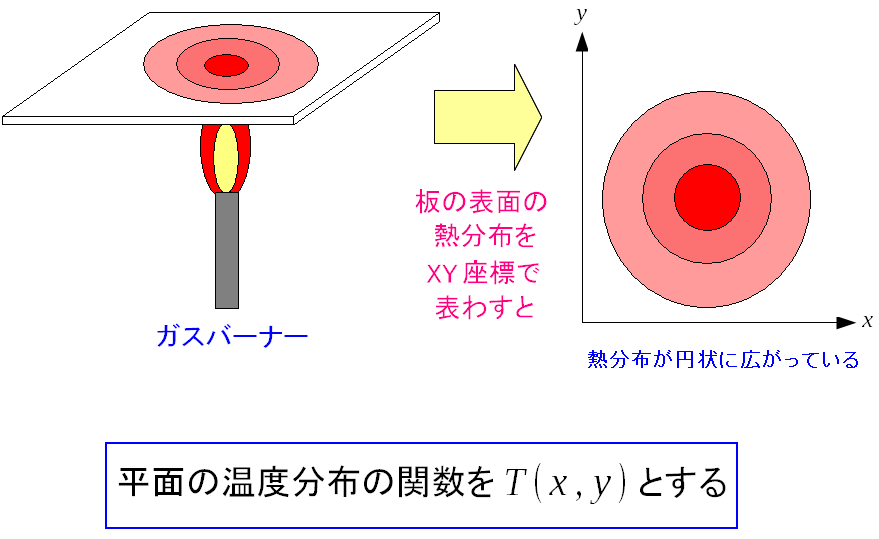 |
| 2変数(XY平面)の例として、これが一番かなぁと思ったりする。 |
さて、板を熱した際、同心円状に温度分布ができる 微小領域を選んで、経路による温度上昇度を見てみる。
| 経路に関係なく温度上昇は同じ |
|---|
 |
|
P→Qへ移動する際、2つの経路がある。 どっちの経路を使っても、温度上昇は同じなのだ。 そのためP→A→Q→B→Qと一周すると、温度上昇はゼロになる。 ただし経路は反時計回りになるようにする。 |
ところで・・・
なんで反時計回りやねん!!
なのだ。
どっち回りでもゼロになれば問題ないはず。
なぜ反時計回りにこだわるのか。
| 反時計回りについて |
|---|
|
当初、反時計回りになる事すら疑問に思わなかった。 だが、この資料を作成していると、本に書いている式と 私が計算した物では符号が反対になっているのに気づき 反時計回りの経路になっている事がわかった。 あとに書いている外積代数の所で取り上げているが 直交座標系には右手系と左手系がある。 ここで出ている右手系の座標系の場合 反時計回りが正の方向の回転で、時計回りが負の方向のようだ。 |
ところで微小領域を2つ重ねるとどうなるのか?
| 微小領域を2つ重ねる |
|---|
 |
|
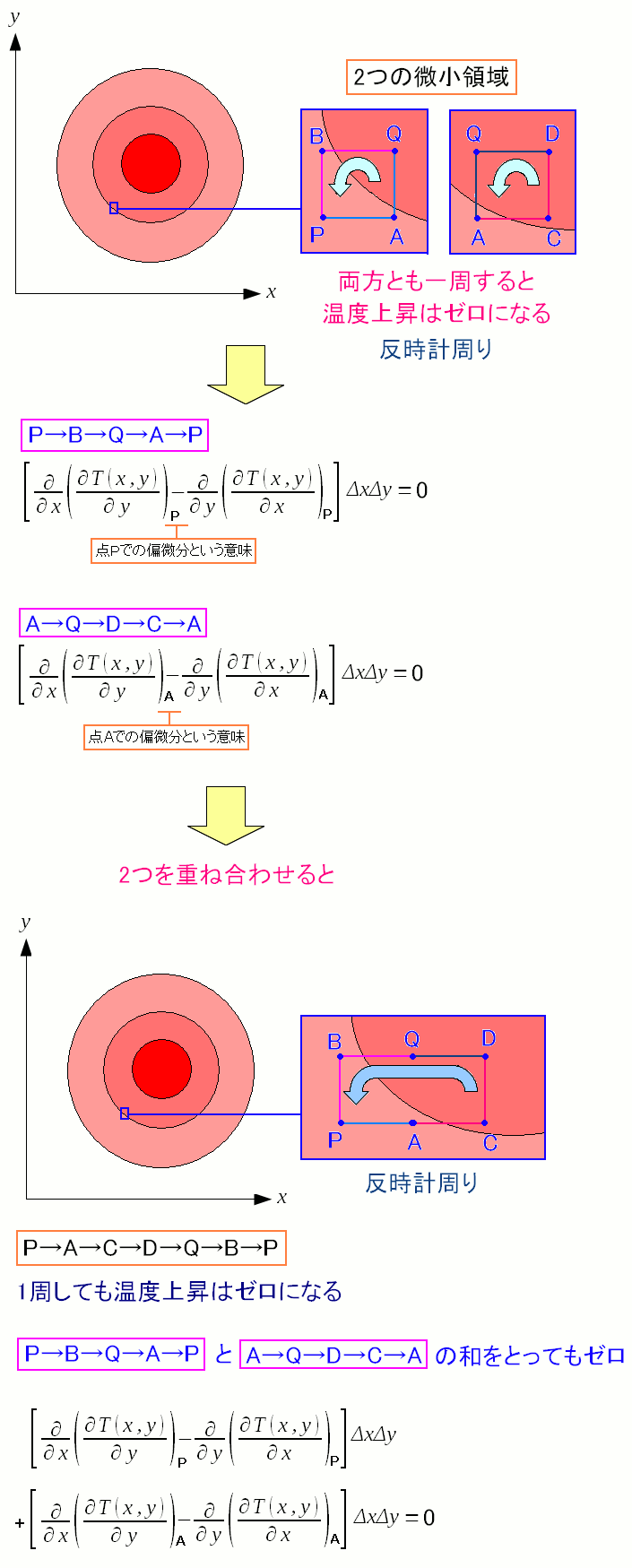
2つの微小領域の1周分した時の温度上昇の和はゼロ。 微小領域を2つ重ねて、外周を1周した場合の温度上昇はゼロになる。 |
微小領域を大量に重ねた場合を見てみる。
| 微小領域を大量に重ねた場合 |
|---|
 |
|
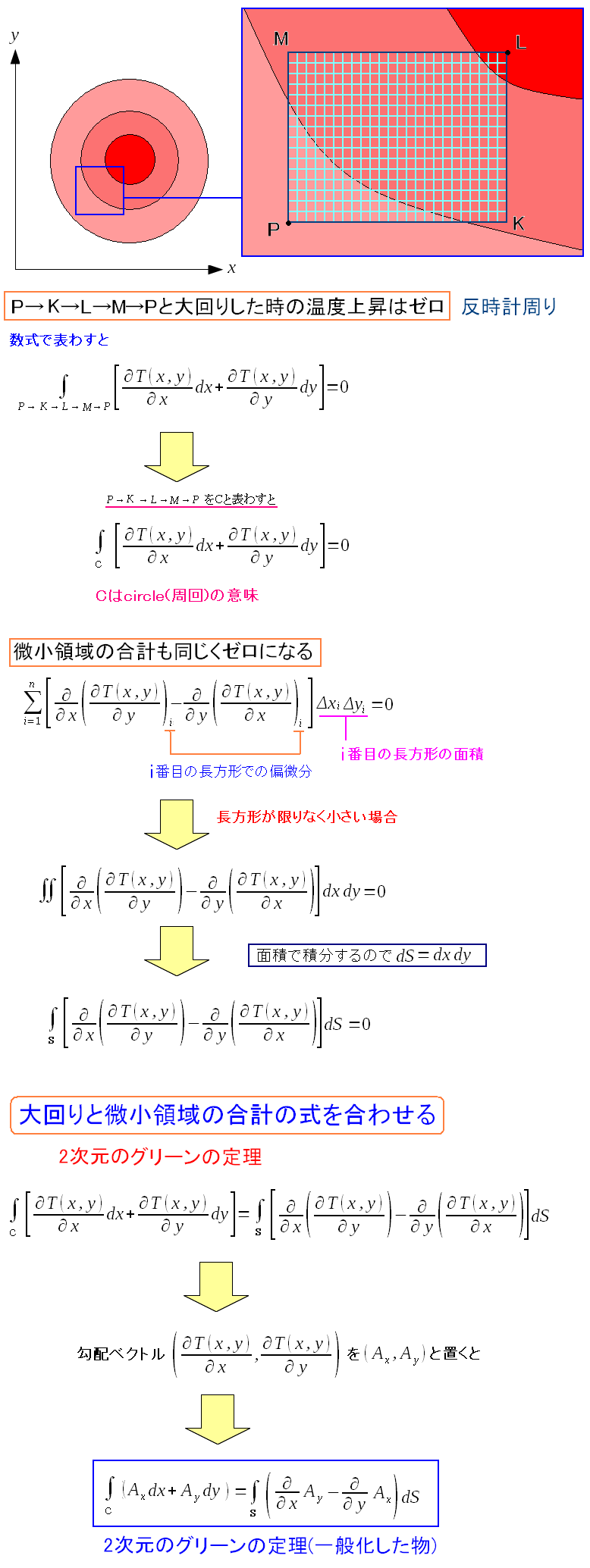
大回りしても温度上昇はゼロ。 個々の微小領域を一周した時の温度上昇の和を、合計したのもゼロ。 大回りした経路と、個々の微小領域を1周した物の合計が同じになる式が 2次元のグリーンの定理になる。 2次元のグリーンの定理は、ベクトル場で適用できる式だ。 |
この式を見た時は、何も思わなかった。 だが、ある資料に、次のような事が書いていた。 グリーンの定理、次に出てくるストークスの定理は・・・ 周辺の状態から、内部の状態を見る式 というのだ。 確かにある領域を大回りして変化がゼロの場合、内部の微小領域でも 同じ事が起こっている。 詳しい事は後述しています。
勾配の grad
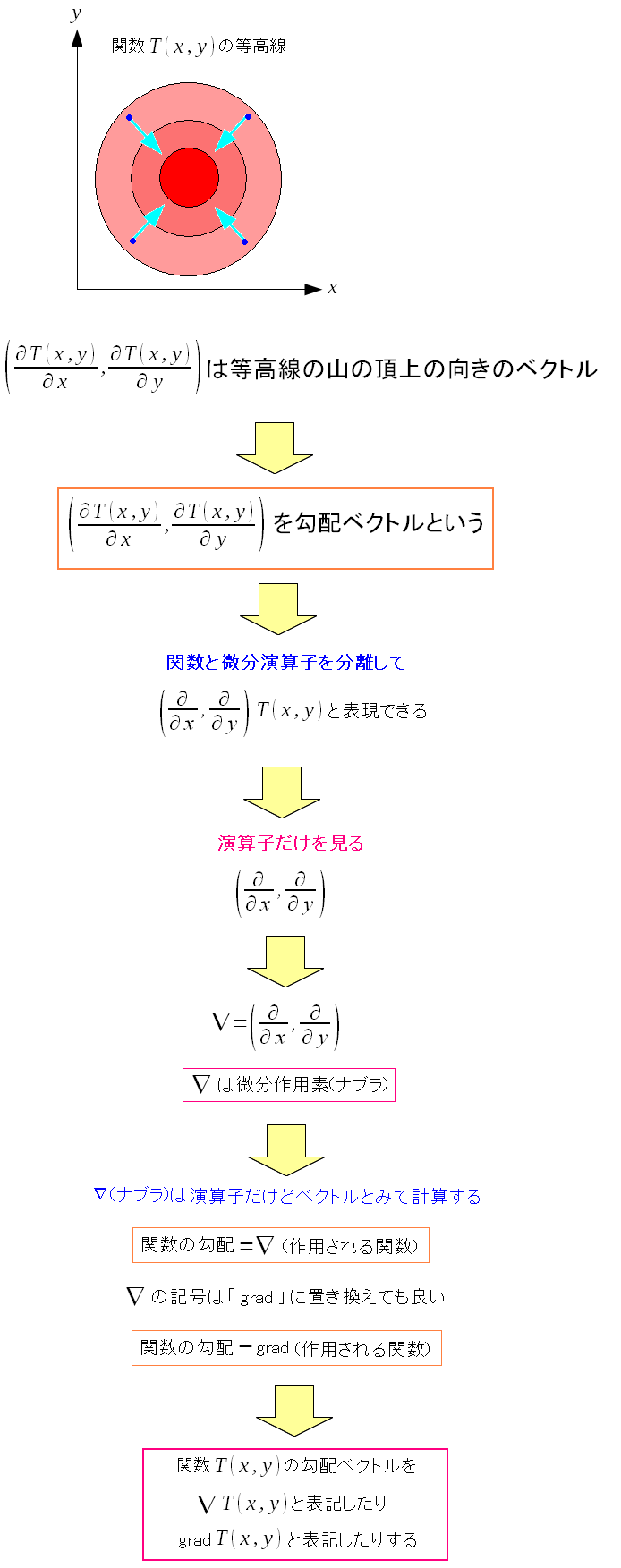
実は勾配の話は全微分の所で出てきたのだ。 勾配ベクトル なのだ。 ただ、ここで大事なのは勾配ベクトルではなく 関数の勾配を求める際の表記法なのだ。 まずは2次元の場合を考える。
| 勾配(grad)とは |
|---|
 |
|
grad そのものは、勾配ベクトルを表わすための表記法にすぎない。 勾配ベクトルを求める際、微分作用素を∇(ナブラ)を使って表現できる。 この先、どんどん∇が出てくるのだ。 |
ところで、多変数関数を全微分する事によって勾配ベクトルが求められる。
そして関数の値はスカラーなのだが、微分作用素を使う事で
スカラー関数をベクトルに変換
しているのだ。
学生時代、そんなことには気づかなかった。
いかに数学を勉強していなかった事がバレバレなのだ。
次に3次元の場合の関数の勾配を求める。
ここでも電荷の話に入らず熱を使った説明を行なう。
| 3次元の熱分布を考える |
|---|
 |
|
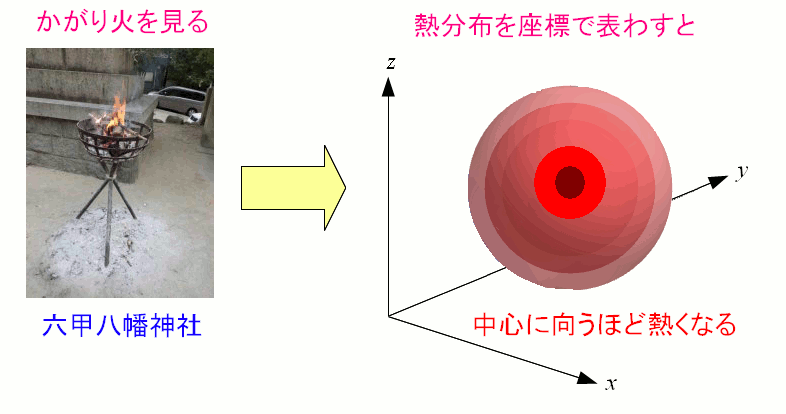
かがり火があると、その周囲は球状に熱の等高線ができる。 例に使うのに最適なのだ。 (余談) 六甲八幡神社の、かがり火だ。 神戸に住んでいた時の、近所の神社だ。 阪急六甲駅を拡張した時、八幡さんのご神木を切る事になったため それ以来、阪急電鉄とは険悪の関係という話があるようだが 真偽は定かではない。 |
かがり火の付近の領域で、2点間の温度差を求めてみる。
| かがり火の付近の領域で、2点間の温度差を求めてみる |
|---|
 |
|
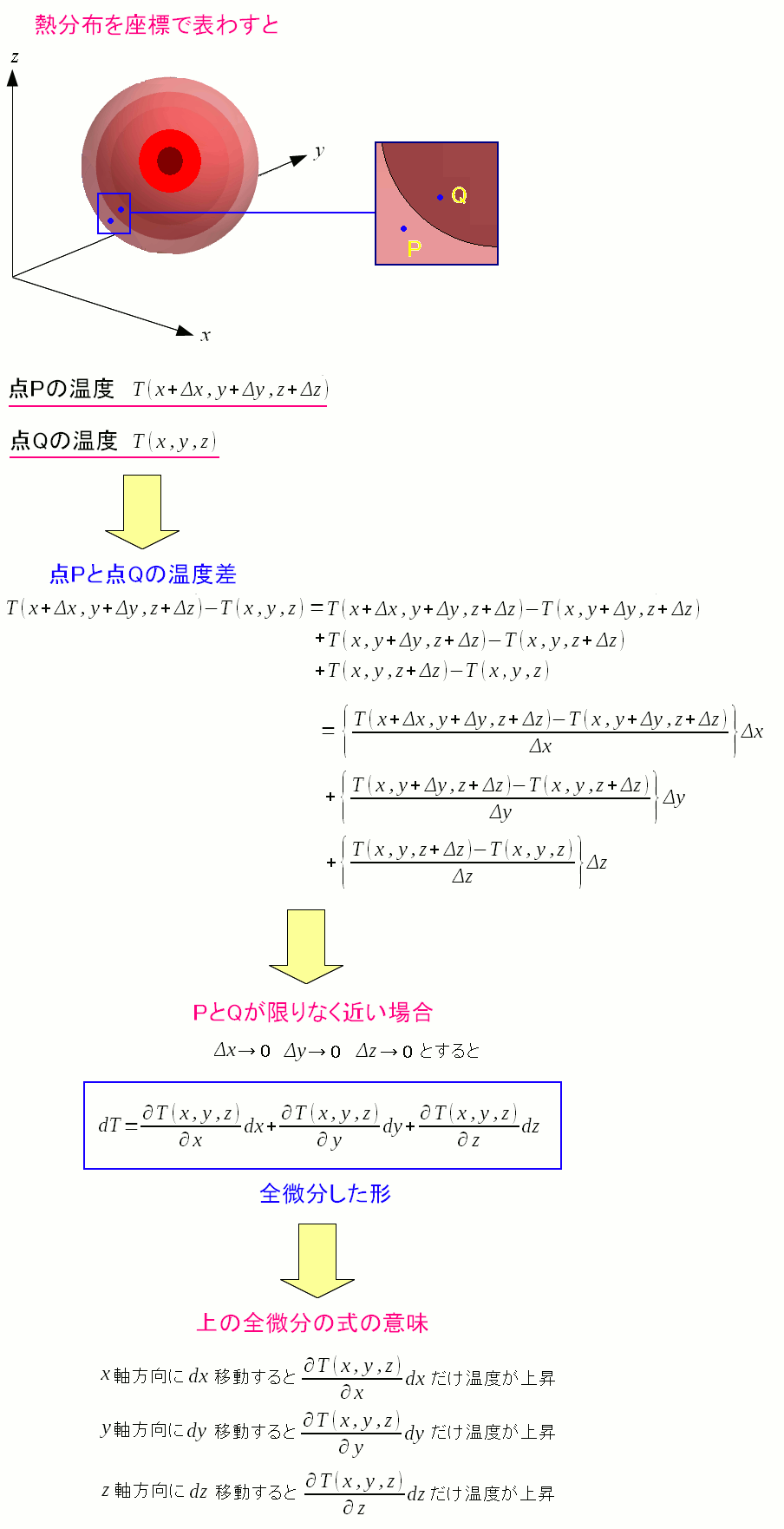
点Pと点Qの温度差を求めてみる。 全微分の式が求まる。 |
もし、2点間の温度差がゼロの場合を考える
| 2点間の温度差がゼロの場合を考える |
|---|
 |
|
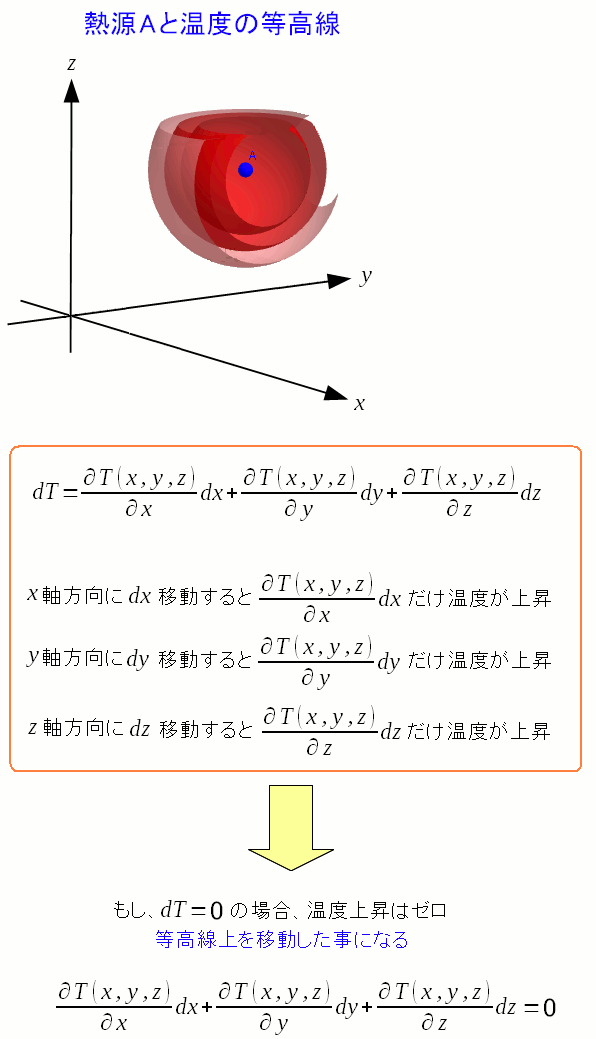
温度上昇がゼロの場合、動いていないか もしくは等高線上を移動している事になる、 |
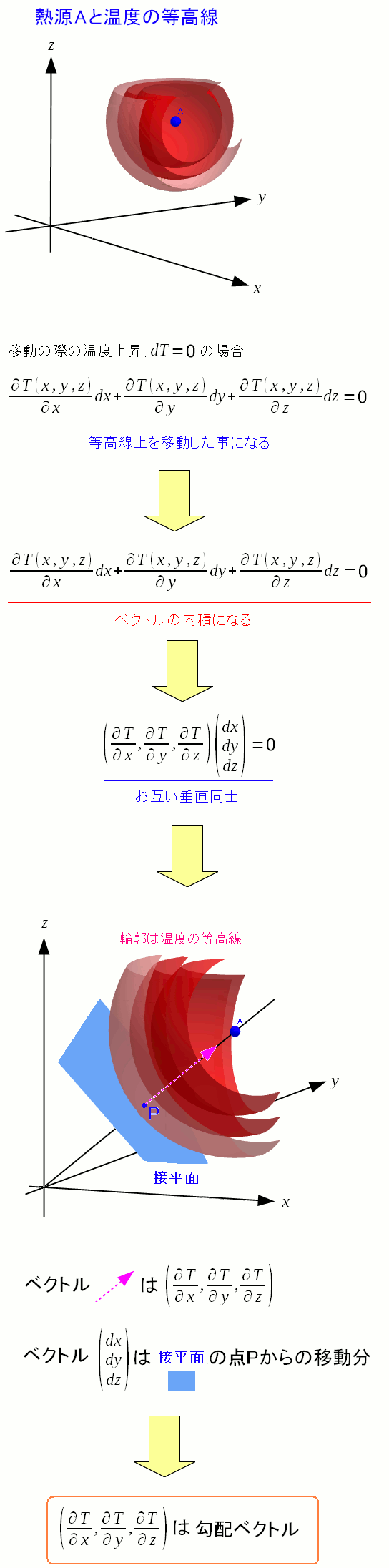
温度上昇がゼロの場合、移動方向と勾配ベクトルの関係を見てみる。
| 温度上昇がゼロの場合、移動方向と勾配ベクトルの関係 |
|---|
 |
|
温度等高線は球状になっている。 球の上を移動した場合、温度上昇がゼロになる。 勾配ベクトルは、球の表面に垂直方向(熱源の方)を向いている。 |
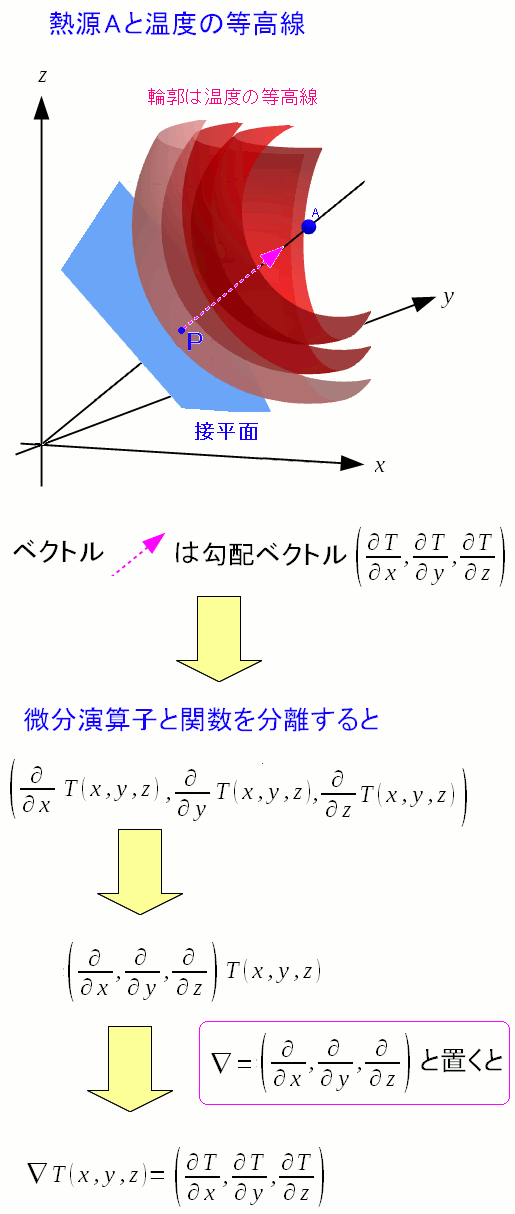
ところで、電磁気学では微分演算子の▽(ナブラ)を見る。 勾配の場合、▽(ナブラ)を使った以下の表現を行なう。
| ▽(ナブラ)を使って勾配を表現 |
|---|
 |
|
「▽T(x,y,z)」という表現で、関数T(x,y,z)に作用している形で 表現しているのだ。 |
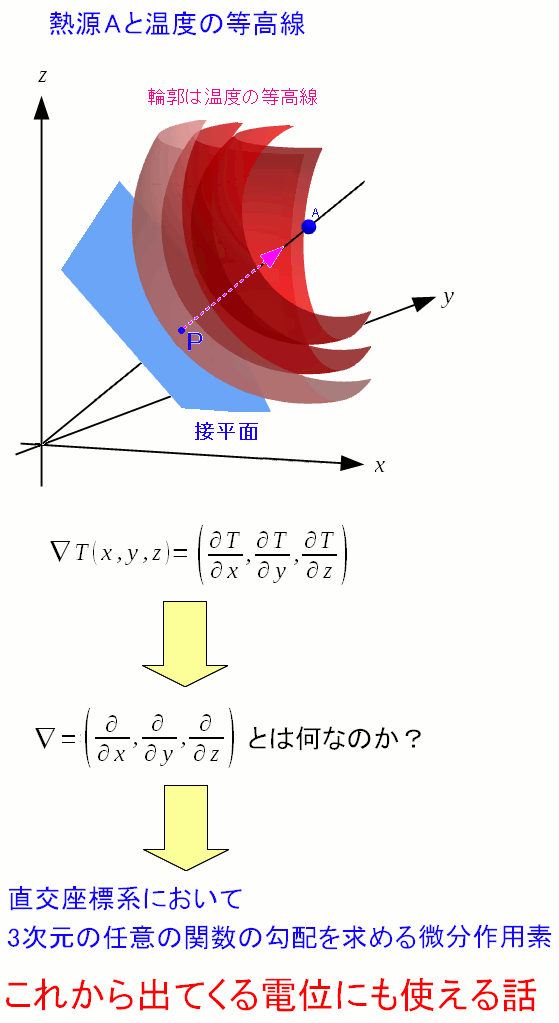
ところで、▽(ナブラ)とは、一体、何だろうと思いたくなる。
| ▽(ナブラ)とは、一体、何だろう |
|---|
 |
|
学生時代、電磁気学を習った時、▽(ナブラ)が出てきた。 その時は、単に計算上出てくる記号だと思っていた。 任意の3次元のスカラー関数から、勾配を求めるための 微分作用素だというのが、ここでわかった。 だが、これだけでは終わらない。 それについては後述していますので、お楽しみに!! |
ストークスの定理
2次元のグリーンの定理を3次元に拡張したのが ストークスの定理になる。
| ストークスの定理の式 |
|---|
 |
|
一般的なベクトル解析の本だと、上図のように ベクトル場において、P→Qへ線積分した際(左辺) 経路に関係なく、同じ値になるための条件が 右辺になるというのだ。 |
だが、抽象的な内容だと理解できないので、 ここでも、熱分布を例にして考えるのだ。 まずは3次元の場合の微小領域で見てみる。 長方形の端から端までの経路の温度上昇を求めてみるのだ。
| 3次元の場合の微小領域での温度上昇 |
|---|
 |
|
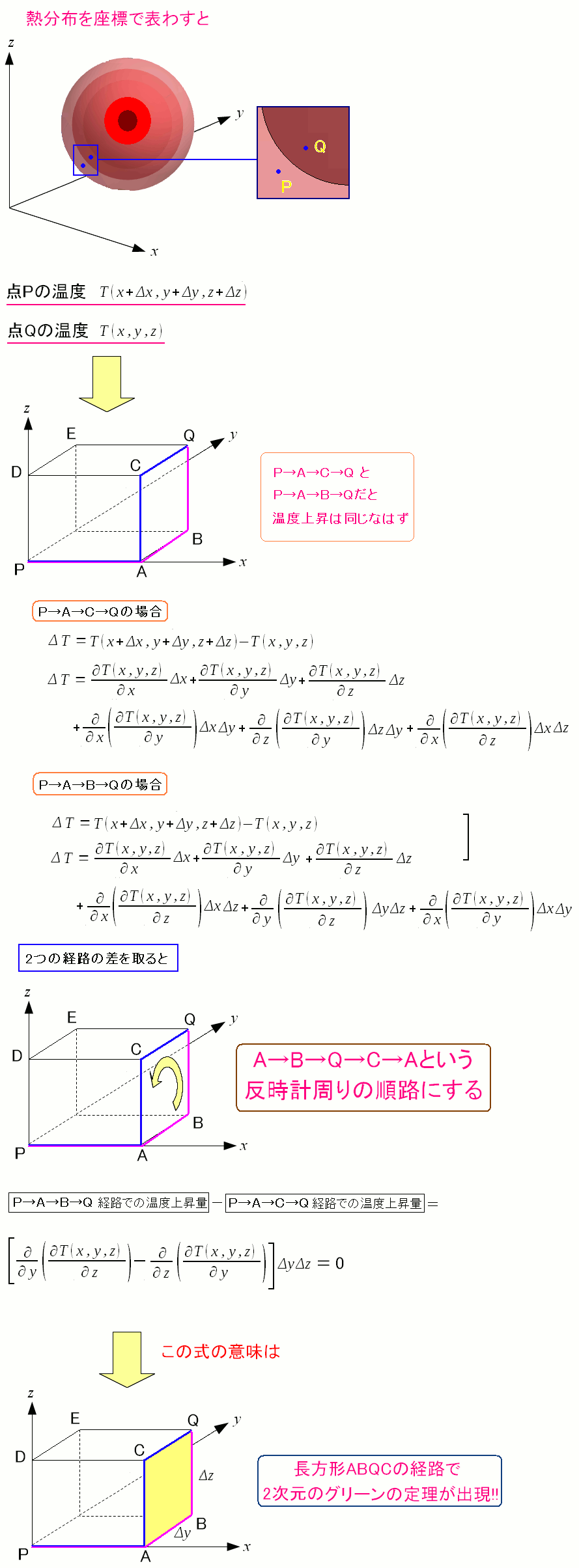
P→A→B→Qの経路での温度上昇を求めてみる。 なぜ、yz平面(長方形ABQC)を1周する形にしたのかは、すぐ後でわかります。 |
そして次に、もう1つの経路を求めてみる
| もう1つの経路での温度上昇 |
|---|
 |
| P→A→C→Qの経路での温度上昇を求めてみる。 |
そして求まった2つの経路での温度上昇の差から ぐるっと1周した時の温度上昇を求めてみる。
| 1周した時の温度上昇について |
|---|
 |
|
ぐるっと1周して元に戻るため、温度上昇はゼロになる。 ただし、2つの式は異なるため、式の差が出てくる。 この時の式の差は、長方形ABQCの経路を1周した時の 2次元のグリーンの定理の形になっている。 |
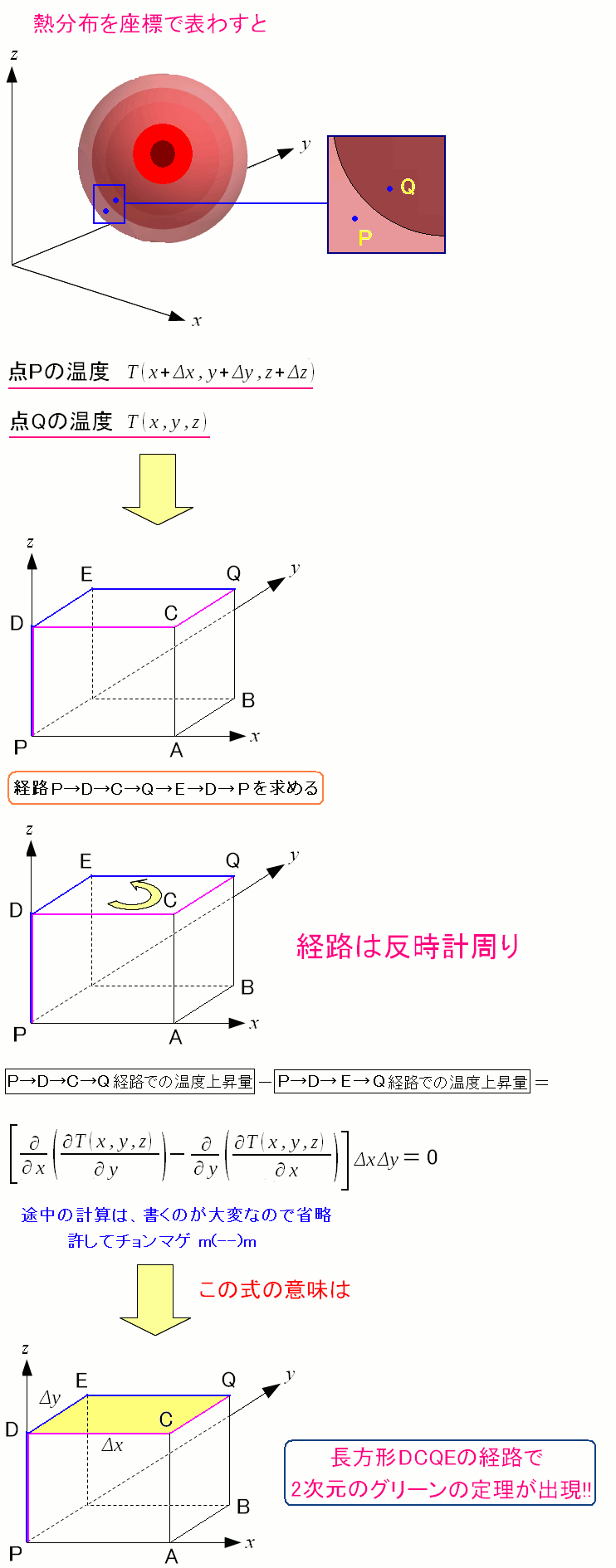
点Pと点Qまでの経路は、何通りもある。 そこで別の経路の差で考えてみる。
| DCQEを1周する経路で考えてみる |
|---|
 |
|
この場合、長方形DCQEの経路を1周した時の 2次元のグリーンの定理の形になっている。 |
今度は、長方形PACDを1周した形で考えてみる。
| 長方形PACDを1周した形で考えてみる |
|---|
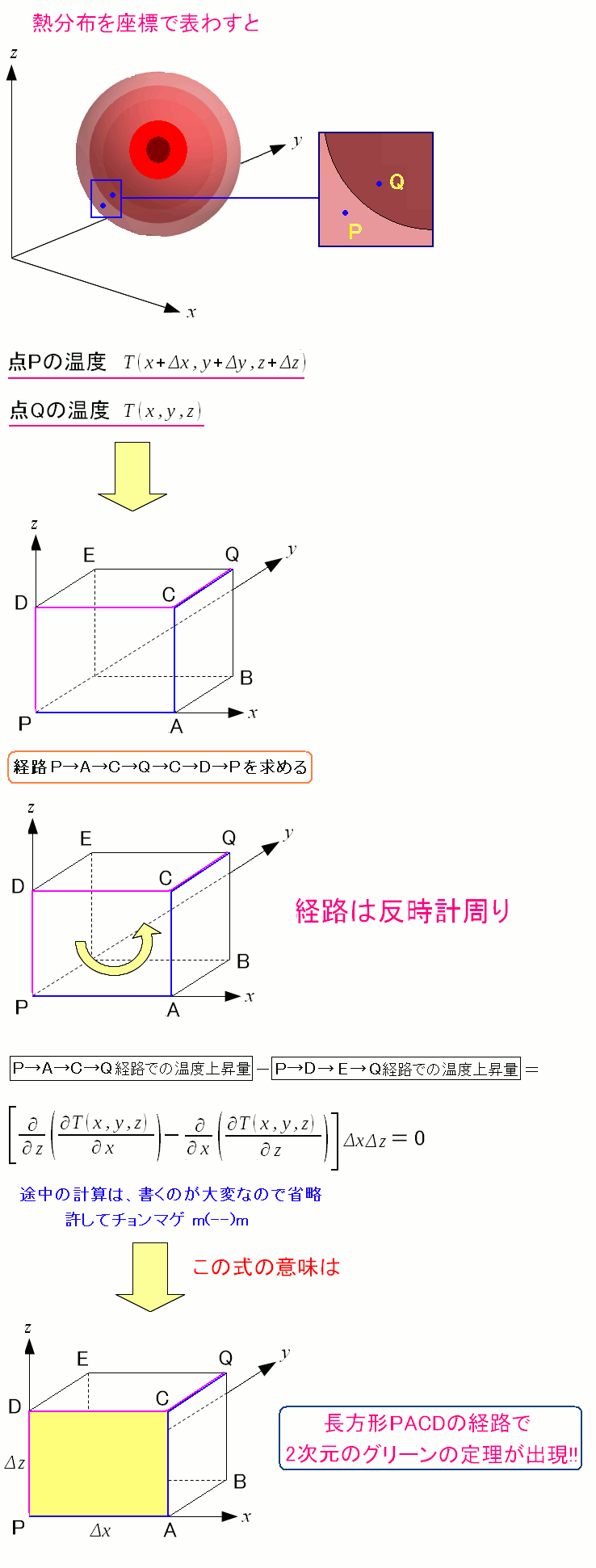 |
| 長方形PACDを1周した時の2次元のグリーンの定理の形になっている。 |
ここで、以下の事に気づく人は多いと思う。
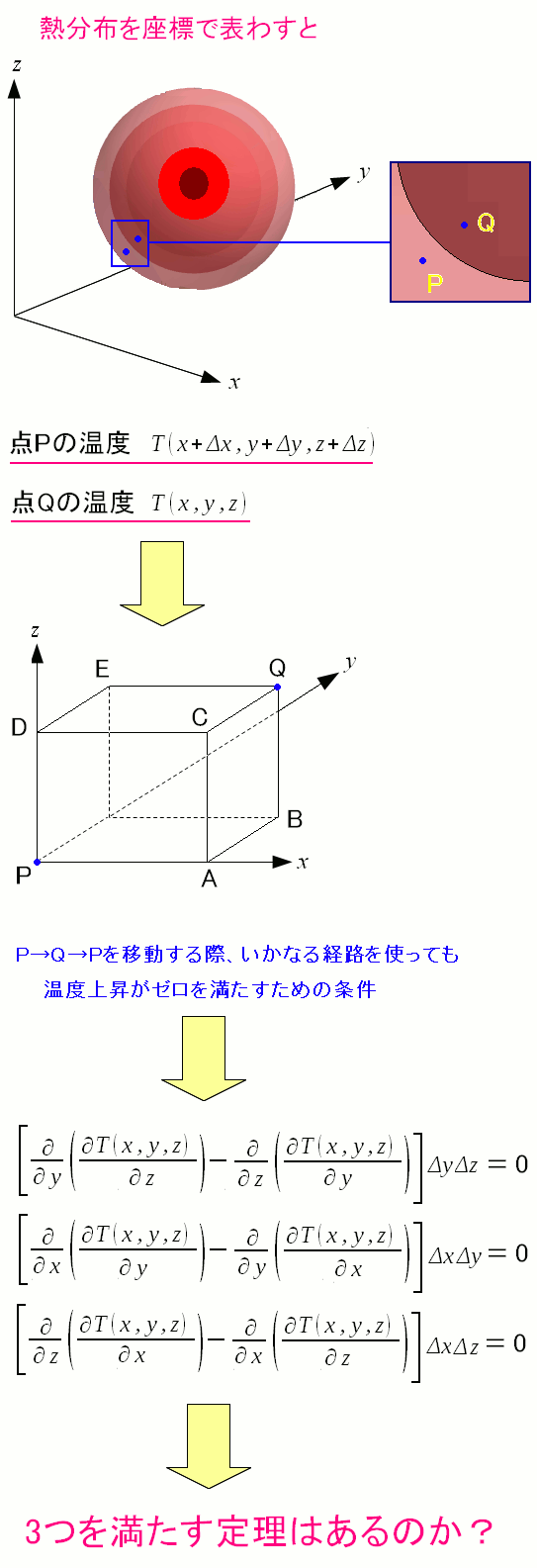
3次元の経路を考える場合、いかなる経路を通っても同じという事を言うには
3つの2次元のグリーンの定理を満たす必要があるのでは?
| 3つの2次元のグリーンの定理を満たす必要があるのでは? |
|---|
 |
|
3つの2次元のグリーンの定理を同時に満たしてこそ いかなる経路を通っても、温度上昇の変化は同じと言えるのではないか。 だが、ここまでの話では、同時に満たす式を導いていない。 |
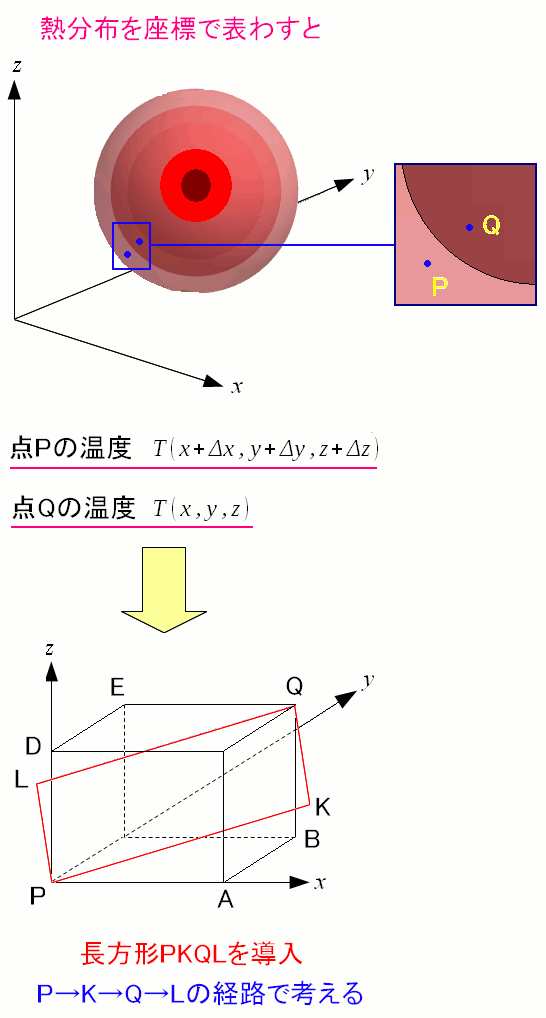
そこで経路にあたる長方形が、任意の方向を向いている場合を考えてみる。 そこで以下の場合を考えてみた。
| 経路にあたる長方形が任意の方向を向いている場合 |
|---|
 |
|
経路に当たる長方形が斜め向いている。 長方形の辺が、どの軸にも並行にならないようにすれば 経路による温度差の式が、任意の場合に成り立つ式になると考える。 |
計算してみる。
| 長方形PKQLの1周した時の温度上昇の計算・第1段階 |
|---|
 |
|
ここではP→KとQ→Lの場合の温度上昇の和を求めてみた。 並行する辺同士の温度上昇の和を計算するのは 計算を楽にするためなのだ。 |
残り2辺の計算を行なう。
| 長方形PKQLの1周した時の温度上昇の計算・第2段階 |
|---|
 |
| K→QとL→Pの温度上昇の和を求めてみた。 |
2つの「2つの辺での温度上昇」が出てきたので、それの和を求める。 すると3つの「2次元のグリーンの定理」を含んだ式が求まる。 その前に、ストークスの定理には外積(クロス積)が出てくるので 外積を軽く説明する。
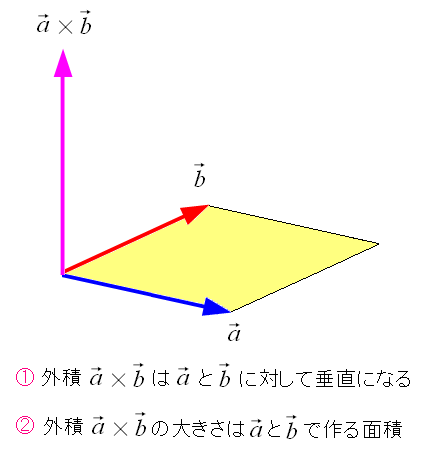
| 外積(クロス積)の定義 |
|---|
 |
|
大学の理工系なら線形代数で習う外積(クロス積)。 2つのベクトルの積が、2つのベクトルに垂直方向で しかも2つのベクトルが作る平行四辺形の面積になる物だ。 「なぜそうなるのか」の質問はしてはいけない。 外積(クロス積)の計算規則なので、決まりとして受け入れるのだ。 (注意) 線形代数では外積といえば上に書いているクロス積の事を指す。 だが外積には、もう1つ、ウェッジ積というのがある。 それについては外積代数の所で書いています。 |
外積の定義をしたので、ストークスの式を見てみる。
| 経路PKQLでの温度上昇 |
|---|
 |
| 3つの「2次元のグリーンの定理」を含んだ式が求まる。 |
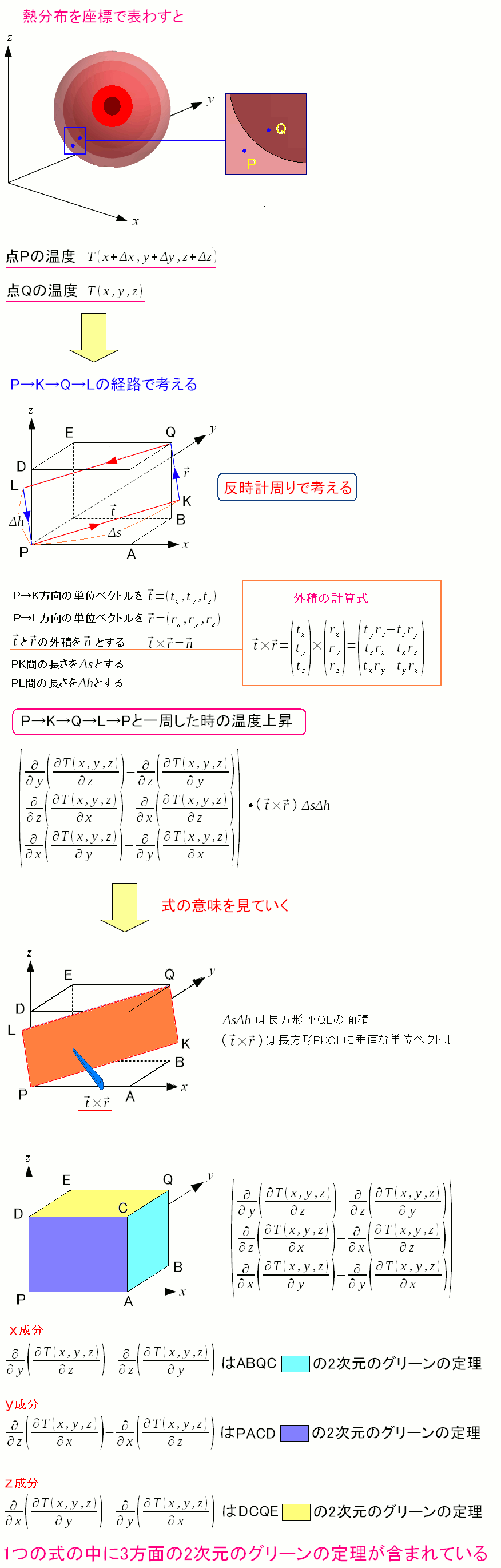
この式の意味を考える。
| 求まった式の意味を考える |
|---|
 |
|
求まった面積は長方形の面積だ。 ベクトルは長方形の平面に垂直方向のベクトルになる。 |
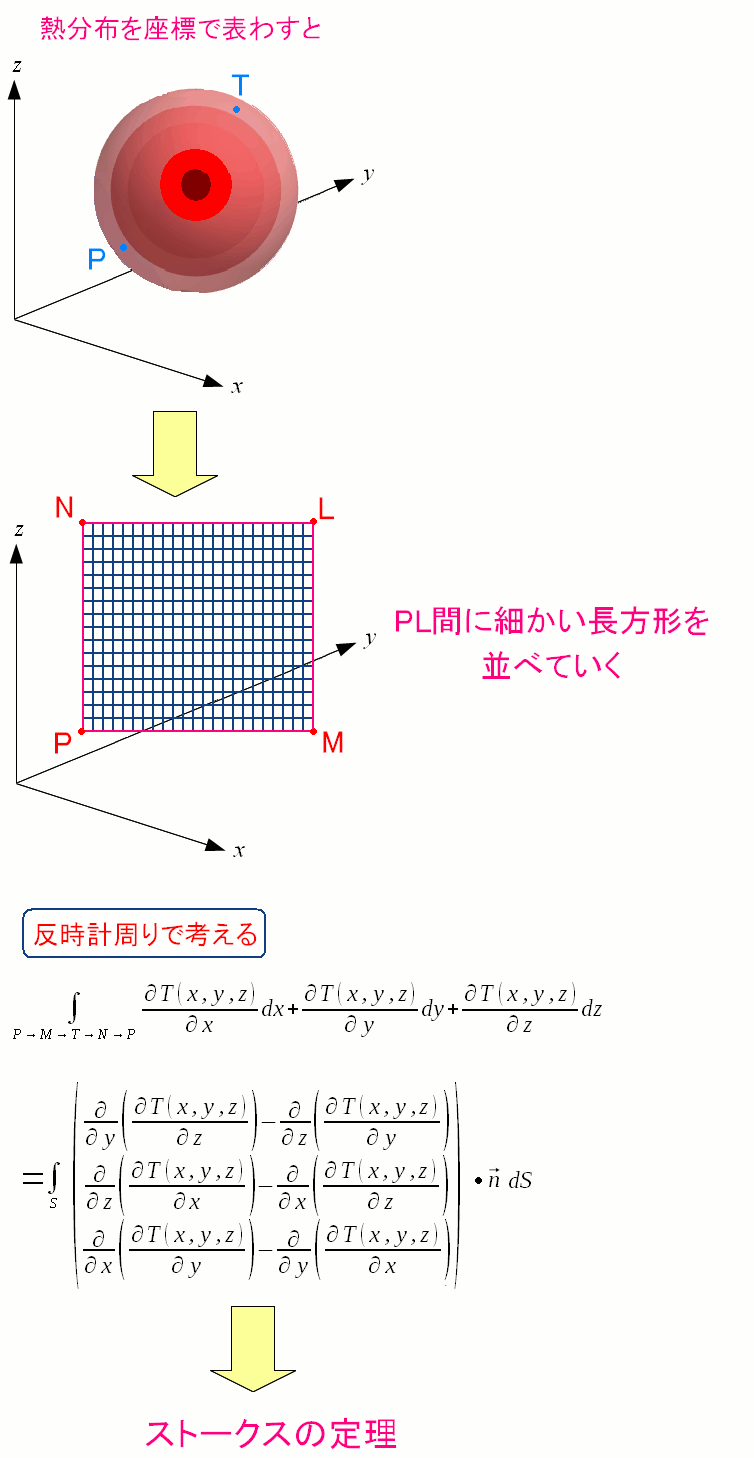
微小な長方形を寄せ集めた場合を考える。
| 微小な長方形を寄せ集めた場合を考える |
|---|
 |
|
大回りした場合の温度上昇はゼロ。 微小な長方形を1周した時も温度上昇はゼロ。 微小な長方形の温度上昇の和もゼロ。 3次元版の「2次元のグリーンの定理」が求まる。 この式がストークスの定理になるのだ。 |
3つの「2次元のグリーンの定理」を含んだ式が
ストークスの定理
なのだ。
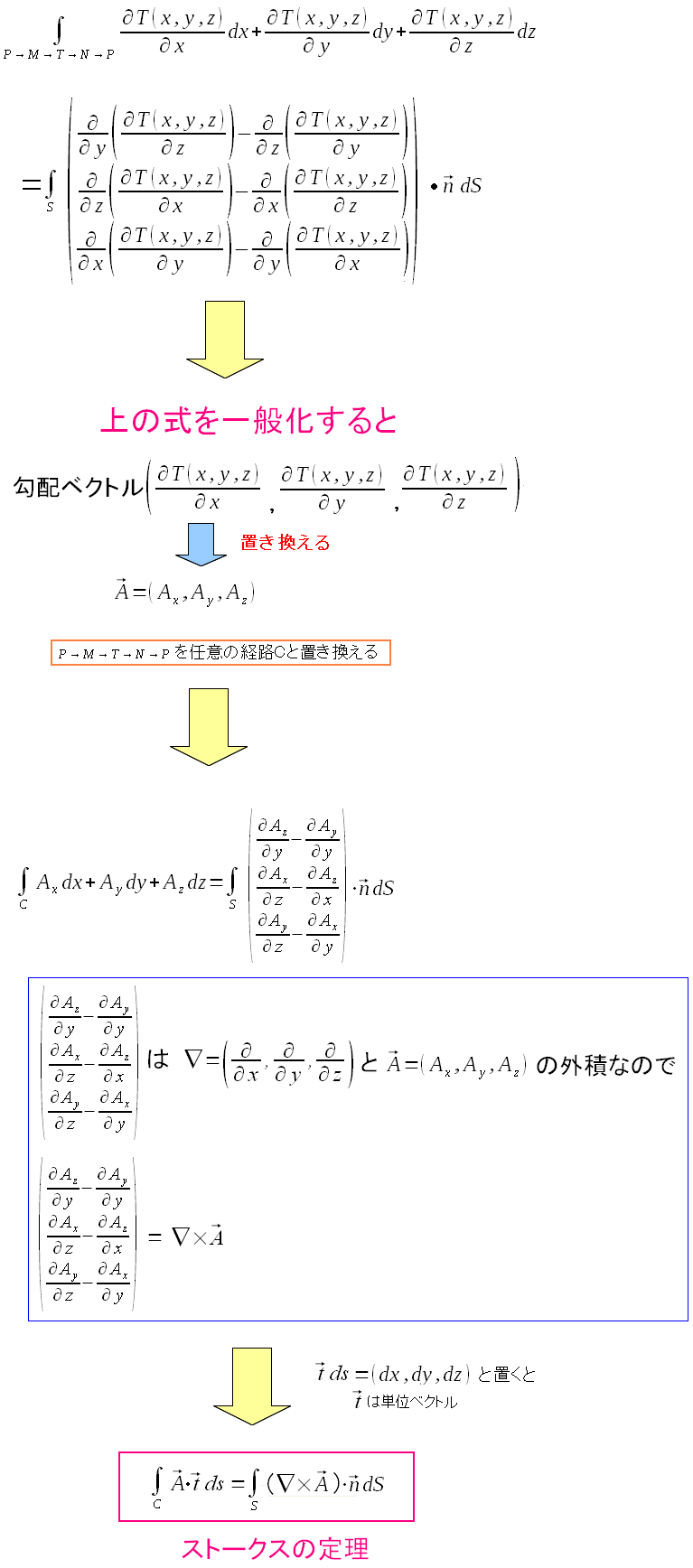
| 求まったストークスの定理を一般化すると |
|---|
 |
|
ベクトル場において、閉曲面の外周を1周する際に足し合わせたベクトルと、 閉曲面内で細切れにした微小な領域(面積)と、その面と垂直方向のベクトルの積を 合計した物が同じという意味だ。 ところで微分作用素で、スカラー関数の勾配を求める∇(ナブラ)が出てきた。 でも、ここでは、微分作用素がベクトルの形になっていて ベクトルと同じ計算が成り立つという事だけに留めます。 ∇(ナブラ)については後述していますので、お楽しみにしてください。 |
ここで出でくる疑問。 ストークスの定理は何に使えるねん? 確かに、このままでは無味乾燥で、意味不明になってしまう。 だが、電場や磁場の状態を表現するのに適用すれば ストークスの定理が、具体的な意味を帯びた式になってくる。 その話は静電場と渦なしの法則で取り上げます。
電磁気学入門の目次
| 電磁気学入門:目次 | |
|---|---|
| スカラーとベクトル | 簡単なスカラーとベクトルの話です。 ベクトルは方向と大きさを持つ量。方向という量持っているだけに注意が必要です。 |
| 静電気の発見からクーロンの法則 | 今でこそ当たり前の静電気や導体、絶縁体、電荷など どういう経緯で発見し、クーロンの法則まで至ったのかの話です。 |
| クーロン力、電場、近接作用 | 4つの力のうち、クーロン力の位置づけ 電荷が作り出す作用の電場。近接作用の話です。 |
| 微分、全微分、方向微分 | 簡単な微分、全微分、方向微分の話です。 ここをしっかり押さえないと、電磁気の数式の意味が わからなくなります。 |
| ベクトル解析 |
電磁気に必要なベクトル解析の話です。 勾配(grad)、2次元のグリーン定理 ストークスの定理の話です。 |
| 電位ポテンシャル | 電位ポテンシャルです。勾配と電場の関係を使って説明しています。 |
| 電気双極子 |
電気双極子の話です。 物質中で起こる分極を理解するのに必要です。 |
| ガウスの法則 | ガウスの法則の積分形、微分形の話です。 |
| ポアソンの方程式、ラプラス方程式 |
ポアソンの方程式、ラプラス方程式の話です。 単に電荷分布から電位を求めるだけの話にとどまらない 奥が深い分野です。ポテンシャル論、デルタ関数 グリーン関数、固有値問題について触れています。 |
| 静電場と渦なしの法則 |
静電場で、電荷を1周させた時の仕事はゼロ 微分形と微分形の渦なしの法則の話です。 |
| ビオサバールの法則 |
電気と磁場の関係の発見の話から ビオ・サバールの法則が導かれるまでの話です。 |
| 磁気双極子 |
磁気双極子の話で、回転電流になります。 物質中の磁場の話にも関連します。 |
| アンペールの法則 |
アンペールの法則の話です。 積分形・微分形だけでなく、閉回路に流れる電流が作る 磁気双極子の話なども書いています。 |
| ローレンツ力 |
磁場中を移動する電荷にかかる力(ローレンツ力)の話です。 ローレンツ力は相対性理論が絡んでいる事も紹介しています。 |
| ファラデーの誘導起電力の法則 | ファラデーの誘導起電力の話です。 |
| うず電流を使った簡単な物理実験 | 電力計に使われるアラゴの円盤。 そしてIH調理器で熱するために発生させる、うず電流は レンツの法則から電流が発生する原理を応用した物だ。 アラゴの円盤の実験と、IH調理器を使った実験です。 気分転換で読んでください。 |
| ベクトルポテンシャル |
わかりにくいベクトルポテンシャルの話です。 電位は電荷が作る電気のポテンシャルだが ベクトルポテンシャルは電流が作る磁場のポテンシャルの話です。 |
| オームの法則の微分形 | 微小領域でのオームの法則の話です。 |
| マックスウェルの方程式 |
4つのマックスウェルの方程式を書いています。 電場と磁場の変化を図にする事で rotの回転の意味も理解できます。 |
| ゲージ変換 |
ゲージ(gauge)は物差しの意味です。 マックスウェルの方程式をE(電場)とB(磁場)の関係式から φ(電位ポテンシャル)とA(ベクトルポテンシャル)の関係式に 書き換える際、ゲージ変換が使われます。 ゲージ変換の役目を書きました。 |
| 電磁波 |
マックスウェルの方程式から電波が伝わる様子を 視覚的に見てみる話です。 |
| 回転のrotはベクトルの微分 |
ベクトル解析や渦なしの法則で出てくるrotは ベクトルの微分という話です。 |
| 電磁気学の単位系 | 電磁気学の単位系の話です。 物理量の単位系の指数を見る次元解析 電磁気学の歴史と単位系の変遷について触れました。 |
| 電気泥棒:電気と法律の話 |
電気は物体なのか、無形物なのか。 明治時代に、電気を無断で使った場合、物か、そうでないかで 窃盗罪になるかどうかが裁判で問われました。 ちょっとした科学と法律の話です。気分転換で読んでください。 |
| 数ベクトルと基底ベクトル | ベクトルの話です。 矢印だけがベクトルでない事。 数ベクトルと基底ベクトルの違いの話です。 多様体、反変・共変ベクトルを理解するのに必要です |
| 多様体 | 空間を一般化した話です。 ▽(ナブラ)の正体に迫まります |
| 外積代数 |
外積、テンソルについて書いています。 極性ベクトル、軸性ベクトル 外積は行列で、ベクトルは見せかけの姿だった話です。 |
| ベクトルの双対関係 |
反変ベクトル、共変ベクトル、双対関係 ベクトル解析、外積代数の話 外積、テンソルについて書いています。 |
| ローレンツ力と相対性理論 |
磁場は電場の相対論的効果だった話です。 ローレンツ力を使って、導線が作る磁場を使って説明です。 |
| 微分形式 |
多様体の話の続きです。 座標に依存しない形での関数やベクトルの微分の話です。 ガウスの法則、アンペールの法則、マックスウェルの方程式が 鮮やかな形で表現できます。 ∇(ナブラ)の正体もわかります。 |
| 物理と対称性 |
マックスウェルの方程式をよく見ると対称性があります。 物理の方程式と対称性を数学的な観点でみると 意外なつながりがあるという話です。 |
| マックスウェルの応力 |
電気力線を弾性体(ゴム)とみなして、力の伝わり方などを 説明した考え方です。 |
| 電場エネルギー | 電場が持つエネルギーの式を導いた話です。 |
| 磁場エネルギー |
磁場が持つエネルギーの式です。 手抜きの説明と、直流RL回路を使った説明を書きました。 |
| ポインティングベクトル |
電磁エネルギーの流れ「ポインティングベクトル」の話です。 電磁波でもエネルギー保存則が成り立つ話から ポインティングベクトルを導いています。 |
| 電気エネルギーは導線の外を伝わる |
導線の外を電気エネルギーが流れる話です。 私が誤解した事、その誤解を解いていく過程を紹介しながら 「目からウロコ」にたどり着いた話です。 |
| 物質中の電場 | 物質中の電場の話です。 分極の話をしながら、物質中の電場の話をします |
| 物質中の磁場 | 磁性の話をしながら、物質中の磁場の話をします |
| 物質中のマックスウェルの方程式 | 物質中でもマックスウェルの方程式が成り立つ話です。 |
| 導体に侵入する電磁波 |
導体に侵入する電磁波が減衰していく話です。 表皮効果と同じ「表皮の厚さ」が出てきます |
| 表皮効果 |
目的の表皮効果の話です。 マックスウェルの方程式を解きながら 交流電流の周波数を上げると、表面にしか電流が流れなくなる話です。 |