被告の藤村電気商会は「電気は物じゃないから、窃盗にはならない」と主張した。
システム奮闘記:その105
(2016年5月22日に掲載)
電気と法律
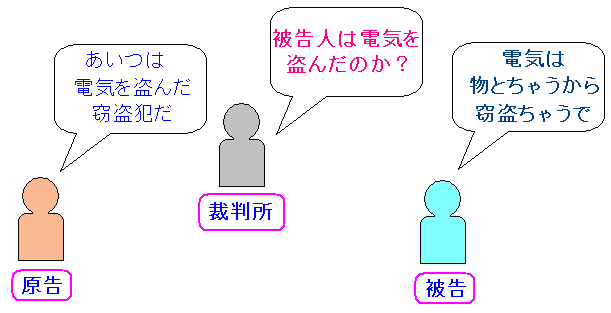
物理や数学の話だと疲れるので、気分転換として、電気と法律の話をします。 法律については「システム奮闘記:その101」(法学入門 IT技術者のための法律入門)をご覧ください。 明治時代の刑法で「他人の財物を盗んだら窃盗罪」というのがあった。 その時、電気は財物(物)かどうかが議論になった。 1882年、東京・銀座で日本初の電灯・アーク灯がともされた。 明治時代 電気の歴史年表(電気事業連合会) どんどん電気が普及していく中、1901年、横浜で事件が起こった。 藤村電気商会事件 なのだ。 藤村電気商会は無断で電気を引き込んでいたため、電力会社から電気泥棒で訴えられたのだ。 当時の刑法では窃盗罪とは 他人の財物の窃盗 になっていた。 そのため、以下のような争いになった。
| 電気泥棒(藤村電気商会事件) |
|---|
 |
|
原告の電力会社は「泥棒」と主張する一方で 被告の藤村電気商会は「電気は物じゃないから、窃盗にはならない」と主張した。 |
横浜地裁で有罪になったのだが、東京控訴院で行われた控訴審で逆転の無罪判決が出た。
判決理由は
電気は財物ではない
だった。
| 電気泥棒(藤村電気商会事件)の控訴審は無罪だった |
|---|
 |
|
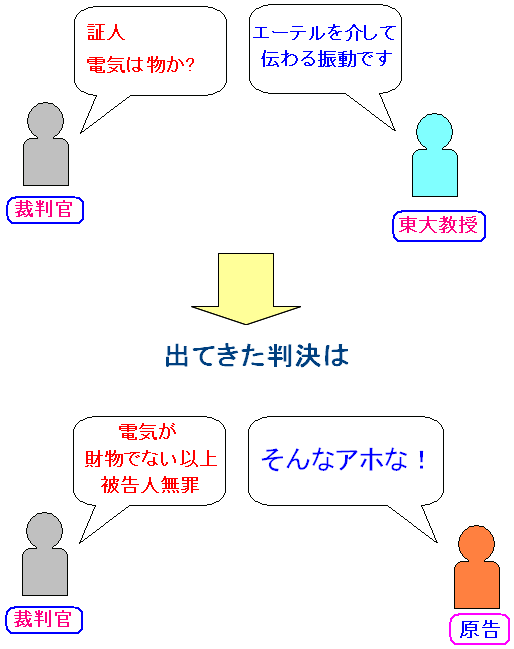
控訴審では東京帝国大学の物理学の教授が参考人として呼ばれた。 そして「電流はエーテルの作用に起因し、有体の物質的物件なりと云うを得ず」と証言したのだ。 つまり「電気は財物ではない」というのだ。 |
要するに 電磁波は物とちゃうで!! というのだ。 電気が物でない以上、財物には当たらないため、無罪になったのだ。電気は財物か?
日本の司法制度は罪刑法定主義だ。 法律に書いていない事は罪にならないのだ。 実際に、日本国憲法31条には次のように書かれている。
| 日本国憲法31条 |
|---|
|
何人も、法律の定める手続によらなければ、その生命若しくは自由を奪はれ 又はその他の刑罰を科せられない。 |
ところで電気泥棒が問題になったのは明治時代。 1890年に施行された明治憲法(大日本帝国憲法)の23条には以下のように書かれている。 憲法条文・重要文書 | 日本国憲法の誕生(国立国会図書館)
| 大日本帝国憲法・第23条 |
|---|
| 日本臣民ハ法律ニ依ルニ非スシテ逮捕監禁審問処罰ヲ受クルコトナシ |
|
(下手な現代語訳) 日本臣民は法律の根拠なく、逮捕・監禁・尋問・処罰を受ける事はない。 |
明治憲法も罪刑法定主義なのだ。 この事件が起こったのは明治憲法が施行された後なのだ。 そのため法律に書かれていない「財物以外の窃盗」は犯罪でないため 罪に問えなかったのだ。 電気を盗んで無罪になる。 これでは電力会社にとってはたまったものじゃないため上告になった。
| 電気泥棒(藤村電気商会事件)の大審院では逆転有罪 |
|---|
 |
|
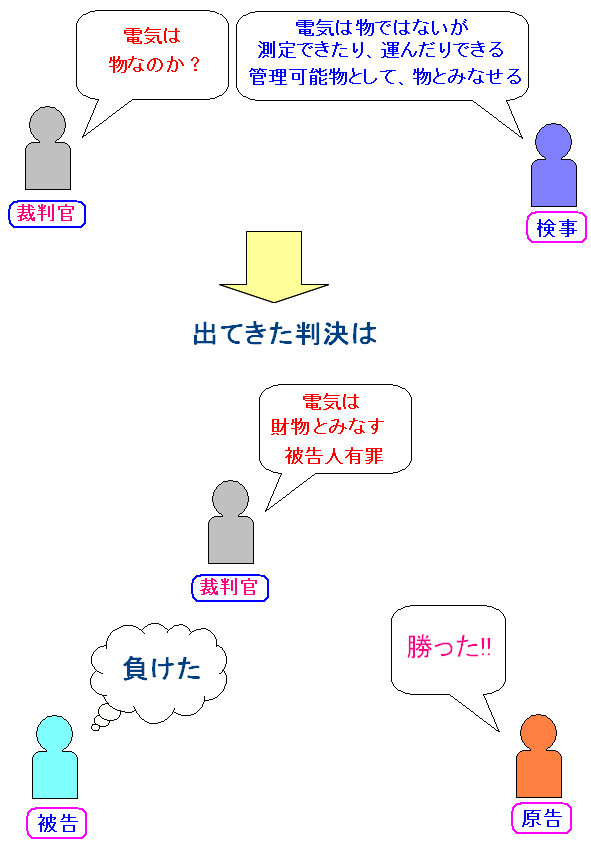
1903年、電気は物ではないが、測定可能で、導線で運搬ができるため 管理可能物として、物と同等の扱いができると解釈され、有罪判決になった。 |
判決の後、「電気を財物とみなす」の解釈について議論になった。
そして以下の2つの学説が出た。
拡大解釈説と類推解釈説
なのだ。
拡大解釈と類推解釈について説明すると以下のようになる。
| 拡大解釈と類推解釈について | |
|---|---|
| 拡大解釈 |
拡大解釈とは少し意味を広げて同質な物にする事だ。 例として「電車の中で飲食はしてはならない」だと 「ディーゼルやSL」も電車の中に含める事だ。 |
| 類推解釈 |
異質な物を同列にする事だ。 例として「電車の中で飲食はしてはならない」だと バスも船舶、飛行機も交通機関だから電車の中に含める事だ。 |
ところで判決で出た「電気を財物とみなす」の解釈については 以下の2つの学説が出たのだ。
| 「電気を財物とみなす」の解釈について | |
|---|---|
| 拡大解釈説 | 電気の管理可能な物なので 電気は物として扱えるので、財物とみなすという考え方 |
| 類推解釈説 |
電気と財物は異質だが、窃盗にあったのは変わらないので 財物と同じ物として扱う。 |
法律を知っている人なら、類推解釈の場合、問題になる。 刑法では類推解釈は禁止 という大原則がある。 罪刑法定主義だと、法に書いていない事は罪にならない。 だが、類推解釈すると、異質な物まで同じ物と解釈するので 法なき所に、勝手に法ができる という事になってしまう。 行政や司法が法を作ってしまうと、法律を作るのは立法府という三権分立にも反する。 この裁判の後、電気を財物に含めないと具合が悪いという事から 1907年(明治40年)に施工された現行刑法245条に この章の罪については、電気は、財物とみなす。 が入れられたのだ。 それ以来、よそ様の電気を無断で使うのは窃盗罪になったのだ。 そのためスマホのバッテリーが切れそうだからといって 無断で駅や公共施設、飲食店などにあるコンセントを使うと 窃盗罪 になってしまうし、実際に、窃盗罪で前科がついた例がある。 ところで財物かどうかで裁判になり、その後、法律ができた例は他にもある。 不動産泥棒だ。
| 不動産泥棒も裁判になった |
|---|
|
不動産が財物かどうかで問題になった。 そのため刑法に以下の条文が加えられた。 (刑法第235条の2) 他人の不動産を侵奪した者は、十年以下の懲役に処する。 |
日常生活だと・・・
勝手に人の○△を使うな!!
という事は、よくあるのだが、法律の観点で財物かどうかで考えると
安易に言えなくなるのだ。
他人の冷蔵庫を勝手に使った場合は、冷気泥棒になるのだろうか?
| 窃盗罪に問えない泥棒 |
|---|
|
よそ様の家の冷蔵庫に、勝手にジュースを入れて冷やした場合 冷気を盗んだ事になる。この場合、冷気を盗んだのは窃盗になるのだろうか。 冷蔵庫の無断使用。この辺りの話は面白いかもしれない。 |
法律については「システム奮闘記:その101」(法学入門 IT技術者のための法律入門)をご覧ください。 (電気泥棒に関する参考URL) 「はかる」世界: 「魂のはかり」から「電気のはかり」まで 法解釈学とは何か 刑法における財物の意義をめぐる論争を題材にして(愛知大学:CaLSプロジェクト:PPTファイル)
使用する単位系も法的根拠がある
電気泥棒の話の前が単位系の話だったので、関連づけた話を書く。 ワット(W)とかアンペール(A)など、日常使われているのだが 全国一律に計量するために、法律で決められているのだ。 計量法 計量単位令 計量単位令の中に、ワットやアンペールの定義が書かれているのだ。 日常生活などで使われる単位系は 全国一律の単位が使われるよう法的支援 がされているのだ。 ところで、効力のある法律としての、日本の最古の法律の話をする。 明治5年11月9日の太政官布告第337号の 日本の暦はグレゴリオ歴 なのだ。 太陰暦から太陽暦に変わったときだ。 現在、日本がグレゴリオ歴を採用しているのは法的根拠があるのだ。
| 明治5年太政官布告第337号 (一部抜粋) |
|---|
|
朕惟フニ我邦通行ノ暦タル太陰ノ朔望ヲ以テ月ヲ立テ太陽ノ躔度ニ合ス 故ニ二三年間必ス閏月ヲ置カサルヲ得ス置閏ノ前後時ニ季候ノ 早晩アリ終ニ推歩ノ差ヲ生スルニ至ル殊ニ中下段ニ掲ル所ノ如キハ 率子妄誕無稽ニ属シ人知ノ開達ヲ妨ルモノ少シトセス盖シ太陽暦ハ 太陽ノ躔度ニ従テ月ヲ立ツ日子多少ノ異アリト雖モ季候早晩ノ変ナク 四歳毎ニ一日ノ閏ヲ置キ七千年ノ後僅ニ一日ノ差ヲ生スルニ過キス之ヲ 太陰暦ニ比スレハ最モ精密ニシテ其便不便モ固リ論ヲ俟タサルナリ依テ 自今旧暦ヲ廃シ太陽暦ヲ用ヒ天下永世之ヲ遵行セシメン百官有司其レ斯旨ヲ体セヨ |
読む気が起こらへん!!
なのだ。
明治憲法も議会もなかった時の、太政官布告(明治政府の通達)が
法律として効力があるかどうかの議論出てくるだろう。(学説もあります)
現在でも、いくつかの太政官布告は有効とされている。
そして、死刑の方法が絞首刑なのは、太政官布告にあるからだ。
| 明治六年太政官布告第六十五号(絞罪器械図式) |
|---|
|
絞罪器械別紙図式ノ通改正相成候間各地方ニ於テ右図式ニ従ヒ製造可致事 (以下、省略) 法令データベースだと、絞首刑台の図が省略されているのだ。 |
だが、首吊り台の絵を載せているサイトがある。 絞首刑の執行方法は太政官布告が根拠法令だった(保坂展人のどこどこ日記) ところで明治憲法が施行された際、明治憲法に反しない法律や通達は有効とされた上 現行憲法でも、憲法に反しない物は、法律として認めているため、太政官布告は有効だというのだ。 法制執務コラム 「法律」ではない「法律」(参議員法制局) でも、あくまでも参議院法制局の解釈で、法的効力の有無を決めるのは、裁判所なのだ。
電磁気学入門の目次
| 電磁気学入門:目次 | |
|---|---|
| スカラーとベクトル | 簡単なスカラーとベクトルの話です。 ベクトルは方向と大きさを持つ量。方向という量持っているだけに注意が必要です。 |
| 静電気の発見からクーロンの法則 | 今でこそ当たり前の静電気や導体、絶縁体、電荷など どういう経緯で発見し、クーロンの法則まで至ったのかの話です。 |
| クーロン力、電場、近接作用 | 4つの力のうち、クーロン力の位置づけ 電荷が作り出す作用の電場。近接作用の話です。 |
| 微分、全微分、方向微分 | 簡単な微分、全微分、方向微分の話です。 ここをしっかり押さえないと、電磁気の数式の意味が わからなくなります。 |
| ベクトル解析 |
電磁気に必要なベクトル解析の話です。 勾配(grad)、2次元のグリーン定理 ストークスの定理の話です。 |
| 電位ポテンシャル | 電位ポテンシャルです。勾配と電場の関係を使って説明しています。 |
| 電気双極子 |
電気双極子の話です。 物質中で起こる分極を理解するのに必要です。 |
| ガウスの法則 | ガウスの法則の積分形、微分形の話です。 |
| ポアソンの方程式、ラプラス方程式 |
ポアソンの方程式、ラプラス方程式の話です。 単に電荷分布から電位を求めるだけの話にとどまらない 奥が深い分野です。ポテンシャル論、デルタ関数 グリーン関数、固有値問題について触れています。 |
| 静電場と渦なしの法則 |
静電場で、電荷を1周させた時の仕事はゼロ 微分形と微分形の渦なしの法則の話です。 |
| ビオサバールの法則 |
電気と磁場の関係の発見の話から ビオ・サバールの法則が導かれるまでの話です。 |
| 磁気双極子 |
磁気双極子の話で、回転電流になります。 物質中の磁場の話にも関連します。 |
| アンペールの法則 |
アンペールの法則の話です。 積分形・微分形だけでなく、閉回路に流れる電流が作る 磁気双極子の話なども書いています。 |
| ローレンツ力 |
磁場中を移動する電荷にかかる力(ローレンツ力)の話です。 ローレンツ力は相対性理論が絡んでいる事も紹介しています。 |
| ファラデーの誘導起電力の法則 | ファラデーの誘導起電力の話です。 |
| うず電流を使った簡単な物理実験 | 電力計に使われるアラゴの円盤。 そしてIH調理器で熱するために発生させる、うず電流は レンツの法則から電流が発生する原理を応用した物だ。 アラゴの円盤の実験と、IH調理器を使った実験です。 気分転換で読んでください。 |
| ベクトルポテンシャル |
わかりにくいベクトルポテンシャルの話です。 電位は電荷が作る電気のポテンシャルだが ベクトルポテンシャルは電流が作る磁場のポテンシャルの話です。 |
| オームの法則の微分形 | 微小領域でのオームの法則の話です。 |
| マックスウェルの方程式 |
4つのマックスウェルの方程式を書いています。 電場と磁場の変化を図にする事で rotの回転の意味も理解できます。 |
| ゲージ変換 |
ゲージ(gauge)は物差しの意味です。 マックスウェルの方程式をE(電場)とB(磁場)の関係式から φ(電位ポテンシャル)とA(ベクトルポテンシャル)の関係式に 書き換える際、ゲージ変換が使われます。 ゲージ変換の役目を書きました。 |
| 電磁波 |
マックスウェルの方程式から電波が伝わる様子を 視覚的に見てみる話です。 |
| 回転のrotはベクトルの微分 |
ベクトル解析や渦なしの法則で出てくるrotは ベクトルの微分という話です。 |
| 電磁気学の単位系 | 電磁気学の単位系の話です。 物理量の単位系の指数を見る次元解析 電磁気学の歴史と単位系の変遷について触れました。 |
| 電気泥棒:電気と法律の話 |
電気は物体なのか、無形物なのか。 明治時代に、電気を無断で使った場合、物か、そうでないかで 窃盗罪になるかどうかが裁判で問われました。 ちょっとした科学と法律の話です。気分転換で読んでください。 |
| 数ベクトルと基底ベクトル | ベクトルの話です。 矢印だけがベクトルでない事。 数ベクトルと基底ベクトルの違いの話です。 多様体、反変・共変ベクトルを理解するのに必要です |
| 多様体 | 空間を一般化した話です。 ▽(ナブラ)の正体に迫まります |
| 外積代数 |
外積、テンソルについて書いています。 極性ベクトル、軸性ベクトル 外積は行列で、ベクトルは見せかけの姿だった話です。 |
| ベクトルの双対関係 |
反変ベクトル、共変ベクトル、双対関係 ベクトル解析、外積代数の話 外積、テンソルについて書いています。 |
| ローレンツ力と相対性理論 |
磁場は電場の相対論的効果だった話です。 ローレンツ力を使って、導線が作る磁場を使って説明です。 |
| 微分形式 |
多様体の話の続きです。 座標に依存しない形での関数やベクトルの微分の話です。 ガウスの法則、アンペールの法則、マックスウェルの方程式が 鮮やかな形で表現できます。 ∇(ナブラ)の正体もわかります。 |
| 物理と対称性 |
マックスウェルの方程式をよく見ると対称性があります。 物理の方程式と対称性を数学的な観点でみると 意外なつながりがあるという話です。 |
| マックスウェルの応力 |
電気力線を弾性体(ゴム)とみなして、力の伝わり方などを 説明した考え方です。 |
| 電場エネルギー | 電場が持つエネルギーの式を導いた話です。 |
| 磁場エネルギー |
磁場が持つエネルギーの式です。 手抜きの説明と、直流RL回路を使った説明を書きました。 |
| ポインティングベクトル |
電磁エネルギーの流れ「ポインティングベクトル」の話です。 電磁波でもエネルギー保存則が成り立つ話から ポインティングベクトルを導いています。 |
| 電気エネルギーは導線の外を伝わる |
導線の外を電気エネルギーが流れる話です。 私が誤解した事、その誤解を解いていく過程を紹介しながら 「目からウロコ」にたどり着いた話です。 |
| 物質中の電場 | 物質中の電場の話です。 分極の話をしながら、物質中の電場の話をします |
| 物質中の磁場 | 磁性の話をしながら、物質中の磁場の話をします |
| 物質中のマックスウェルの方程式 | 物質中でもマックスウェルの方程式が成り立つ話です。 |
| 導体に侵入する電磁波 |
導体に侵入する電磁波が減衰していく話です。 表皮効果と同じ「表皮の厚さ」が出てきます |
| 表皮効果 |
目的の表皮効果の話です。 マックスウェルの方程式を解きながら 交流電流の周波数を上げると、表面にしか電流が流れなくなる話です。 |