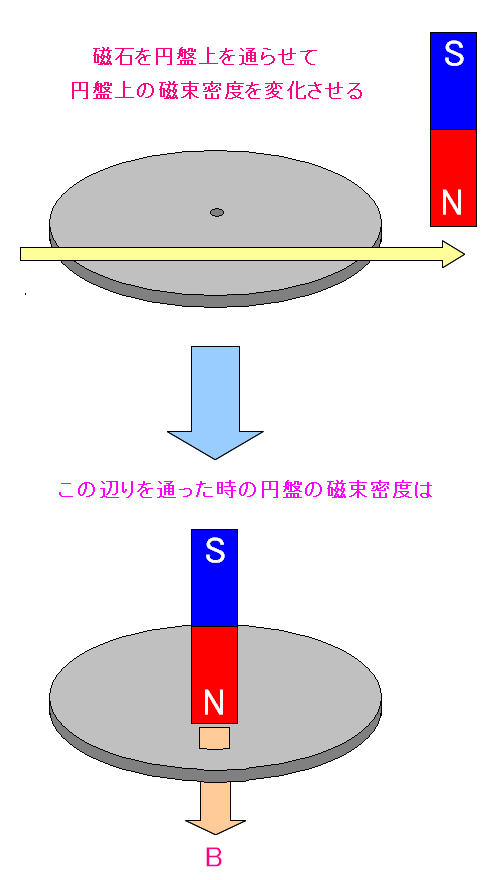
円盤上を通過する際、磁石から円盤に向かって磁束密度が伸びているのだ。
システム奮闘記:その105
(2016年5月22日に掲載)
アラゴの円盤の実験
ローレンツ力とファラデーの誘導起電力の法則の復習にもってこいの実験だ。 渦電流とは、金属の板に磁場を変化させると 板内部で渦を巻いた電流が発生するのだ。 身近な活用例としては、アラゴの円盤で、家庭の電力計に使われている。 【アラゴの円板から積算電力量計、誘導モータへ】(磁石とマグネットのNeoMag -NeoMag通信バックナンバー)
| アラゴの円盤 |
|---|
 |
|
アルミなどの円盤の上を、磁石が通過すると考える。 円盤上を通過する際、磁石から円盤に向かって磁束密度が伸びているのだ。 |
磁石が円盤上を通過する際、円盤上で、うず電流が発生する。
| 磁石が円盤上を通過する際、円盤上で、うず電流が発生する |
|---|
 |
|
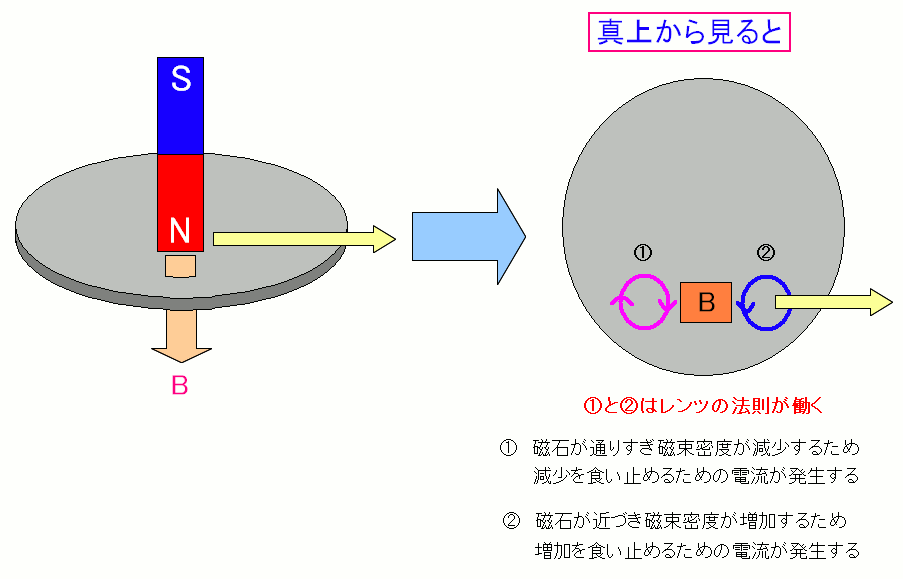
磁石を近づけると、磁束密度が増加するため レンツの法則により、電流が発生し、磁束密度が増加しないように働く。 磁石が通過した所では、磁束密度が減少するため レンツの法則により、電流が発生し、磁束密度が減少しないように働く。 |
レンツの法則が働く結果、以下のことが起こる。
| レンツの法則によって磁石の下を通過する電流が発生する |
|---|
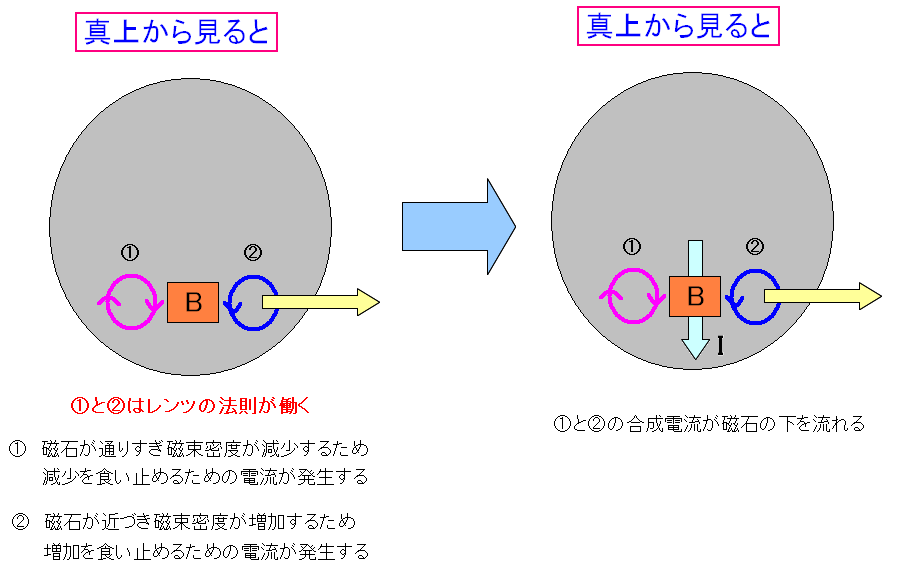 |
| レンツの法則で発生した(1)と(2)の電流が合成した形になる。 |
合成した電流と磁束密度は垂直になる。
この時・・・
ローレンツ力が働く
のだ。
| 円盤にローレンツ力が働く |
|---|
 |
|
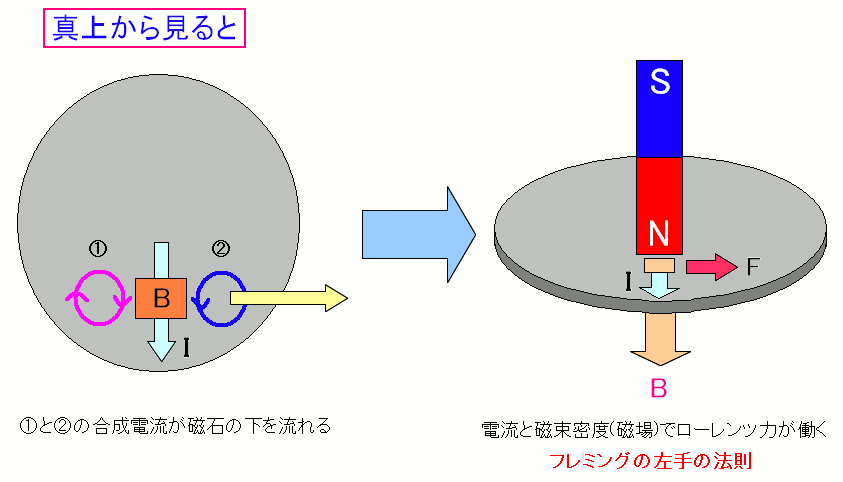
磁石が発する磁束密度と、レンツの法則によって発生した電流により ローレンツ力が働く。その結果、磁石を追いかける方向に力が働くのだ。 |
この物理現象を・・・
アラゴの円盤
と呼ぶのだ。
アラゴの円盤の原理がわかった所で、100金で買える物と家にあるもので
アラゴの円盤の実験をしてみる事にした。
| アルミ箔と磁石を100金で買ってきた |
|---|
 |
|
アルミ箔は100金で買わなくても家庭にもある。 円盤状にアルミ箔を切った。 |
そして円盤状にしたアルミ箔を、水を張った洗面器の上に浮かべる。
| 水に浮かせたアルミ箔の上を磁石で回す |
|---|
 |
|
原理的にはアルミ箔も動き出すはずだったのだが どうやら実験はうまくいなかった。磁石が弱かったかもしれない・・・。 |
IH調理器を使った実験
他の実験がないか探してみると、IH調理器を使った実験を発見した。 おもしろ実験と自由研究「電磁調理器でUFOを飛ばそう!の改良版」 IH調理器を使った理科学習(京都教育大学:pdf) まずはIH調理器の原理から説明する。(本の丸写しだが・・・) 「第15回 今夜は鍋にしましょうか? ? 火を使わないIH調理器の仕組み?|テクの雑学|TDK Techno Magazine」の丸写しだが・・・。
| IH調理器 |
|---|
 |
|
おなじみになったIH調理器 火を使わないため火事の心配が少ないと言われる。 ただ鍋の材質によって使えない場合があるので、ガスコンロと一長一短の所もある。 |
IH調理器の仕組みは以下の通りだ。(完全に受け売り)
| IH調理器の仕組み |
|---|
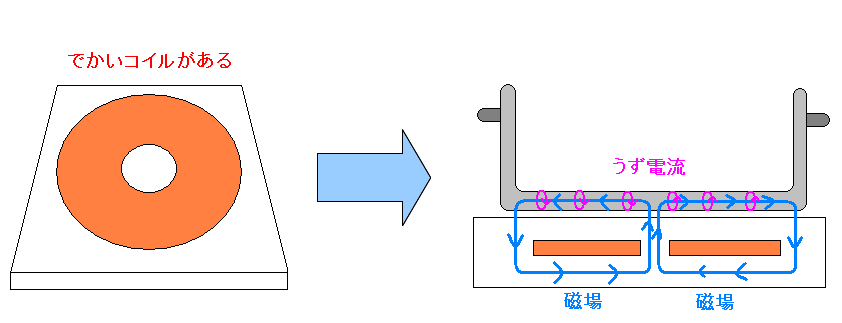 |
|
中に大きなコイルがあり、真ん中に穴があいている 電源を入れると、コイルから磁場が発生する。 鍋底の金属部分で、うず電流が発生する。 この、うず電流が鍋の抵抗によって、熱エネルギーになり その熱が過熱に使われる。 |
さて、IH調理器の上にアルミ箔を乗せるとどうなるのか?
| IH調理器の上にアルミ箔を乗せる |
|---|
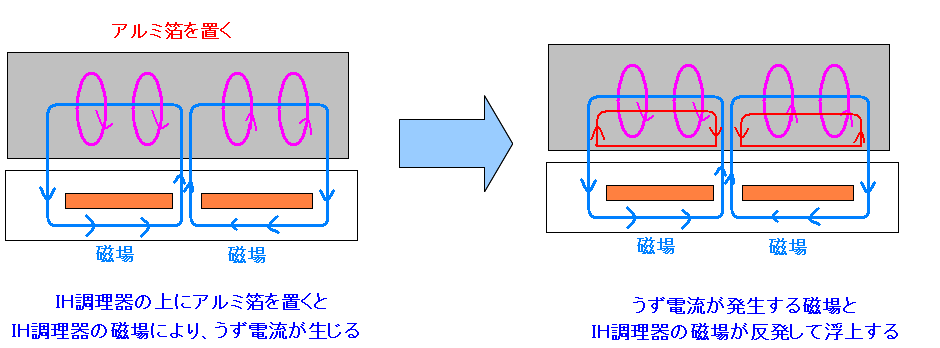 |
|
鍋と同様、アルミ箔内部でも、うず電流が生じる。 レンツの法則より、IH調理器が発生する磁場とは反対向きに うず電流が磁場を発生させる。 その時、磁場が反発しあって、アルミ箔が浮上するのだ。 (突っ込まないでね) 絵を描く都合上、分厚いアルミ箔になってしまった。 でも、許してチョンマゲなのだ。 |
早速、ドーナツ状に切ったアルミ箔をIH調理器に乗せてみる。
| ドーナツ状に切ったアルミ箔をIH調理器に乗せてみる |
|---|
 |
IH調理器の真ん中に金属のコップを置く。
| IH調理器の真ん中に金属のコップを置く |
|---|
 |
| 物の有無や材質を見るセンサーを騙すためだ。 |
早速、電源を入れてみる。
| 電源を入れるとアルミ箔が浮上し始める |
|---|
 |
|
電源を入れるとアルミ箔が浮上し始めるのだが これでは見にくい。 |
でも、しっかりとアルミ箔が浮上してくれた。
| しっかりとアルミ箔が浮上してくれた |
|---|
 |
| まさにUFOという感じだ。 |
物理の世界を数式ばかりだと退屈だし、しんどくなる。 やはり・・・ 物理は実験しないとオモロナイ!! なのだ。 あとは手軽な実験を思いつくかどうかで、 物理の理解度がわかってしまう そのため実験は大事だと思った。
電磁気学入門の目次
| 電磁気学入門:目次 | |
|---|---|
| スカラーとベクトル | 簡単なスカラーとベクトルの話です。 ベクトルは方向と大きさを持つ量。方向という量持っているだけに注意が必要です。 |
| 静電気の発見からクーロンの法則 | 今でこそ当たり前の静電気や導体、絶縁体、電荷など どういう経緯で発見し、クーロンの法則まで至ったのかの話です。 |
| クーロン力、電場、近接作用 | 4つの力のうち、クーロン力の位置づけ 電荷が作り出す作用の電場。近接作用の話です。 |
| 微分、全微分、方向微分 | 簡単な微分、全微分、方向微分の話です。 ここをしっかり押さえないと、電磁気の数式の意味が わからなくなります。 |
| ベクトル解析 |
電磁気に必要なベクトル解析の話です。 勾配(grad)、2次元のグリーン定理 ストークスの定理の話です。 |
| 電位ポテンシャル | 電位ポテンシャルです。勾配と電場の関係を使って説明しています。 |
| 電気双極子 |
電気双極子の話です。 物質中で起こる分極を理解するのに必要です。 |
| ガウスの法則 | ガウスの法則の積分形、微分形の話です。 |
| ポアソンの方程式、ラプラス方程式 |
ポアソンの方程式、ラプラス方程式の話です。 単に電荷分布から電位を求めるだけの話にとどまらない 奥が深い分野です。ポテンシャル論、デルタ関数 グリーン関数、固有値問題について触れています。 |
| 静電場と渦なしの法則 |
静電場で、電荷を1周させた時の仕事はゼロ 微分形と微分形の渦なしの法則の話です。 |
| ビオサバールの法則 |
電気と磁場の関係の発見の話から ビオ・サバールの法則が導かれるまでの話です。 |
| 磁気双極子 |
磁気双極子の話で、回転電流になります。 物質中の磁場の話にも関連します。 |
| アンペールの法則 |
アンペールの法則の話です。 積分形・微分形だけでなく、閉回路に流れる電流が作る 磁気双極子の話なども書いています。 |
| ローレンツ力 |
磁場中を移動する電荷にかかる力(ローレンツ力)の話です。 ローレンツ力は相対性理論が絡んでいる事も紹介しています。 |
| ファラデーの誘導起電力の法則 | ファラデーの誘導起電力の話です。 |
| うず電流を使った簡単な物理実験 | 電力計に使われるアラゴの円盤。 そしてIH調理器で熱するために発生させる、うず電流は レンツの法則から電流が発生する原理を応用した物だ。 アラゴの円盤の実験と、IH調理器を使った実験です。 気分転換で読んでください。 |
| ベクトルポテンシャル |
わかりにくいベクトルポテンシャルの話です。 電位は電荷が作る電気のポテンシャルだが ベクトルポテンシャルは電流が作る磁場のポテンシャルの話です。 |
| オームの法則の微分形 | 微小領域でのオームの法則の話です。 |
| マックスウェルの方程式 |
4つのマックスウェルの方程式を書いています。 電場と磁場の変化を図にする事で rotの回転の意味も理解できます。 |
| ゲージ変換 |
ゲージ(gauge)は物差しの意味です。 マックスウェルの方程式をE(電場)とB(磁場)の関係式から φ(電位ポテンシャル)とA(ベクトルポテンシャル)の関係式に 書き換える際、ゲージ変換が使われます。 ゲージ変換の役目を書きました。 |
| 電磁波 |
マックスウェルの方程式から電波が伝わる様子を 視覚的に見てみる話です。 |
| 回転のrotはベクトルの微分 |
ベクトル解析や渦なしの法則で出てくるrotは ベクトルの微分という話です。 |
| 電磁気学の単位系 | 電磁気学の単位系の話です。 物理量の単位系の指数を見る次元解析 電磁気学の歴史と単位系の変遷について触れました。 |
| 電気泥棒:電気と法律の話 |
電気は物体なのか、無形物なのか。 明治時代に、電気を無断で使った場合、物か、そうでないかで 窃盗罪になるかどうかが裁判で問われました。 ちょっとした科学と法律の話です。気分転換で読んでください。 |
| 数ベクトルと基底ベクトル | ベクトルの話です。 矢印だけがベクトルでない事。 数ベクトルと基底ベクトルの違いの話です。 多様体、反変・共変ベクトルを理解するのに必要です |
| 多様体 | 空間を一般化した話です。 ▽(ナブラ)の正体に迫まります |
| 外積代数 |
外積、テンソルについて書いています。 極性ベクトル、軸性ベクトル 外積は行列で、ベクトルは見せかけの姿だった話です。 |
| ベクトルの双対関係 |
反変ベクトル、共変ベクトル、双対関係 ベクトル解析、外積代数の話 外積、テンソルについて書いています。 |
| ローレンツ力と相対性理論 |
磁場は電場の相対論的効果だった話です。 ローレンツ力を使って、導線が作る磁場を使って説明です。 |
| 微分形式 |
多様体の話の続きです。 座標に依存しない形での関数やベクトルの微分の話です。 ガウスの法則、アンペールの法則、マックスウェルの方程式が 鮮やかな形で表現できます。 ∇(ナブラ)の正体もわかります。 |
| 物理と対称性 |
マックスウェルの方程式をよく見ると対称性があります。 物理の方程式と対称性を数学的な観点でみると 意外なつながりがあるという話です。 |
| マックスウェルの応力 |
電気力線を弾性体(ゴム)とみなして、力の伝わり方などを 説明した考え方です。 |
| 電場エネルギー | 電場が持つエネルギーの式を導いた話です。 |
| 磁場エネルギー |
磁場が持つエネルギーの式です。 手抜きの説明と、直流RL回路を使った説明を書きました。 |
| ポインティングベクトル |
電磁エネルギーの流れ「ポインティングベクトル」の話です。 電磁波でもエネルギー保存則が成り立つ話から ポインティングベクトルを導いています。 |
| 電気エネルギーは導線の外を伝わる |
導線の外を電気エネルギーが流れる話です。 私が誤解した事、その誤解を解いていく過程を紹介しながら 「目からウロコ」にたどり着いた話です。 |
| 物質中の電場 | 物質中の電場の話です。 分極の話をしながら、物質中の電場の話をします |
| 物質中の磁場 | 磁性の話をしながら、物質中の磁場の話をします |
| 物質中のマックスウェルの方程式 | 物質中でもマックスウェルの方程式が成り立つ話です。 |
| 導体に侵入する電磁波 |
導体に侵入する電磁波が減衰していく話です。 表皮効果と同じ「表皮の厚さ」が出てきます |
| 表皮効果 |
目的の表皮効果の話です。 マックスウェルの方程式を解きながら 交流電流の周波数を上げると、表面にしか電流が流れなくなる話です。 |