システム奮闘記：その105

微分形式

(2016年5月22日に掲載)

微分形式と外積代数

　微分形式とは、多様体上の関数の微分の話だ。
　座標系に依存しない形で表現する。

　でも、多様体のすぐ後に微分形式の話を書かなかったのは

　外積代数の知識が必要

　なのだ。

計算方法を知っているだけでも良いかもしれないが
微分形式の場合、外積(クロス積)の計算方法を知っていれば外積代数や多様体の知識がなくても計算はできる。だが、微分形式の計算法だけ知っていても裏側にある数学が見えていないと理解はできない。少しでも多様体をかじった上で微分形式に触れた方が良いと思ったりする。


　多様体上では、座標が決められていない。
　言い換えると、微分も速度ベクトルも勾配も

　座標に依存しない表現

　と表わすのだ。


　ところで多様体上で、正規直交座標系が適用できる領域は
以下の基底ベクトルで表現できる。

多様体上で、正規直交座標系が適用できる領域での基底ベクトル

多様体上で、直交座標系が使える場合の基底ベクトルなのだ。


　多様体の場合、関数を微分した際、微分の表現は

　双対ベクトルで表現

　をしていたのだ。

基底ベクトルと双対関係のベクトル

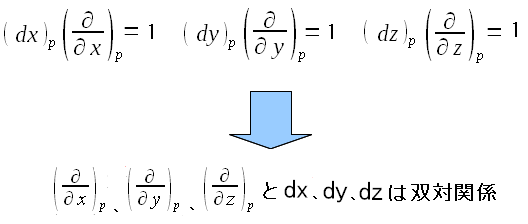双対関係のベクトルを、基底ベクトルとして関数の微分を表現したのだ。


　双対関係のベクトルを基底ベクトルとして扱えるので、以下の直交座標系と
基底ベクトルを使う。

　多様体上の関数の微分表現は

　双対ベクトルを使って表現する決まり

　というわけなのだ。


　そこで、ここからは多様体の話で出てきた直交座標系の基底ベクトル(微分演算子)ではなく
その双対ベクトルを基底ベクトルとして扱うのだ。

直交座標系と基底ベクトルを使う

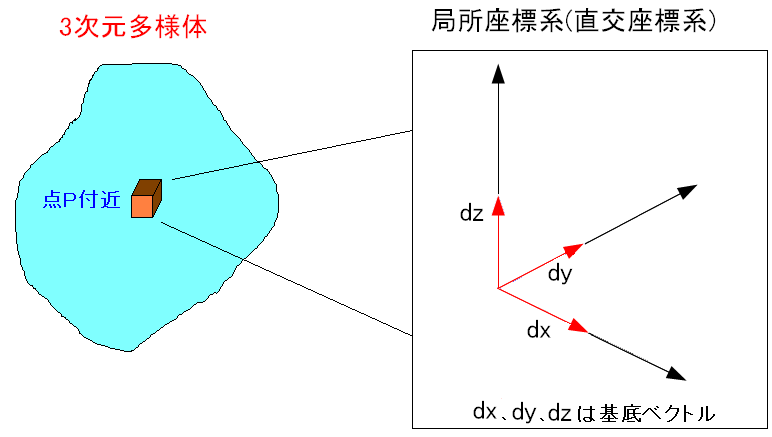dx,dy,dzを基底ベクトルとして使うのだ。


　まずは多様体上の関数から見ていく。

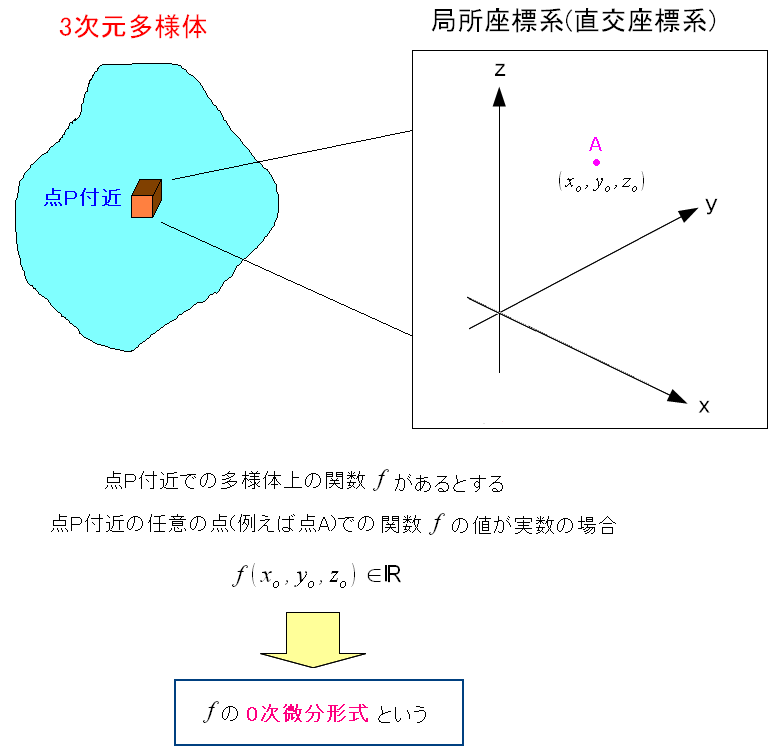
多様体上の関数は0次微分形式

多様体上の関数に座標を入れると、実数が出てくる。この時点では、微分をしていないため、0次微分形式と呼ぶのだ。


　そして多様体上の関数fを微分(全微分)した時の形式を
1次微分形式という。

関数fを微分(全微分)した時の形式を1次微分形式

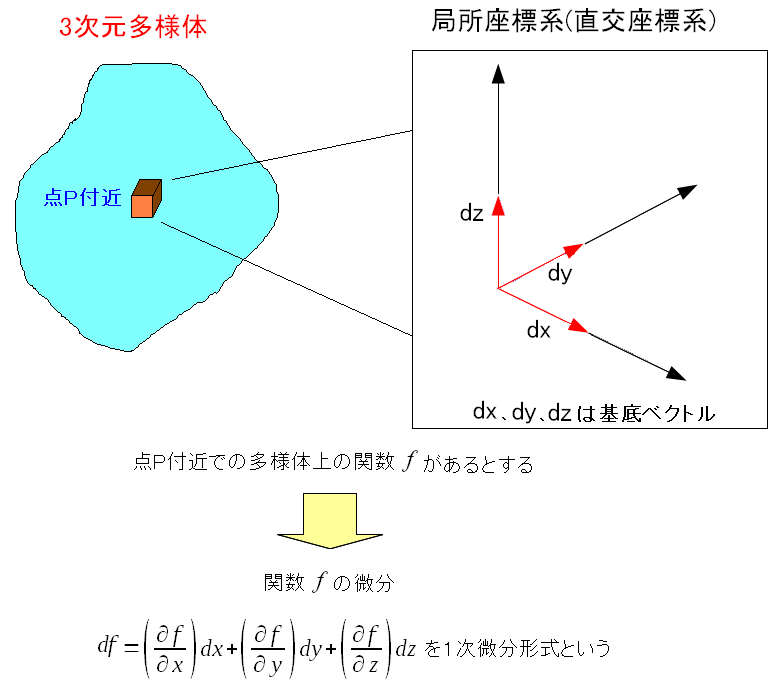色々な所で見た全微分は、1次微分形式だったのだ。


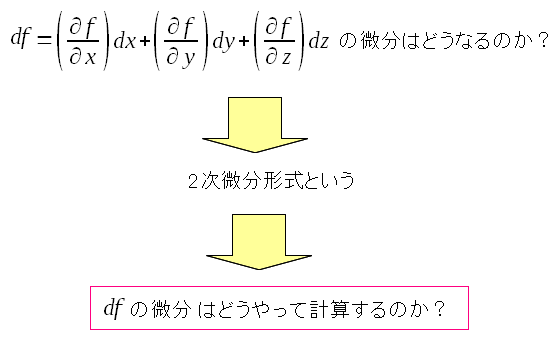
　さて、1次微分形式の関数を、さらに微分したらどうなるのか?

1次微分形式の関数を、さらに微分したら

2次微分形式になるのだが、どういう形になるかは数学の定義を見ていく必要がある。


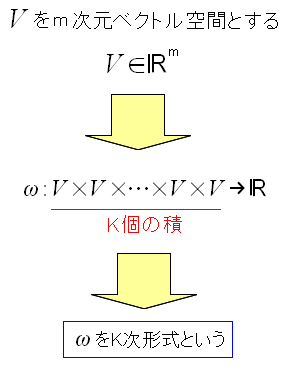
　まずはm次元ベクトル空間(V)を考える。

K次形式とはK個のテンソル積

m次元ベクトル空間(V)をK個用意し、それらのテンソル積を K次形式という。まだ「微分」という枕詞は付かない。


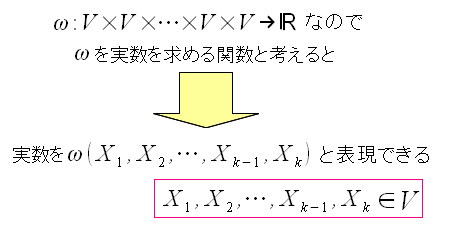
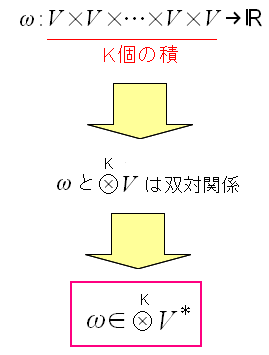
　K次形式を実数にする関数ωを考える。
　K次形式を実数にするので、内積の相手と呼んでも良い。

K次形式を実数にする関数ω

K次形式は、テンソル積なので、どういう量なのか想像はできない。ただ、ωによって実数になる事だけがわかっている。


　ベクトルの内積をとって実数になるのは、
テンソル積との双対関係とも言える。

ωはテンソル積とは双対関係

多様体上の関数の微分を求めた際に、関数の微分形を構成するベクトルが局所座標系のベクトルと双対関係だった。なんとなく、似ているように思えてきた。


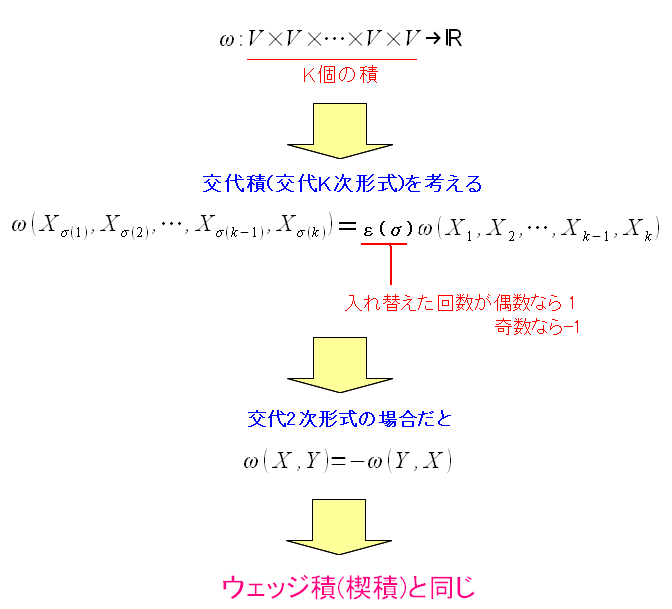
　テンソル積は、テンソル積でも、交代積を使う。
　外積(ウェッジ積やクロス積)の計算に似てきた。

テンソル積でも、交代積を使う

ウェッジ積(楔積)では、積の順序を変えると、符号が変わった。それと同じなのだ。ただし、K次テンソルなので、複数回、積の順序を交換できるため偶数なら1、奇数なら-1という規則がある。


　そして交代積だけを取り出す。
　K次微分形式が定義できたのだ。

「K次微分形式」の定義

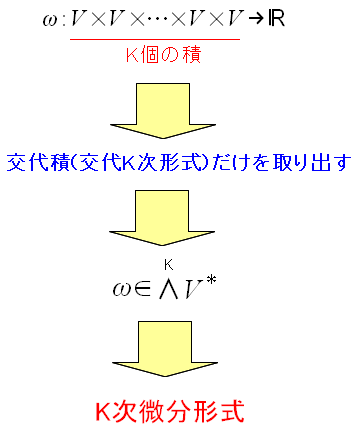K次のテンソルで、交代積の事を「K次微分形式」というのだ。


　だが・・・

　なんだかよくわからへん

　つまり言い換えると

　全くわかってへん

　なのだ。

　テンソルが絡んでくると、私の頭では想像できない世界のため
数式の丸写しになってくる。

　だが、使う範囲といえばK次微分形式どころか・・・

　3次微分形式まで

　なのだ。


　そこで計算方法を見ていく事にした。


微分形式の計算方法

　習うより慣れろと学問の世界でいったら、怒られるかもしれない。
　でも、イマイチわからん時(全くわからん)は、手を動かすという方法もある。


　話を簡単にするため、まずはベクトル積の2階のテンソルで考える。
　外積代数で出てきたウェッジ積の話になり、わかりやすくなる。

ウェッジ積を考える

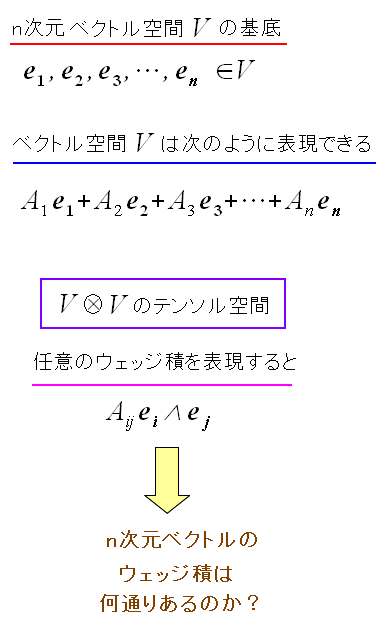n次元ベクトルのウェッジ積の場合、基底は何通りできるのか考えてみる。


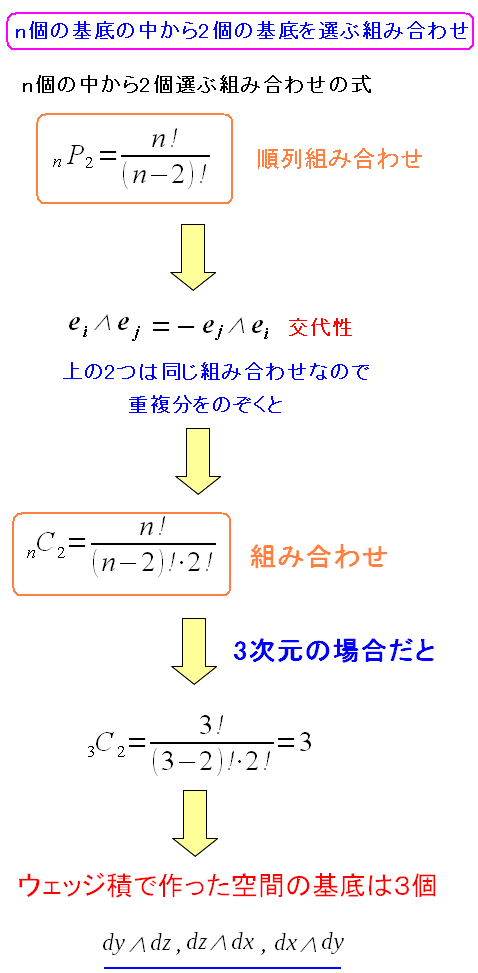
　基底の数だが、順列組み合わせを使えば解ける。

基底の数は、順列組み合わせを使えば解ける

ウェッジ積は交代積だ。そのため「dx∧dy」と「-dy∧dx」という同じ基底がでてきたり「dx∧dx=0」なので、それを省くようにする 3次元ベクトルの場合だと、ウェッジ積で作った基底は3つになる。


　次にベクトルを3つかけあわせた、3階のテンソル(ウェッジ積)の場合を見てみる。

3階のテンソル(ウェッジ積)の場合

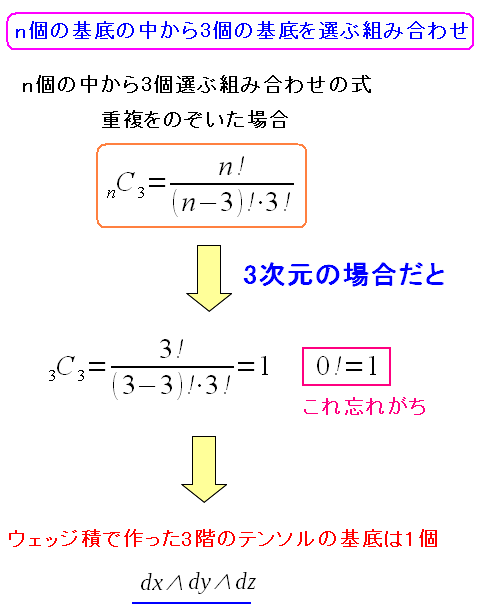ウェッジ積の性質を利用すれば、基底は1個になってしまう。


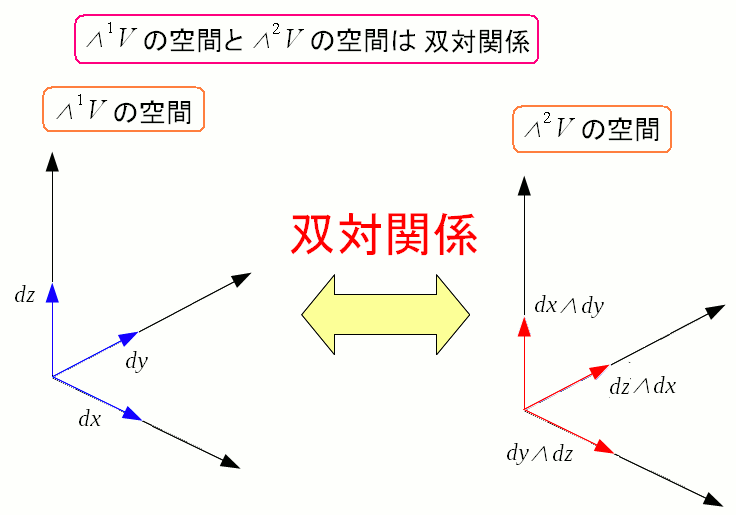
　そして外積代数の話では、ウェッジ積(2階のテンソル)にホッジスターをつけると
1階のテンソル(ベクトル)との対応関係ができる話をした。

　まさにそれが出てきた。

1階のテンソルと2階のテンソルの対応づけ

2階のテンソルを、1階のテンソル(ベクトル)と対応させる事で、双対関係になれる。ベクトルの双対関係でも触れた話だが 1階のテンソルと、2階のテンソルのウェッジ積は自由度1の3階のテンソルになるのだ。


　1階のテンソルと2階のテンソルが双対関係である事はわかった。

　そして・・・

　3階のテンソルはスカラーと対応づけできる

　のだ。


　そのため以下の表にまとめる事ができるのだ。

微分形式
0次微分形式	スカラー
1次微分形式	ｄｘ、ｄｙ、ｄｚを基底とするベクトルで表現される。
2次微分形式	dy∧dz、dz∧dx、dx∧dyを基底とする2階のテンソル。ただ基底が3つしかないので、1階のテンソル(ベクトル)との対応が可能なため 1次形式の双対関係になれる。
3次微分形式	dx∧dy∧dzを基底とする3階のテンソル。ただ、基底が1つしかないため、スカラーとの対応関係が可能。


　実際に、微分形式がどういう物なのか、具体的に見ていく事にした。

0次微分形式から2次微分形式

0次微分形式は、多様体上の関数の値でスカラーになる。
微分して1次微分形式(全微分)が出てくる。
この時に出てきたベクトルは極性ベクトルになる。

ここからの微分方法が大事になってくる。
1次微分形式の係数は関数になっている。
計算規則では、この関数を全微分するようになっている。
関数を全微分すると1次微分形式になるので、それと基底とのウェッジ積になる。

でてきたのは2次微分形式という。基底は3つなのでベクトルと対応づけできるのだ。
この時、でてくるのは軸性ベクトルなのだ。
そして、よく見ると形が回転のrotなのだ。


　この時・・・

　回転のrotは極性ベクトルの微分!!

　とハッキリした形で見えるのだ。
　ベクトル解析の段階では、わかりにくい話が、微分形式を使うと、鮮やかになる。


　2次微分形式から3次微分形式を計算してみる。

2次微分形式から3次微分形式

2次微分形式から3次微分形式にすると、基底が1個の物が出てくる。スカラーとの対応関係が可能なのだ。よく見ると、湧き出しのdivの形になっている。


　この時・・・

　湧き出しのdivは軸性ベクトルの微分!!

　とハッキリした形で見えるのだ。
　ベクトル解析の段階では、わかりにくい話が、微分形式を使うと、鮮やかになる。

　あまりにも鮮やかすぎて、驚くしかない。

　微分形式を知らないで、rotやdivを見ても、ベクトルの微分と気づかない上
言葉として知っていても、納得しにくい物になる。


閉形式と完全微分形

　そして任意の微分形式を2回微分するとゼロになるのだ。

微分形式を2回微分するとゼロになる

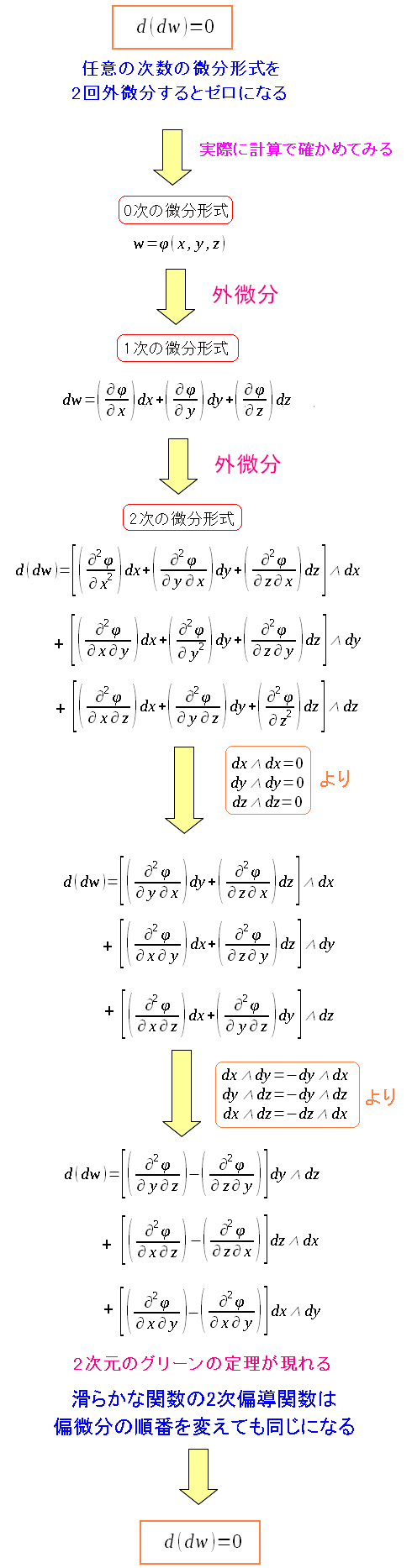確かに計算すればゼロになる。これだけだと、何に当てはまるのかが見えてこない。


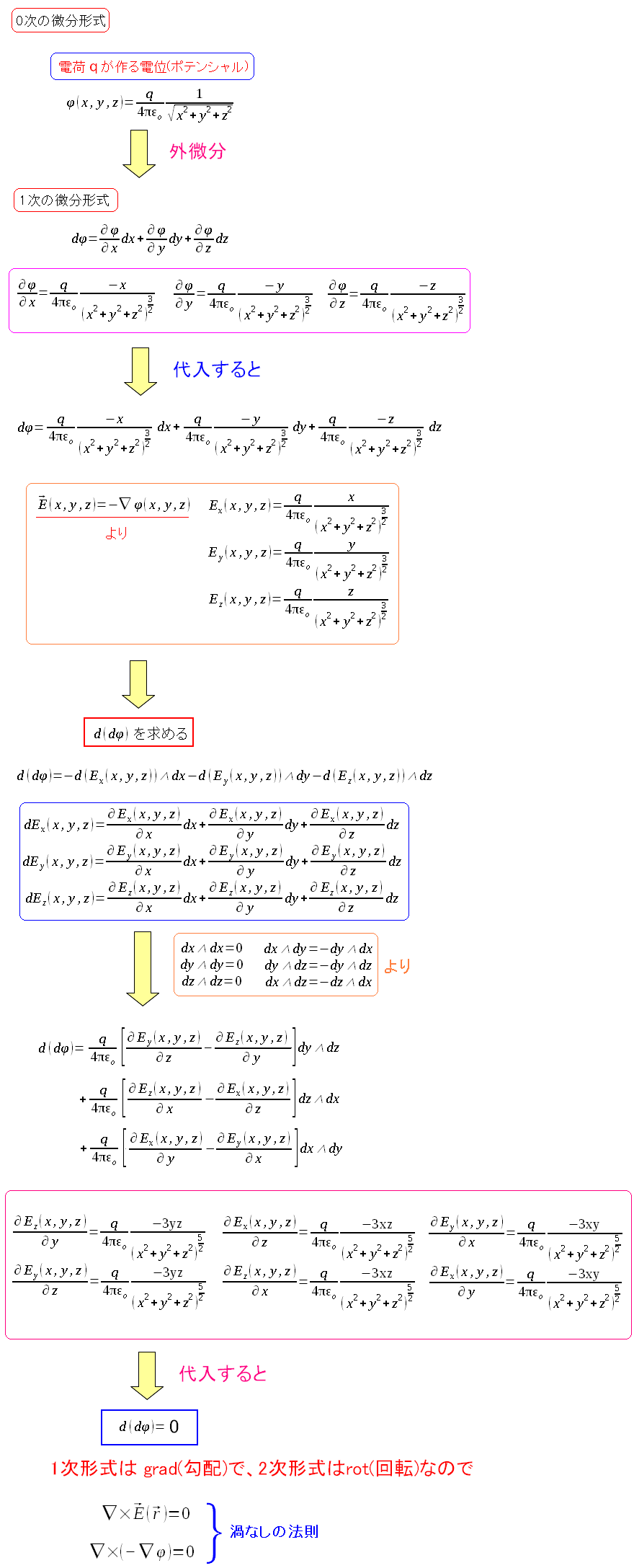
　だが、具体例があった。
　点電荷が作る電位ポテンシャルだ。

点電荷が作る電位ポテンシャル。2回微分するとゼロになる

静電場による渦なしの法則が出てきた。不通に計算すると大変だが、微分形式で考えると一発だ。鮮やかだ。


　渦なしの法則が、こんなにスッキリした形で表現できたとは想像もつかない。


　次に静磁場で見てみる。

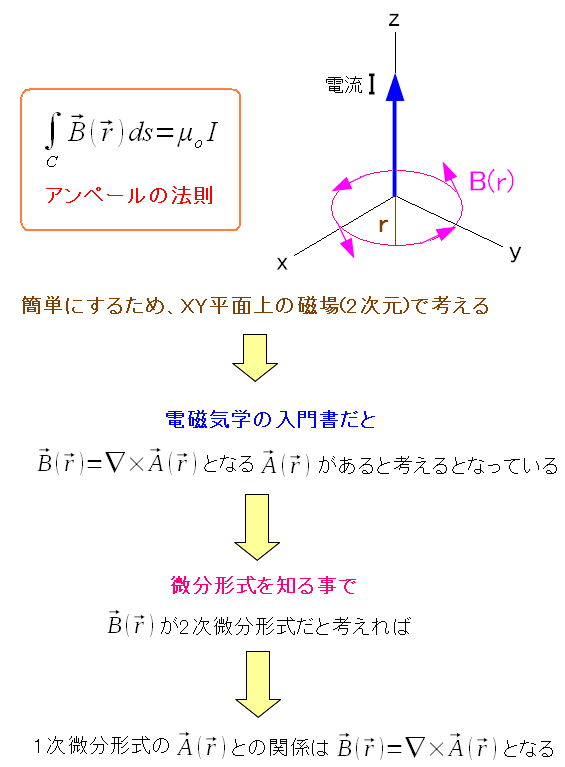
微分形式と、磁束密度とベクトルポテンシャルの関係

最初、磁束密度とベクトルポテンシャルの関係を書いた際
静磁場では∇・B=0になるので、∇・(▽×A)=0となるベクトルAが存在する。
B=▽×AとなるベクトルAを、ベクトルポテンシャルと書いた。

微分形式で見ると、1次微分形式であるベクトルポテンシャルを
微分したのが、2次微分形式の磁束密度(磁場)のベクトルだったのだ。


　そして静磁場中の湧き出しの法則を、微分形式を使ってみてみる。

静磁場中の湧き出しの法則を、微分形式を使ってみてみる

計算すると、めんどうだが、微分形式だと鮮やかだ。ベクトル解析の公式が面白いほど簡単に出てくる。


　微分形式を知ると

　物理の計算が不要という錯覚を起こす

　のだ。　

ポアンカレの補題

　ところで微分形式には閉形式と完全微分形がある。

閉形式と完全微分形

ある微分形式ωを微分して、dω=0になれば、閉形式という。微分形式ωが閉形式で、df=ωとなる1価関数fが存在する場合微分形式ωを完全微分形というのだ。


　これだけだと何の事やらわからん。
　だが、調べていくと重要な意味を持つ事を知る。
　連結と単連結と組み合わせると

　物理の法則が鮮やかに見える

　のだ。
　ガウスの法則やアンペールの法則が鮮やかな形で説明できるというのだ。


　まずは単連結と連結を見てみる。

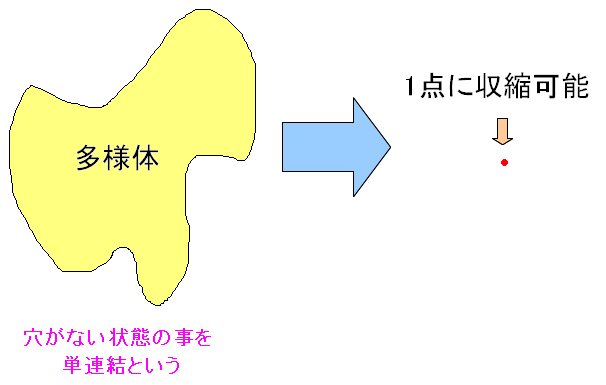
単連結

多様体(空間)を圧縮して1点になる場合を単連結という。要するに空間中に穴(特異点)がない状態だ。


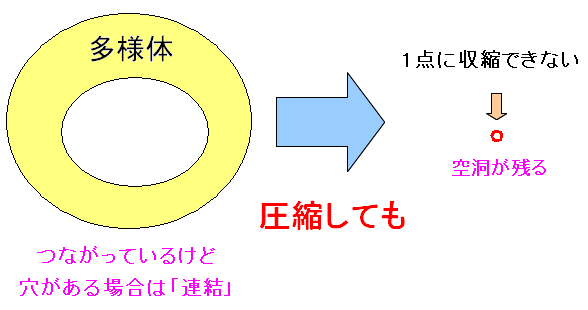
　そして連結は以下の事をいう。

連結

多様体(空間)を圧縮しても1点にならない場合を連結という。穴(特異点)があると、どうしても、この部分だけが残ってしまい 1点に圧縮できないのだ。


　単連結と完全微分形との間には、ポアンカレの補題が成り立つ。

ポアンカレの補題
単連結の空間では、どの領域をとっても連続で微分可能なのだ。そのため任意の微分形式ωが閉形式ならば、完全形式が成り立つのだ。ここでは証明しないし、証明できるだけの数学力はないのだ。


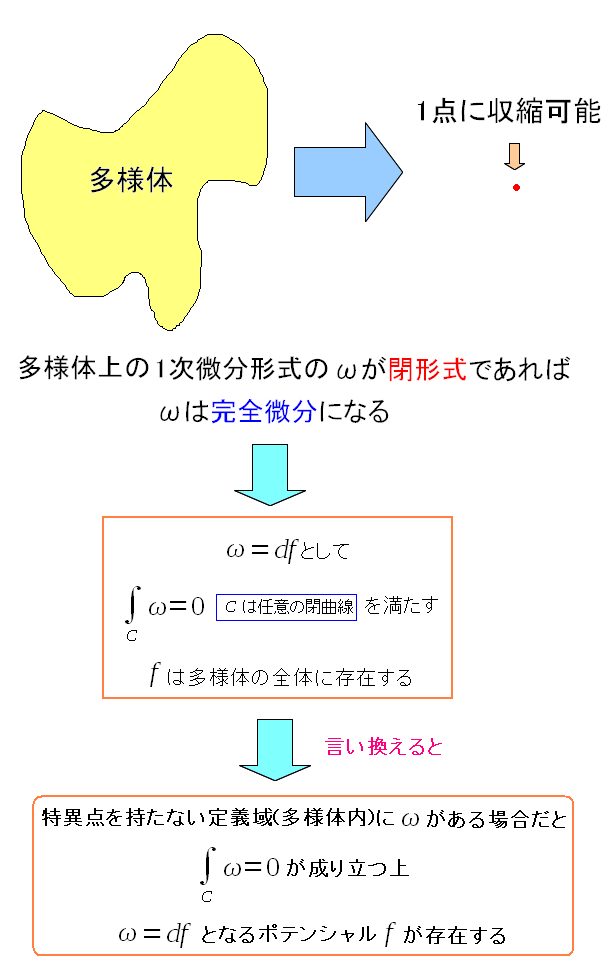
　単連結の空間、閉形式なら完全形式が成り立つ。
　そのため以下の事も言えるのだ。

単連結と完全微分形

単連結の空間では、1次微分形式のωを経路を1周させる経路積分をすると積分結果はゼロになるというのだ。


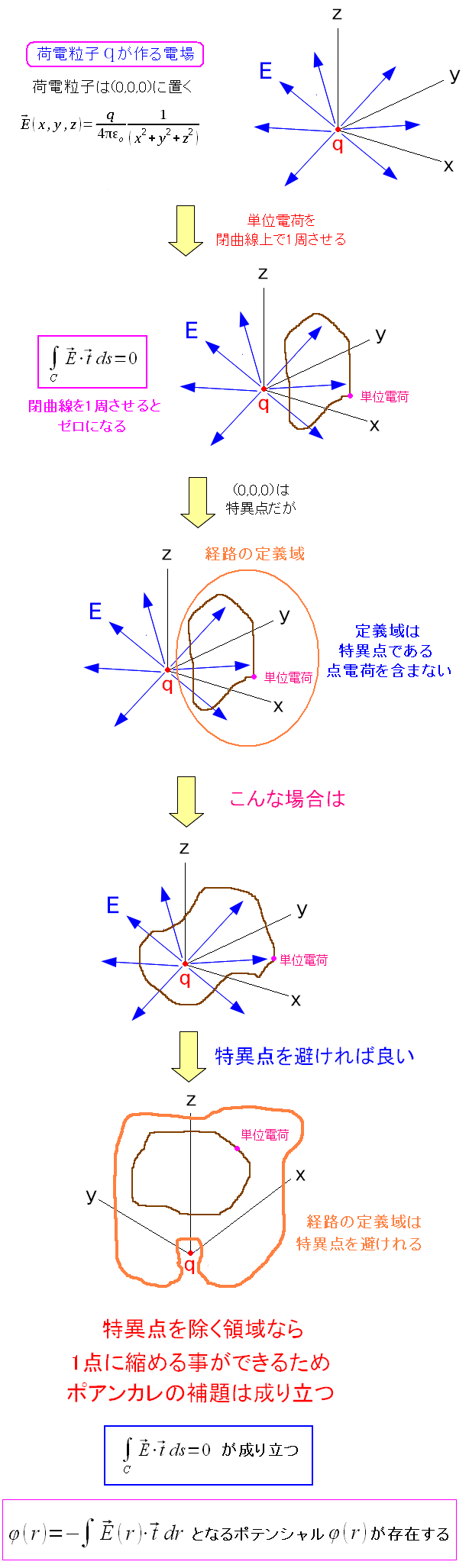
　すると、静電場の渦なしの法則(積分形)が説明できる。

静電場の渦なしの法則(積分形)が説明できる

電場Eが完全微分形の場合、電荷を横切らない限り経路を1周する経路積分がゼロになるのだ。そして完全微分形の場合、はポテンシャルが存在するので 1次微分形式である電場には、電位ポテンシャルの存在が示せるのだ。


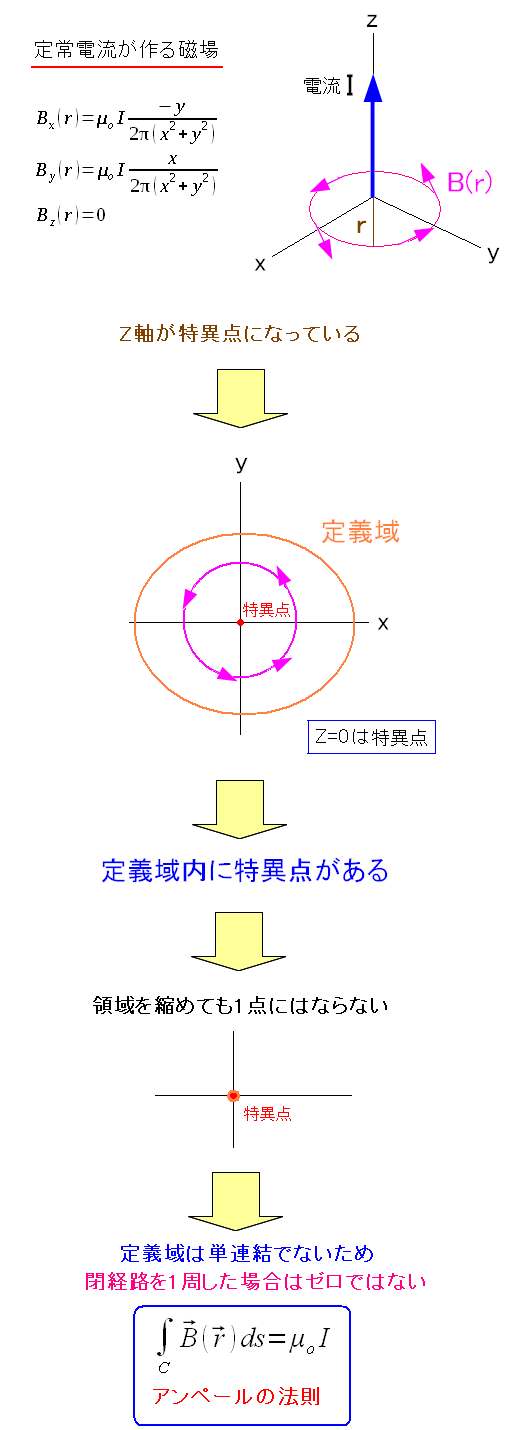
　そして特異点がある場合は、経路積分はゼロにならないのだ。
　アンペールの法則で見てみる

微分形式とアンペールの法則

Z軸が特異点になっている。
中心を1周する経路の場合、特異点を避ける事はできない。
そのため経路積分の結果はゼロにはならないのだ。

アンペールの法則の話で取り上げた際は
導線を流れる電流と、その磁場は比例関係にあると説明した。
物理現象では電流と磁場の対応関係なのだが、数学の観点で見ると
平面上にある特異点を1周した時の経路積分になるのだ。


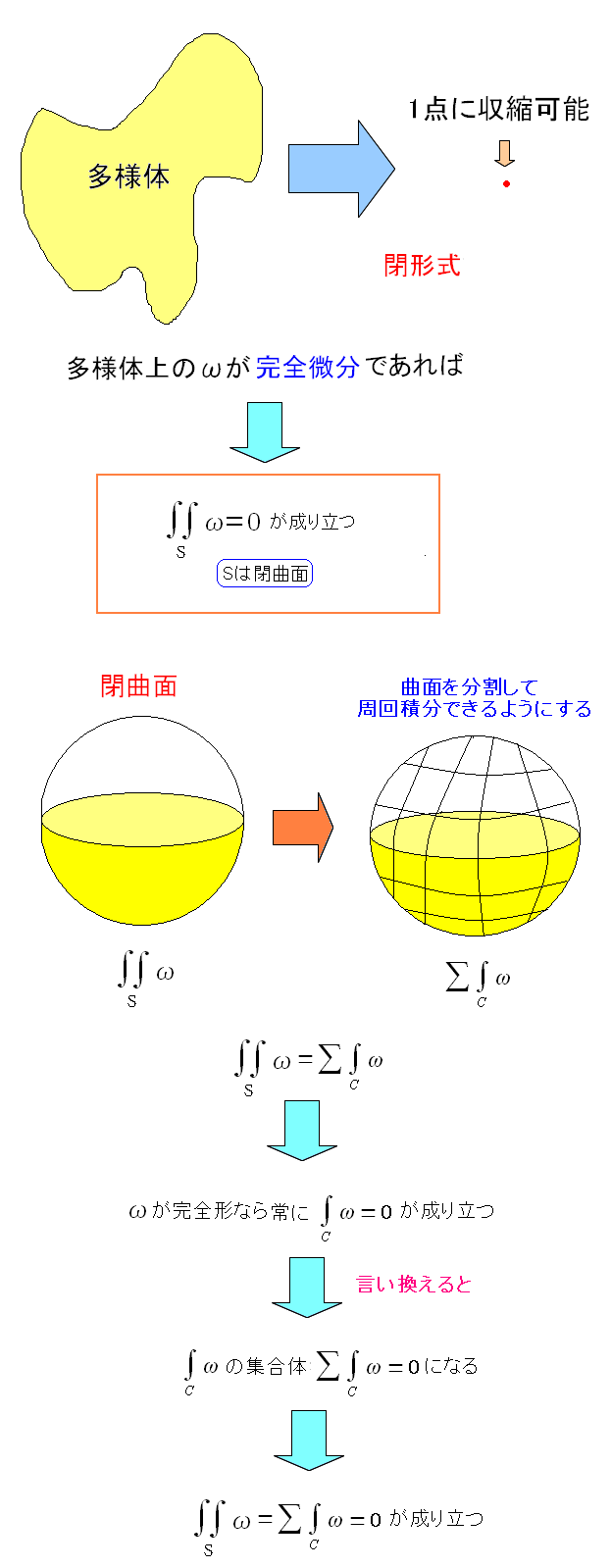
　単連結で、かつωが完全微分の場合、次の事が成り立つ。

単連結で、かつωが完全微分の場合

ωを覆う閉曲面の面積分がゼロになるのだ。考え方としては、ストークスの定理が成り立つ周回の領域はゼロなのでそれを張り合わせて、ωを覆う球体にしてしまっても、ゼロだというのだ。私には証明はできない。そんな頭はないのだ。


　なんと・・・

　ガウスの法則は、ストークスの定理の拡張版!!

　驚きとしか言いようがない。

　対称とする空間の周囲を、面で覆って面積分するのと
覆う面の周囲を周回積分した物の合計が同じになるというのだ。

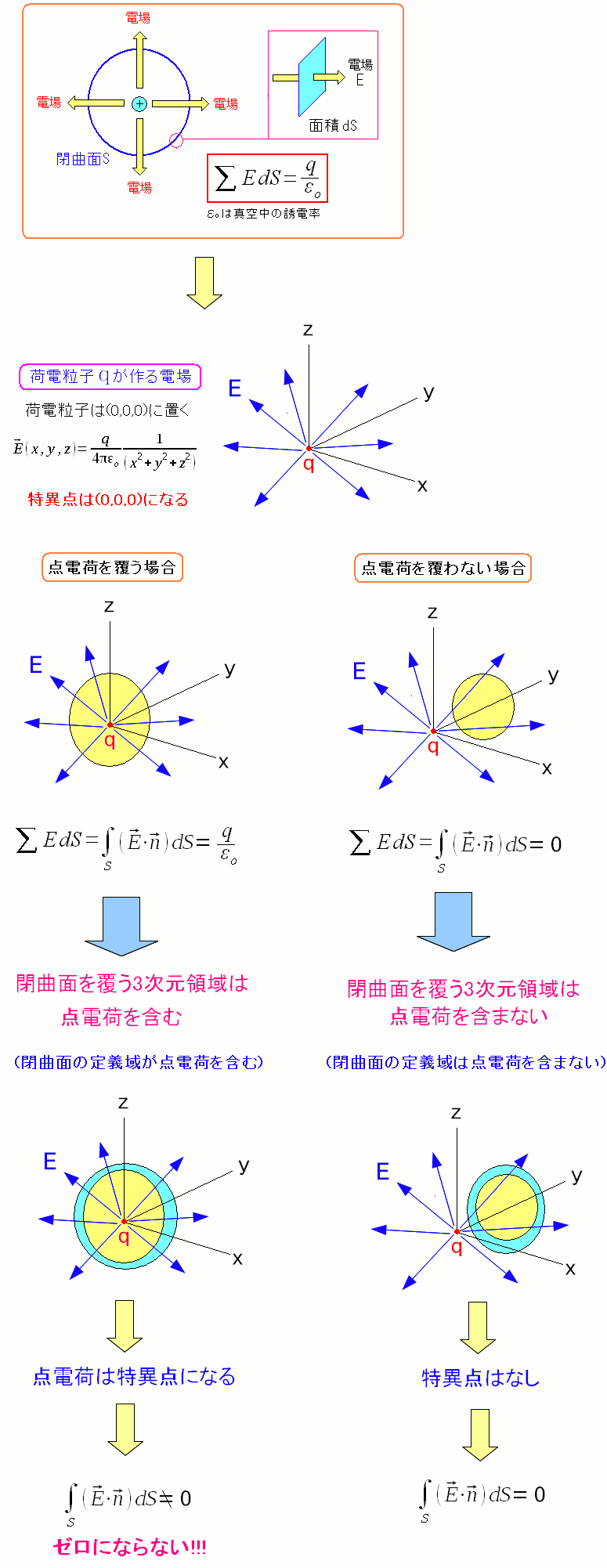
　ガウスの法則の積分形が数学的にすっきりするのだ。

ガウスの法則の積分形が数学的にすっきりする

点電荷を覆わない領域だと特異点が存在しない。電場の経路積分はゼロになる。そのため面積分はゼロになる。だが、閉曲面内に点電荷(特異点)がある場合、経路積分がゼロとは限らない。そのため面積分もゼロにはならないのだ。これが数学的なガウスの法則の積分形になるのだ。


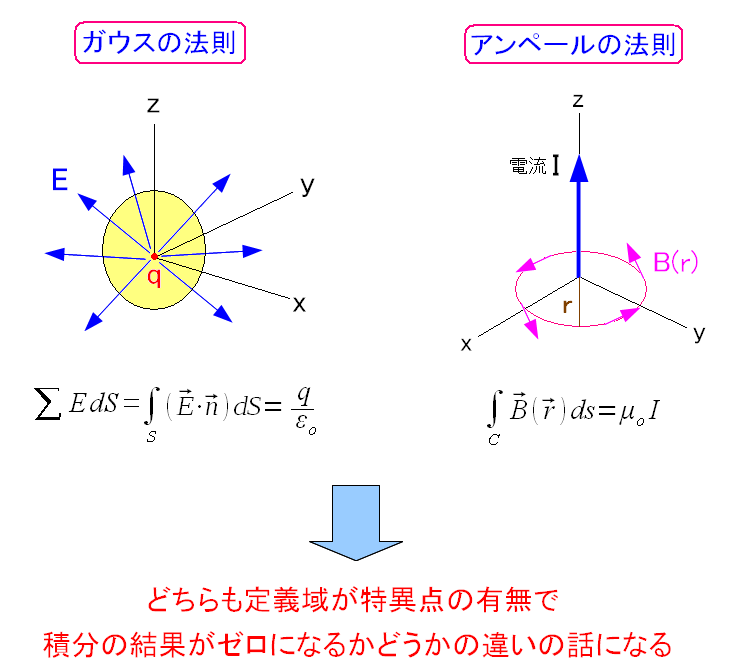
　ガウスの法則の積分形、アンペールの法則。
　定義域に特異点の有無によって、値が異なる事がわかった。

定義域に特異点の有無によって、値が異なる


微分形式とストークスの定理

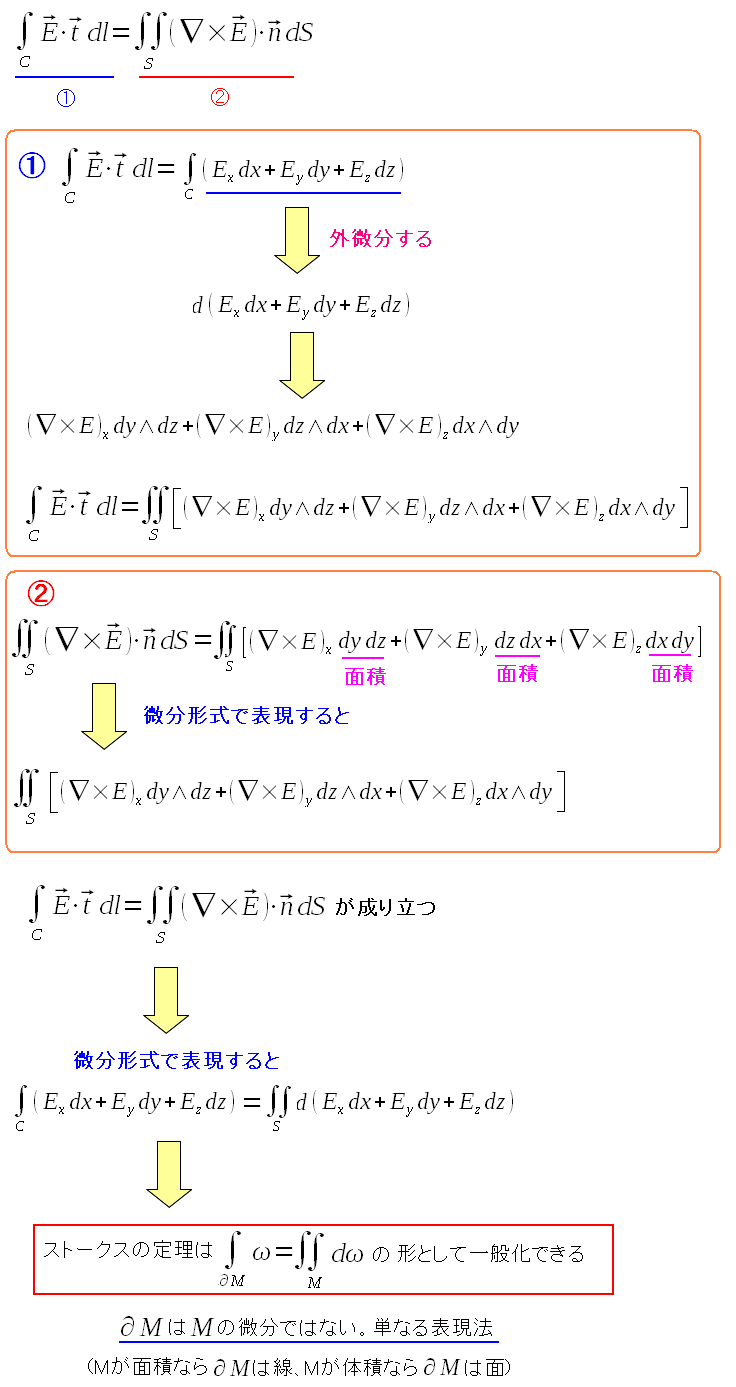
　微分形式の威力の凄さを感じる。
　そしてストークスの定理も微分形式だとすっきりするのだ。

ストークスの定理と微分形式

微分形式でストークスの定理が表現できる。座標系に依存しないという事だ。


　そしてガウスの定理も微分形式を使えば、すっきりする。

ガウスの定理と微分形式

微分形式でガウスの定理が表現できる。座標系に依存しないという事だ。


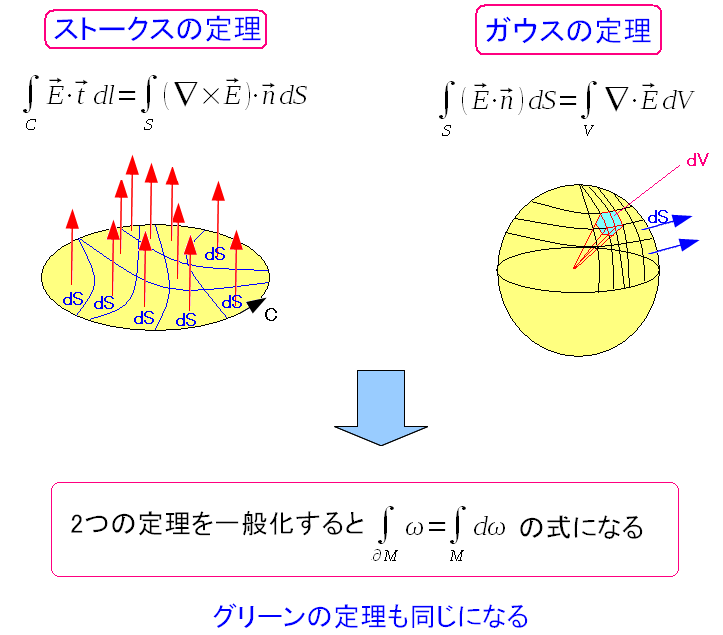
　ストークスの定理もガウスの定理も、一般化すると以下の形式になる。

ストークスの定理、ガウスの定理を一般化する

同じ形式の式になってしまう。この形式の式は、2次元のグリーンの定理にも当てはまるのだ。


　ここまで来ると・・・

　狐につつまれた感じ

　なのだ。

　ポアソンの方程式を微分形式を使ってみてみる。

ポアソンの方程式


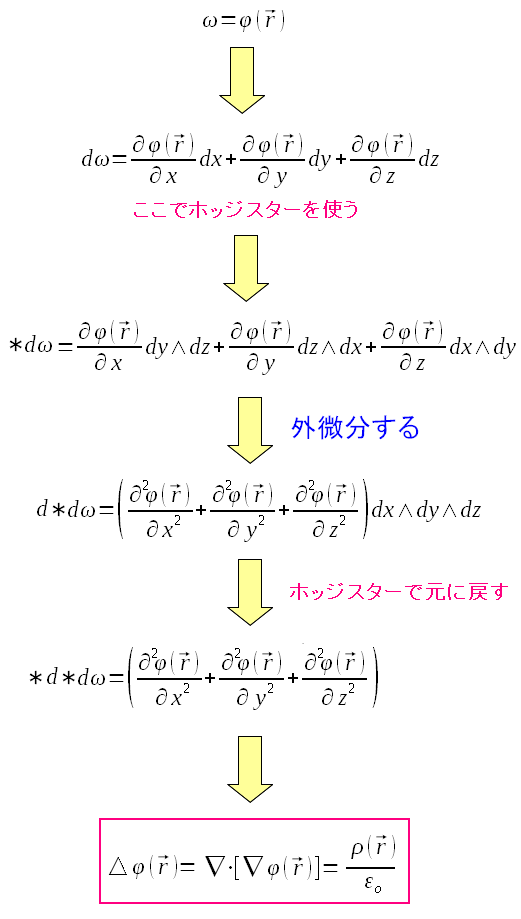
　早速、電位ポテンシャルを微分していく。

電位ポテンシャルを外微分する

外微分して1次微分形式を求めると、すぐにホッジスターを使って 2次微分形式に変換する。 2次微分形式で外微分した後、ホッジスターで、スカラーにするのだ。手がこんでいるが、微分形式を使ってポアソンの方程式が導けたのだ。


　ふと思った。

　ホッジスターは何のために使うねん?

　何か意味があるはず。
　だが、調べても

　わからへん・・・

　なのだ。
　そもそも、すぐに理解していたら、今頃、数学に強い人間になっているはず。
　わからないまま、前に進む。


　次にガウスの法則の微分形(湧き出し)を微分形式を使って求めてみる。

ガウスの法則の微分形(湧き出し)を微分形式を使って求めてみる

ここでもホッジスターを使っている。でも、きちんとガウスの法則の微分形が求まるのだ。


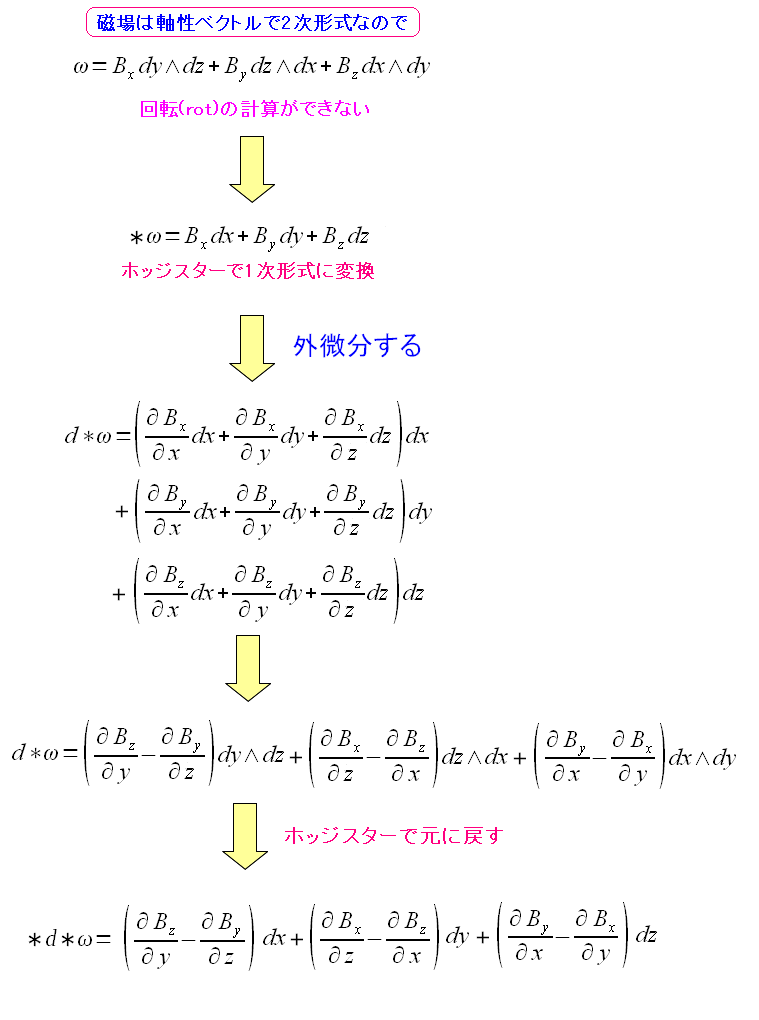
　次に静磁場の渦なしの法則を求めてみる。

静磁場の渦なしの法則を求めてみる

ここでもホッジスターを使っている。でも、きちんと静磁場の渦なしの法則が求まるのだ。



ヘルムホルツの定理

　ところで任意のベクトル場は、極性ベクトルと軸性ベクトルでできている。
　微分形式でいうと、1次微分形式と2次微分形式の合成なのだ。

ヘルムホルツの定理

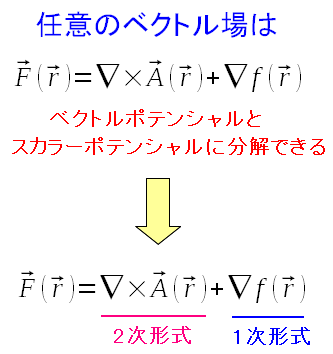任意のベクトル場は、1次微分形式と2次微分形式の合成なのだ。


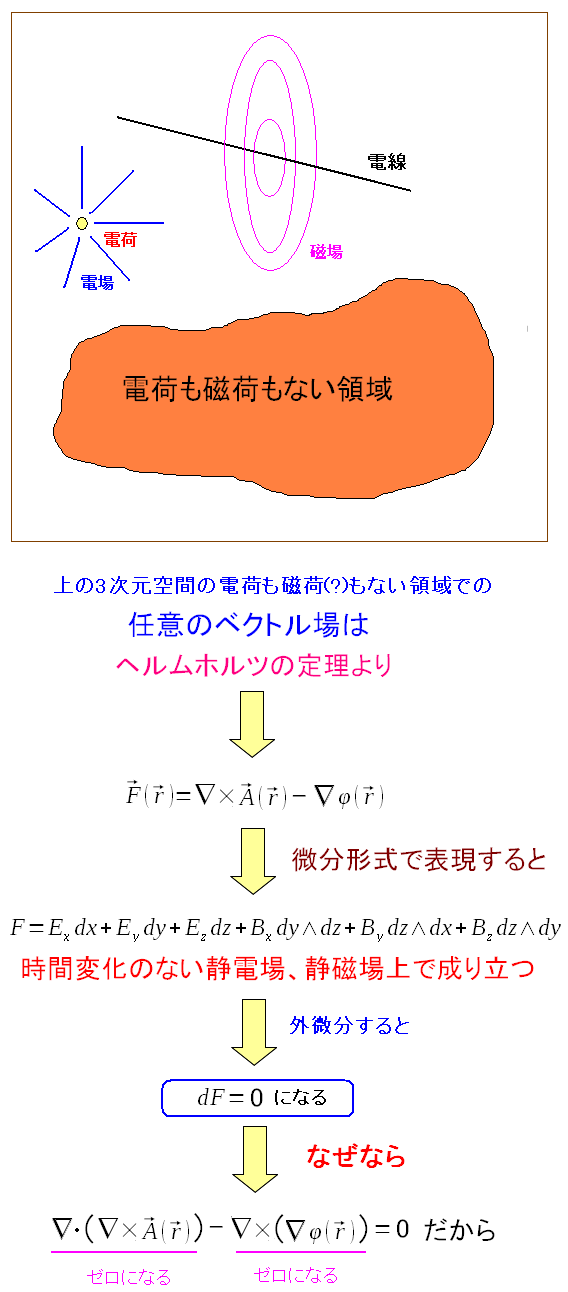
　そこで電荷も磁場の発生源もない空間のベクトル場を考えてみる。

電荷も磁場の発生源もない空間のベクトル場を考えてみる

1次微分形式(電場)と2次微分形式(磁場)の合成になっている。電荷も磁場の発生源もないので、外微分するとゼロになるのだ。



ミンコフスキー空間と微分形式

　ここまでは時間依存しない静電場、静磁場で考えてきた。

　ファラデーの誘導起電力のように電場、磁場が時間変化する場合を見てみる。

時間変化する場合は、どう考えるのか

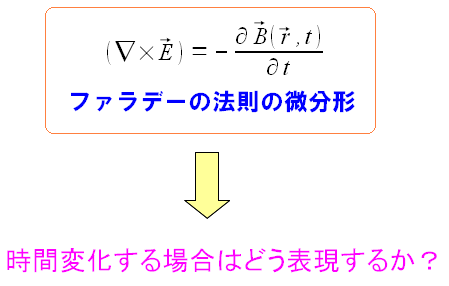時間変化する場合は、3次元の微分形式が使えないのだ。


　だが、時間の変化を考慮した微分形式はあるのだ。

　ミンコフスキー空間での微分形式

　なのだ。

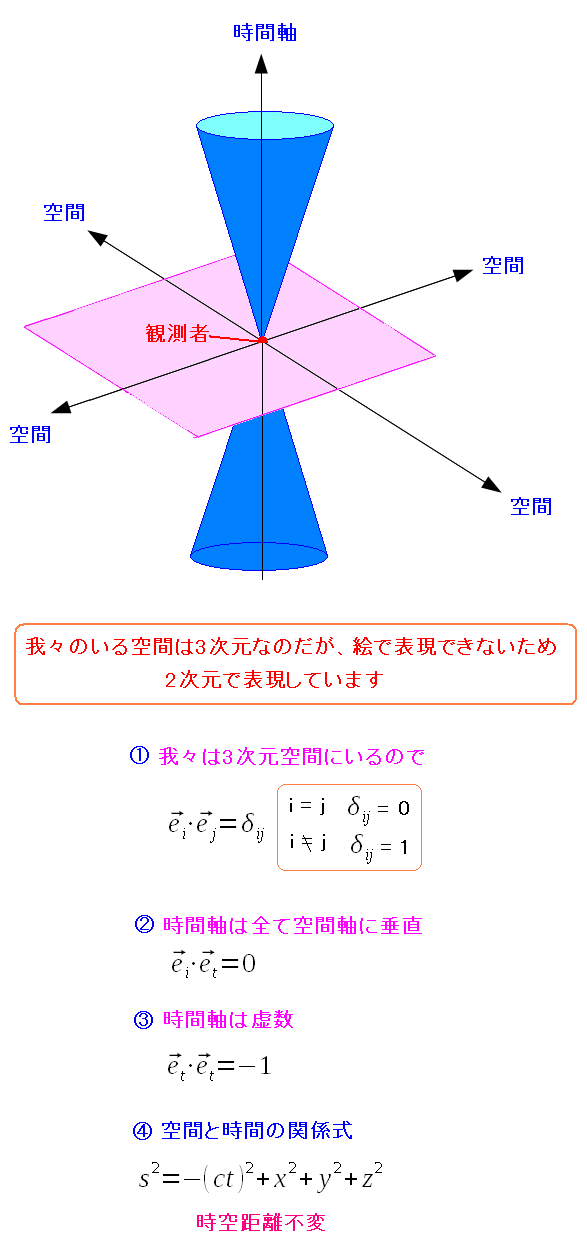
ミンコフスキー空間

ミンコフスキー空間とは3次元に、時間軸を加えた4次元空間なのだ。紙の上では4次元は表現できないため、平面を3次元にみたてて縦軸を時間軸の次元とした空間で考えるのだ。


　自分でも何をやっているのか、わからんようになっている。
　それにミンコフスキー空間とは

　相対性理論の話

　になってくるのだ。

ミンコフスキーとは
ドイツの数学者で、アインシュタインの数学の先生でもある。彼は特殊相対性理論を支えるために、ミンコフスキー空間を提唱したわけではない。だが、結果的に、特殊相対性理論に、ミンスフスキー空間を活用すると綺麗な形に収まる事がわかったというのだ。物理学者と数学者が全く違う目的で研究しているのになぜかつながってしまうのが、面白い所なのだ。

ミンコフスキーとは

ドイツの数学者で、アインシュタインの数学の先生でもある。
彼は特殊相対性理論を支えるために、ミンコフスキー空間を提唱したわけではない。
だが、結果的に、特殊相対性理論に、ミンスフスキー空間を活用すると
綺麗な形に収まる事がわかったというのだ。

物理学者と数学者が全く違う目的で研究しているのに
なぜかつながってしまうのが、面白い所なのだ。


　完全に資料や本の丸写し

　なのだ。
　そしてミンコフスキーの4次元空間を使った微分形式で
ファラデーの誘導起電力を表現してみるのだ。

ファラデーの誘導起電力を微分形式で表現

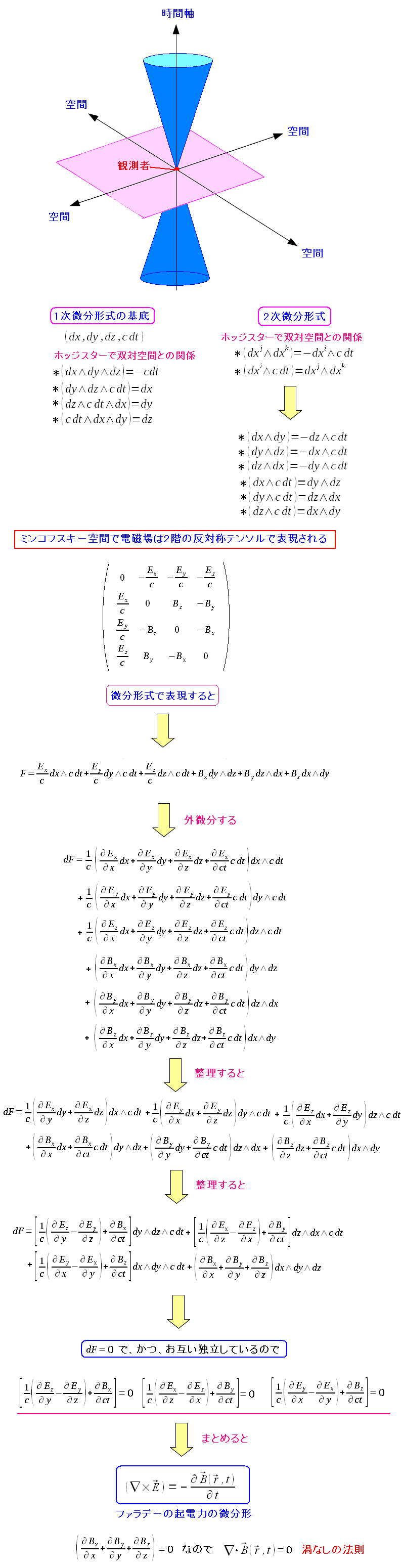ミンコフスキー空間だと、基底が上のようになる。ベクトル場(電場と磁場)を用意する。ヘルムホルツの定理なのだ。そして外微分すると、ファラデーの誘導起電力の式が求まったのだ。


　自分でも何をやっているのか、わからんようになってきた。

　ただ、次の事は言える。

　多様体や微分形式を使う事で

　物理の世界を綺麗に表現できる

　という事と

　物理の裏に潜んだ数学の世界が垣間見える

　という事だ。


　ファラデーの誘導起電力の法則で、微分形を取り上げた際、色々な資料を読んでも
説明に対して釈然としなかった部分が、少し見えたように思えたのだ。

∇(ナブラ)の正体とは

　微分形式を見てきた。∇(ナブラ)の正体がハッキリと見えてきた。
　微分演算子と、接ベクトルの顔を持った物になる。

∇(ナブラ)の正体
grad	スカラー関数(0次微分形式)の勾配を求めるための微分演算子スカラー関数をfとすると、「∇f」という形で表記するのだ。
rot	ベクトル(1次微分形式)を微分するための表記「∇×E」という形で表記する。∇をベクトルとすれば外積(クロス積)で表記すると、計算式通りになるので、すっきりした形になるのだ。
div	ベクトル(2次微分形式)の微分をするための表記「∇・E」という形で表記する。内積で表記する事で、計算式通りになりすっきりした形になる。


　∇(ナブラ)とは、スカラーやベクトルを

　微分するための微分作用素であり、微分演算子

　だったのだ。


　計算上、かつ便宜上の理由で、ベクトルの微分の形を
∇(ナブラ)との外積表記や、内積表記になったりしている。
　そして、rotやdivと表記しているので混乱しやすくなるのだ。


電磁気学入門の目次

電磁気学入門:目次
スカラーとベクトル	簡単なスカラーとベクトルの話です。ベクトルは方向と大きさを持つ量。方向という量持っているだけに注意が必要です。
静電気の発見からクーロンの法則	今でこそ当たり前の静電気や導体、絶縁体、電荷などどういう経緯で発見し、クーロンの法則まで至ったのかの話です。
クーロン力、電場、近接作用	4つの力のうち、クーロン力の位置づけ電荷が作り出す作用の電場。近接作用の話です。
微分、全微分、方向微分	簡単な微分、全微分、方向微分の話です。ここをしっかり押さえないと、電磁気の数式の意味がわからなくなります。
ベクトル解析	電磁気に必要なベクトル解析の話です。勾配(grad)、2次元のグリーン定理ストークスの定理の話です。
電位ポテンシャル	電位ポテンシャルです。勾配と電場の関係を使って説明しています。
電気双極子	電気双極子の話です。物質中で起こる分極を理解するのに必要です。
ガウスの法則	ガウスの法則の積分形、微分形の話です。
ポアソンの方程式、ラプラス方程式	ポアソンの方程式、ラプラス方程式の話です。単に電荷分布から電位を求めるだけの話にとどまらない奥が深い分野です。ポテンシャル論、デルタ関数グリーン関数、固有値問題について触れています。
静電場と渦なしの法則	静電場で、電荷を1周させた時の仕事はゼロ微分形と微分形の渦なしの法則の話です。
ビオサバールの法則	電気と磁場の関係の発見の話からビオ・サバールの法則が導かれるまでの話です。
磁気双極子	磁気双極子の話で、回転電流になります。物質中の磁場の話にも関連します。
アンペールの法則	アンペールの法則の話です。積分形・微分形だけでなく、閉回路に流れる電流が作る磁気双極子の話なども書いています。
ローレンツ力	磁場中を移動する電荷にかかる力(ローレンツ力)の話です。ローレンツ力は相対性理論が絡んでいる事も紹介しています。
ファラデーの誘導起電力の法則	ファラデーの誘導起電力の話です。
うず電流を使った簡単な物理実験	電力計に使われるアラゴの円盤。そしてIH調理器で熱するために発生させる、うず電流はレンツの法則から電流が発生する原理を応用した物だ。アラゴの円盤の実験と、IH調理器を使った実験です。気分転換で読んでください。
ベクトルポテンシャル	わかりにくいベクトルポテンシャルの話です。電位は電荷が作る電気のポテンシャルだがベクトルポテンシャルは電流が作る磁場のポテンシャルの話です。
オームの法則の微分形	微小領域でのオームの法則の話です。
マックスウェルの方程式	4つのマックスウェルの方程式を書いています。電場と磁場の変化を図にする事で rotの回転の意味も理解できます。
ゲージ変換	ゲージ(gauge)は物差しの意味です。マックスウェルの方程式をE（電場）とB(磁場)の関係式から φ(電位ポテンシャル)とA(ベクトルポテンシャル)の関係式に書き換える際、ゲージ変換が使われます。ゲージ変換の役目を書きました。
電磁波	マックスウェルの方程式から電波が伝わる様子を視覚的に見てみる話です。
回転のrotはベクトルの微分	ベクトル解析や渦なしの法則で出てくるrotはベクトルの微分という話です。
電磁気学の単位系	電磁気学の単位系の話です。物理量の単位系の指数を見る次元解析電磁気学の歴史と単位系の変遷について触れました。
電気泥棒:電気と法律の話	電気は物体なのか、無形物なのか。明治時代に、電気を無断で使った場合、物か、そうでないかで窃盗罪になるかどうかが裁判で問われました。ちょっとした科学と法律の話です。気分転換で読んでください。
数ベクトルと基底ベクトル	ベクトルの話です。矢印だけがベクトルでない事。数ベクトルと基底ベクトルの違いの話です。多様体、反変・共変ベクトルを理解するのに必要です
多様体	空間を一般化した話です。 ▽(ナブラ)の正体に迫まります
外積代数	外積、テンソルについて書いています。極性ベクトル、軸性ベクトル外積は行列で、ベクトルは見せかけの姿だった話です。
ベクトルの双対関係	反変ベクトル、共変ベクトル、双対関係ベクトル解析、外積代数の話外積、テンソルについて書いています。
ローレンツ力と相対性理論	磁場は電場の相対論的効果だった話です。ローレンツ力を使って、導線が作る磁場を使って説明です。
微分形式	多様体の話の続きです。座標に依存しない形での関数やベクトルの微分の話です。ガウスの法則、アンペールの法則、マックスウェルの方程式が鮮やかな形で表現できます。 ∇(ナブラ)の正体もわかります。
物理と対称性	マックスウェルの方程式をよく見ると対称性があります。物理の方程式と対称性を数学的な観点でみると意外なつながりがあるという話です。
マックスウェルの応力	電気力線を弾性体(ゴム)とみなして、力の伝わり方などを説明した考え方です。
電場エネルギー	電場が持つエネルギーの式を導いた話です。
磁場エネルギー	磁場が持つエネルギーの式です。手抜きの説明と、直流RL回路を使った説明を書きました。
ポインティングベクトル	電磁エネルギーの流れ「ポインティングベクトル」の話です。電磁波でもエネルギー保存則が成り立つ話からポインティングベクトルを導いています。
電気エネルギーは導線の外を伝わる	導線の外を電気エネルギーが流れる話です。私が誤解した事、その誤解を解いていく過程を紹介しながら「目からウロコ」にたどり着いた話です。
物質中の電場	物質中の電場の話です。分極の話をしながら、物質中の電場の話をします
物質中の磁場	磁性の話をしながら、物質中の磁場の話をします
物質中のマックスウェルの方程式	物質中でもマックスウェルの方程式が成り立つ話です。
導体に侵入する電磁波	導体に侵入する電磁波が減衰していく話です。表皮効果と同じ「表皮の厚さ」が出てきます
表皮効果	目的の表皮効果の話です。マックスウェルの方程式を解きながら交流電流の周波数を上げると、表面にしか電流が流れなくなる話です。

電磁気学の目次:「電磁気学入門」に戻る

前章:「無線LANの基礎無線LAN入門と導入事例」を読む
システム奮闘記の目次:システム奮闘記に戻る