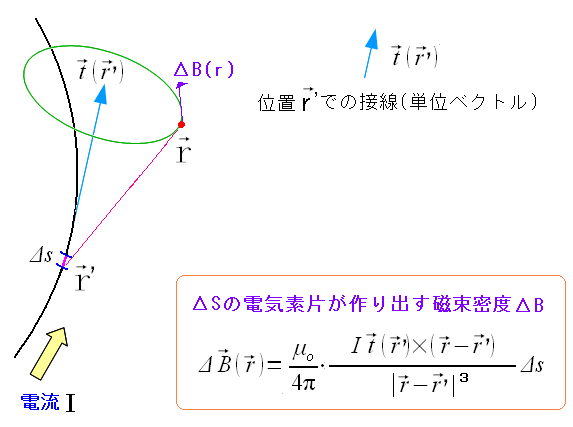
1820年、ラプラスが、上に近い式を予言し、ビオサバールが実験的に証明したのだ。
システム奮闘記:その105
(2016年5月22日に掲載)
ビオサバールの法則の式
電場の話が一段落した所で、次は磁場の話に入っていく。 電流と、それが作り出す磁場との関係式がある。 それが・・・ ビオサバールの法則 なのだ。
| ビオサバールの法則 |
|---|
 |
|
電流と、電流が作る磁気の関係式がビオサバールの法則だ。 1820年、ラプラスが、上に近い式を予言し、ビオサバールが実験的に証明したのだ。 |
磁場と磁束密度
ところで磁場と電流の関係式がビオサバールの法則なのだが 上の式では電流と磁束密度の式になっている。 磁場と磁束密度の違いは何やねん!! なのだ。 まず磁場が何かを見てみる。
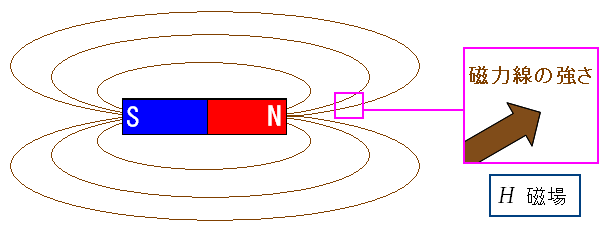
| 磁場とは磁力の強さ |
|---|
 |
|
磁場とは磁力の強さを表わす。 Hの記号を使うのだ。 |
次に磁束とは何かを見てみる。
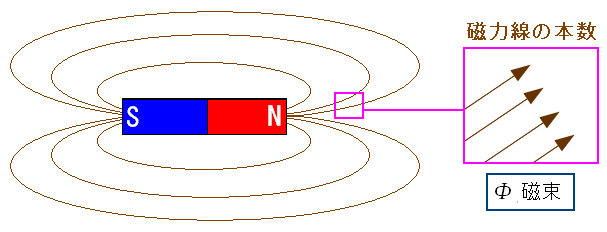
| 磁束とは磁力線の本数 |
|---|
 |
|
磁束とは磁力線の本数だ Φ(ファイ)の記号を使うのだ。 |
次の磁束密度は何かを見てみる。
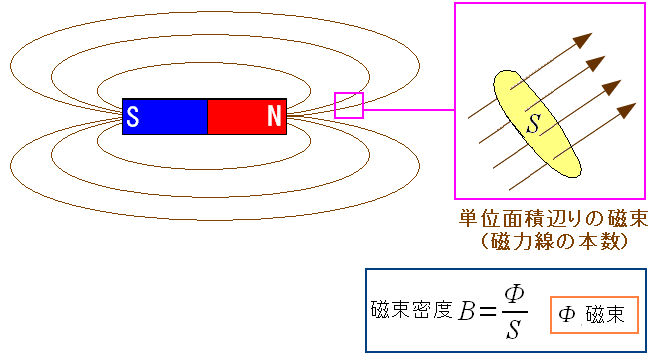
| 磁束密度とは単位面積辺りの磁力線の本数 |
|---|
 |
|
磁束密度とは単位面積辺りの磁力線の本数だ Bという記号を使うのだ。 |
磁場が磁力の強さ。磁束密度が単位面積辺りの磁力線の本数だとわかった。 この2つの関係を結ぶ式がある。
| 磁場と磁束密度の関係式 |
|---|
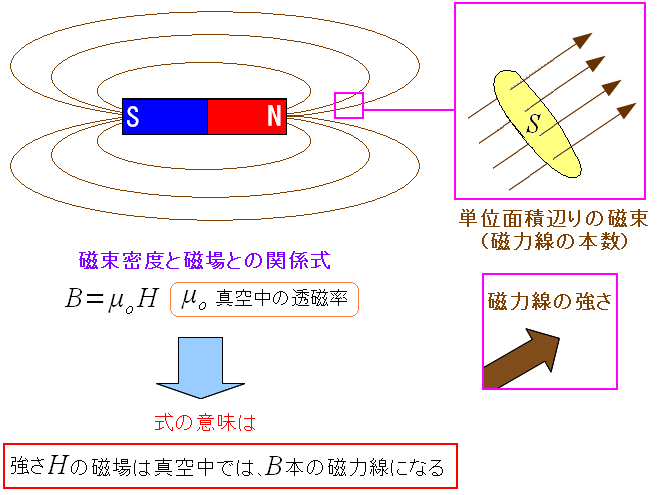 |
|
磁場(磁力の強さ)と、磁束密度(単位面積辺りの磁力線の本数)の関係式だ。 透磁率は物質によって異なる。 磁場に、透磁率の係数をかけると、磁束密度が求まる。 |
磁場と磁束密度の関係式。 この式は以下のような場合に使える。
| 磁場と磁束密度の関係式の使い方 |
|---|
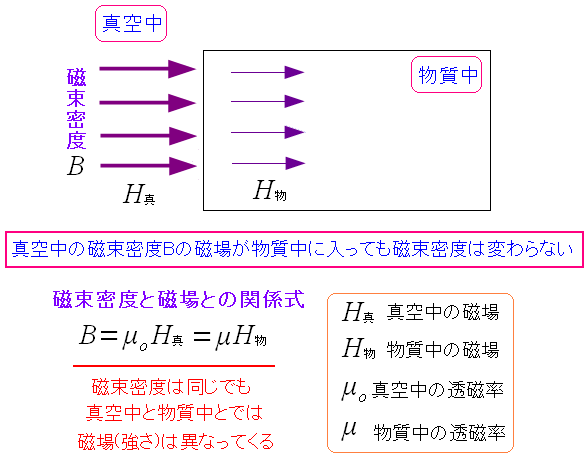 |
|
真空中の磁場が、物質内に入っても磁束密度(単位面積辺りの磁場の本数)は変わらない。 透磁率と磁束密度がわかれば、真空中や物質中の磁場の強さがわかるのだ。 |
同じ磁束密度にしても 磁束密度が通る物質が異なれば 磁場の強さは異なる これを頭に入れておくと、あとで出てくる物質中の磁場を考える上で便利になるのだ。
磁石の歴史と電磁気学の発展
このまま話を進めてアンペールの法則に行こうとした。 だが、幸か不幸か、次のサイトを見つけてしまった。 ビオ・サバールの法則(1820年)を見つけた方法 よく考えれば 何でこんな式が導けたのか 考えた事、あらへんかった!! 大抵の電磁気の教科書は、ビオサバールの法則を紹介するぐらいで なぜ、この式が導けて、実験的に証明できたのかが書かれていない。 そこで調べていくことにした。 磁石の歴史を調べていくと以下のサイトが見つかる。 永久磁石の歴史と磁気科学の発展年表(ネオマグ株式会社) 大いなる磁石、地球(京都大学大学院理学研究科附属地磁気世界資料解析センター) 磁石の歴史〜永久磁石の発見と未来〜(株式会社マグファイン) ギリシャ人が磁鉄鉱を発見し、鉄にひっつく事を発見したのだ。 ところで磁石の事を英語でマグネット(magnet)という。その言葉は・・・ ギリシャの「マグネシア」地方 が由来なのだ。 そんな事、今まで知らなかった。 そして古代・中国では羅針盤(方位磁石)を発明されたのだ。 これは誰でも知っている話なので、軽く流す。 日本でも磁鉄鉱は発見され 続日本紀に記述されている というのだ。 そんな事、知らなかった。 『続日本紀』国史大系版 巻第六(日本文学電子図書館)
| 「『続日本紀』国史大系版 巻第六」の一部を引用 |
|---|
|
《和銅六年(七一三)五月癸酉(十一)》○癸酉。相摸。常陸。上野。武蔵。下野。五国輸調。 元来是布也。自今以後。[糸+施の旁]・布並進。又令大倭参河並献雲母。伊勢水銀。 相摸石硫黄。白樊石。黄樊石。近江慈石。美濃青樊石。飛騨。若狭並樊石。 信濃石硫黄。上野金青。陸奥白石英。雲母。石硫黄。出雲黄樊石。讃岐白樊石。 |
|
赤い文字に注目。近江(滋賀県)で磁鉄鉱が献上された事が書かれている。 西暦713年の時点で、水銀や硫黄など化学物質が認知されているというのだ。 (「磁石の歴史〜永久磁石の発見と未来〜」の受け売り) 中国では磁石は慈州が磁鉄鉱の産地だった事から 磁石は「慈石」と言われていたのだ。 そして磁石の「磁」は「慈」に石片をつけた和製漢字なのだ。 でも「慈」から「心」が落ちているぞという突っ込みはナシでお願いします。 |
そして日本にも平安時代には羅針盤が入ってきているというのだ。
だが、当時は誰も、地球が磁石とは夢にも思わなかった。
それから時代が流れ1600年頃に、電気の歴史でも触れた
イギリスの医者で物理学者だったウィリアム・ギルバートが
地球は磁石だ!
を唱えたのだ。
それが「磁石論」(1600年出版)という本にもなっている。
| ギルバートが発見した事 | |
|---|---|
| その1 | 磁石は吸引力と反発力を持っている |
| その2 | 地球は巨大な磁石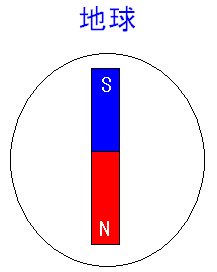
|
| その3 | 磁石を細かく切ってもNとSになる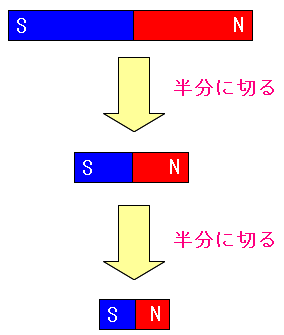 |
そしてギルバートは 磁化された鉄は熱すると、磁力を失う を発表した。 ただし、間違えた事も発表している。 電気と磁気は別物 と言ったのだ。 長らくそれが信じられてきたのだ。
| 当時の科学者は命がけ |
|---|
|
当時、科学者がカトリックの教えに反する意見を述べると 異端扱いされ、最悪、火あぶりになった。 1600年に宇宙の無限性を唱えたブルーノが火あぶりになっただけに ギルバートは怯えながら、磁気論を書いた事が想像できる。 当時はカトリックの教義に反しないように、上手に配慮しないければならず 科学者受難の時代だったのだ。 |
電気と磁気は別物という考えが200年の間、定着していたのだが エルステッドが1820年7月に以下の事を発見してしまう。
| 導線の下に方位磁石を置く実験 |
|---|
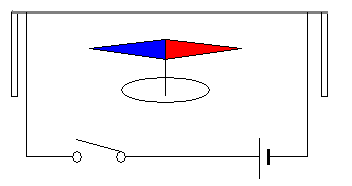 |
|
講義中に、実験器具をいじっていたエルステッド。 電線のスイッチを入れたり、切ったりしていた。 たまたま、近くに方位磁石が置いていた。 |
導線に電気が流れると、方位磁石が動いたのだ。
| 導線に電気が流れると、方位磁石が動いた |
|---|
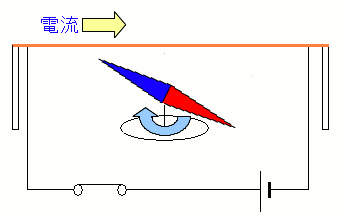 |
| 導線に電気が流れると、側にあった方位磁石が動いた。 |
そのため・・・
電流によって磁気が発生する
と発表したのだ。
その発表がすぐに広まって、電流と磁気の関係を確かめるべく
色々な実験が行なわれた。
ビオサバールの実験内容を見る。
そのために、実験方法を理解するための準備を行なう。
電流と発生する磁気の向きだが、磁石を使う。
| 電流と発生する磁気の向き |
|---|
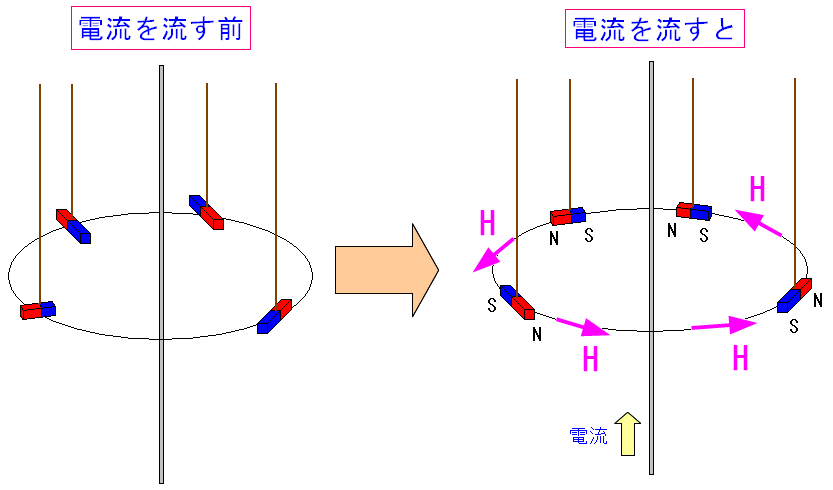 |
|
上図のように磁石を使うと、電流によって発生した磁気の様子がわかる。 電流の方向を上にして、反時計周りで磁気が発生しているのだ。 |
そして磁石を揺らしながら、導線に近づけたり、遠ざけたりして 揺れの周期を求める。
| 磁石の揺れの周期を求める |
|---|
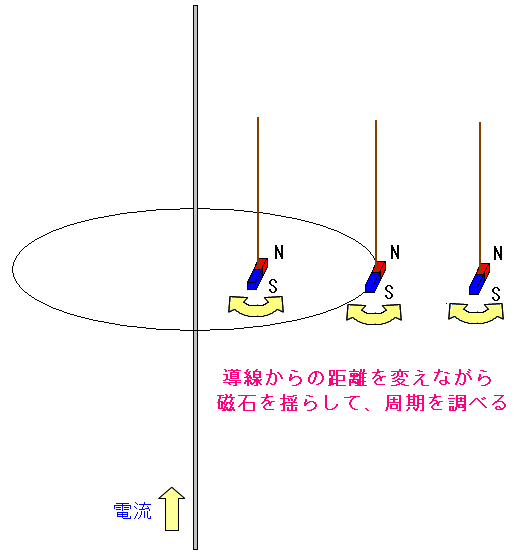 |
|
導線からの距離と揺れの周期を調べる事によって 磁気の強さがわかるというのだ。 |
揺れている磁石を真上から見た様子だ。
| 揺れている磁石を真上から見た様子 |
|---|
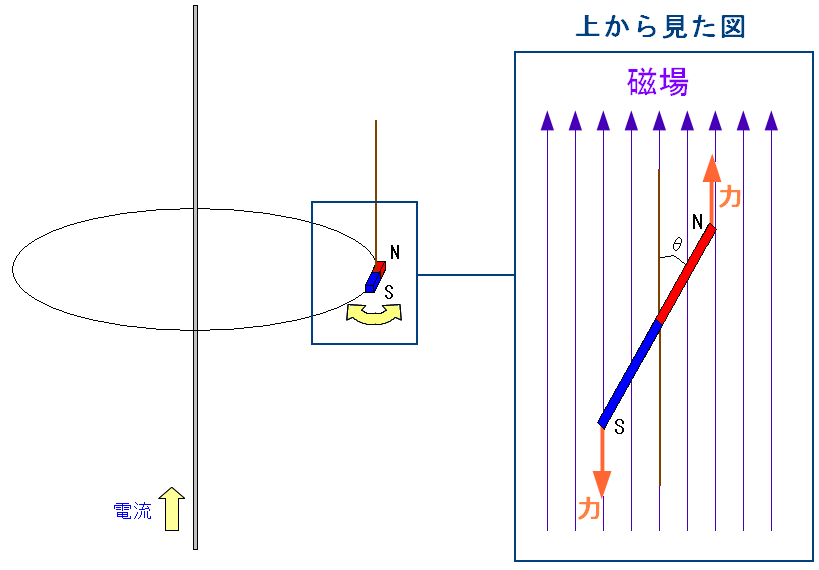 |
| 磁石の傾きを戻そうとする力が働いているのだ。 |
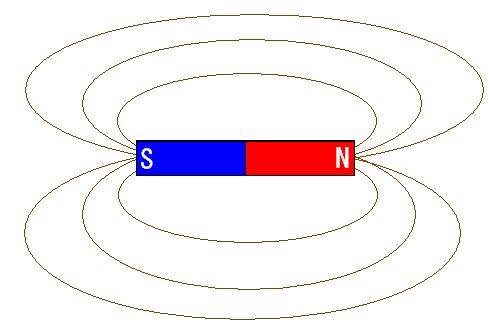
ところで磁石には磁力線というものがある。
| 磁石には磁力線というものがある |
|---|
 |
|
電気力線と同じ考え方だ。磁石にも磁力線があるのだ。 子供の頃、理科の実験で、紙の上に砂鉄をまいて 紙の下に磁石を置くと、磁力線が描き出される事をやった。 ファラデーは、別の方法で磁力線の概念を編み出したのだ。 1837年頃と言われている。 |
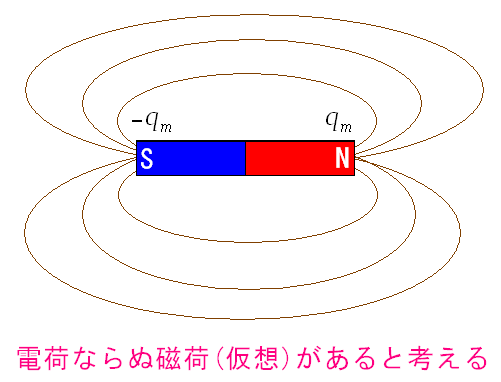
ところでビオサバールの法則は1820年なので、磁力線の概念はなかった。 だが、既にクーロンの法則が1785年に発見されている。 電気には電荷という物があり、それによって相互作用が働いた。 磁石にも、電気と同様、電荷と同じような物があると考えられた。 磁荷というものだ
| 磁荷の存在を仮定する |
|---|
 |
|
実際の所、磁荷は存在しないと言われる。 当時、何もわかっていないので、電気と同じだと類推して 磁荷の存在を仮定したのだ。 (注意) 磁荷が存在しないというのは、過去に話になるかもしれない。 日本で磁荷の存在を示唆する研究結果が出ているからだ。 磁気モノポールの量子ダイナミクスの発見(東京大学) N極・S極だけをもつ磁石・磁気モノポールの発見(首都大学東京:PDF) |
先人は磁荷を勝手に仮定したのだが、科学研究の場合
類似現象から類推した仮説を矛盾が出るまで使う
というのが行なわれている。
この考え方が、科学には必要だったりする。
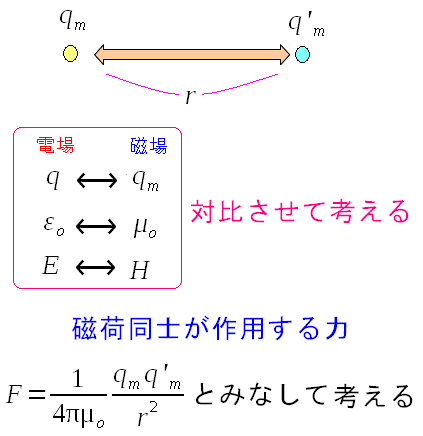
そしてクーロンの法則から類推した磁気版のクーロンの法則も考え出される。
| 磁気版のクーロンの法則 |
|---|
 |
|
当時、比例定数の中身の4πやμoはわかっていなかったのだが ここでは比例定数として書いたのだ。 わかりやすいよう、磁荷の添え字には「m」をつけている。 |
そして磁荷と磁場の関係式も、クーロンの法則から類推した物を使う。
| 磁荷と磁場の関係式(クーロンの法則から類推した物) |
|---|
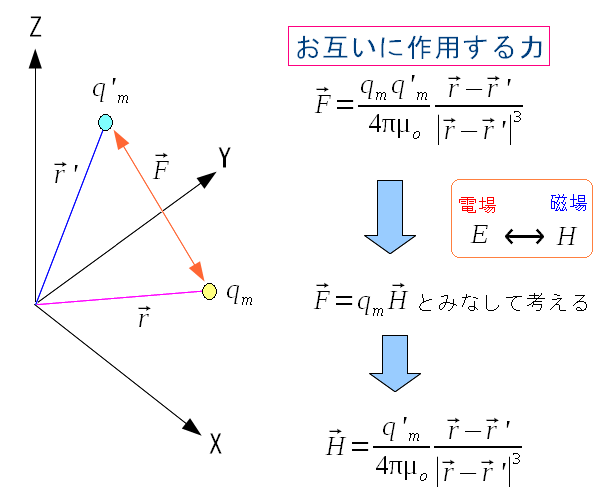 |
| 磁荷と磁場の関係式を類推した物だ。 |
電荷、電場、クーロンの法則から、磁荷と磁場を類推した。 そして、棒磁石を磁気双極子とみなすことができる。
| 棒磁石を磁気双極子とみなすことができる |
|---|
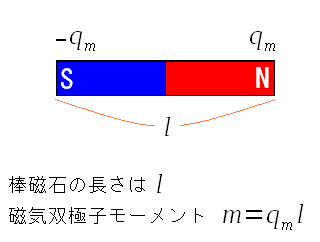 |
| 長さlで、磁荷qmの磁気双極子だ。 |
棒磁石(磁気双極子)に磁場を当てると、以下のようになる。
| 棒磁石(磁気双極子)に磁場を当てる |
|---|
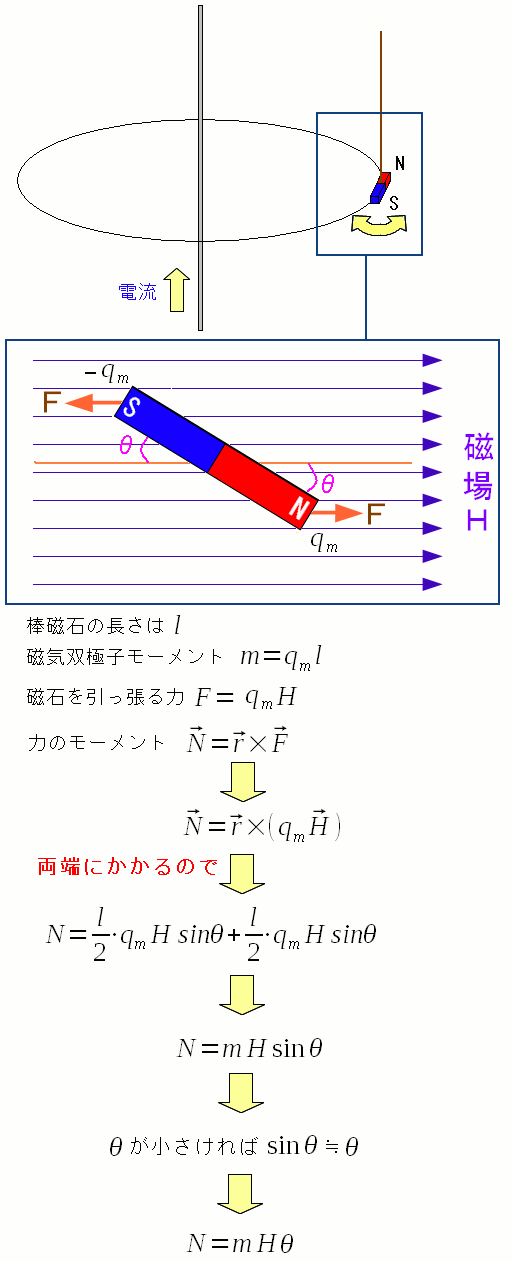 |
|
磁場に対して角度「θ」だけ斜めを向いているとする。 磁荷と磁場の関係式(クーロン力の類推)から、両側に力がかかり 棒磁石と磁場の向きが並行なるように働く。 |
力のモーメントが出た所で、角度「θ」だけ斜めにして磁場を流し 揺れの周期を計る事で、周期と磁場の力の関係式を求めてみる。
| 揺れの周期と磁場の力との関係式を求めてみる |
|---|
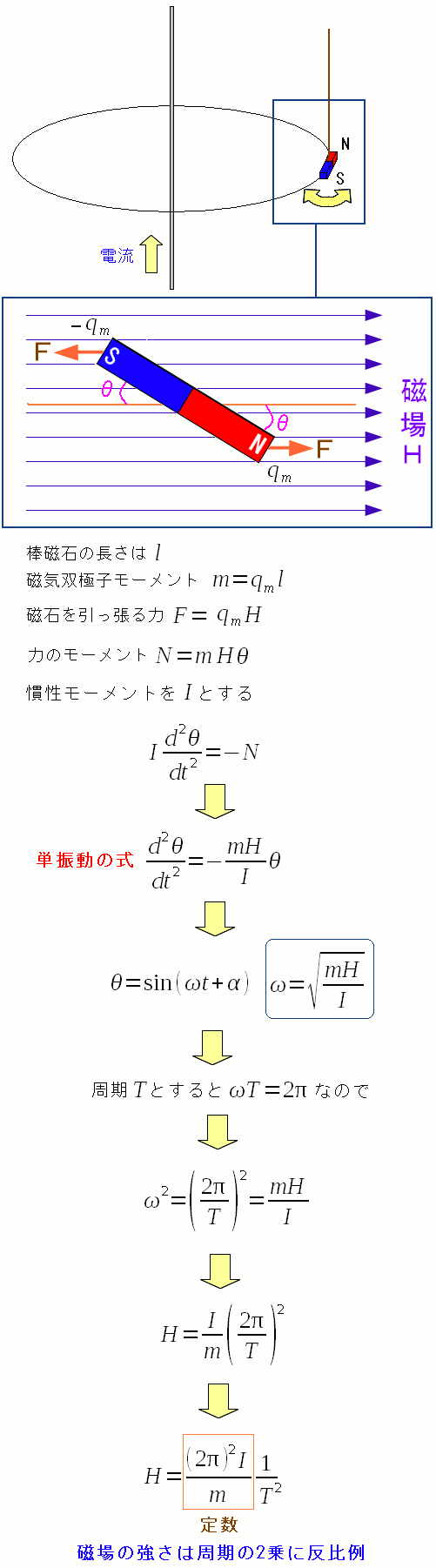 |
| 磁場の強さと、揺れの周期が、周期の2乗の反比例の関係が求まった。 |
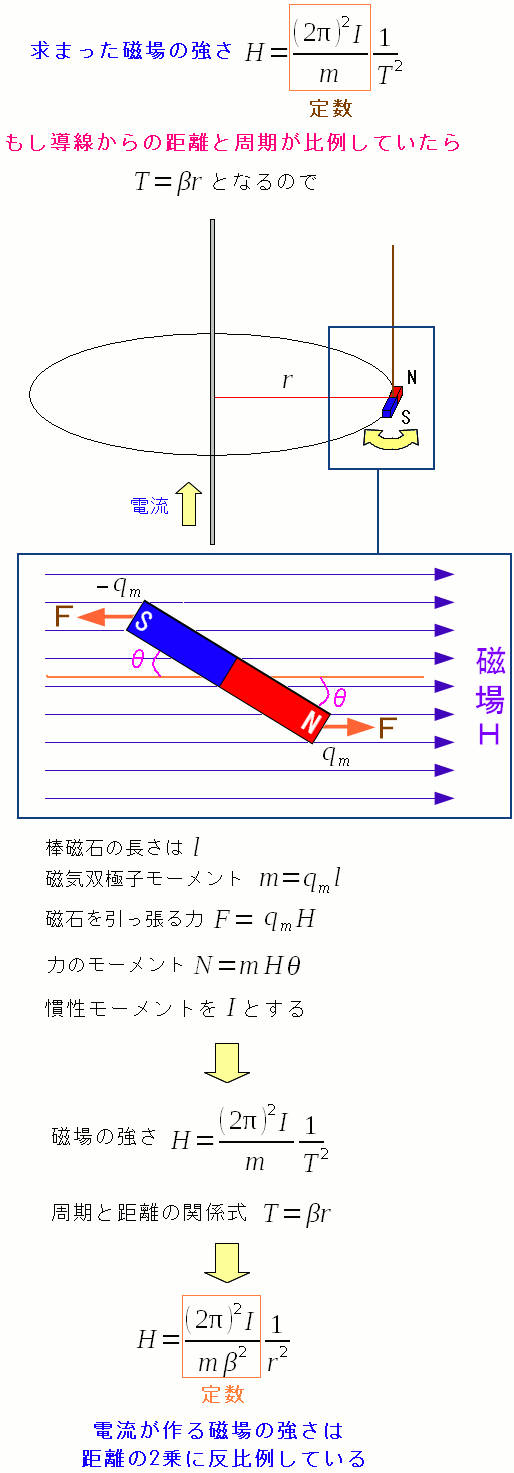
次に、導線からの距離と磁場との関係式を求めてみる。
| 導線からの距離と磁場との関係式 |
|---|
 |
|
周期と距離が比例している場合 導線からの距離と、磁場との関係は、距離の2乗の反比例になる。 |
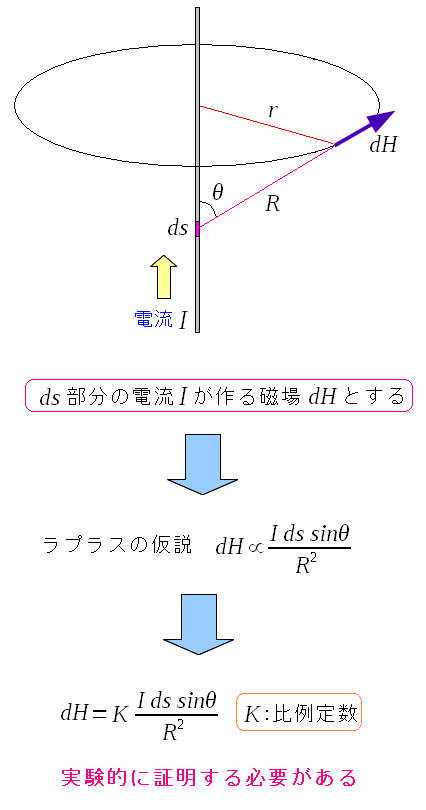
ここまでで、ビオサバールの法則の実験を知るための準備ができた。 1820年、ラプラスは以下の仮説を立てた。
| ラプラスの仮説(電流と磁場の関係) |
|---|
 |
|
電気素片(ds)を磁荷と考える。 ラプラスの仮説は、電気素片(ds)と、電気素片が作る磁場との関係式だ。 まさにビオサバールの法則の原型なのだ。 だが、この時点では思考段階であり、実験的に証明する必要がある。 |
そこでビオサバールが実験的に証明する事にした。 ところで、実験を行なう際、電流を流す導線に工夫をしているのだ。
| ビオサバールの実験。導線がV字型になっている |
|---|
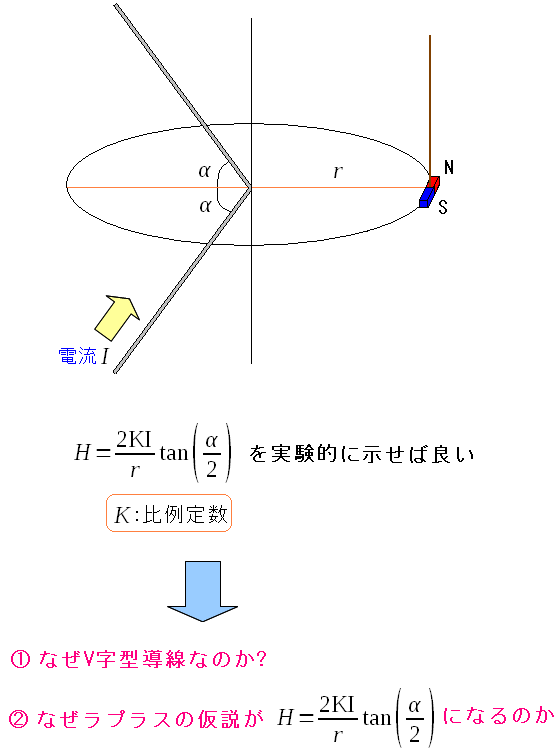 |
| 導線がV字型になっている。それには理由があるからだ。 |
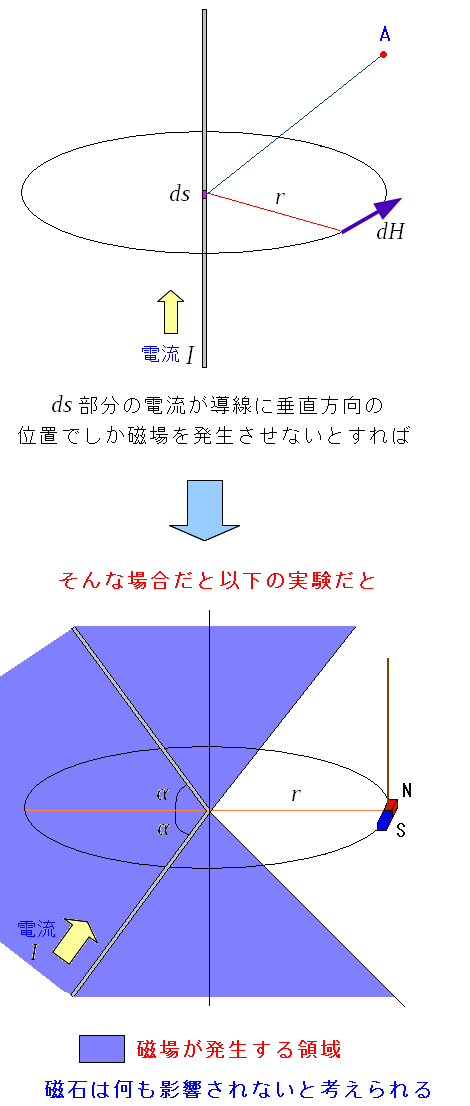
導線がV字型になっているのは、この当時、導線が発する磁場は 導線から垂直方向だけで発生していると考えられたからだ。
| 導線がV字型になっている理由 |
|---|
 |
|
導線を流れる電流素片(ds)が作る磁場が、導線の垂直方向しか磁場が発生せず 斜め方向の点Aでは、電流素片(ds)が磁場を作っていない場合が考えられる。 その場合、導線をV字型にしておく事で、磁石の位置では 電流が発生する磁場が来ないと考えられるので それを見極めるため、V字型にしているのだ。 |
すげー工夫やん!!
今でこそ、電気素片が作った磁場が、どういう振る舞いをするかが
わかっているので、導線をまっすぐにして実験すればエエやんと思うが
当時は、そんな事すら、わかっていなかったため、
1つ1つ調べていきながら、ビオサバールの法則に近づけていく様子が垣間見える。
| 何もかも手探りだった |
|---|
|
他にも磁力線の概念がなかった、安定した電流を流す技術もなかった。 そんな中で仮説を立てながら、工夫して実験を進めるのは凄い事だと思う。 |
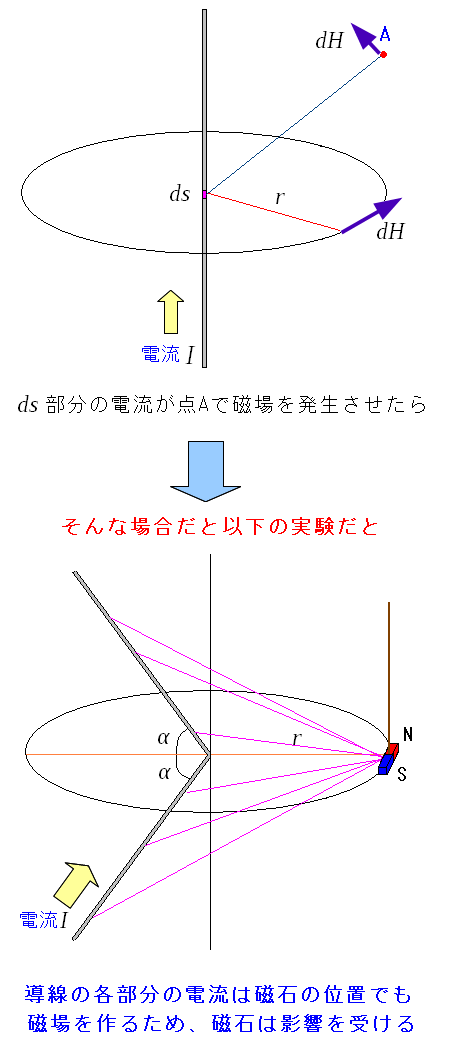
さて、電気素片が斜め方向にも磁場を作るとする。 その場合、導線がV字型であっても、電気素片が作る磁場は 磁石の位置でも磁場が発生するため、磁石に影響するのだ。
| 電気素片が斜め方向にも磁場を作る場合 |
|---|
 |
|
図にように、電気素片が斜め方向にも磁場を作る場合は 磁石がある場所にも磁場が発生するので、磁石は影響を受ける。 |
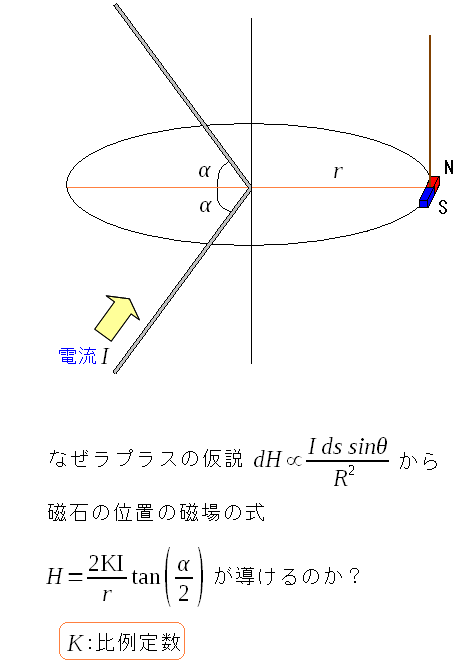
ラプラスの仮説の、電気素片が斜め方向にも磁場を作る場合の 電気素片と磁場との関係式を求めてみる。 その前に、なぜラプラスの仮説の式が求まるのか考えてみる。
| ラプラスの仮説の式 |
|---|
 |
|
導線をV字型にしているため、上図の式になっている。 なぜ、こういう式になるのか確かめる必要がある。 |
そこでラプラスの仮説の式を導いてみるのだ。
| ラプラスの仮説の式を導いてみる (下半分の導線を流れる電流が作る磁場) |
|---|
 |
| 下半分を流れる電流(電気素片)が作る磁場を求まった。 |
導線の下半分を流れる電流(電気素片)が作る磁場を求まった。 次に上半分を流れる電流(電気素片)が作る磁場を求めてみる。
| ラプラスの仮説の式を導いてみる (上半分の導線を流れる電流が作る磁場) |
|---|
 |
| 上半分を流れる電流(電気素片)が作る磁場を求まった。 |
下半分と上半分の合計を足すと、以下のようになる。
| ラプラスの仮説の式を導いてみる |
|---|
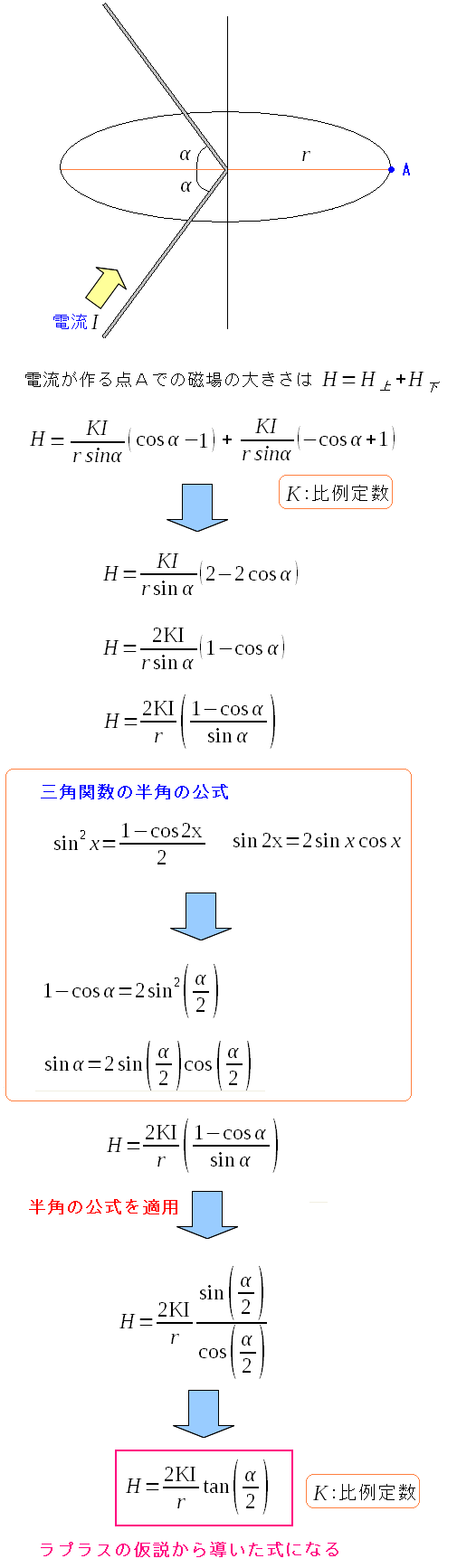 |
| ラプラスの仮説が導けたのだ。 |
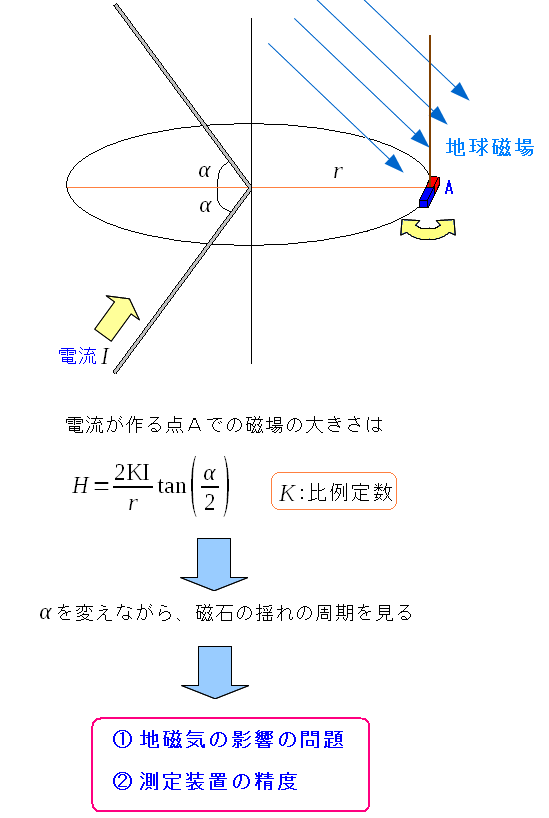
ラプラスの仮説が導けた所で、実際にビオサバールが実験したのだ。 この時、V字型の角度αを変えていく事で、同じ電流であっても 磁石の揺れ(周期)が変わったりする事で、電流と磁場との比例関係を 実験的に確かめる事ができるのだ。 ただ上の実験では、問題が残る。
| 実験における2つの問題点 |
|---|
 |
|
地磁気の影響だ。これは無視できない。 そして当時の実験器具の精度なのだ。 |
ビオサバールの法則が求まった。 まっすぐの無限に長い導線が作る磁場は以下のように求める事ができる。
| まっすぐの無限に長い導線が作る磁場 |
|---|
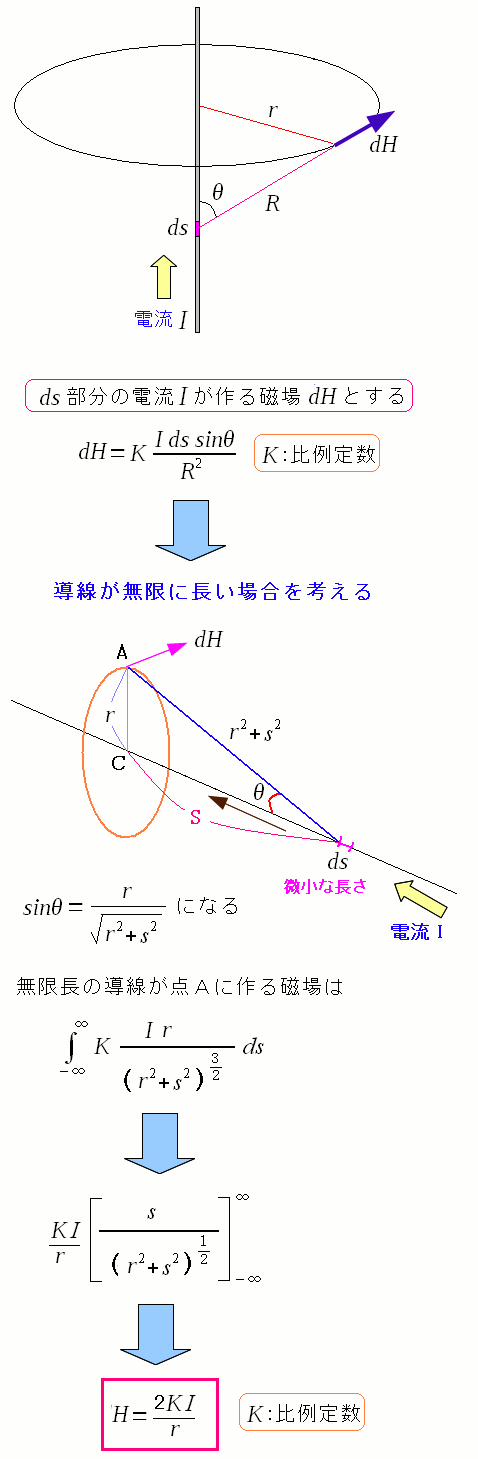 |
| 磁場の強さは、は電流の強さに比例し、導線からの垂直の距離に反比例するのだ。 |
現在では比例定数はわかっているので、改めてビオサバールの法則を書いてみた。
| ビオサバールの法則 |
|---|
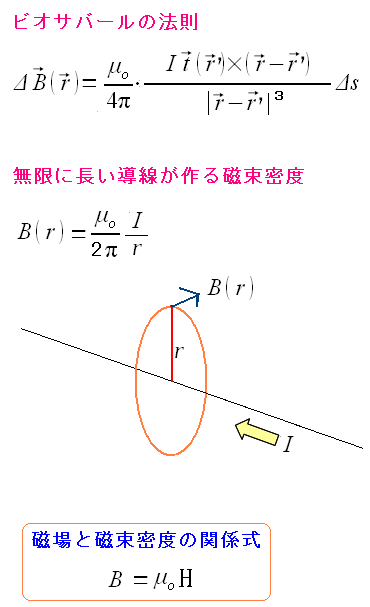 |
|
磁束密度(B)と電流素片との関係式なのだ。 ちなみに磁束密度(B)とは磁場(H)にμoを掛けた物なのだ。 |
円電流が発生する磁場
導線に電流を流すと磁場が発生する事がわかった。 では、導線を円状にした際、円の中心の磁場はどうなるのか? それを知る目的は、これから先に出てくる ソレノイドコイルを理解するため とか 磁気双極子を理解するための準備 なのだ。 最初に目的を書いていた方が勉強しやすい。 あとビオサバールの法則を使いこなす練習でもあるのだ。
| 円電流で発生する磁場は? |
|---|
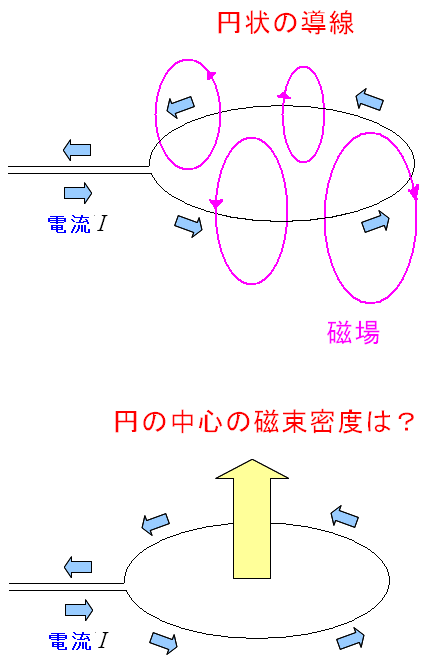 |
| ビオサバールの法則や右ネジの法則により 円状に導線に流れる電流によって、円を貫く磁場が発生する。 |
そこで円の中心を貫く磁束密度(磁場)の大きさを求めてみるのだ。
| 円の中心を貫く磁束密度 |
|---|
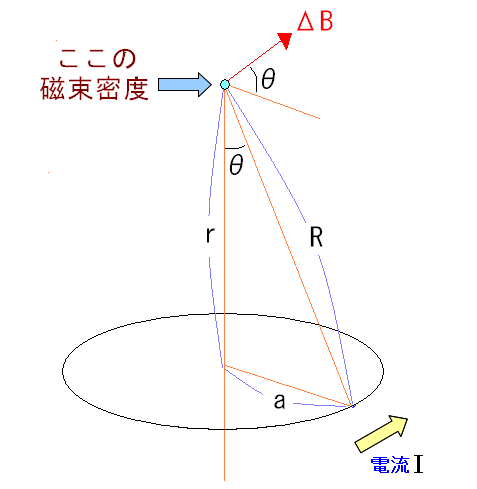 |
|
導線の電気素片が作る磁束密度の強さを求める。 求めたい磁場は、円の中心から垂直方向へrだけ移動した位置の磁場なのだ。 |
実際に計算してみる。
| 円の中心を貫く磁場を求めてみる |
|---|
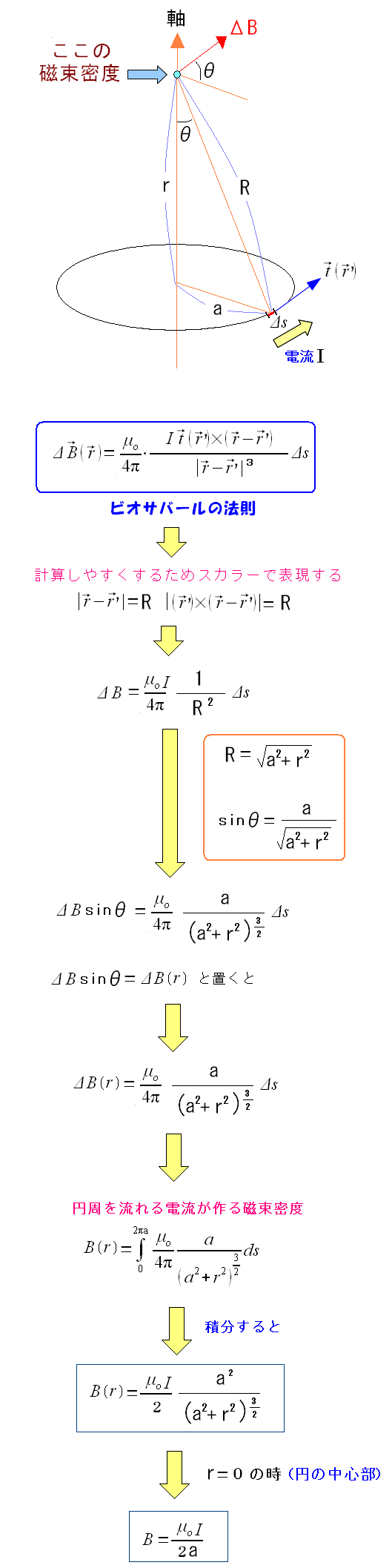 |
|
円の中心軸の位置(r)での磁束密度が求まったのだ。 ついでに、「r=0」の地点、円の中心での磁束密度も求めたのだ。 |
ところで円の中心軸上の磁束密度しか求めなかった。 他の場所に磁束密度になると・・・ 計算がめんどくさい!! という本音を出した所で、さっさと逃げることにする。
電磁気学入門の目次
| 電磁気学入門:目次 | |
|---|---|
| スカラーとベクトル | 簡単なスカラーとベクトルの話です。 ベクトルは方向と大きさを持つ量。方向という量持っているだけに注意が必要です。 |
| 静電気の発見からクーロンの法則 | 今でこそ当たり前の静電気や導体、絶縁体、電荷など どういう経緯で発見し、クーロンの法則まで至ったのかの話です。 |
| クーロン力、電場、近接作用 | 4つの力のうち、クーロン力の位置づけ 電荷が作り出す作用の電場。近接作用の話です。 |
| 微分、全微分、方向微分 | 簡単な微分、全微分、方向微分の話です。 ここをしっかり押さえないと、電磁気の数式の意味が わからなくなります。 |
| ベクトル解析 |
電磁気に必要なベクトル解析の話です。 勾配(grad)、2次元のグリーン定理 ストークスの定理の話です。 |
| 電位ポテンシャル | 電位ポテンシャルです。勾配と電場の関係を使って説明しています。 |
| 電気双極子 |
電気双極子の話です。 物質中で起こる分極を理解するのに必要です。 |
| ガウスの法則 | ガウスの法則の積分形、微分形の話です。 |
| ポアソンの方程式、ラプラス方程式 |
ポアソンの方程式、ラプラス方程式の話です。 単に電荷分布から電位を求めるだけの話にとどまらない 奥が深い分野です。ポテンシャル論、デルタ関数 グリーン関数、固有値問題について触れています。 |
| 静電場と渦なしの法則 |
静電場で、電荷を1周させた時の仕事はゼロ 微分形と微分形の渦なしの法則の話です。 |
| ビオサバールの法則 |
電気と磁場の関係の発見の話から ビオ・サバールの法則が導かれるまでの話です。 |
| 磁気双極子 |
磁気双極子の話で、回転電流になります。 物質中の磁場の話にも関連します。 |
| アンペールの法則 |
アンペールの法則の話です。 積分形・微分形だけでなく、閉回路に流れる電流が作る 磁気双極子の話なども書いています。 |
| ローレンツ力 |
磁場中を移動する電荷にかかる力(ローレンツ力)の話です。 ローレンツ力は相対性理論が絡んでいる事も紹介しています。 |
| ファラデーの誘導起電力の法則 | ファラデーの誘導起電力の話です。 |
| うず電流を使った簡単な物理実験 | 電力計に使われるアラゴの円盤。 そしてIH調理器で熱するために発生させる、うず電流は レンツの法則から電流が発生する原理を応用した物だ。 アラゴの円盤の実験と、IH調理器を使った実験です。 気分転換で読んでください。 |
| ベクトルポテンシャル |
わかりにくいベクトルポテンシャルの話です。 電位は電荷が作る電気のポテンシャルだが ベクトルポテンシャルは電流が作る磁場のポテンシャルの話です。 |
| オームの法則の微分形 | 微小領域でのオームの法則の話です。 |
| マックスウェルの方程式 |
4つのマックスウェルの方程式を書いています。 電場と磁場の変化を図にする事で rotの回転の意味も理解できます。 |
| ゲージ変換 |
ゲージ(gauge)は物差しの意味です。 マックスウェルの方程式をE(電場)とB(磁場)の関係式から φ(電位ポテンシャル)とA(ベクトルポテンシャル)の関係式に 書き換える際、ゲージ変換が使われます。 ゲージ変換の役目を書きました。 |
| 電磁波 |
マックスウェルの方程式から電波が伝わる様子を 視覚的に見てみる話です。 |
| 回転のrotはベクトルの微分 |
ベクトル解析や渦なしの法則で出てくるrotは ベクトルの微分という話です。 |
| 電磁気学の単位系 | 電磁気学の単位系の話です。 物理量の単位系の指数を見る次元解析 電磁気学の歴史と単位系の変遷について触れました。 |
| 電気泥棒:電気と法律の話 |
電気は物体なのか、無形物なのか。 明治時代に、電気を無断で使った場合、物か、そうでないかで 窃盗罪になるかどうかが裁判で問われました。 ちょっとした科学と法律の話です。気分転換で読んでください。 |
| 数ベクトルと基底ベクトル | ベクトルの話です。 矢印だけがベクトルでない事。 数ベクトルと基底ベクトルの違いの話です。 多様体、反変・共変ベクトルを理解するのに必要です |
| 多様体 | 空間を一般化した話です。 ▽(ナブラ)の正体に迫まります |
| 外積代数 |
外積、テンソルについて書いています。 極性ベクトル、軸性ベクトル 外積は行列で、ベクトルは見せかけの姿だった話です。 |
| ベクトルの双対関係 |
反変ベクトル、共変ベクトル、双対関係 ベクトル解析、外積代数の話 外積、テンソルについて書いています。 |
| ローレンツ力と相対性理論 |
磁場は電場の相対論的効果だった話です。 ローレンツ力を使って、導線が作る磁場を使って説明です。 |
| 微分形式 |
多様体の話の続きです。 座標に依存しない形での関数やベクトルの微分の話です。 ガウスの法則、アンペールの法則、マックスウェルの方程式が 鮮やかな形で表現できます。 ∇(ナブラ)の正体もわかります。 |
| 物理と対称性 |
マックスウェルの方程式をよく見ると対称性があります。 物理の方程式と対称性を数学的な観点でみると 意外なつながりがあるという話です。 |
| マックスウェルの応力 |
電気力線を弾性体(ゴム)とみなして、力の伝わり方などを 説明した考え方です。 |
| 電場エネルギー | 電場が持つエネルギーの式を導いた話です。 |
| 磁場エネルギー |
磁場が持つエネルギーの式です。 手抜きの説明と、直流RL回路を使った説明を書きました。 |
| ポインティングベクトル |
電磁エネルギーの流れ「ポインティングベクトル」の話です。 電磁波でもエネルギー保存則が成り立つ話から ポインティングベクトルを導いています。 |
| 電気エネルギーは導線の外を伝わる |
導線の外を電気エネルギーが流れる話です。 私が誤解した事、その誤解を解いていく過程を紹介しながら 「目からウロコ」にたどり着いた話です。 |
| 物質中の電場 | 物質中の電場の話です。 分極の話をしながら、物質中の電場の話をします |
| 物質中の磁場 | 磁性の話をしながら、物質中の磁場の話をします |
| 物質中のマックスウェルの方程式 | 物質中でもマックスウェルの方程式が成り立つ話です。 |
| 導体に侵入する電磁波 |
導体に侵入する電磁波が減衰していく話です。 表皮効果と同じ「表皮の厚さ」が出てきます |
| 表皮効果 |
目的の表皮効果の話です。 マックスウェルの方程式を解きながら 交流電流の周波数を上げると、表面にしか電流が流れなくなる話です。 |