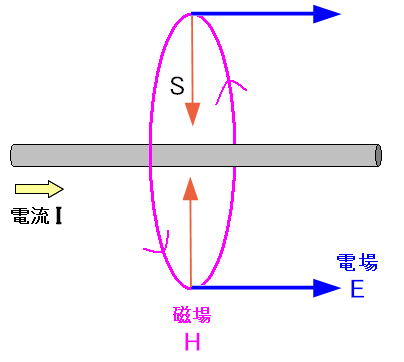
常に導線の外では、導線に並行した向きの電場が必要になる。
システム奮闘記:その105
(2016年5月22日に掲載)
はじめに ポインティングベクトルの話の部分で、電気エネルギーは電線の外を伝わる事に触れた。 電流のエネルギーは電線の外を伝わる!(松田卓也先生「教科書の教えてくれない物理」第1回 | 大学ジャーナル) ところで電気エネルギーは導線の外では、どうやって伝わるのか? 電磁気の事を正しく理解していれば、意外と簡単に「なるほど」となるのだが、 私の場合、正しく理解していなかったため、七転八倒したり トンデモ科学みたいな解釈をしてしまいそうになったのだ。 ここでは、私が誤解しながらも、理解に達した話をしながら 電気エネルギーが電線の外を伝わる事を説明していくことにした。
トンデモ科学に走る私
常に導線の外部からエネルギーを取り込んでいる。 となれば、外部から内部へエネルギーを運ぶため・・・ 導線の外も、導線と同じ向きの電場が必要 になってくる。
| 導線の外も、導線と同じ向きの電場が必要 |
|---|
 |
|
導線の外からエネルギー供給する場合 常に導線の外では、導線に並行した向きの電場が必要になる。 |
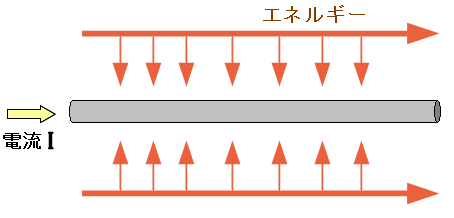
そして電気エネルギーは導線の外を伝わるため 導線と並行した向きでエネルギーが伝わっていると考える。
| 導線と並行した向きでエネルギーが伝わっていると考える(私の仮説) |
|---|
 |
|
電気エネルギーは導線の外を伝わるため エネルギーの流れは、導線と並行の向きに流れていると考えた。 (誤解を招かないためのお断り) あくまでも私が思い浮かんだ話です。 実際には、異なる形で伝わっています。後述しています。 |
そして・・・
トンデモ科学を思いつく私
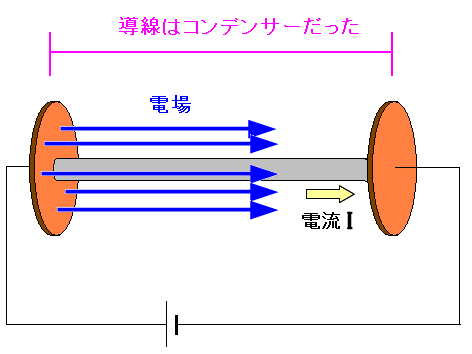
常に導線外部からエネルギーを供給するためには
導線と並行した向きに電場があると考えた。
| 導線はコンデンサーだった(私の仮説・トンデモ科学) |
|---|
 |
|
コンデンサーは電極の中に誘導体をはさんでいる。 導線を誘導体を考え、周囲の空間も電極板が重なっている部分があり そこから電場が流れていると考えてみた。 だが、この場合、導線が曲がっていると、すぐに崩れ去る妄想だった。 |
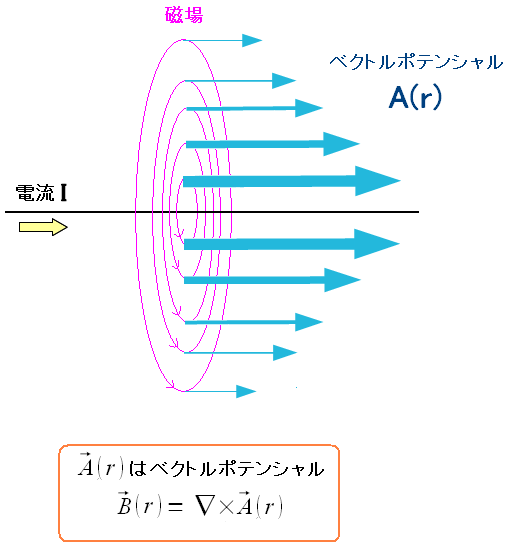
エネルギーは導線の外を伝わる。 ふと思った。 ベクトルポテンシャルは導線の外を伝わっている。
| 電流とベクトルポテンシャルの関係 |
|---|
 |
|
ベクトルポテンシャルは、電流が作る位置エネルギーと言われる。 そして電流(導線)と一緒の方向に進んでいる。 |
もしかして
ベクトルポテンシャルで電気エネルギーを運んでいるのでは
と考えつく。
| ベクトルポテンシャルで電気エネルギーを運んでいる(私の仮説・トンデモ科学) |
|---|
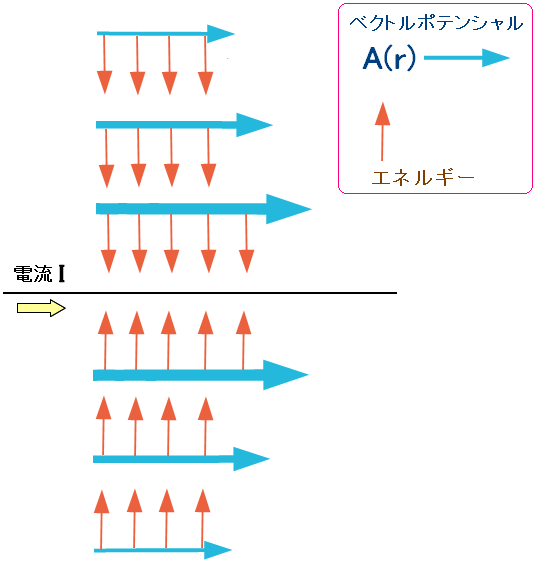 |
| 全然、電磁気を理解していないため、仮説ではなく妄想だ。 |
完全に トンデモ科学と妄想 の世界になったのだ。
ポインティングベクトル
トンデモ科学に走ったが軌道修正しないと具合が悪い。 大学教授なら「権威」があるので、マスコミは面白がって取り上げるが 私が言っても・・・ ただのアホなオッサン になってしまう。 そこでネットを検索したり、書店や図書館へ行き、真相を探しまくった。 以下の本が見つかった。 「電磁波の物理-その発生・伝播・吸収・増幅・共振を電磁気学で理解する」(遠藤雅守:森北出版) この本に書いている内容を見て固まってしまった。
| 回路の中のポインティングベクトル |
|---|
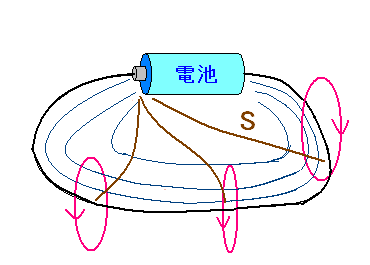 |
|
ポインティングベクトルはエネルギーの流れ。 導線の側を電場(青い等高線?)があり、それに垂直になるような感じで 導線内に入っていく感じだ だが、詳しい解説がなかったので、目が点になるしかなかった。 |
もう理解の限度を越えとる・・・ 万事休すと思った。 だが、一発で理解できる物を見つけた ◆◆ 科学カフェ京都 第69回 定例会 ◆◆ (松田卓也(宇宙物理学)|科学カフェ京都(特定非営利活動法人) 京都カフェの「電流のエネルギーは電線の外を流れる」の講演動画も公開しているのだ。 講演ビデオ:http://www.kagakucafe.org/matsuda101216.wmv(WMV形式) これを見ると・・・ 目からウロコ なのだ。 めちゃくちゃ噛み砕いて説明されているので、非常にわかりやすい。 導線中の電場は、電気エネルギーを運ばない だった。 松田卓也さんは超伝導を例に説明されている。
| 超伝導体は電気抵抗がゼロ |
|---|
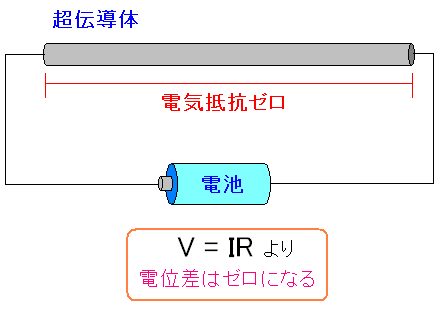 |
|
超伝導体は電気抵抗はゼロ。 電位差を求める際、「電流×抵抗=電位」になるのだが 超伝導体の両端の電位差はゼロになる。 |
全然、気づかなかったが、言われると納得する。
| 超伝導体は電位差がゼロ |
|---|
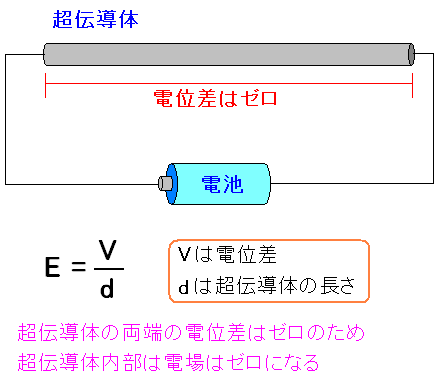 |
|
超伝導体の両端では電位差はゼロ。 「電場=電位÷距離」なので、超伝導体の電場はゼロになる。 |
そのため超伝導内部では電気エネルギーが流れないのだ。
| 超伝導内部では電気エネルギーが流れない |
|---|
 |
|
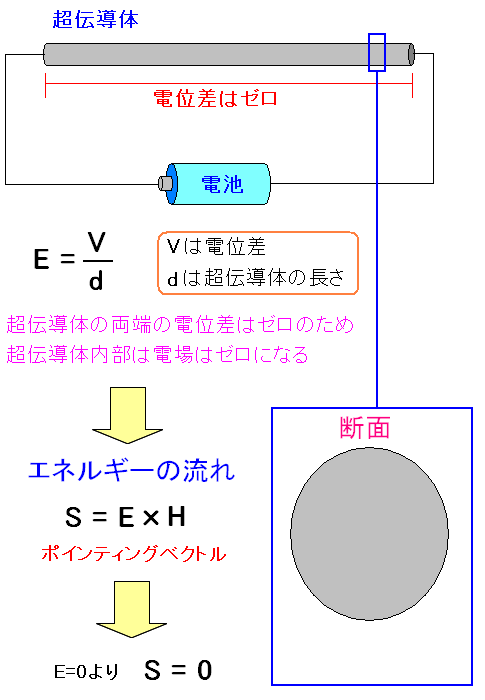
超伝導内部では電場がゼロだ。 電磁エネルギーの流れはポインティングベクトルだ。 「ポインティングベクトル=電場×磁場」の式だ。 電場はゼロなので、導線内のポインティングベクトルもゼロになる。 つまり超伝導内部では電磁エネルギーの流れはゼロなのだ。 |
だが、超伝導体は電気抵抗ゼロで無限に電気を流す夢の素材であり 超伝導送電を行なえば、送電損失がなくなると言われている。
| 超伝導体は電気抵抗ゼロで無限に電気を流す |
|---|
 |
|
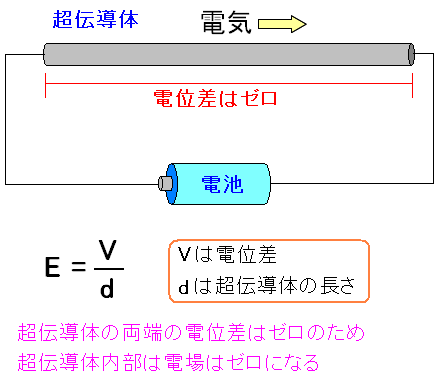
超伝導内部では電磁エネルギーの流れはゼロである事は 電気エネルギーは超伝導体の導線の外を伝わる事が言える。 |
こんな話は・・・ 全く想像もつかへんかった!! なのだ。 言い換えると・・・ 電磁気を勉強したが、全然、理解してへん 事が証明されてしまったのだ。 ふと気づいた。 超伝導体の内部には電場がないという事は、超伝導体内部は電流が流れていないのでは・・・ 調べてみたのだが、私の頭で理解できる形で説明しているサイトや資料は 見つからなかった。 超伝導は量子力学を知らないと理解できない分野なので 物性物理や超伝導の研究を考えている学生さんは 超伝導体の内部で電流が流れているかどうか、確かめて欲しいのだ。ポインティングベクトルと抵抗・ジュール熱
松田卓也さんの話は続く。 抵抗がある導線の話 になった。
| 抵抗がある普通の導線 |
|---|
 |
|
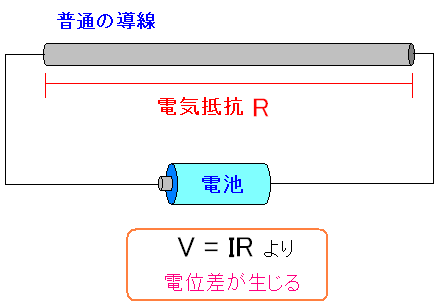
導線の電気抵抗をRとした。 電位差を求める際、「電流×抵抗=電位」になる 電流Iが流れると、電位差がVというわけだ。 |
電位差が生じる事は電場が生じる事と同じなのだ。
| 抵抗がある普通の導線内部では電場が発生する |
|---|
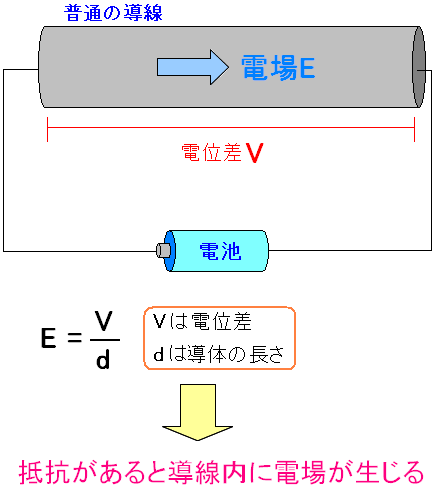 |
| 「電場=電位÷距離」なので、導体の電場は存在する。 |
導線内で発生した電場が厄介な事をするというのだ。 導線表面に着目する。
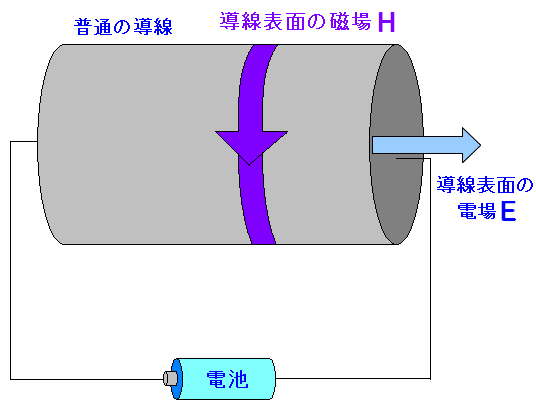
| 導線の表面には電場と磁場がある |
|---|
 |
|
電位差がある所に電場がある。 導体内は電流が流れているので、アンペールの法則により磁場がある。 |
導線の表面にある電場と磁場。 お互い直角の方向になっている。 するとポインティングベクトルの方向が導線の内側になるのだ。
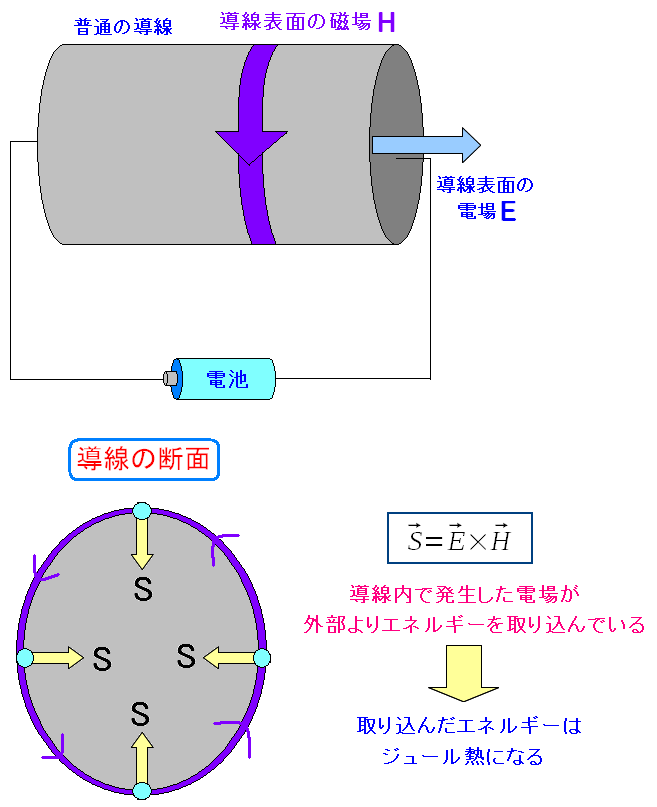
| ポインティングベクトルの方向が導線の内側になる |
|---|
 |
|
外から電磁エネルギーが流入する形になる。 そのエネルギーは導体内の分子運動や電子の運動になり それが熱になってしまうのだ。ジュール熱だ。 抵抗がある所に電位あり。電位ある所に電場あり。 電流が流れている所に磁場があり。 電場と磁場があるから、外部からエネルギーを取り込み熱になる。 オームの法則で電気抵抗とジュール熱に触れたのだが、これが抵抗の正体なのだ。 |
電気エネルギーが伝わる仕組み
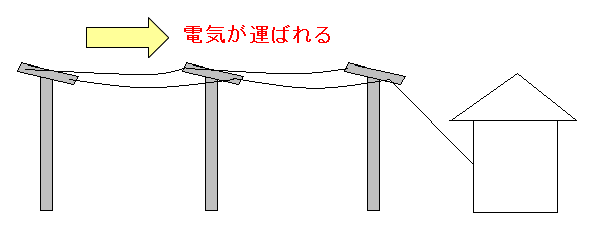
では、ここで疑問が浮かぶ。 外部から電気エネルギーを取り込んでいるのだが そもそも電気エネルギーは どないして導体表面まで運ばれてるねん? 松田卓也さんのわかりやすい講義のお陰で、それも目からウロコだった。 家庭用電気は、電柱にある電線から運ばれる。
| 家庭用電気は、電柱にある電線から運ばれる |
|---|
 |
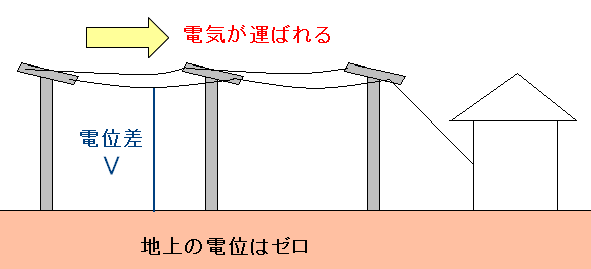
松田卓也さんの講義のお陰で、ある事に気づいた。 電柱の電線と地面との間では 電位差が生じているやん!!
| 電柱の電線と地面との間では電位差が生じる |
|---|
 |
|
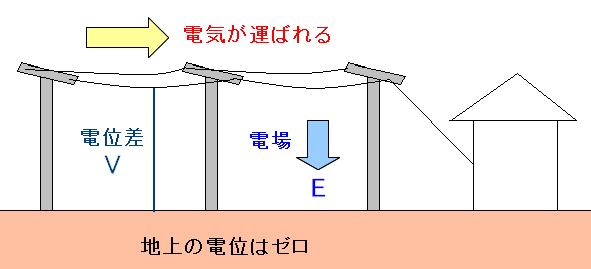
地上の電位はゼロとする。 電線には電気を流しているので電位が高くなっている。 |
そして「電位=電場×距離」なのだ
電位のある所に電場あり
という事で、電線から地上に向けて電場が流れているのだ。
| 電線から地上に向けて電場が流れている |
|---|
 |
|
この事は、今まで気づかなかった。 私が電磁気の本質を理解していなかった証拠なのだ。 |
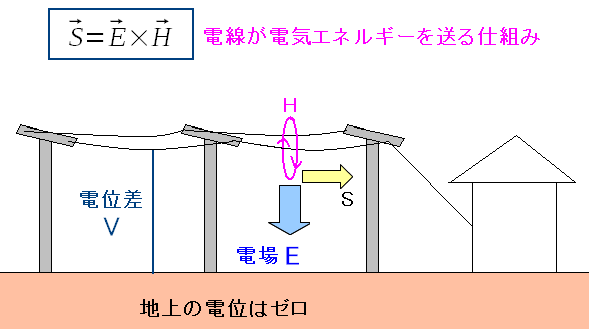
そしてポインティングベクトルは「電場×磁場」だ。
| ポインティングベクトルは送電方向に向いている |
|---|
 |
|
電位ゼロの地表に向う電場と、送電の電流が作る磁場(アンペールの法則)が 電線に沿って電気エネルギーを運搬するポインティングベクトルになっている。 |
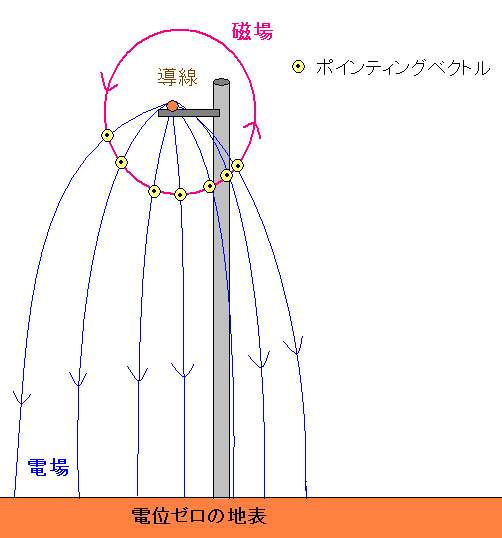
これだけだと、わかりにくいので断面図を見てみる。
| ポインティングベクトルは送電方向に向いている(断面) |
|---|
 |
|
電位ゼロの地表に向う電場と、送電の電流が作る磁場(アンペールの法則)が 電線に沿って電気エネルギーを運搬するポインティングベクトルになっている。 |
これが電気エネルギーを送る仕組みだったのだ。 全く考えもしなかった。 驚きで言葉にならへん!! 感覚と事実が一致しない現象だ。 書店で見たノーベル賞受賞者のファインマンの本にも書いていた。 「ファインマン物理学<4>電磁波と物性」(ファインマン:岩波書店) この奇妙な理論によれば・・・ ファインマン自身も感覚的には違和感があるという事だろうか。 原文だと「Crazy」らしく、もっと過激になっているらしいが・・・。 電気回路で見てみる。 電柱の電線と違って、周回している回路になっている。 この場合、ポインティングベクトルがどうなっているのか見てみるのだ。 と松田卓也さんの講義の受け売りを書いてみる。
| 抵抗だけがある簡単な電気回路 |
|---|
 |
|
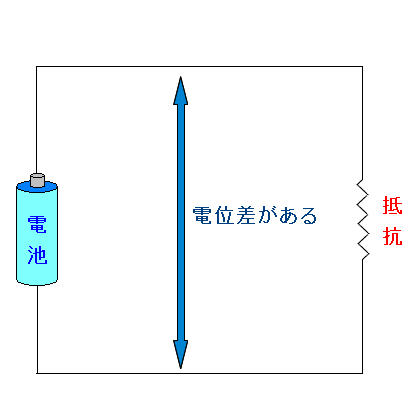
四角形の回路で考える。 抵抗の前後には電位差がある。 導線同士でも電位差があるのだ。 |
お馴染みになった
電位がある所に電場あり
なので回路内には、以下の電場になっている。
| 四角形の回路の電場の様子 |
|---|
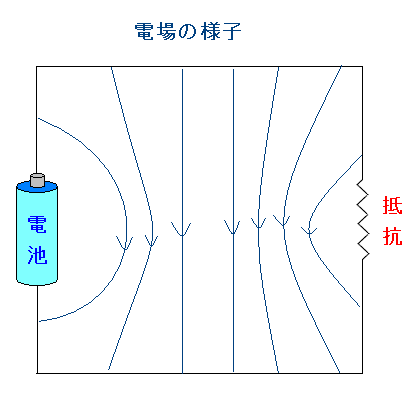 |
| 松田卓也さんの講義を見るまでは、考えもしなかった事だ。 |
そして電流が流れているので、アンペールの法則より 電流の周囲には磁場が発生している。
| 電流の周囲には磁場が発生している |
|---|
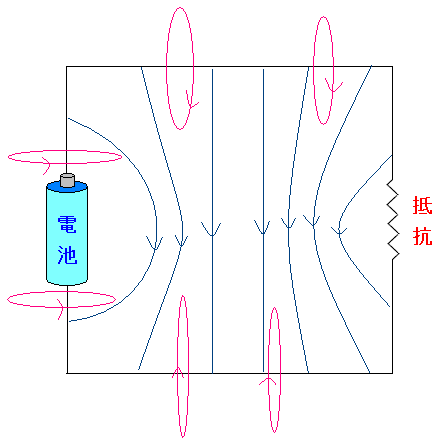 |
| 導線を軸に円形の磁場が発生しているのだ。 |
ポインティングベクトルを求めてみる。
| 四角形の回路のポインティングベクトル |
|---|
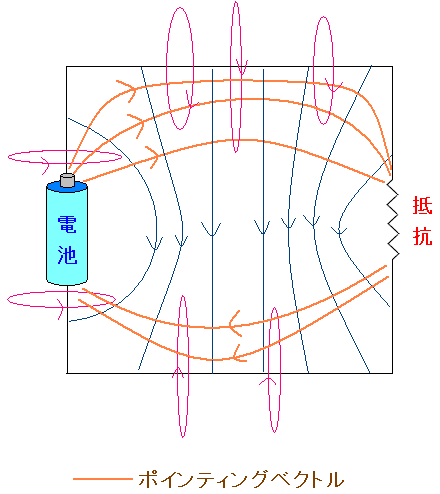 |
|
「電場×磁場」で、電場と磁場に垂直の向きになっている。 空間を越えて伝わっている。 書店で見た以下の本の図と同じになっている。 「電磁波の物理-その発生・伝播・吸収・増幅・共振を電磁気学で理解する」(遠藤雅守:森北出版) |
電気エネルギーは導線でなく空間を飛んでいく
感覚と事実との不一致だ。信じられない。
だが、事実なので受け入れるしかないし、ファインマンだって
「この奇妙な理論」と言いつつ、「電気エネルギーは空間を飛んでいく」と教えているのだ。
最後に、松田卓也さんが出してきた話が面白かった。
以下の回路で、一番最初に電球が点灯するのはどれという問題だ。
| 一番最初に点灯するのは、どの電球か? |
|---|
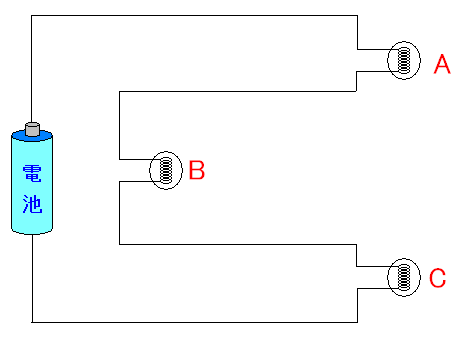 |
|
普通に考えると「A→B→C」と答えそうなのだが、電源に一番近いのはB。 松田卓也さんは「Bだと思う」だった。 100年以上前にポインティングさんによって提唱された ポインティングベクトル。でも、謎に満ちた感じがするものだ。 |
ただ、松田卓也さんの講演で、真偽が定かでないと思った事はある。 松田卓也さんは講演の中で 電気エネルギーが伝わるのが導線の内か外かを質問した所 電気工学の先生も結構、わかっとらん だった。 本当だったら、大学の先生でも理解していないのだから 私が理解していなくても当然 と胸を張って言えるのだが、ちょっと信じがたい話な上 真偽は定かでないので、何とも言えない。 松田卓也さんの毒舌が炸裂する。
| 松田卓也さんの毒舌(?) | |
|---|---|
| (1) | 科学は本質がわかってなくても教えられる。 |
| (2) |
物理がわかっていなくても論文は書ける。 式を変形すれば論文は書けるから |
| (3) | 物事は真実を理解していなくても教えられる。 |
専門家でなくても、社会人だと耳の痛い話なのだ。
| 学生さんに助言 |
|---|
|
就職活動などで、「君達は社会を知らない」とか 「学生はヒヨっ子」という態度で接する面接官がいたりする。 だが、案外、社会人も、物事の本質を知らずに仕事をしていたりする。 IT分野でも、情報理論や情報科学を知らないで、マニュアルに書かれた事だけで 作業する人達もいるし、それで仕事ができてしまったりする。 私も偉そうな事はいえない。手法や方法は知っていても その背景にある原理、理論を知らない事の方が多いのだ。 面接の際、面接官が嫌がる質問をして「あんたも、わかってへんやん」と言える 学生は頼もしいと思う。ただ、それで面接に落ちても、私は責任は取れないが・・・ |
磁場中に静止した荷電粒子のエネルギー
ポインティングベクトルの話。まだ続きがある。 ファインマンの本には次の事も書いていた。 磁場中に静止した荷電粒子を置いた場合 ポインティングベクトルはどうなっているのか だった。 全く考えもしなかった。
| 磁場中に荷電粒子を置いてみる |
|---|
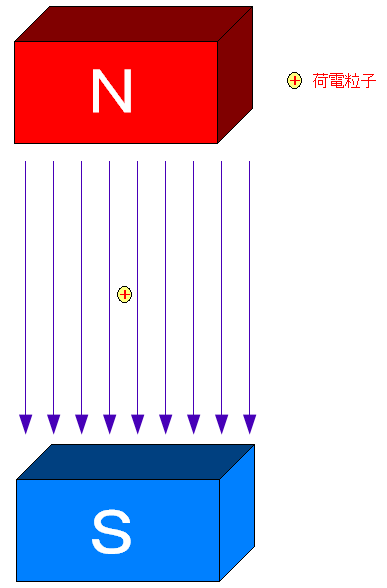 |
| 磁場中に静止した荷電粒子を置いても何も起こらない。 |
荷電粒子は電場を発している。
| 荷電粒子は電場を発している |
|---|
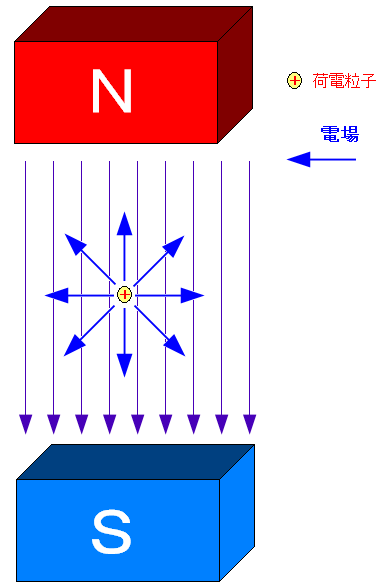 |
| 荷電粒子は電場を発している。 |
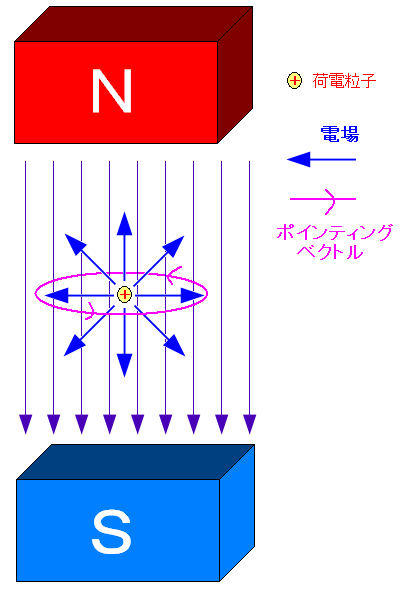
電場と磁場がある所には、エネルギーの流れである ポインティングベクトルが存在する。
| 静止した荷電粒子の周囲をポインティングベクトルが回転する |
|---|
 |
|
荷電粒子の周囲をエネルギーの流れである ポインティングベクトルが走っている。 |
もちろん、エネルギーの流れは1つだけではない。
| 静止した荷電粒子の周囲のエネルギーの流れ |
|---|
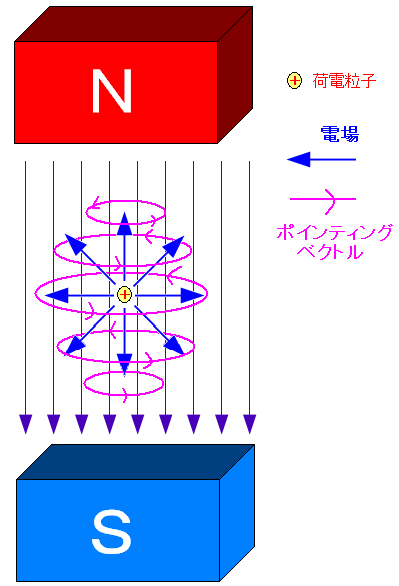 |
| 荷電粒子を覆う形で、エネルギーの流れが発生している。 |
このエネルギー何のエネルギーやねん!! と思った。 だが、物性物理や量子力学の知識がないため、踏み込んで調べるのは断念したのだ
電磁気学入門の目次
| 電磁気学入門:目次 | |
|---|---|
| スカラーとベクトル | 簡単なスカラーとベクトルの話です。 ベクトルは方向と大きさを持つ量。方向という量持っているだけに注意が必要です。 |
| 静電気の発見からクーロンの法則 | 今でこそ当たり前の静電気や導体、絶縁体、電荷など どういう経緯で発見し、クーロンの法則まで至ったのかの話です。 |
| クーロン力、電場、近接作用 | 4つの力のうち、クーロン力の位置づけ 電荷が作り出す作用の電場。近接作用の話です。 |
| 微分、全微分、方向微分 | 簡単な微分、全微分、方向微分の話です。 ここをしっかり押さえないと、電磁気の数式の意味が わからなくなります。 |
| ベクトル解析 |
電磁気に必要なベクトル解析の話です。 勾配(grad)、2次元のグリーン定理 ストークスの定理の話です。 |
| 電位ポテンシャル | 電位ポテンシャルです。勾配と電場の関係を使って説明しています。 |
| 電気双極子 |
電気双極子の話です。 物質中で起こる分極を理解するのに必要です。 |
| ガウスの法則 | ガウスの法則の積分形、微分形の話です。 |
| ポアソンの方程式、ラプラス方程式 |
ポアソンの方程式、ラプラス方程式の話です。 単に電荷分布から電位を求めるだけの話にとどまらない 奥が深い分野です。ポテンシャル論、デルタ関数 グリーン関数、固有値問題について触れています。 |
| 静電場と渦なしの法則 |
静電場で、電荷を1周させた時の仕事はゼロ 微分形と微分形の渦なしの法則の話です。 |
| ビオサバールの法則 |
電気と磁場の関係の発見の話から ビオ・サバールの法則が導かれるまでの話です。 |
| 磁気双極子 |
磁気双極子の話で、回転電流になります。 物質中の磁場の話にも関連します。 |
| アンペールの法則 |
アンペールの法則の話です。 積分形・微分形だけでなく、閉回路に流れる電流が作る 磁気双極子の話なども書いています。 |
| ローレンツ力 |
磁場中を移動する電荷にかかる力(ローレンツ力)の話です。 ローレンツ力は相対性理論が絡んでいる事も紹介しています。 |
| ファラデーの誘導起電力の法則 | ファラデーの誘導起電力の話です。 |
| うず電流を使った簡単な物理実験 | 電力計に使われるアラゴの円盤。 そしてIH調理器で熱するために発生させる、うず電流は レンツの法則から電流が発生する原理を応用した物だ。 アラゴの円盤の実験と、IH調理器を使った実験です。 気分転換で読んでください。 |
| ベクトルポテンシャル |
わかりにくいベクトルポテンシャルの話です。 電位は電荷が作る電気のポテンシャルだが ベクトルポテンシャルは電流が作る磁場のポテンシャルの話です。 |
| オームの法則の微分形 | 微小領域でのオームの法則の話です。 |
| マックスウェルの方程式 |
4つのマックスウェルの方程式を書いています。 電場と磁場の変化を図にする事で rotの回転の意味も理解できます。 |
| ゲージ変換 |
ゲージ(gauge)は物差しの意味です。 マックスウェルの方程式をE(電場)とB(磁場)の関係式から φ(電位ポテンシャル)とA(ベクトルポテンシャル)の関係式に 書き換える際、ゲージ変換が使われます。 ゲージ変換の役目を書きました。 |
| 電磁波 |
マックスウェルの方程式から電波が伝わる様子を 視覚的に見てみる話です。 |
| 回転のrotはベクトルの微分 |
ベクトル解析や渦なしの法則で出てくるrotは ベクトルの微分という話です。 |
| 電磁気学の単位系 | 電磁気学の単位系の話です。 物理量の単位系の指数を見る次元解析 電磁気学の歴史と単位系の変遷について触れました。 |
| 電気泥棒:電気と法律の話 |
電気は物体なのか、無形物なのか。 明治時代に、電気を無断で使った場合、物か、そうでないかで 窃盗罪になるかどうかが裁判で問われました。 ちょっとした科学と法律の話です。気分転換で読んでください。 |
| 数ベクトルと基底ベクトル | ベクトルの話です。 矢印だけがベクトルでない事。 数ベクトルと基底ベクトルの違いの話です。 多様体、反変・共変ベクトルを理解するのに必要です |
| 多様体 | 空間を一般化した話です。 ▽(ナブラ)の正体に迫まります |
| 外積代数 |
外積、テンソルについて書いています。 極性ベクトル、軸性ベクトル 外積は行列で、ベクトルは見せかけの姿だった話です。 |
| ベクトルの双対関係 |
反変ベクトル、共変ベクトル、双対関係 ベクトル解析、外積代数の話 外積、テンソルについて書いています。 |
| ローレンツ力と相対性理論 |
磁場は電場の相対論的効果だった話です。 ローレンツ力を使って、導線が作る磁場を使って説明です。 |
| 微分形式 |
多様体の話の続きです。 座標に依存しない形での関数やベクトルの微分の話です。 ガウスの法則、アンペールの法則、マックスウェルの方程式が 鮮やかな形で表現できます。 ∇(ナブラ)の正体もわかります。 |
| 物理と対称性 |
マックスウェルの方程式をよく見ると対称性があります。 物理の方程式と対称性を数学的な観点でみると 意外なつながりがあるという話です。 |
| マックスウェルの応力 |
電気力線を弾性体(ゴム)とみなして、力の伝わり方などを 説明した考え方です。 |
| 電場エネルギー | 電場が持つエネルギーの式を導いた話です。 |
| 磁場エネルギー |
磁場が持つエネルギーの式です。 手抜きの説明と、直流RL回路を使った説明を書きました。 |
| ポインティングベクトル |
電磁エネルギーの流れ「ポインティングベクトル」の話です。 電磁波でもエネルギー保存則が成り立つ話から ポインティングベクトルを導いています。 |
| 電気エネルギーは導線の外を伝わる |
導線の外を電気エネルギーが流れる話です。 私が誤解した事、その誤解を解いていく過程を紹介しながら 「目からウロコ」にたどり着いた話です。 |
| 物質中の電場 | 物質中の電場の話です。 分極の話をしながら、物質中の電場の話をします |
| 物質中の磁場 | 磁性の話をしながら、物質中の磁場の話をします |
| 物質中のマックスウェルの方程式 | 物質中でもマックスウェルの方程式が成り立つ話です。 |
| 導体に侵入する電磁波 |
導体に侵入する電磁波が減衰していく話です。 表皮効果と同じ「表皮の厚さ」が出てきます |
| 表皮効果 |
目的の表皮効果の話です。 マックスウェルの方程式を解きながら 交流電流の周波数を上げると、表面にしか電流が流れなくなる話です。 |