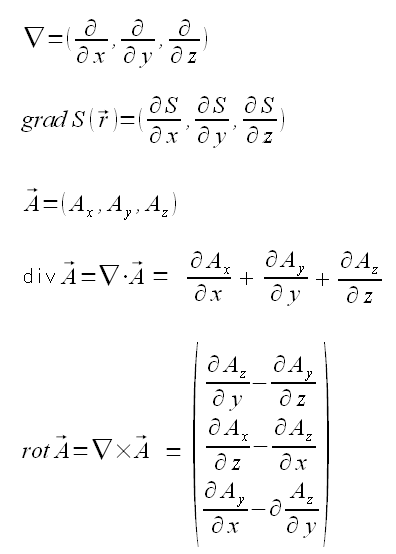
ベクトル解析の本が補助として必要になってくる。
システム奮闘記:その105
(2016年5月22日に掲載)
数学の知識が必要なわけ
電磁気学を勉強する際、数学の知識が必要だ。 数式とは 現象を定量的に表現するための言語 だからだ。 大きさや強さの度合といった「量」が大事になる。 どれくらいの量の物質があると、どれくらいの力の量が働くのか。 それを記述するために数式があるのだ。 なので数学を理解せずに、式の丸暗記や、出てきた数式の意味を知らずに 電磁気学を勉強しても、物理現象の表現が理解できないため 途中で、わけがわからんようになるのだ。 偉そうに書いたのだが、実は・・・ 七転八倒して得た体験則なのだ (^^;; 表皮効果を調べるためには、電磁気学の基本を理解が必要だ。 そのためには、ベクトル解析をはじめ、微積分の知識も必要になってくる。
| いくつかの数式 |
|---|
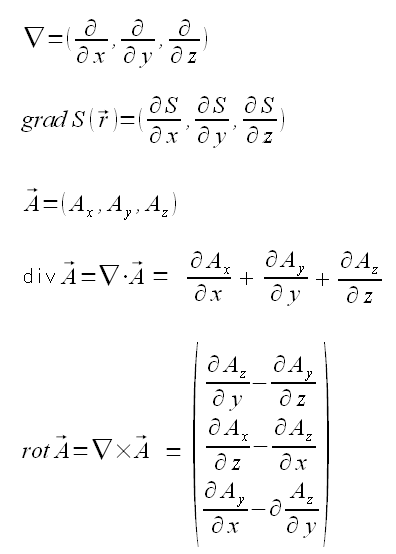 |
|
電磁気学に出てくる数式だ。 ベクトル解析の本が補助として必要になってくる。 |
だが、数学を勉強をしていたのは20世紀の話。 今では忘却の彼方なので こんな数式なんて忘れてもうた なのだ。 そこで復習しながら、思い出していく事にした。
微分
まずは高校で習う微分の復習から行なう。 平たく言えば、以下の説明になる。
| 微分とは何か? |
|---|
 |
|
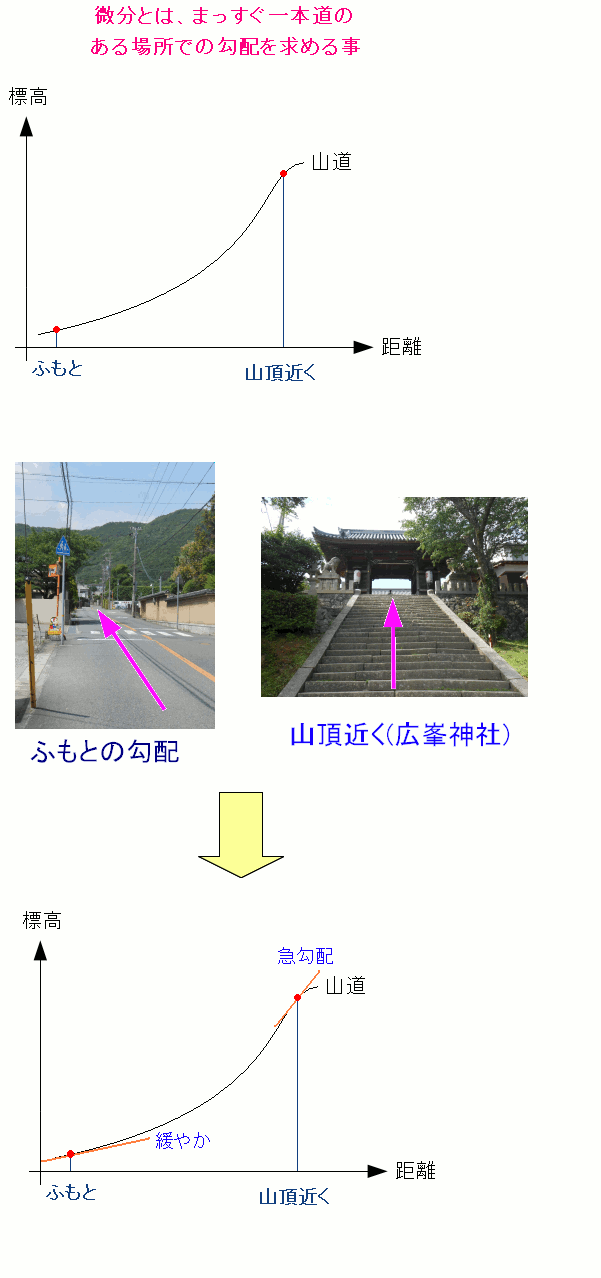
1本道の話だとわかりやすい。 まっすぐな道でも、山を通ったり、谷を通ったりする。 ある地点での勾配を求めるのが微分という作業だ。 上の例だと、ふもとでの勾配と、山頂付近での勾配だ。 ふもとでの勾配は緩やかで登りやすい。 だが山頂では勾配は急なので登ると息が切れる。 (余談) 広峯神社といえば、2014年の大河ドラマ「黒田官兵衛」のロケ地だ。 南沢奈央ちゃんが演じる・官兵衛の初恋の役の「おたつ」が住んでいた所だ。 神社には、ドラマで黒田重隆が財をなしたという黒田家に代々伝わる 目薬の木も植えている。姫路に来られた際は、広峯神社もお勧めします!! |
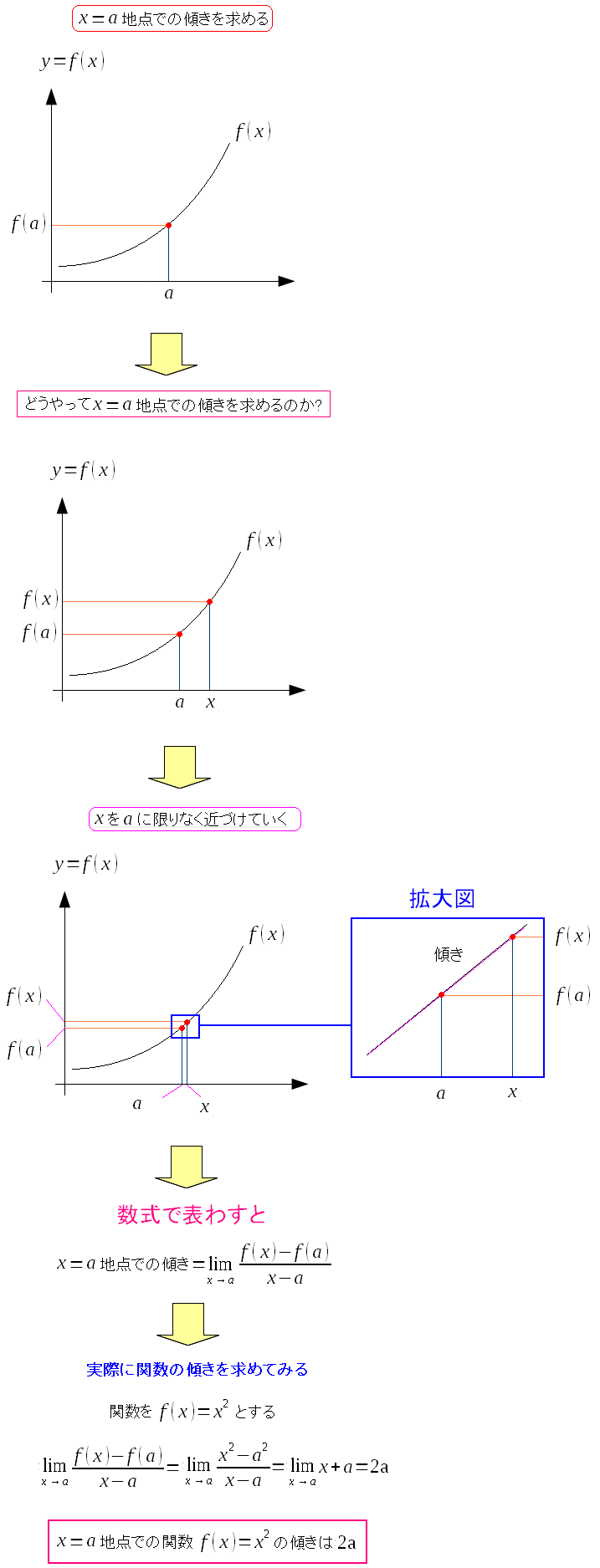
微分が勾配を求める事だとわかった所で、実際に数学的な視点から 1変数の関数f(x)を用意して、x=a地点での関数の傾きを求めてみるのだ。
| 関数の傾きを求めてみる |
|---|
 |
|
勾配は傾きだが、まさに傾きは変化の割合なのだ。 その点での微分とは、その地点での傾き(関数の変化の割合)を求める事になる。 |
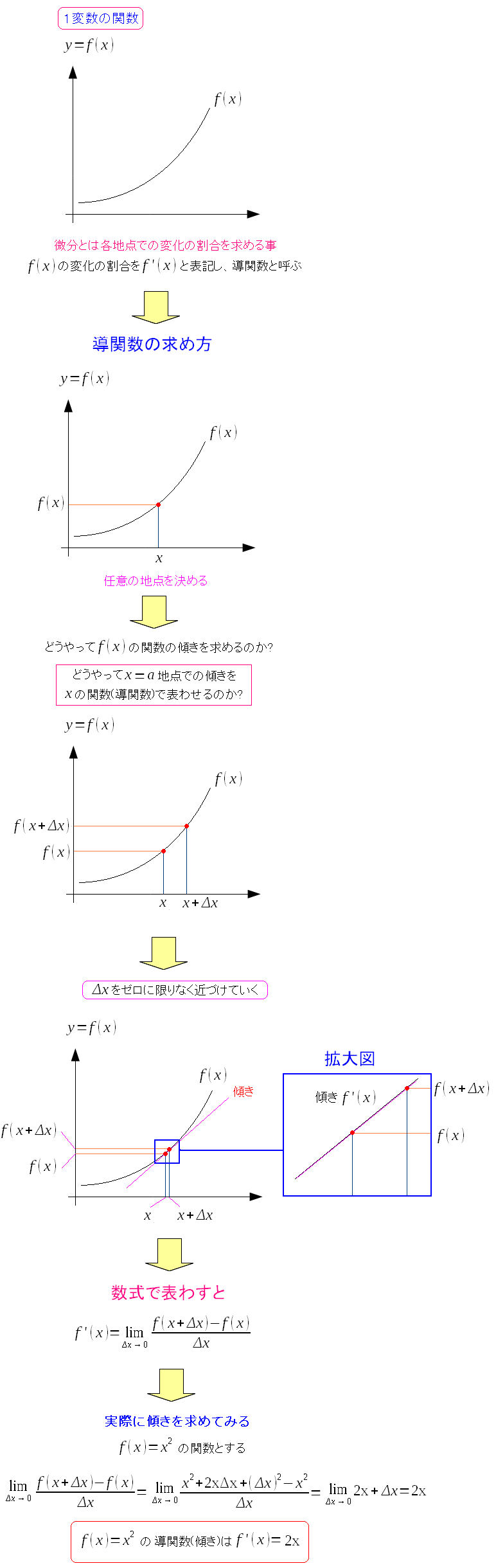
傾きを求める際、一般化したい。 任意の位置xの地点での、関数f(x)の傾きの関数で表わしてみる。
| 関数の傾きである導関数を求めてみる |
|---|
 |
|
先ほどは x=aの地点での関数f(x)の傾きを求めたが 今回は、任意の位置での関数の傾きである導関数を求めたのだ。 |
関数から導関数を求める事を
微分する
というのだ。
任意の位置での導関数を求める方法がわかったので、
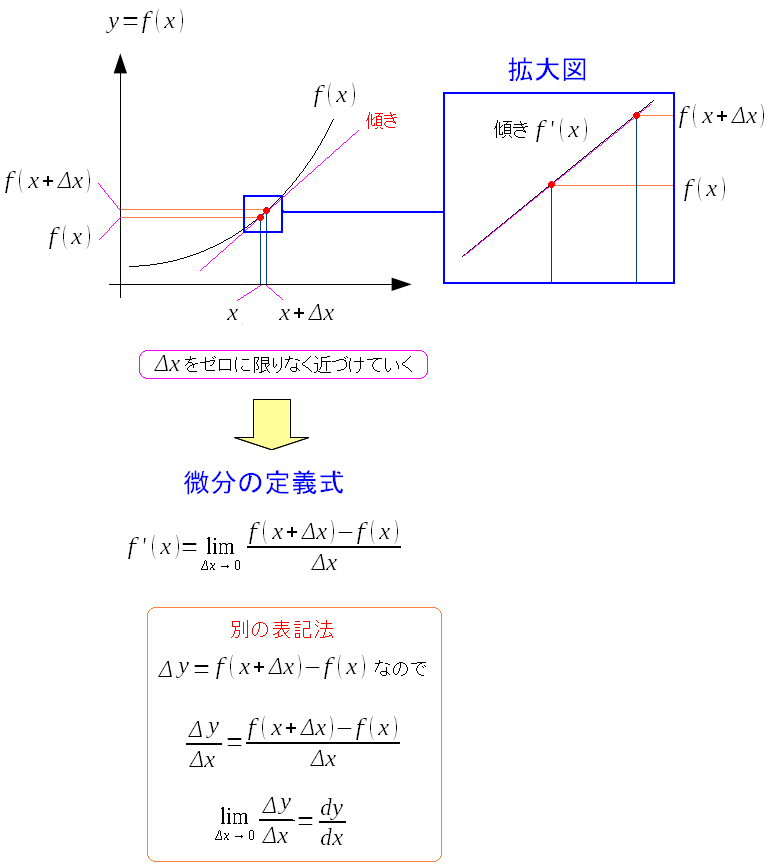
ここで1変数の関数の微分の定義式を書いてみる
| 微分の定義式 |
|---|
 |
|
1変数の関数の導関数を求める定義式だ。 関数の勾配(傾き、変化の割合)が求める事ができる。 |
線形化
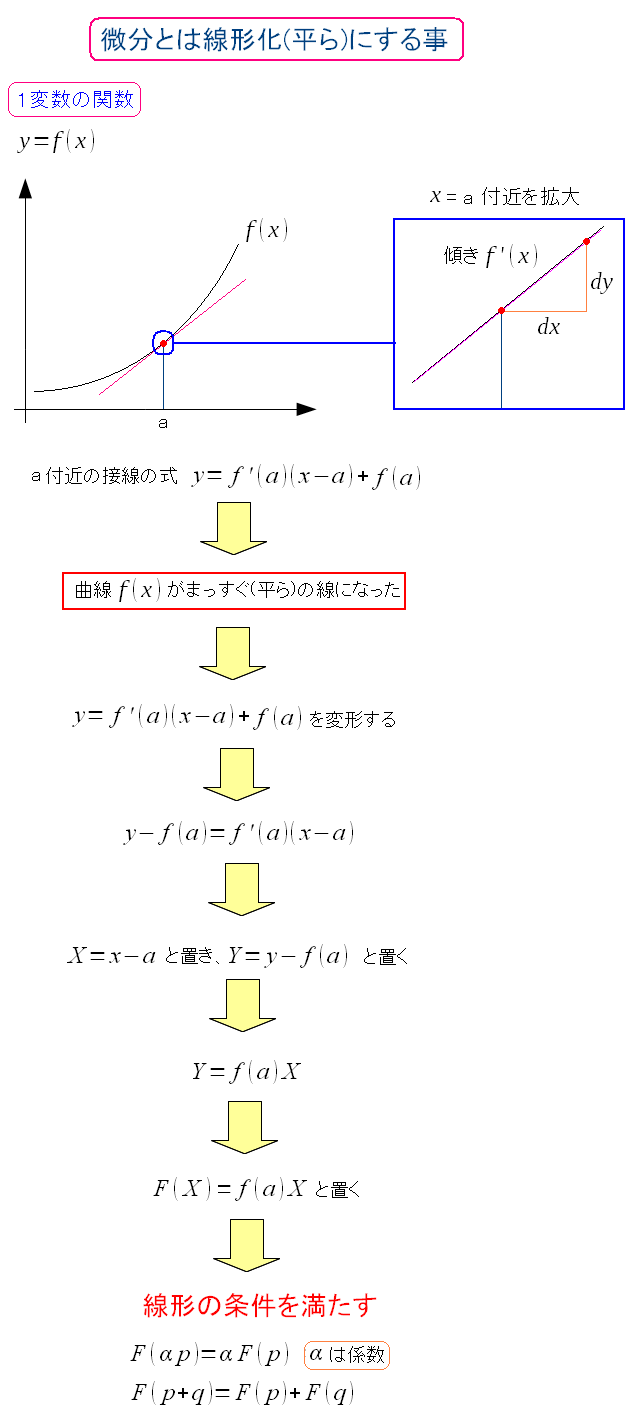
そして微分とは勾配や変化の割合を求める意味だけでなく 関数の線形化(平ら)という意味もある。
| 微分とは関数の線形化(平ら)にする事 |
|---|
 |
|
確かに微分とは1次元の曲線を、直線にしている。 すこし変形してXを変数とする「F(X)=F(a)X」の式にしてしまえば 点aでの接線の式は、線形の条件を満たす関数になっている。 |
いかにも微分には詳しいような書き方をしているのだが・・・ この原稿の編集中に線形化の話を知ったのら-!! それまでは線形の意味が、全くわかっていなかった。 つまり大学で 線形代数を学んだはずだが、理解してへんかった!! というのだ。 そのため以下の事も気づかなかった。
| 線形関数でない物 |
|---|
 |
|
「f(x)=x+1」という関数は線形関数ではない。 線形条件を満たさないからだ。 直線関数であっても、案外、線形関数になってない場合があるのだ。 |
偏微分
微分の話は、1変数の関数における変化の割合を求める事だった。 ここからは多変数の関数における変化の割合の話になる。 わかりやすく2変数の関数の話で説明する事にした。 例として、平面(板)の下からガスバーナーで板を熱した場合 平面の温度分布を使って説明する事にした。 強調しておくが 私が考えた説明方法 なのだ。 本やサイトの丸写しばかりではないのだ。と自慢してみる。
| 火を使って平面(板)を熱した時の平面(板)の温度分布 |
|---|
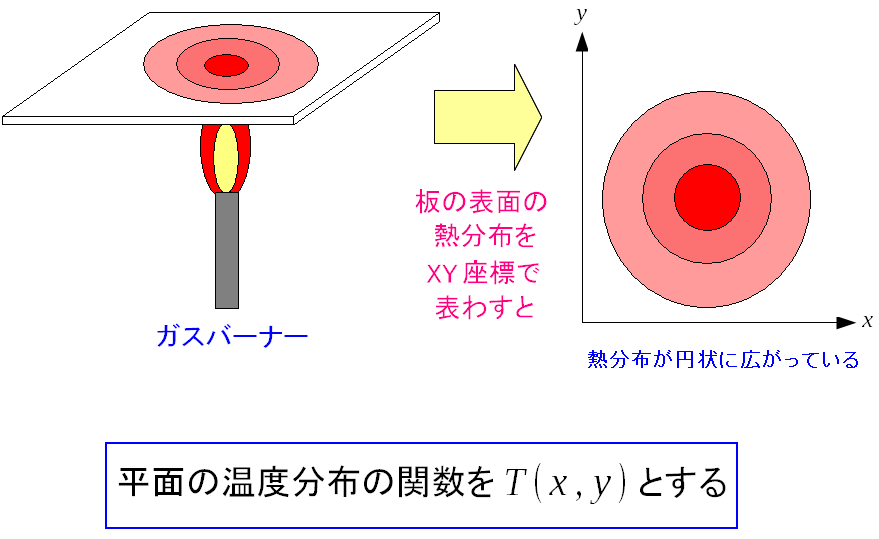 |
| 2変数(XY平面)の例として、これが一番かなぁと思ったりする。 |
ところで偏微分とは平たく言えば・・・
決まった方向の断面の傾きを見る
なのだ。
2変数の関数の場合、2つの方向(2通り)の偏微分があるのだ。
言葉で説明するよりも具体例を挙げた方がわかりやすい。
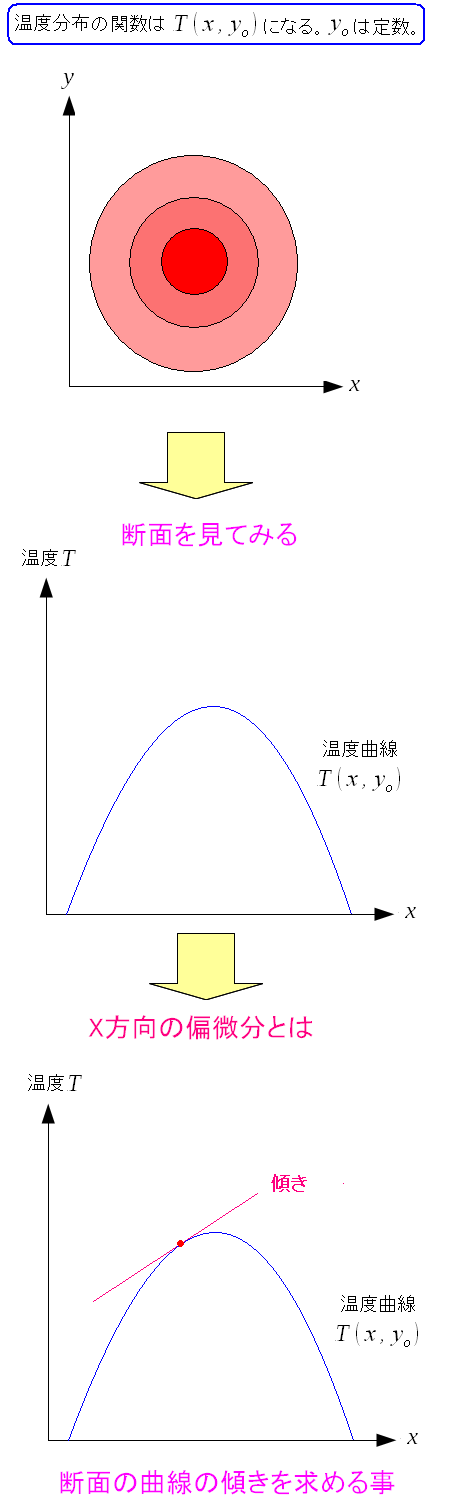
まずはX方向の偏微分。
| X方向の断面の温度分布を見てみる |
|---|
 |
|
変数Yの値を固定させる。 そして断面を見るのだ。 |
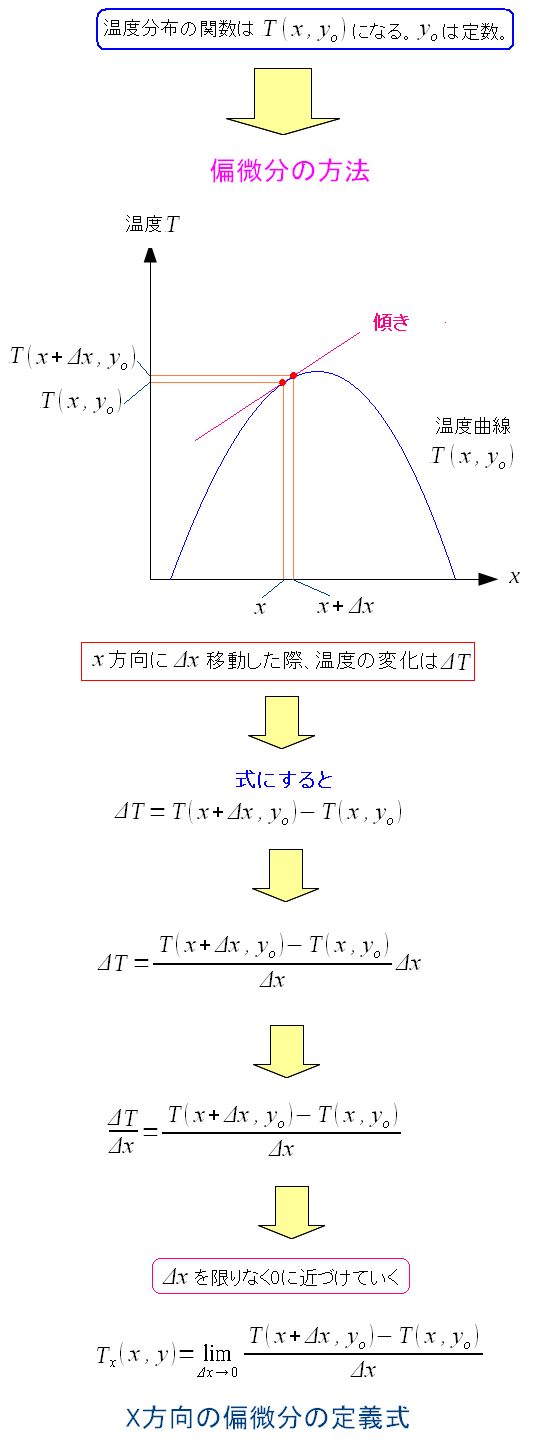
X方向の偏微分を式にすると以下のようになるのだ。
| X方向の偏微分の定義式 |
|---|
 |
|
Yの値を定数として見ているので、温度分布を表わす関数を Xの関数として考えれば良いのだ。 そして変数Xの1変数の関数として、微分すれば良いのだ。 |
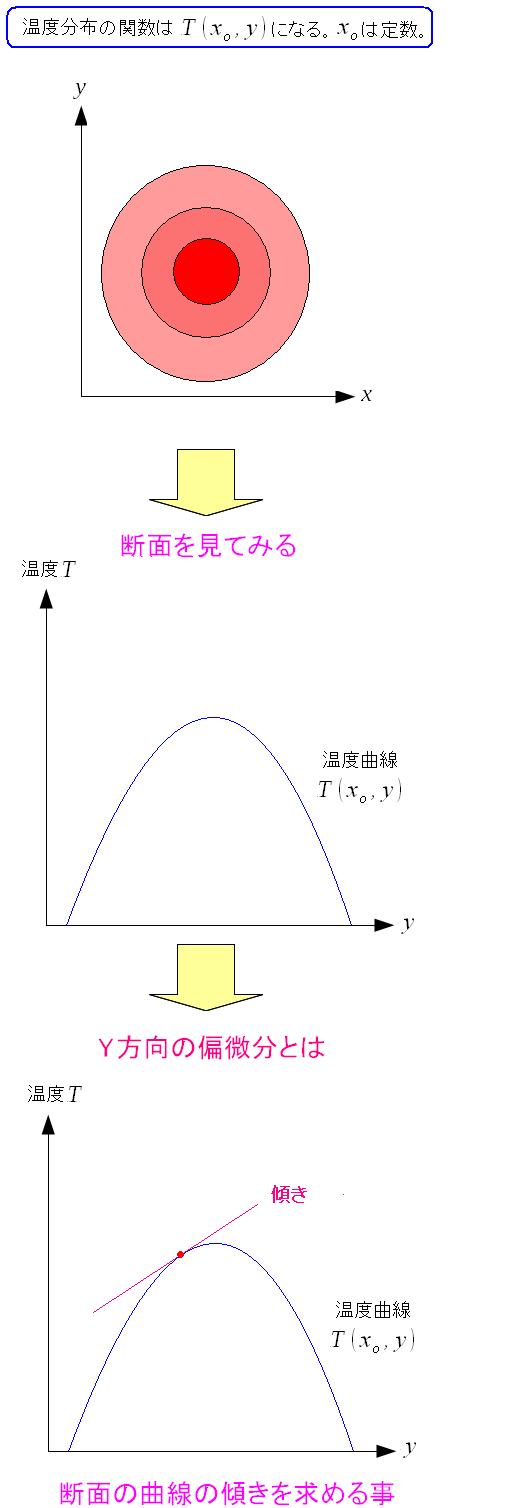
そしてY方向の偏微分を見る。
| Y方向の断面の温度分布を見てみる |
|---|
 |
|
変数Xの値を固定させる。 そして断面を見るのだ。 |
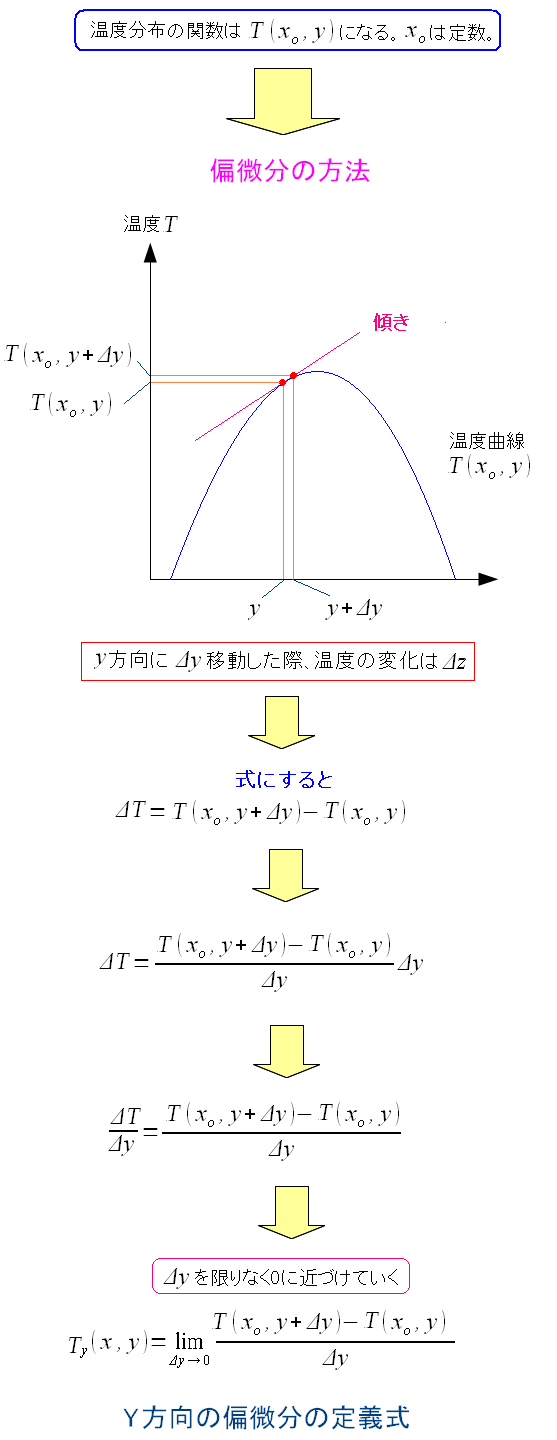
Y方向の偏微分を式にすると以下のようになるのだ。
| Y方向の偏微分の定義式 |
|---|
 |
|
Xの値を定数として見ているので、温度分布を表わす関数を Yの関数として考えれば良いのだ。 そして変数Yの1変数の関数として、微分すれば良いのだ。 |
2変数の関数の場合、2つの偏微分があった。 N個の変数の関数の場合は、N個の偏微分がある。 偏微分とは 特定の変数の方向の微分 というわけなのだ。
方向微分
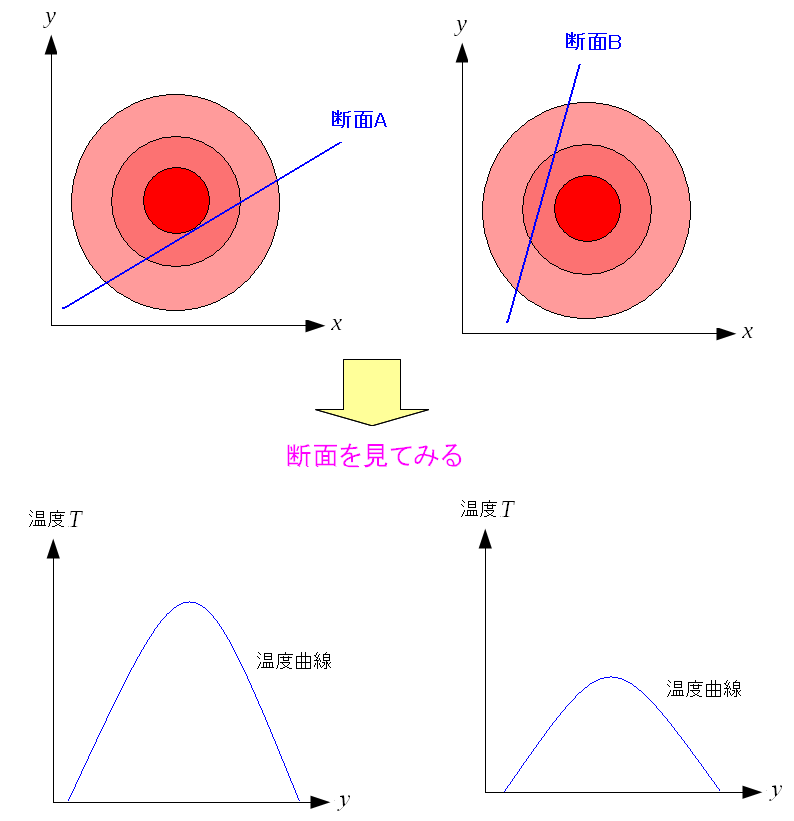
偏微分は1つの変数の関数と考え、他の変数は定数とみなし 1変数の微分として考えた。 そのため、微分の方向は決まってしまう。 好きな方向への微分はあらへんのか! と思いたくなる。 それを行なうのが・・・ 方向微分 なのだ。 ここでも板(平面)の温度分布で考えてみる。 方向微分とは、板(平面)の好きな方向の断面を見て 断面の傾きを見る事なのだ。
| 好きな方向の断面の変化量を見るのが方向微分 |
|---|
 |
|
方向によって温度曲線に違いがある。 方向別の温度の変化の割合を見たい時に、方向微分を使うのだ。 |
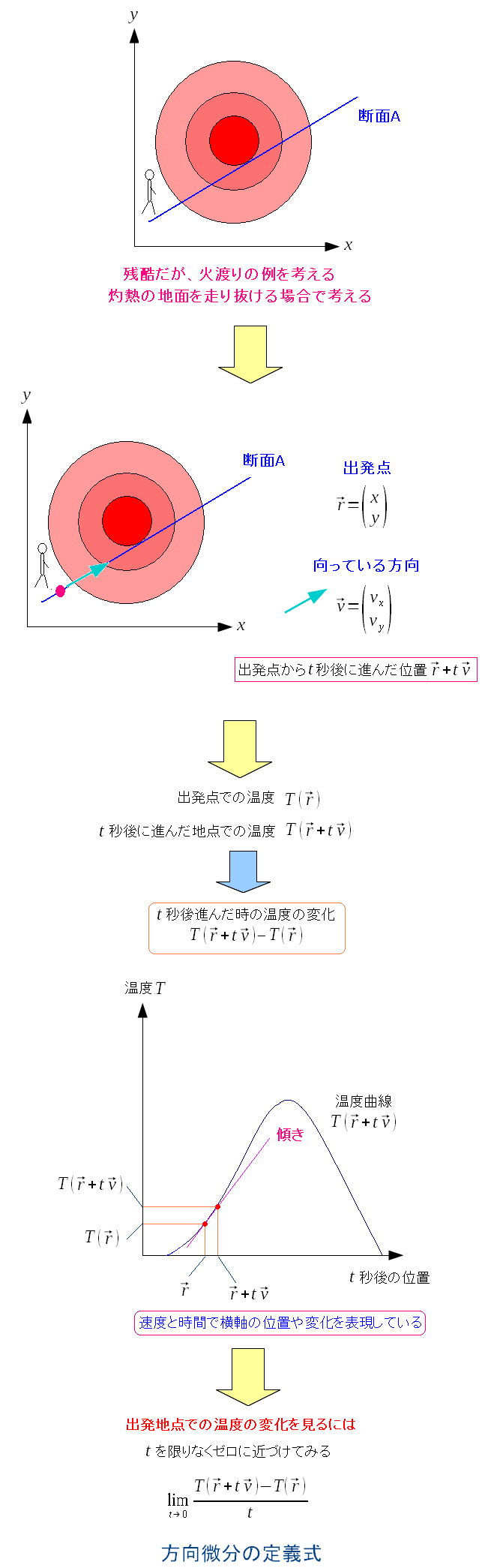
方向微分を求めるのだが、この時、必要になるのが 簡単な力学の知識 数学は抽象世界を描くため、一般化して説明する場合が多い。 だが、どう考えても、力学の概念を使って説明している事もある。 方向微分だと 速度ベクトル が出てくる上 変数tという仮面を被った時間 が出てくるのだ。
| 方向微分の定義 |
|---|
 |
|
残酷だが、火渡りする人を例にしてみた。 灼熱の地面を走り抜ける。その方向における温度の変化の割合を見るのが 方向微分になる。 どういう経緯かはわからないが、変化の方向に走る抜けるという発想のため 速度や時間の話が出てくる。そのため簡単な力学の知識が必要になる。 ただ、一般化するために、力学を隠蔽しようとする様子(?)が垣間見えるのだ |
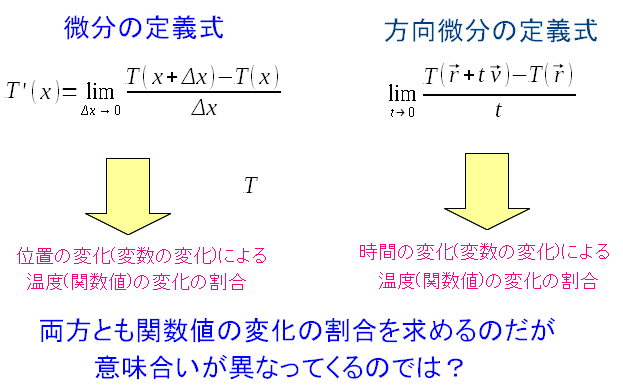
さて、方向微分の定義式が出てきた。ここでも注意が必要だ。 1変数の関数の微分と比較すると、違いが浮き彫りになる。
| 1変数の関数の微分と、方向微分との比較 |
|---|
 |
|
普通の微分の場合、変数Xの変化に伴う関数の変化の割合を求めている。 方向微分は、パラメーター(時間t)の変化に伴う関数の変化の割合を求めている。 同じ量の変化の割合を求める式なのか、違い物が出てくるのか 確かめてみる必要がある。 |
普通の微分(?)と、方向微分の違いを、簡単な方法で確かめてみる。 そこで以下の2変数の関数で比較してみる。
| 方向微分と微分の変化量を比較してみる |
|---|
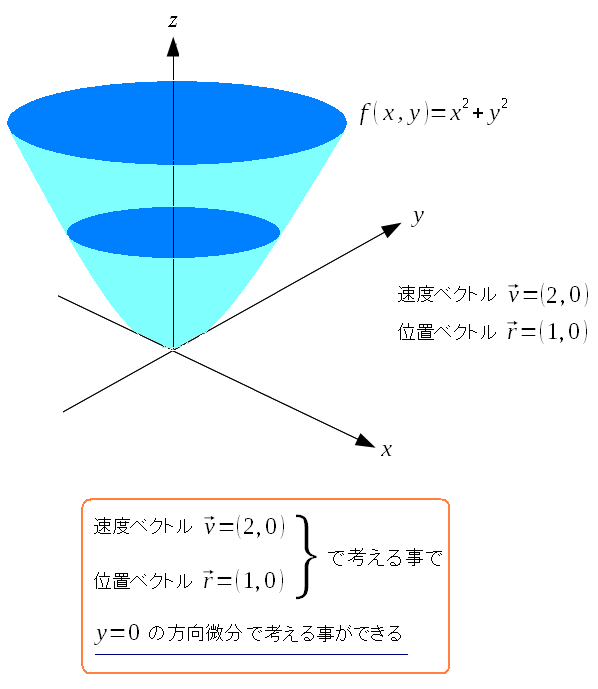 |
| 比較しやすくするため、y=0の時の断面の変化量で見てみる事にした。 |
まずは方向微分で変化量を見てみた。
| 方向微分で変化量を見てみた |
|---|
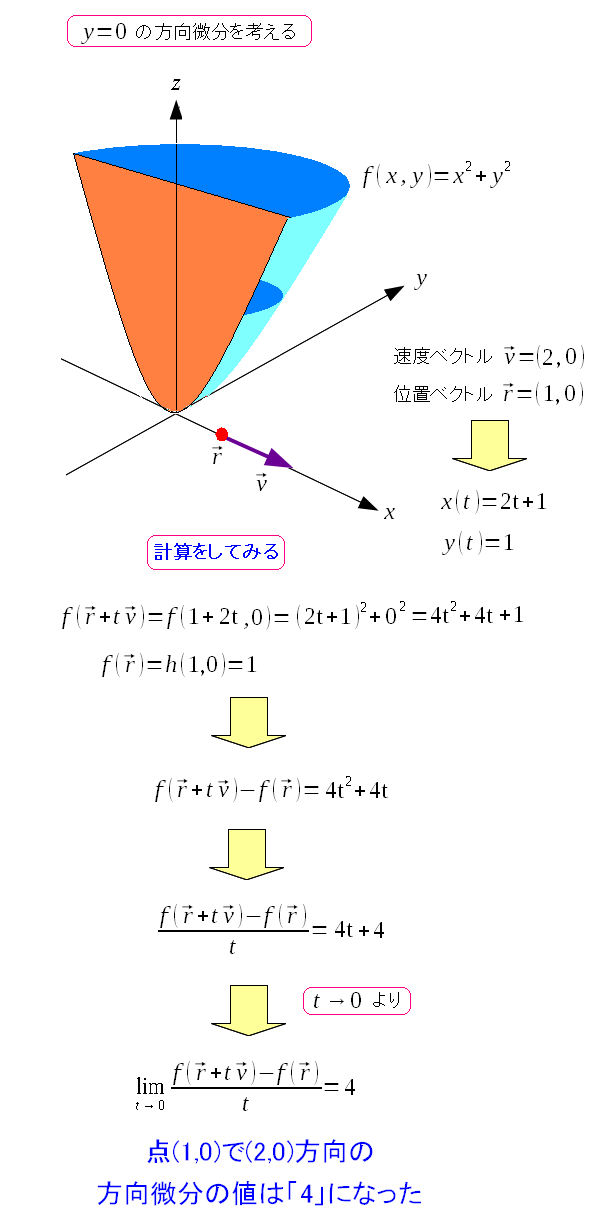 |
| 変化量は「4」と出た。 |
次に1変数の関数での変化量を見てみた。
| 1変数の関数での変化量を見てみた |
|---|
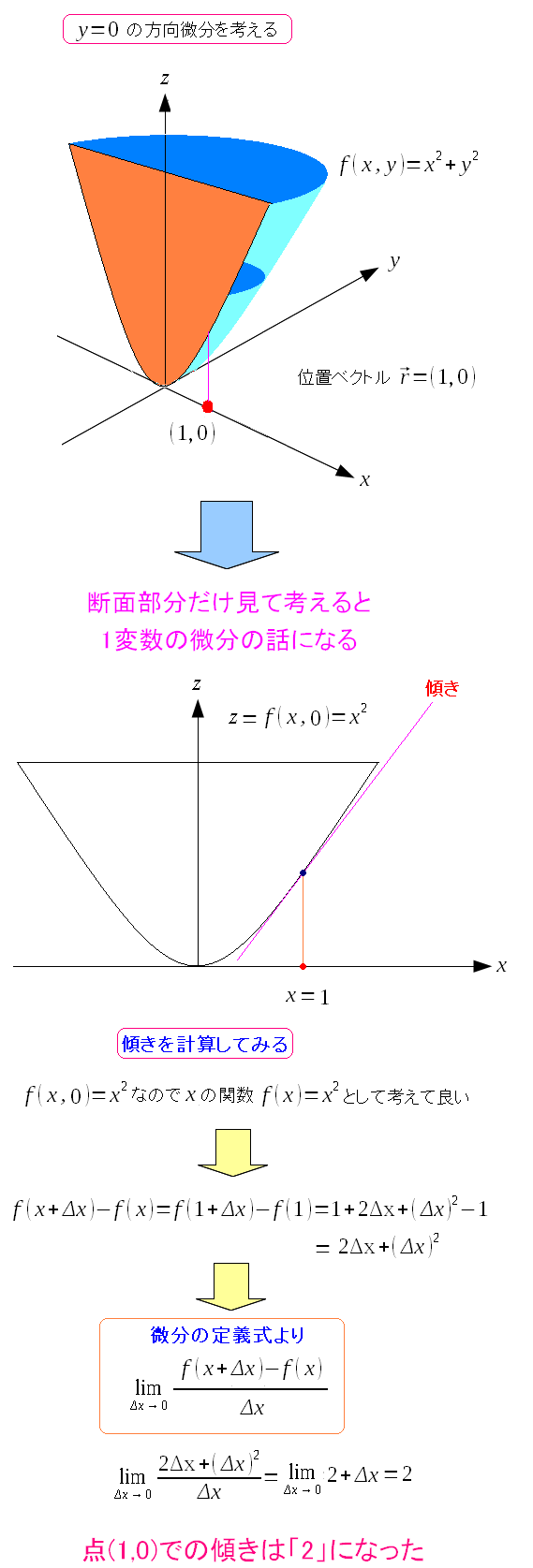 |
| 変化量は「2」と出た |
方向微分で求めた関数の変化の割合と 微分で求めた関数の変化の割合は異なる!! なのだ。 どの変数の変化に伴う関数値の変化の割合なのか、注意が必要だ。 方向微分の話には続きがあるのだが、テイラー展開と全微分を説明した後で 再度、方向微分の話をします。
テイラー展開
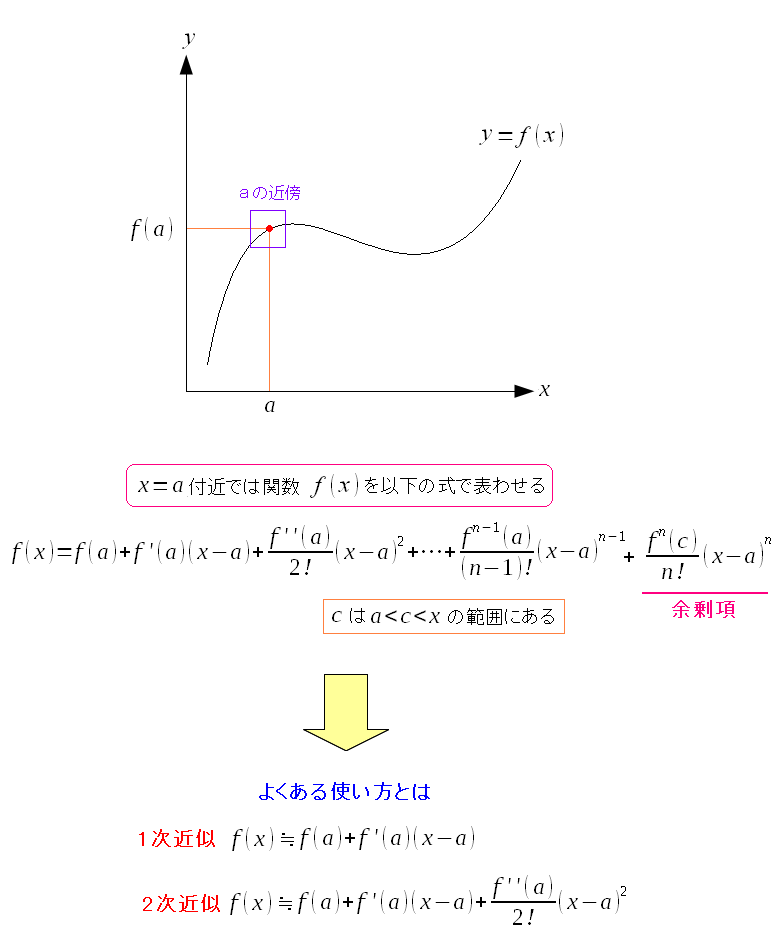
関数を多項式に近似するのがテイラー展開だ。
| テイラー展開とは関数を多項式で近似する事 |
|---|
 |
|
微分可能な関数であれば、x=a付近では上のような多項式の関数に近似できるのだ。 近似できるのは、aの周囲だが、多項式で近似できるので、広範囲に使われる。 |
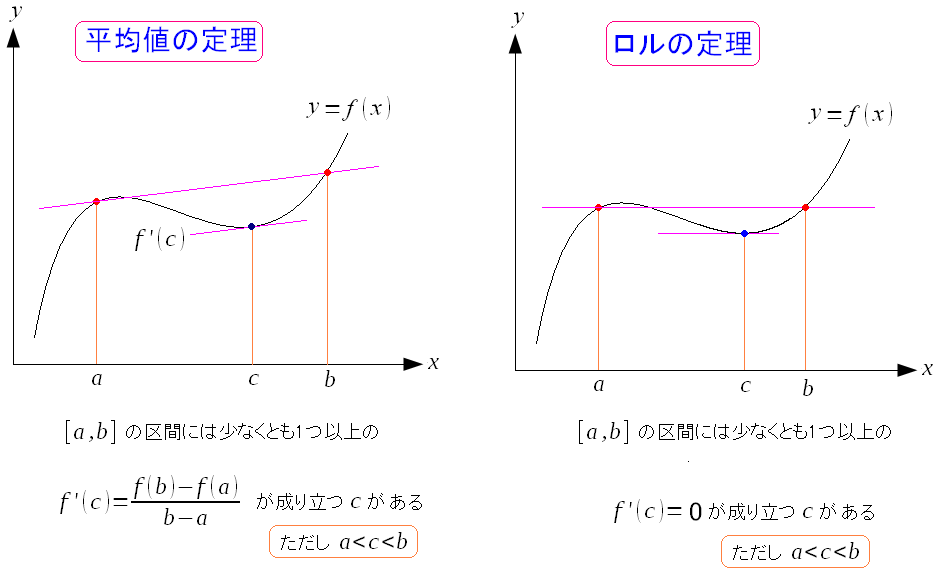
ふと思った。 どうやって、こんな式を導いているねん? 調べてみると、わかりやすい資料が見つかった。 微分積分学I (web補講)テイラー展開・テイラー級数(日本工業大学) 資料によれば・・・ 平均値の定理とロルの定理を使う というのだ。
| 平均値の定理とロルの定理 |
|---|
 |
|
平均値の定理とロルの定理だ。 ロルの定理は、平均値の定理の特殊な場合になるのだ。 |
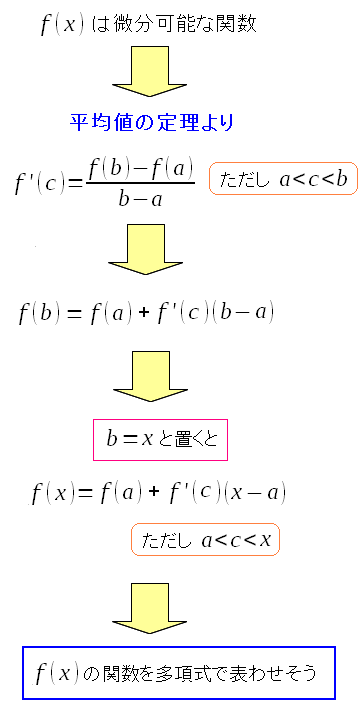
平均値の定理とロルの定理を使って、上手にテイラー展開を導くのだ。 まずは平均値の定理を使って、微分可能な関数を、別に形に置き換えてみる。
| 平均値の定理を使って、微分可能な関数を、別に形に置き換えてみる |
|---|
 |
|
平均値の定理を使えば、微分可能な任意の関数を 多項式で表現できそうな感じに思えてくる。 この時点では、余剰項が大きいため、x=aの近傍でも ごく狭い領域でしか近似ができない。 |
今度はロルの定理を使う。
| ロルの定理を使って、より関数を具体化していく |
|---|
 |
|
余剰項を、多項式の一部分に置き換えることができるため 多項式に置き換えたい関数の中身が具体的になってくる。 |
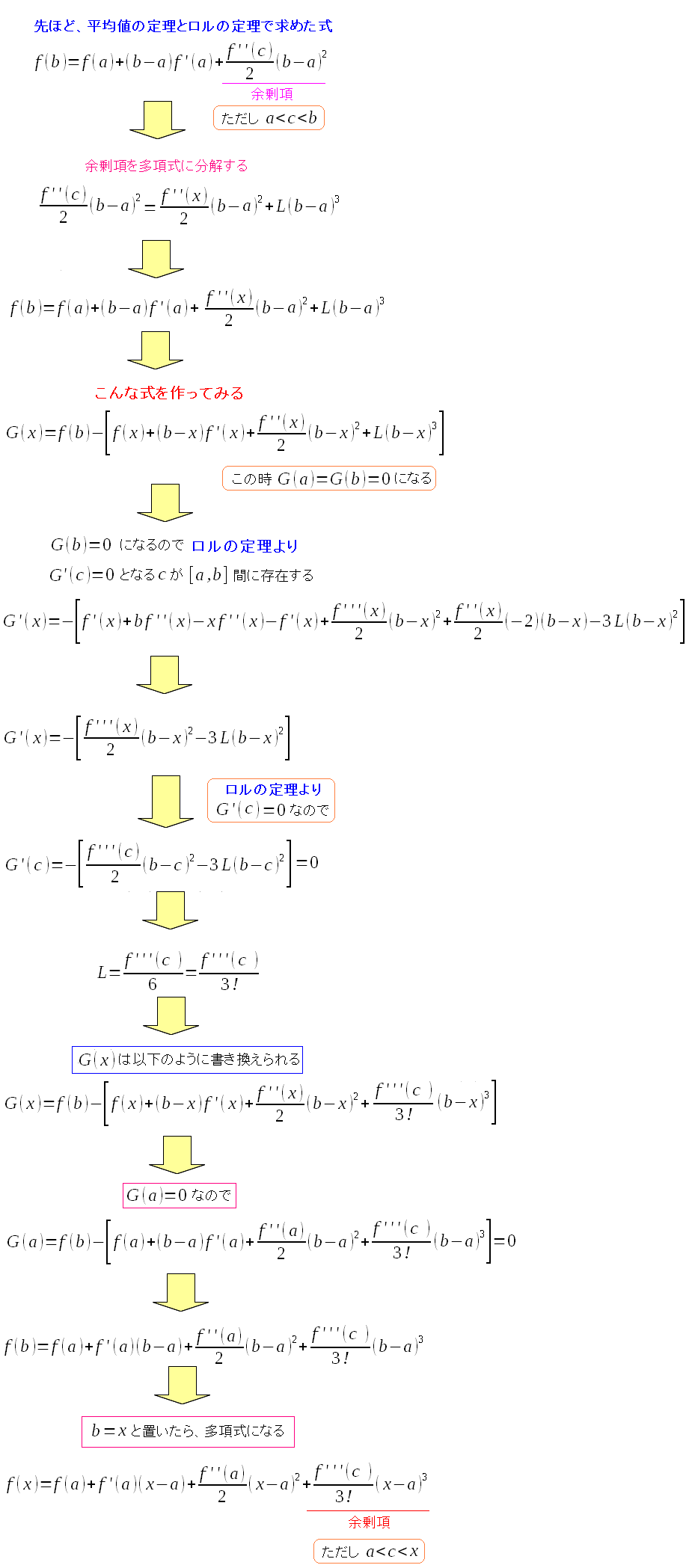
そして平均値の定理とロルの定理を使って、どんどん余剰項を多項式に変えていく
| 平均値の定理とロルの定理を使って余剰項を多項式に変えていく |
|---|
 |
|
テイラー展開の形になっていく。 ここから先も、平均値の定理と、ロルの定理を使っていけば 元の関数に近い、多項式の近似関数が求められる。 それによりx=aの近傍の範囲も広がっていくのだ。 |
目からウロコ なのだ
全微分
微分、偏微分、方向微分を説明した所で、全微分を説明するのだ。 といっても難しくはない。 考え方は、1変数の微分と同じなのだ。 全微分とは関数の傾き(勾配)を求める事 なのだ。 多変数の場合、偏微分や方向微分の場合があるので 偏微分や方向微分とを区別するため「全微分」と言っているようだ。 さて、そこで先ほど使った、熱した板(平面)の温度分布を例にして 全微分を説明していく。
| 板上の2点の温度差を考える |
|---|
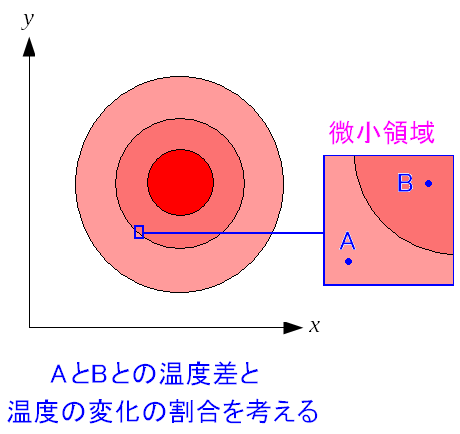 |
| 外側寄りの点Pと、内側寄りの点Qの温度差を考える。 |
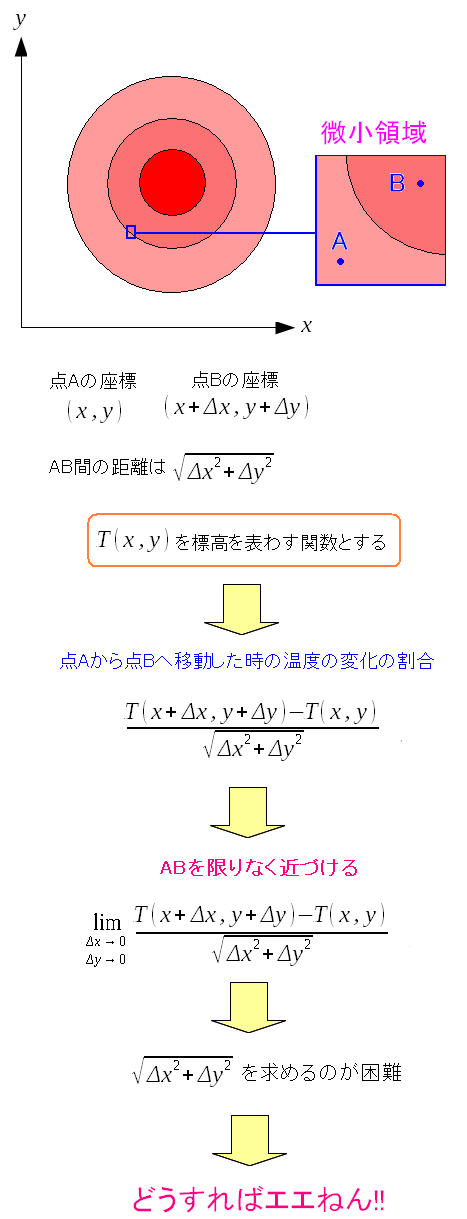
だが、2点間の距離を求めて、温度の変化の割合を 直接求めるのは、案外、困難なのだ。
| 直接、変化の割合を求めるのは困難 |
|---|
 |
|
1変数の微分と違い、いきなり直線距離を使って 関数の変化の割合を求めるのは困難なのだ。 |
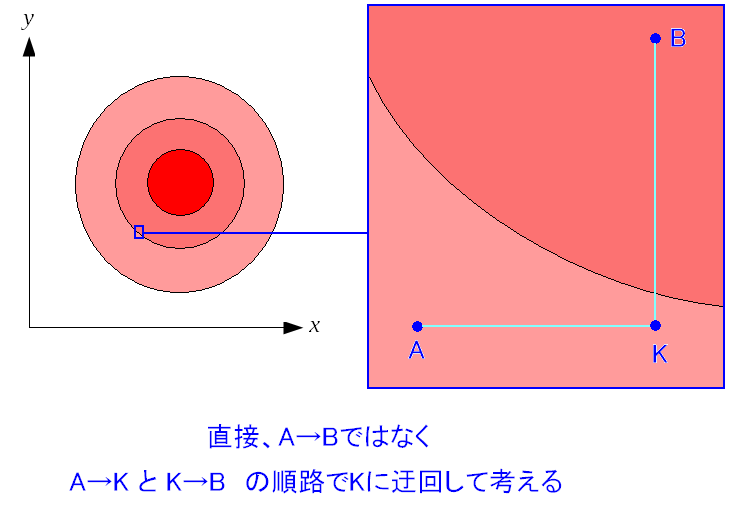
そのため迂回した道順を使うのだ。
| 迂回して考える |
|---|
 |
|
途中、点Kを設けて、Kに迂回した順路を考える。 「急がば回れ」ではないが、迂回して求めた方が遥かに楽なのだ。 |
早速、迂回して関数の値の変化量(温度変化)を求めてみる
| 迂回して関数の値の変化量を求めてみる |
|---|
 |
|
途中、点Kを設ける事で、A→Kの時の関数の値の変化量の近似値と K→Bの時の関数の値の変化量の近似値が求めやすくなる。 AB間の距離をゼロに近づける事で、点Aの地点での関数の変化量が求められるのだ。 ここで求まった式を「全微分」というのだ。 |
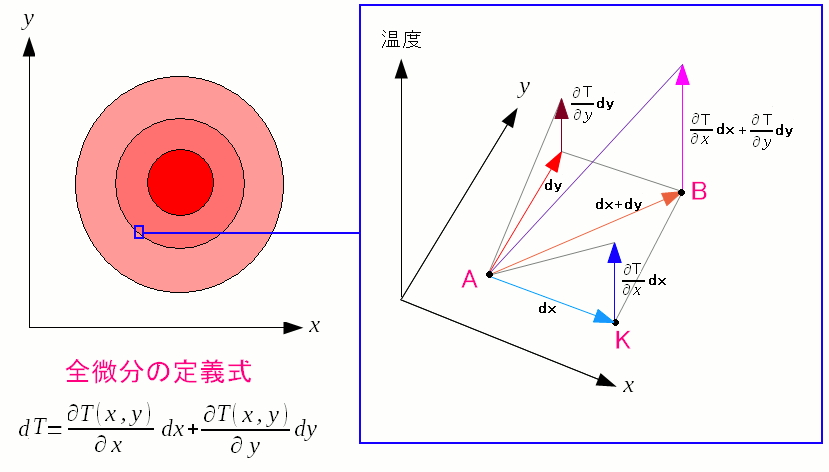
全微分の定義式を知る事ができた。 そして気づいた。 全微分は関数の値の変化量であって 変数の変化に対する、関数の変化の割合ではない!! いかに、学生時代、何も考えずに数学を勉強したのかがバレバレだ。 でも、20年も昔の話なので、気にしない。 全微分の式の意味を考えてみる。
| 全微分の式の意味 |
|---|
 |
|
2変数の関数の全微分の場合、関数の値の増加量は X方向の微小量の増加と、Y方向の微小な増加の和になっている。 視覚的にすると、わかりやすくなると思ったのだが・・・ |
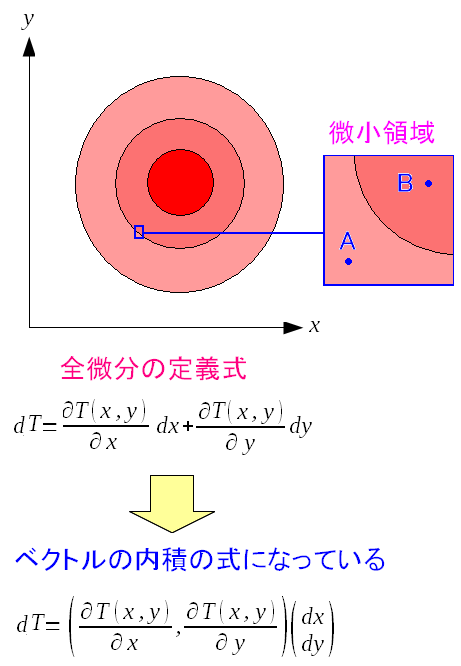
視覚的に表わしてみたのだが、これだと イマイチ、よくわからへん!! すなわち、全くわからないという事なのだ。 だが、ある事に気づく。 全微分は内積の式やん
| 全微分の式は2つのベクトルの内積 |
|---|
 |
|
全微分の式は、2つのベクトルの内積になっているのだ。 (dx,dy)のベクトルは、変数の変化の向き、即ち、移動の方向のベクトルなのだ。 |
学生時代、全微分が内積なのには、気づかなかった。
いかに数学を理解していなかった事がバレバレだ。
内積である事に気づいた後、次の事にも気づく。
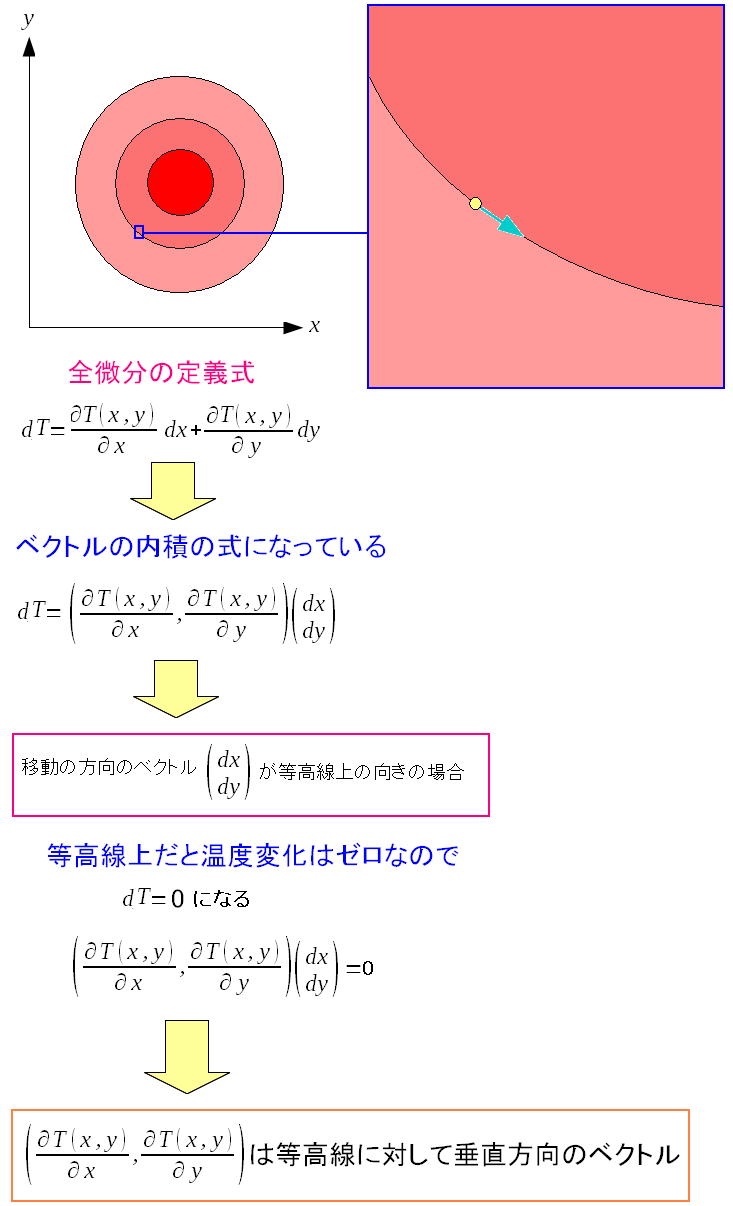
等高線上の移動の場合
なのだ。
| 全微分の式の意味(等高線上の移動で考える) |
|---|
 |
|
移動の向きのベクトル(dx,dy)が等高線上の方向だと 温度の変化はゼロのため、全微分の式はゼロになる。 すると自動的に、もう1つのベクトルが、等高線に対して垂直方向のベクトルになるのだ。 |
等高線に対して垂直方向のベクトル。
このベクトルの向きは
等高線の山の方なのか、谷の方なのか
が問題になる。
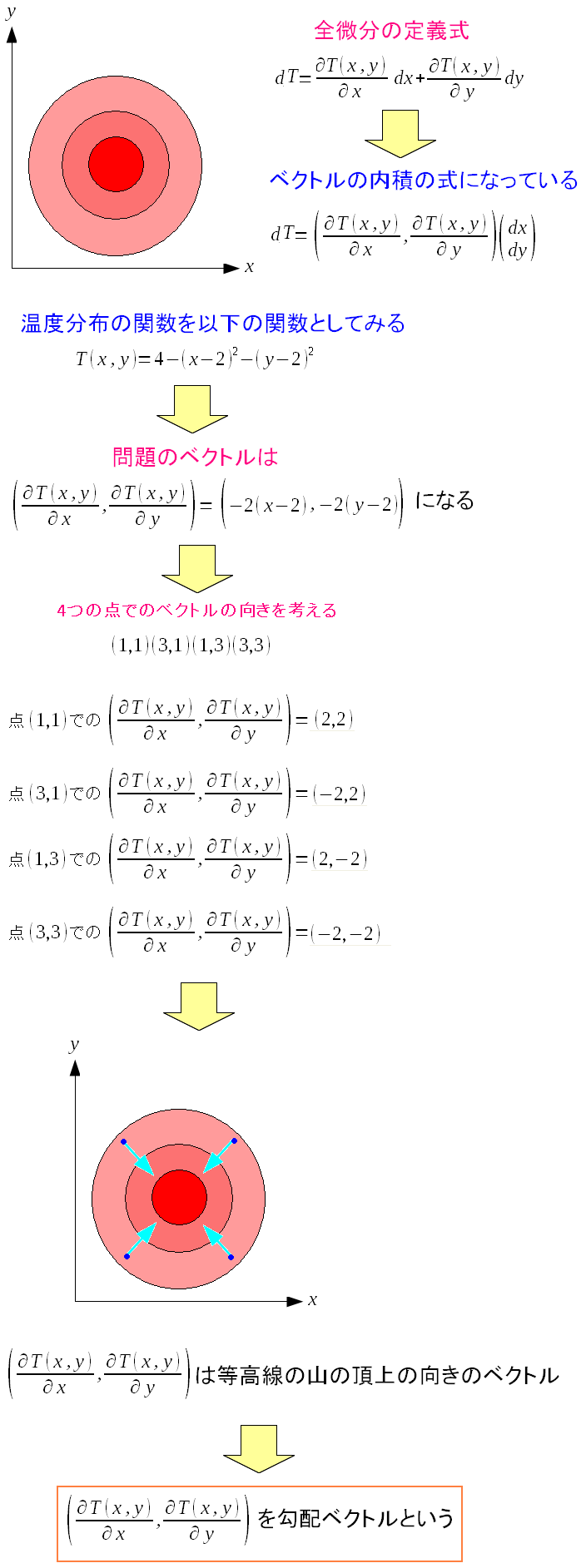
実際に、2変数の関数を使って、視覚的に見てみる事にした。
| 2変数の関数を使って、視覚的に見てみる |
|---|
 |
|
問題になっているベクトルは、高い所に向うベクトルになっている。 このベクトルを勾配ベクトルというのだ。 |
単純な物なら手計算でできるのだが、少し複雑になると、面倒になるし
もっと複雑になると、手計算では無理だし、図も描けなくなる。
もっとわかりやすい方法がある。
数学ソフトの
GeoGebraを使うのだ!!
GeoGebraの賢いのは、関数の微分や偏微分を出してくれるのだ。
そのため関数を入力すれば、簡単に勾配ベクトルを求められる。
以下の資料を参考にしたのだ。
ベクトル解析における3次元動的数学ソフトウェアの教育利用と検証
現在、日本大学の濱田龍義さんの資料で、私にGeoGebraを紹介してくださったのも濱田さんなのだ。
福岡のOSCでもお世話になった方なのだ。
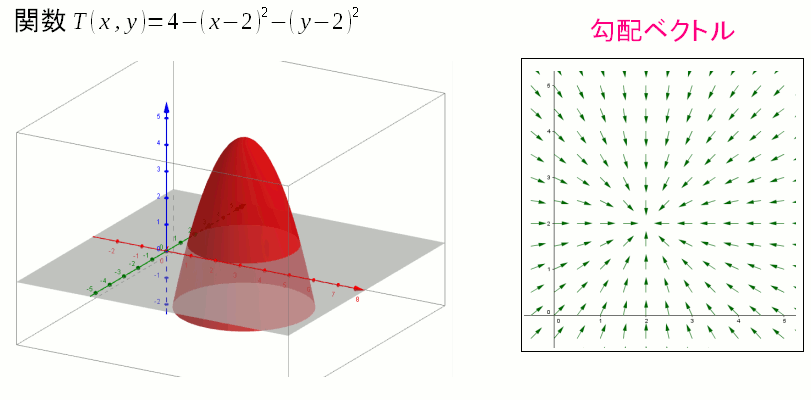
| 2変数の関数と勾配ベクトル |
|---|
 |
|
GeoGebraを使うと、手軽でわかりやすい ベクトルの大きさは、同じ長さにそろえましたが 勾配の度合いを見るために、ベクトルの大きさを、長さで表現する事もできる。 |
GeoGebraを使って、少し遊んでみる。 2つの山の場合の勾配ベクトルがどうなっているのか見てみる。
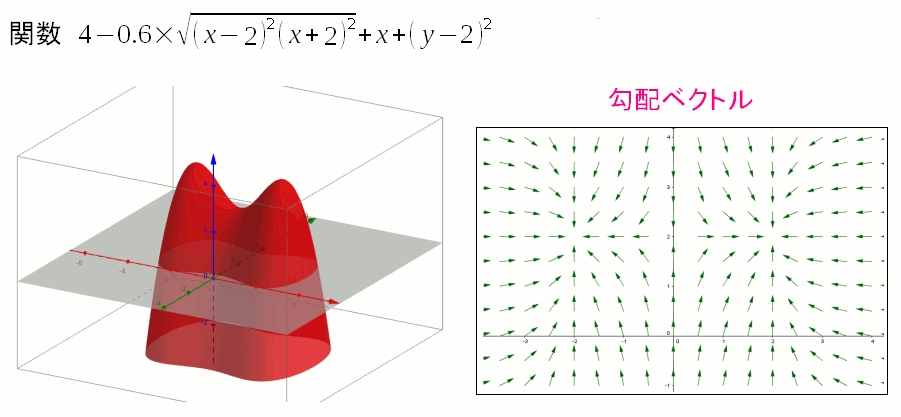
| 2つの山がある場合の勾配ベクトルを見る |
|---|
 |
|
x=0のところでは、y=0の部分が高い山なので、y=0になる方向に向いている。 だが、x=0からずれると、片方の山に向った方向になる。 |
GeoGebraは数学や物理を視覚的に学ぶのに非常に便利なソフトなのだ。
方向微分の意味
方向微分の話が中途半端になっていたので、続きを書く事にする。 方向微分が具体的にどういう量なのか計算してみた。
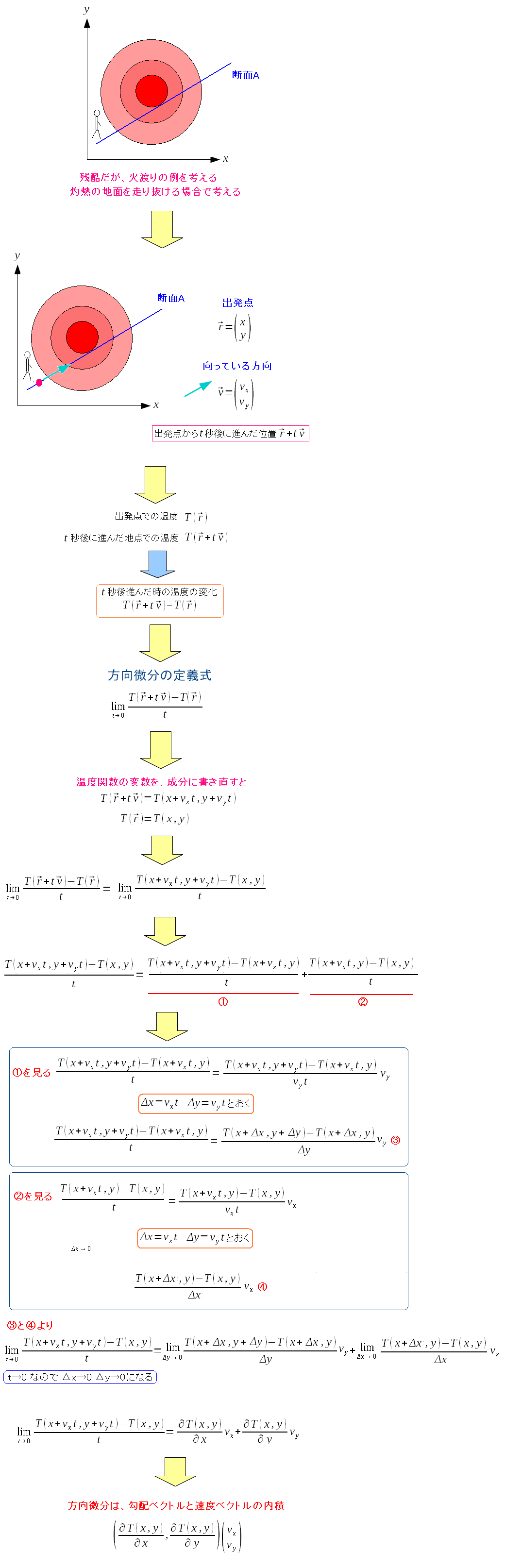
| 方向微分が具体的にどういう量なのか計算してみた |
|---|
 |
|
方向微分は、勾配ベクトルと速度ベクトルの内積なのがわかった。 ただ、方向微分が、速度vで移動する時、時間(t)の変化における 関数値の変化の割合としか言えない。 |
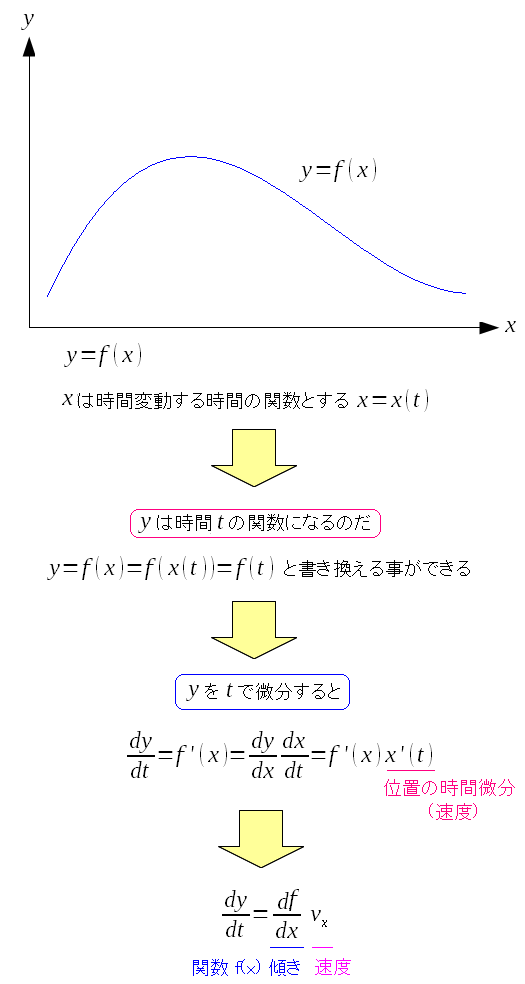
ところで・・・ 方向微分をどう解釈すればエエのか、わからへん!! なのだ。 方向微分は、使い道があるのかいなと思ってしまう。 だが、意外な事を知る。 合成関数の微分は方向微分 なのだ。
| 合成関数の微分は方向微分 |
|---|
 |
|
1変数の関数で確かめてみると、関数の傾き(勾配)と速度の積になっている。 こんな話、全く知らなかった。 |
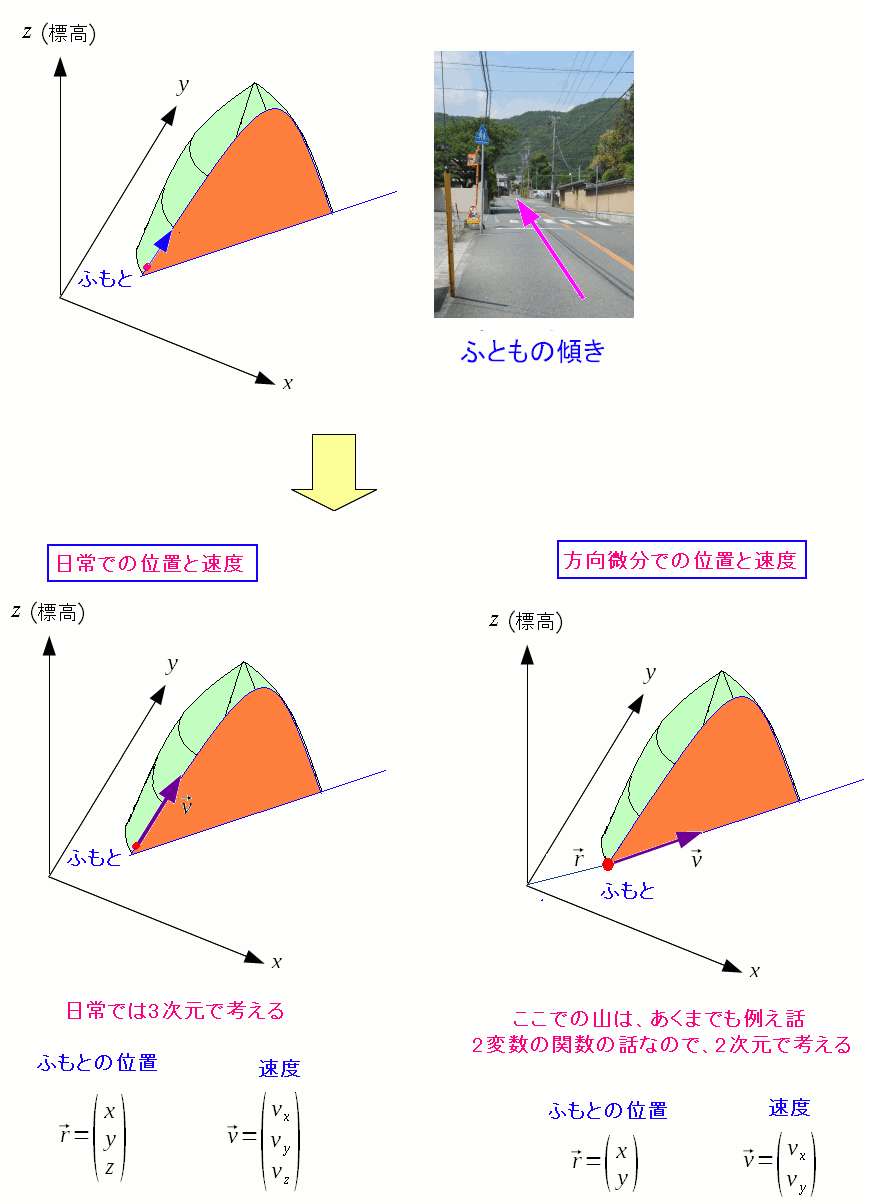
数学を勉強していない事がバレバレなのだ。 ただ、方向微分の意味がわかったわけではない。 でも、使い道がないわけではない。 単に私が知らないだけ なのだ。 ここで方向微分の話を出したのは理由がある。 あとで出てくる多様体の話と結びつくからだ。 あと2変数の関数の全微分なのだが、山を使って説明しようと考えた。 だが、山を使って説明した場合・・・ 2次元と3次元を混同してしまう! の問題が起こってしまう。 私自身、そのワナに嵌まってしまったので、折角、作った絵を ボツにせざる得なかったのだ。
| 山を使った説明が良くない理由 |
|---|
 |
|
山で考えると、日常の山登りを考えてしまう。 そのため速度ベクトルといえば、山の斜面に向いた方向を考える。 無意識のうちに、3次元で考えてしまうのだ。 だが扱うのは、2変数の関数なので、あくまでも2次元の世界だ。 そのため、日常の感覚とズレてしまい、混乱や誤解を招いてしまうのだ。 |
以上、私の失敗談を書いたのだ。
電磁気学入門の目次
| 電磁気学入門:目次 | |
|---|---|
| スカラーとベクトル | 簡単なスカラーとベクトルの話です。 ベクトルは方向と大きさを持つ量。方向という量持っているだけに注意が必要です。 |
| 静電気の発見からクーロンの法則 | 今でこそ当たり前の静電気や導体、絶縁体、電荷など どういう経緯で発見し、クーロンの法則まで至ったのかの話です。 |
| クーロン力、電場、近接作用 | 4つの力のうち、クーロン力の位置づけ 電荷が作り出す作用の電場。近接作用の話です。 |
| 微分、全微分、方向微分 | 簡単な微分、全微分、方向微分の話です。 ここをしっかり押さえないと、電磁気の数式の意味が わからなくなります。 |
| ベクトル解析 |
電磁気に必要なベクトル解析の話です。 勾配(grad)、2次元のグリーン定理 ストークスの定理の話です。 |
| 電位ポテンシャル | 電位ポテンシャルです。勾配と電場の関係を使って説明しています。 |
| 電気双極子 |
電気双極子の話です。 物質中で起こる分極を理解するのに必要です。 |
| ガウスの法則 | ガウスの法則の積分形、微分形の話です。 |
| ポアソンの方程式、ラプラス方程式 |
ポアソンの方程式、ラプラス方程式の話です。 単に電荷分布から電位を求めるだけの話にとどまらない 奥が深い分野です。ポテンシャル論、デルタ関数 グリーン関数、固有値問題について触れています。 |
| 静電場と渦なしの法則 |
静電場で、電荷を1周させた時の仕事はゼロ 微分形と微分形の渦なしの法則の話です。 |
| ビオサバールの法則 |
電気と磁場の関係の発見の話から ビオ・サバールの法則が導かれるまでの話です。 |
| 磁気双極子 |
磁気双極子の話で、回転電流になります。 物質中の磁場の話にも関連します。 |
| アンペールの法則 |
アンペールの法則の話です。 積分形・微分形だけでなく、閉回路に流れる電流が作る 磁気双極子の話なども書いています。 |
| ローレンツ力 |
磁場中を移動する電荷にかかる力(ローレンツ力)の話です。 ローレンツ力は相対性理論が絡んでいる事も紹介しています。 |
| ファラデーの誘導起電力の法則 | ファラデーの誘導起電力の話です。 |
| うず電流を使った簡単な物理実験 | 電力計に使われるアラゴの円盤。 そしてIH調理器で熱するために発生させる、うず電流は レンツの法則から電流が発生する原理を応用した物だ。 アラゴの円盤の実験と、IH調理器を使った実験です。 気分転換で読んでください。 |
| ベクトルポテンシャル |
わかりにくいベクトルポテンシャルの話です。 電位は電荷が作る電気のポテンシャルだが ベクトルポテンシャルは電流が作る磁場のポテンシャルの話です。 |
| オームの法則の微分形 | 微小領域でのオームの法則の話です。 |
| マックスウェルの方程式 |
4つのマックスウェルの方程式を書いています。 電場と磁場の変化を図にする事で rotの回転の意味も理解できます。 |
| ゲージ変換 |
ゲージ(gauge)は物差しの意味です。 マックスウェルの方程式をE(電場)とB(磁場)の関係式から φ(電位ポテンシャル)とA(ベクトルポテンシャル)の関係式に 書き換える際、ゲージ変換が使われます。 ゲージ変換の役目を書きました。 |
| 電磁波 |
マックスウェルの方程式から電波が伝わる様子を 視覚的に見てみる話です。 |
| 回転のrotはベクトルの微分 |
ベクトル解析や渦なしの法則で出てくるrotは ベクトルの微分という話です。 |
| 電磁気学の単位系 | 電磁気学の単位系の話です。 物理量の単位系の指数を見る次元解析 電磁気学の歴史と単位系の変遷について触れました。 |
| 電気泥棒:電気と法律の話 |
電気は物体なのか、無形物なのか。 明治時代に、電気を無断で使った場合、物か、そうでないかで 窃盗罪になるかどうかが裁判で問われました。 ちょっとした科学と法律の話です。気分転換で読んでください。 |
| 数ベクトルと基底ベクトル | ベクトルの話です。 矢印だけがベクトルでない事。 数ベクトルと基底ベクトルの違いの話です。 多様体、反変・共変ベクトルを理解するのに必要です |
| 多様体 | 空間を一般化した話です。 ▽(ナブラ)の正体に迫まります |
| 外積代数 |
外積、テンソルについて書いています。 極性ベクトル、軸性ベクトル 外積は行列で、ベクトルは見せかけの姿だった話です。 |
| ベクトルの双対関係 |
反変ベクトル、共変ベクトル、双対関係 ベクトル解析、外積代数の話 外積、テンソルについて書いています。 |
| ローレンツ力と相対性理論 |
磁場は電場の相対論的効果だった話です。 ローレンツ力を使って、導線が作る磁場を使って説明です。 |
| 微分形式 |
多様体の話の続きです。 座標に依存しない形での関数やベクトルの微分の話です。 ガウスの法則、アンペールの法則、マックスウェルの方程式が 鮮やかな形で表現できます。 ∇(ナブラ)の正体もわかります。 |
| 物理と対称性 |
マックスウェルの方程式をよく見ると対称性があります。 物理の方程式と対称性を数学的な観点でみると 意外なつながりがあるという話です。 |
| マックスウェルの応力 |
電気力線を弾性体(ゴム)とみなして、力の伝わり方などを 説明した考え方です。 |
| 電場エネルギー | 電場が持つエネルギーの式を導いた話です。 |
| 磁場エネルギー |
磁場が持つエネルギーの式です。 手抜きの説明と、直流RL回路を使った説明を書きました。 |
| ポインティングベクトル |
電磁エネルギーの流れ「ポインティングベクトル」の話です。 電磁波でもエネルギー保存則が成り立つ話から ポインティングベクトルを導いています。 |
| 電気エネルギーは導線の外を伝わる |
導線の外を電気エネルギーが流れる話です。 私が誤解した事、その誤解を解いていく過程を紹介しながら 「目からウロコ」にたどり着いた話です。 |
| 物質中の電場 | 物質中の電場の話です。 分極の話をしながら、物質中の電場の話をします |
| 物質中の磁場 | 磁性の話をしながら、物質中の磁場の話をします |
| 物質中のマックスウェルの方程式 | 物質中でもマックスウェルの方程式が成り立つ話です。 |
| 導体に侵入する電磁波 |
導体に侵入する電磁波が減衰していく話です。 表皮効果と同じ「表皮の厚さ」が出てきます |
| 表皮効果 |
目的の表皮効果の話です。 マックスウェルの方程式を解きながら 交流電流の周波数を上げると、表面にしか電流が流れなくなる話です。 |