上に書いている事には全く気づかなかった。
ただ、当たり前のように丸暗記しただけだった。
システム奮闘記:その105
(2016年5月22日に掲載)
静電気の発見からクーロンの法則
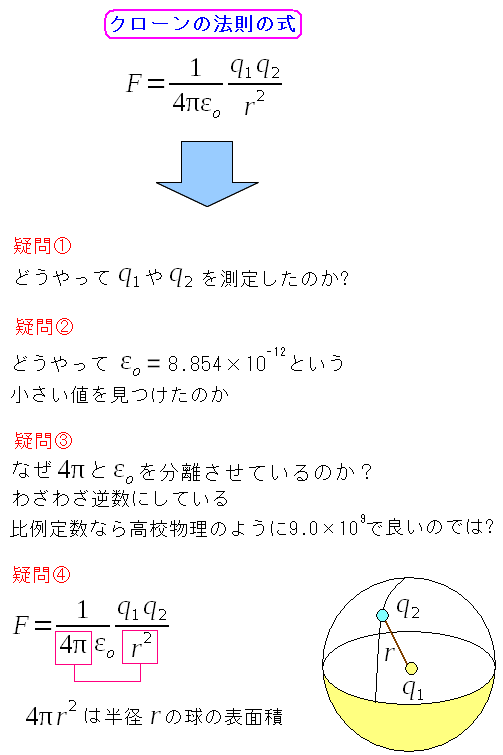
最初に正直な事を書くと、静電気の発見の歴史を無視して クーロンの法則だけ書いて、話を進めていた。 だが、色々な資料などを読んでいると 私が気づかへんかった事がある! となった。 考えれみれば、なんで、クーロンの法則が見つけられたのか 不思議になってしまった上、以下の疑問も出てきた。
| クーロンの法則の式についての疑問 |
|---|
 |
|
学生時代の時も、これを編集し始めた時も 上に書いている事には全く気づかなかった。 ただ、当たり前のように丸暗記しただけだった。 |
そして当たり前の事に気づいた。 私には物理の才能は全くあらへん!! 多少でも物理の才能があれば、今頃、技術者になっていたと思う。 事務系でも才能があるのかと言われると、答えに窮する。 弁護士のように法律に詳しいわけでもないし、 会計士や税理士のように会計や税務に詳しいわけでもないし、 社労士のように労務に詳しいわけでもない。 どっちも、冴えないのが本当の所なのだ・・・。 という事で、電気の歴史を調べる事になった。 そんなん、読む必要あらへん! と思う方は、飛ばして読んでください。 廃棄物を化学する(31)廃棄物とエネルギー2 (PDF) ウィリアム・ギルバート (物理学者)(Wikipedia) 『磁石論』の400年(京都大学) 静電気がはじめて発見されたのは?【静電気おもしろ教室】 真空について(金沢大学) 静電気で遊ぼう 静電気の工作・実験日本宇宙少年団(PDF) 静電気といえば、小学校の時に、よくやった遊びで、下敷きを擦って 頭に当てると、髪の毛が逆立つという実験だ。
| 下敷きを擦って頭に当てると、髪の毛が逆立つという実験 |
|---|
 |
|
小学校の時、よくやった遊びなのだ 今でこそ、小学生でも摩擦によって静電気が起こるのを知っているので、 静電気が起こす現象だとわかる。 |
静電気を帯びた物体が、物を引き寄せる力。 その歴史を見てみる。 古代、琥珀は宝石だったが、すぐに埃がついたりして汚れた。 タレスが、琥珀を擦る事によって、静電気という物が発生し それが物を引き寄せる力になると考えた。
| 琥珀が物を引き寄せる現象 |
|---|
 |
|
タレスが摩擦によって琥珀が物を引き寄せる力が発生する事を発見した。 でも、ここで疑問になったのは、当時、宝石だった琥珀なので 汚れていたら、皮か何かで拭くはず。なので、タレス以外でも 他の発見者がいても不思議ではない。 ただ、当時の一般庶民は琥珀が高価で手が届かなかったため 琥珀を触る人自体が少数だったと考えられる。 そして綺麗に琥珀を磨いた後、わざわざ紙や物に近づけて 引き寄せてみようとする発想がなかったかもしれない。 |
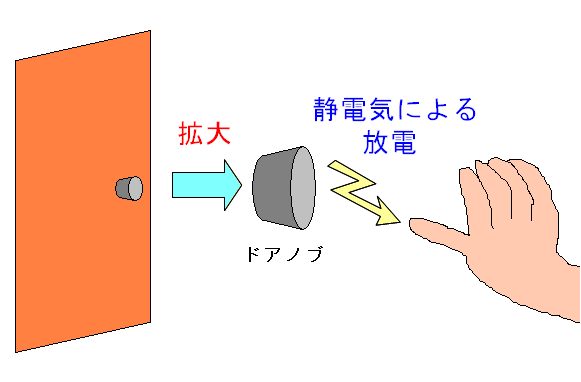
それから年月が経ち、1600年、イギリスの医者であり 物理学者だったウィリアム・ギルバートが、琥珀以外でも 摩擦による静電気の発生の有無を調べて 電気を帯びる物質と、そうでない物質を区別した。 この時「電気」という言葉はなかったのだが ギリシャ語で琥珀の意味の「elektron」があったため 静電気の力の事を「electric force」を呼んだのだ。 今まで・・・ 電気のエレクトロの語源は「琥珀」 だったとは知らへんかった!! ちなみに電磁気の教科書を見ると、その事が書いてあったので 全然、興味がなかったのが丸わかり なのだ。 ところでウィリアム・ギルバートは 電気と磁気は別物 と考えた。 そのため電気と磁場は別々に研究されていった。 電気と磁場の関連性に気づくには200年後の1800年代なのだ。 ドイツのゲーリケが1640年に静電気による放電を確認したのだ。 ドアのノブで静電気が走り、痛いと感じる現象なのだ。
| よくある静電気による放電 |
|---|
 |
|
ドアノブでの静電気の経験や、セーターを脱いだ時に パチパチときた経験があると思う。 パチパチの正体は放電現象で、数万ボルトの電気が流れているのだ。 |
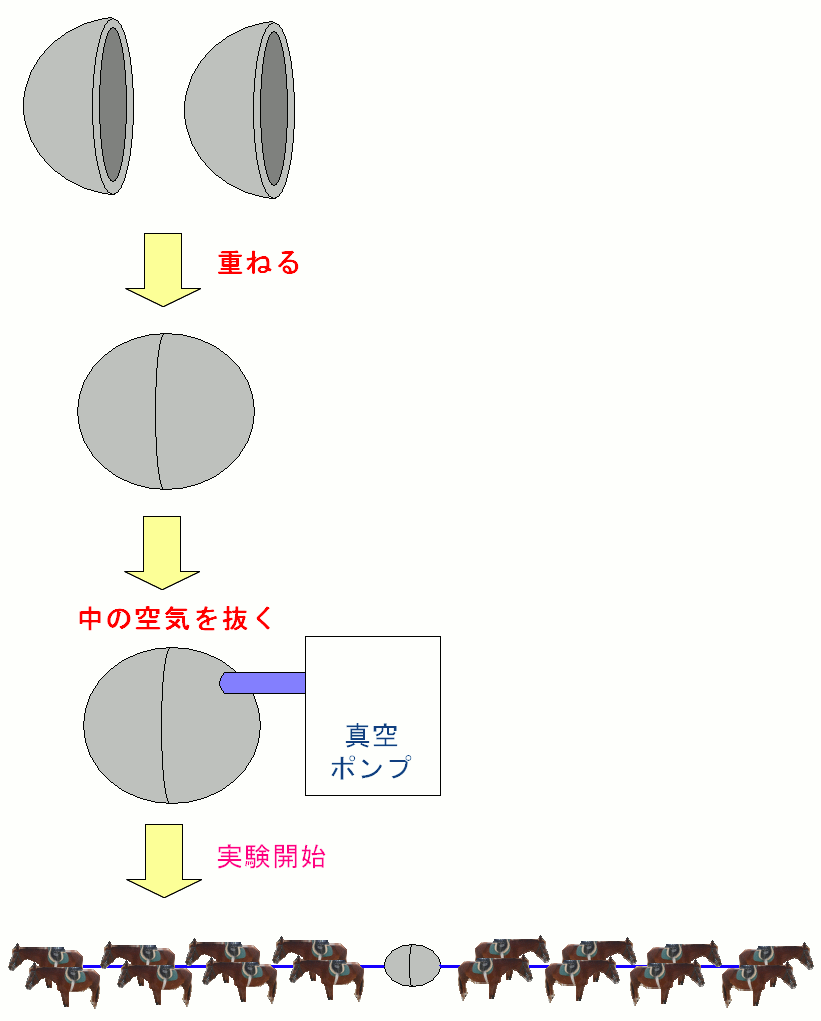
余談になるがゲーリケは真空の研究でも有名だ。 ドイツの切手に現れた科学者、技術者達(6)オットー・フォン・ゲーリケ(PDF)
| 大気圧の強さを示す実験 |
|---|
 |
|
1654年、2つの半球を重ねあわせて真空にして 両側に馬8頭で引っ張らせて、ようやく半球を引き離す事ができた実験は有名だ。 真空ポンプを発明した事で、真空放電が可能になり、 のちの蛍光灯の開発をはじめ、電磁気の発展につながったのだ。 |
ちなみに、上の実験は神聖ローマ皇帝フェルディナント3世の前で行なわれたという。 ゲーリケは科学者でもあり政治家でもあったため、政治活動をしながら 科学を見せて、科学を広めた(自分の能力の誇示?)と考えられる。 ところでゲーリケは、1660年に摩擦による摩擦発電機を発明した。 平賀源内のエレキテルの原型なのだ。 この時点では、静電気は帯びるけど、電気が流れるという考えまでには至っていなかった。 1729年、イギリスのグレイによって電気伝導が発見された。 金属だと電気が逃げるが、非金属だと電気が逃げないという話だ。 もともとは静電気が長い棒の端に静電気を与えた場合 反対側の端にも静電気が帯びる実験がキッカケだった。
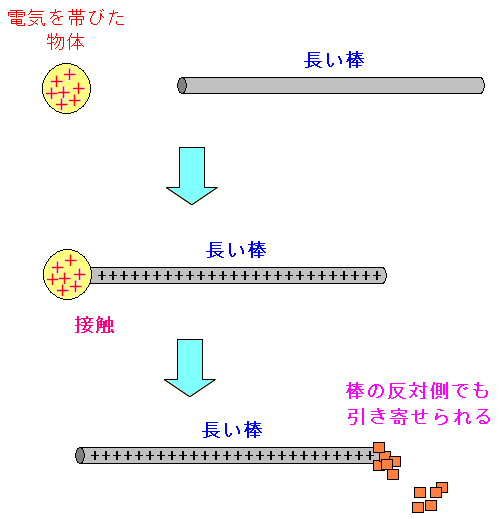
| 長い棒の端に静電気を与えると、反対側でも静電気が伝わる |
|---|
 |
|
長い棒の端に静電気を与えると、それが棒の中を伝わり 反対側の端にも静電気が帯びるため、紙などが引き寄せられる実験をした。 |
長い棒をもっと長くして、紐か何かで支える必要が出てきた。
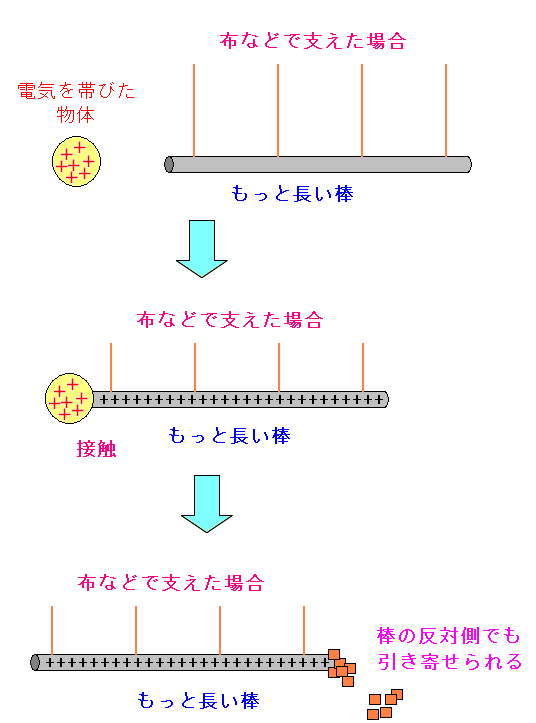
| 布などで棒を支えた場合 |
|---|
 |
|
紐は電気を通さないから、長い棒に静電気が帯びるため 棒の反対側の端でも、紙などが引き寄せられる。 |
だが、支える物を針金にすると状況が変わる
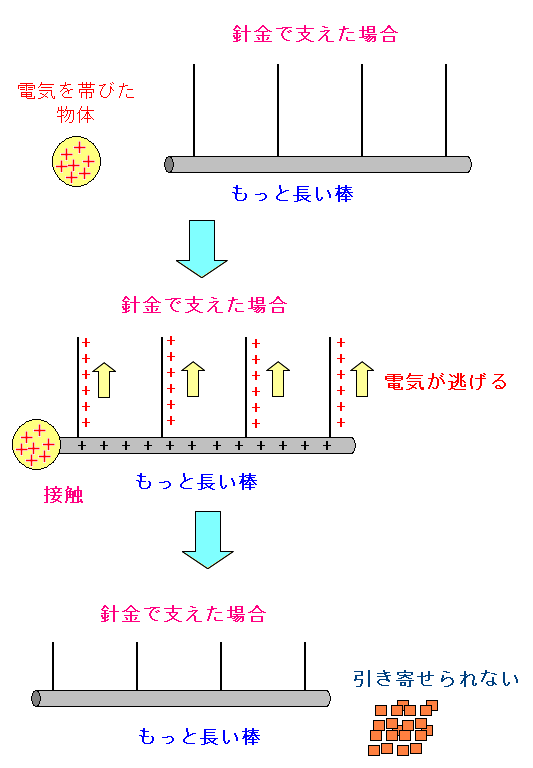
| 針金で棒を支えた場合 |
|---|
 |
|
針金は電気を通すため、針金から電気が逃げてしまい 棒は静電気がなくなってしまう。 そのため紙などを引き寄せなくなるのだ。 |
物質によって電気を通すか通さないかを調べるのが
実験が目的ではなかったのだが、結果的に
電気を流すのが導体、流さないのが絶縁体
を発見したのだ。
今でこそ、電気にプラス・マイナスがあるのが当たり前だが
この当時は、当たり前でなかった。
1733年、デュ・フェが摩擦によって生じる電気には二つの性質がある事を発見したのだ。
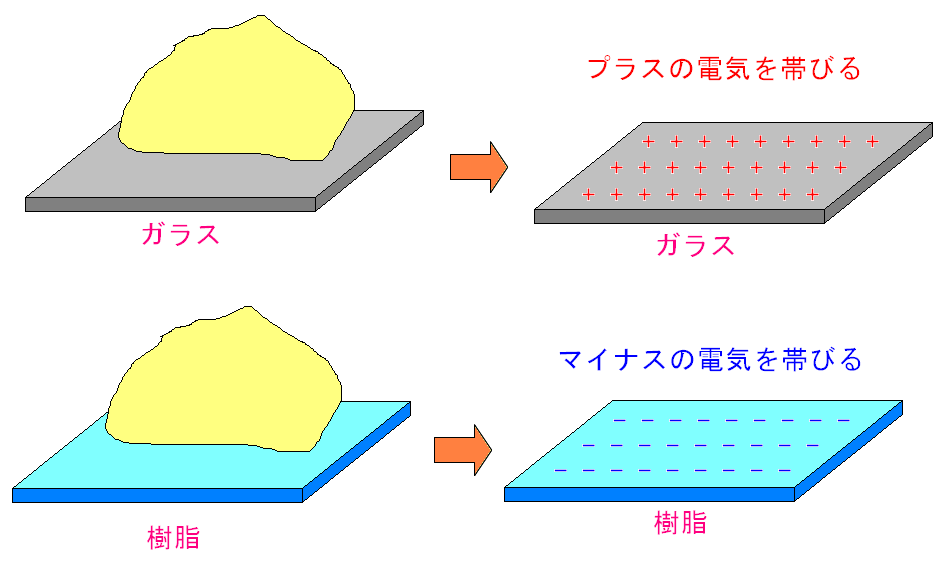
| 材質によって電気の性質が異なる |
|---|
 |
|
ガラスを布で擦った場合、プラスの静電気を帯びる 樹脂の場合は、マイナスの静電気を帯びる だが、当時はプラス・マイナスの基準がなかったので ガラス電気、樹脂電気という言い方をしていたようだ。 材質にとって異なる静電気を帯びる事がわかったのは お互いを近づけて斥力になるか引力になるかで 電気の性質の違いを発見したのだという。 |
1746年、ドイツのクライストによってライデン瓶が発明される。 ライデン大学で発明されたので、ライデン瓶というのだ。 決して、フランクリンが雷実験に使った瓶という事で 雷電(らいでん)瓶 と名づけられたのではないのだ。 ライデン瓶とは、摩擦によってできた電気を溜める装置だ。 今でいうコンデンサーと同じ原理で、家庭でも簡単にできる。 愛知県総合科学博物館 静電気であそぼう!? ところで先ほど出てきたドイツのゲーリケは、1660年には摩擦による摩擦発電機を発明した。 1746年にライデン瓶が発明された。ライデン瓶つき摩擦発電機が日本に伝わり、 平賀源内のエレキテル(1776年)になったのだ。 ここで初めて気づいた。 歴史はつながっているやん!! 学校では平賀源内のエレキテルは歴史で習い 摩擦発電機やライデン瓶は理科で習うため、科学史が好きな人でないと こういった知識は、なかなかつながらない。 ところで「ライデン瓶の発明」とサラっと書いたのだが、 ガラス技術の進歩がないと生まれなかった。 透明なガラスの発明、そして瓶の形状にする技術。それを安価にする技術。 今でこそ100金で買えるの物でも、当時はなかったり、あっても高価すぎて手がでない物もある。 なので科学史を見る際には 今では当たり前でも当時は違う という事を認識しないと、視点がおかしくなるのだ。 そして、なんで、こんな事が、わからへんかったのかという事柄は 実験のための技術も器具もなかった のが推測できる。 科学の進歩と技術の進歩は二人三脚なのだ。 1750年、電気量を測る検電器が発明される。 はく検電器という物だ。
| はく検電器 |
|---|
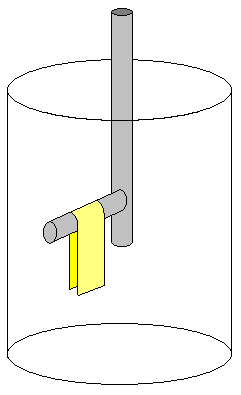 |
| 薄い金属の板をぶらさげている。 |
そこに静電気を帯びた物を持ってくる。
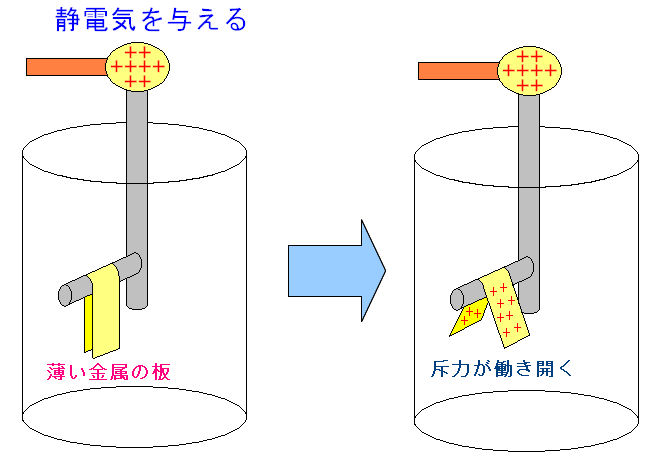
| はく検電器による電気量の測定方法 |
|---|
 |
|
静電気が薄い金属の板に帯電した時、斥力が働き、開いた状態になる。 開き度合いが大きければ、静電気の量が多い事になる。 |
そういえば・・・
中学か高校の理科実験で見た記憶が!!
不確かな記憶なのだが、理科の実験で見た記憶が出てきた。
はく検電器による電気の測定は、高校の物理の実験であるようだ。
MAkasaka's Homepage | 高校ぶつり実験 | 箔検電器による静電誘導実験
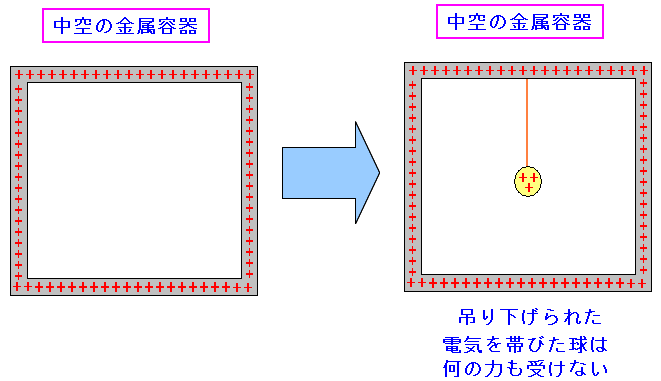
1766年、イギリスのプリーストリーが中空の導体内では
何の力も作用しない事を発見した。
| 中空の金属容器内は何の力も作用しない |
|---|
 |
|
金属容器の表面に電気が帯びていても、中の空洞では 何の力も作用しない。これを静電遮蔽という。 |
そこから万有引力の式から類推して、電気力は距離の2乗に反比例すると予想した。
とネットや資料の受け売りを書いてしまったのだが
なんで距離の2乗に反比例するねん!!
万有引力に話が飛んだ上、距離の2乗に反比例という
論理の飛躍についていけない私。
調べてみると球殻というのが出てきた。
文字通り、球面だけ殻に覆われた物体なのだ。
地球を球殻と考えた場合、表面は重力がかかるが
球の空洞には力(重力)がかからないのだ。
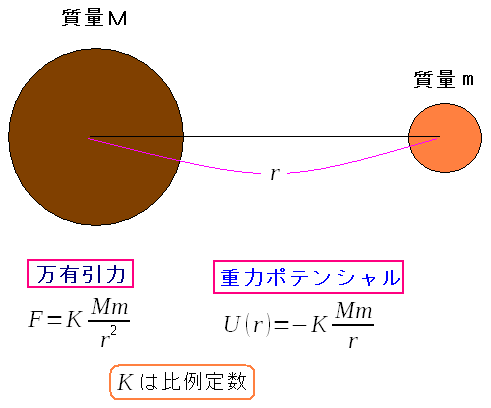
| 万有引力の法則と式 |
|---|
 |
|
質量を持つ物同士が引き寄せあうのが万有引力 当時、万有引力は質量の積と、距離の2乗に反比例しているのは わかっていた。ただし、重力定数は、1798年にキャベンディッシュによって 測定されるまでは、わからないままだった。 なので、ここでも比例定数Kとした。 |
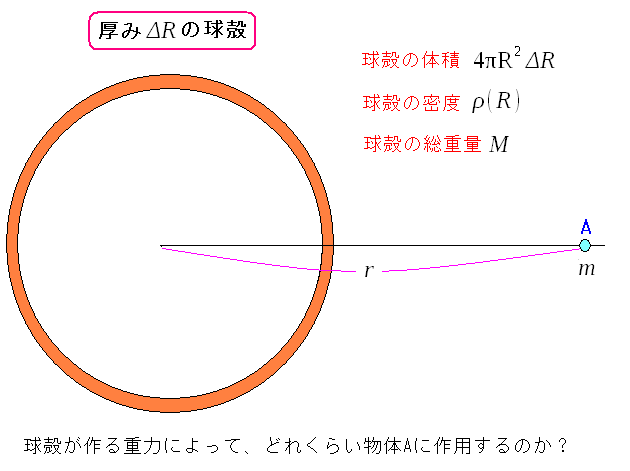
球殻が作る重力を求めてみる。
| 球殻が作る重力を求めるための準備 |
|---|
 |
|
球殻の体積、密度がわかれば、球殻の重量がわかる。 そして球殻の中心から、距離rだけ離れた地点に 質量mの物体があるとする。 |
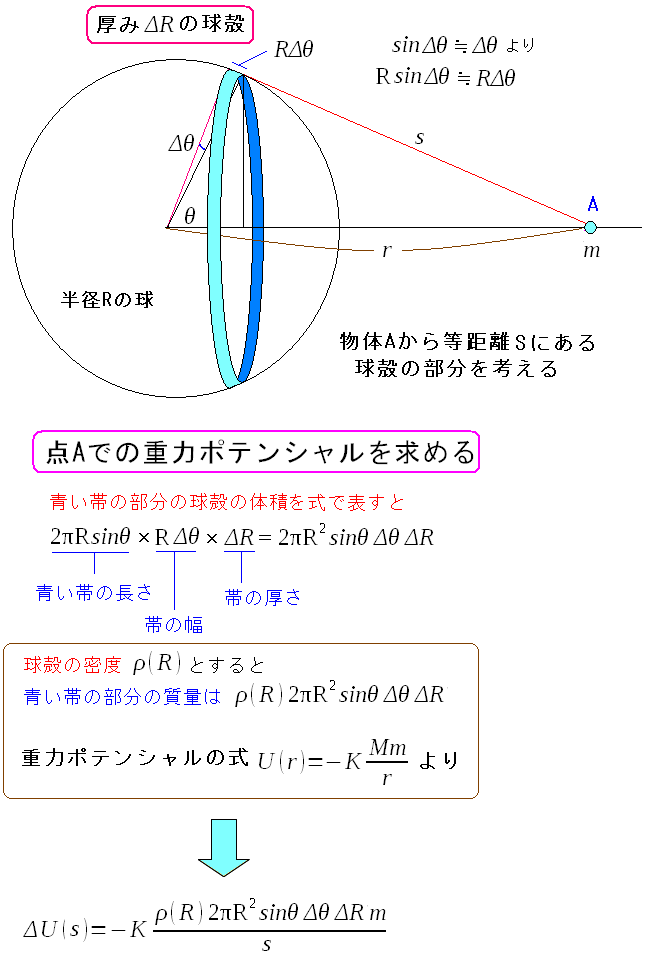
球殻と質量mの物体Aとの間でできる重力ポテンシャルを求める。
| 物体Aが球殻の外にある場合 |
|---|
 |
|
球殻の一部を帯にして、その帯の重量を求める。 その帯と物体Aで作る重力ポテンシャルを求める。 (2017/2/25訂正) 読者の方から、上図に間違いを指摘していただきました。 現在は修正済みです。間違いを指摘してくださった方には感謝します。 |
重力ポテンシャルを求めるには訳がある。
その理由は・・・
単に計算が楽だから
なのだ。
ポテンシャルはスカラーなので、重ね合わせの原理を使う場合
単純に足せば良い。
だけど、万有引力の場合、力は方向を持つベクトルなので
方向を考慮した重ね合わせの原理を使う必要がある。
重力ポテンシャルを求めた後、微分して万有引力を
求めた方が楽なのだ。
これこそ忍法「手抜きの術」なのだが、単に私が手抜きしたいだけであって
本当に、当時の物理学者は、こんな手抜きをしたのかは謎だ。
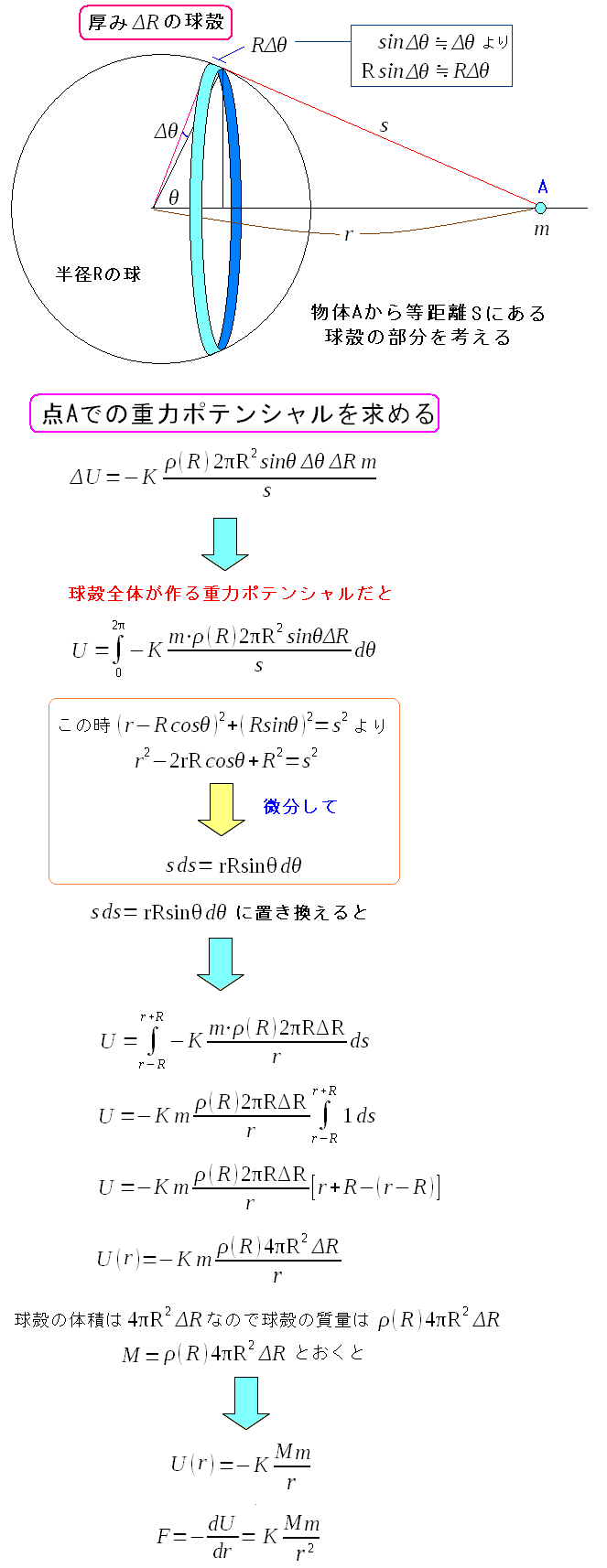
球殻の帯を積分して、球殻全体の質量と物体Aで作る
重力ポテンシャルと万有引力を求める。
| 球殻の帯を積分 |
|---|
 |
|
重力ポテンシャルと万有引力が求まった。 距離rの関数になっている。 (2017/2/25訂正) 読者の方から、上図に間違いを指摘していただきました。 現在は修正済みです。間違いを指摘してくださった方には感謝します。 |
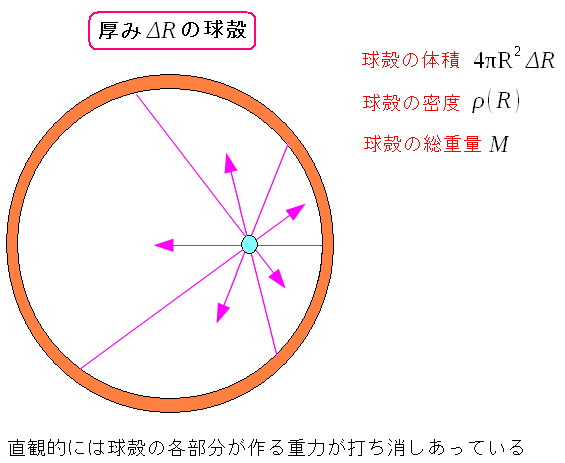
次に、物体Aが球殻の内部にある場合を計算してみる。 直観的に見ると、球殻の中は重力が打ち消しあって 重力がゼロになるように思える。
| 直観的に考えると球殻の中は力がゼロになる |
|---|
 |
|
球殻の各部分の質量と物体Aとの引き付けあう力が 打ち消しあって、重力がゼロになるように見える。 |
だが、直観だけでは判断できないので、実際に計算してみる。
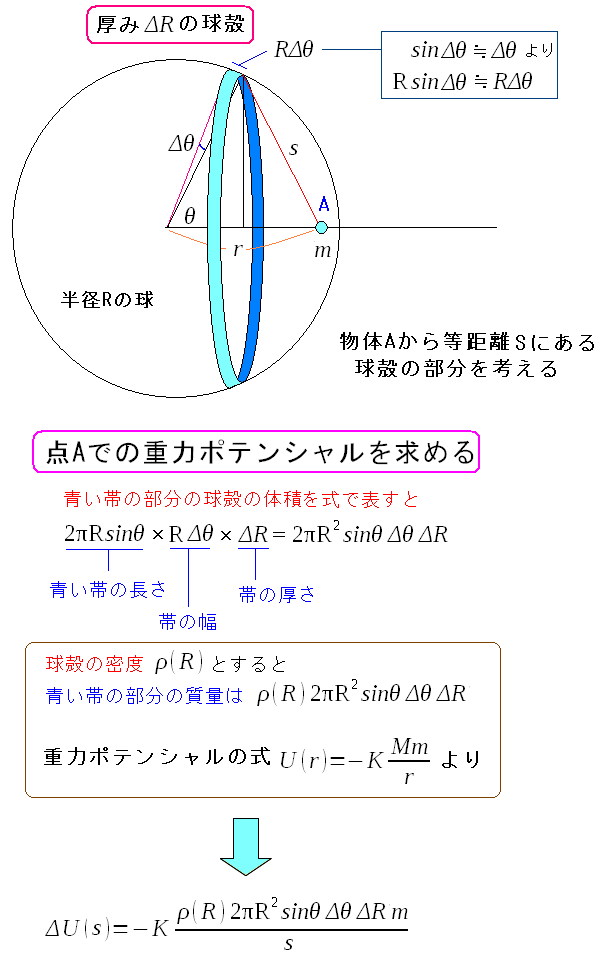
| 物体Aが球殻の内部にある場合 |
|---|
 |
|
球殻の一部の帯と、物体Aとが作る重力ポテンシャルは 物体Aが外部にある場合と同じ計算になる。 (2017/2/25訂正) 読者の方から、上図に間違いを指摘していただきました。 現在は修正済みです。間違いを指摘してくださった方には感謝します。 |
そして帯を積分して、球殻全体と物体Aによる重力ポテンシャルと 万有引力を求めてみる。
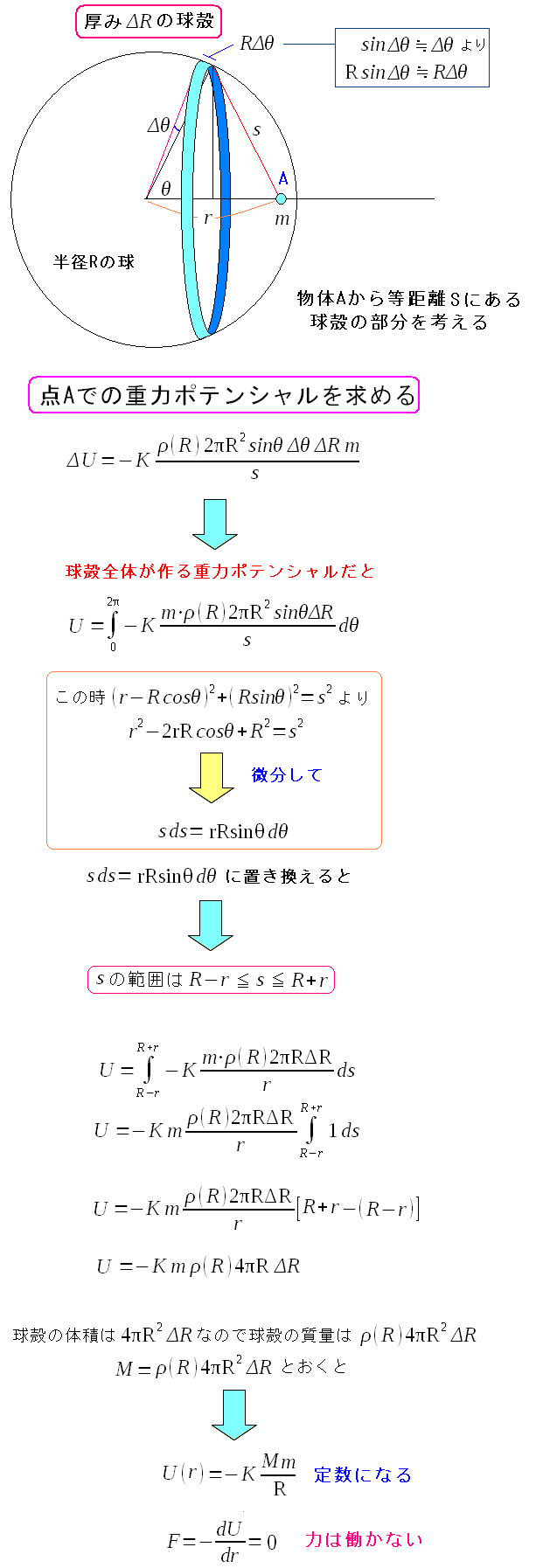
| 球殻の帯を積分すると |
|---|
 |
|
重力ポテンシャルが求まった。 距離rに依存しない定数になっている。 そして微分して求まる万有引力はゼロになる。 つまり、球殻の内部だと、何の力も作用しないのだ。 (2017/2/25訂正) 読者の方から、上図に間違いを指摘していただきました。 現在は修正済みです。間違いを指摘してくださった方には感謝します。 |
当時、本当に球殻の内部で何の力も働かない事を
実験的に確かめる事はできなかったと思うが
計算上では、力が働かない事は求められる。
電気の場合、金属の球殻の中では電気力がない事から
万有引力と同じとみなして考えると、距離の2乗の反比例になると
推測したと考えられる。
そう考えると・・・
論理の飛躍を埋めることができたのら-!!
のだ。
だが、プリーストリーは電気の力が距離の2乗に反比例と予想したが
それを実験的に確かめようとはしなかった。
クーロンが登場して、1785年に、距離の2乗に反比例する事を確かめる
実験が行なわれた。
| クーロンのねじり秤の実験 |
|---|
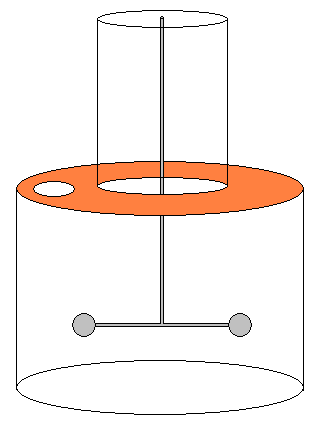 |
| 2つの小球がついた棒を吊り下げた、ねじり秤で実験を行なった。 |
ねじり秤の瓶の中に、静電気を帯びた小球を入れる。
| 静電気を帯びた小球を用意する |
|---|
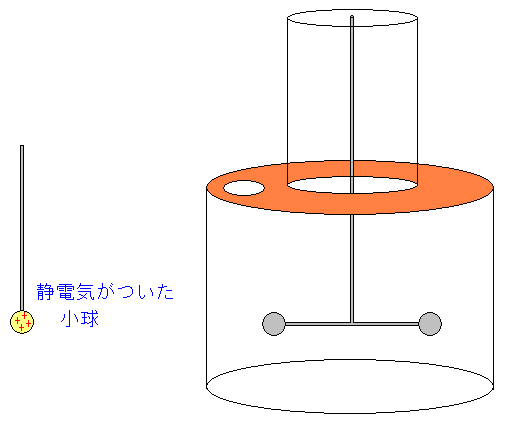 |
そして用意した静電気を帯びた小球を瓶の中に入れる。
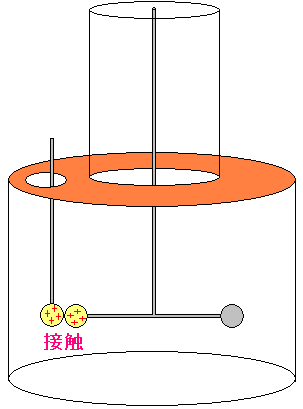
| 小球同士を接触させ、静電気を移す |
|---|
 |
|
静電気を帯びた小球を、瓶の中の小球と接触させると 静電気の半分が、接触させた瓶の中の小球に移る。 |
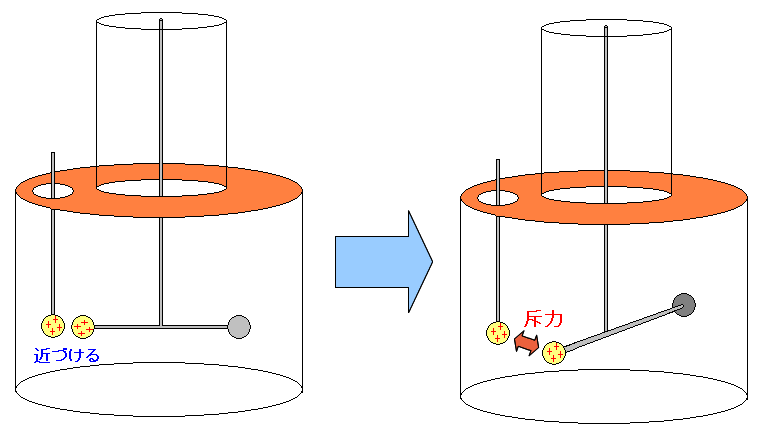
一旦、静電気を帯びた小球を取り出し、再度、瓶の中の電気を帯びた 小球に近づけてみる。
| 静電気を帯びた小球同士を近づけると斥力が働く |
|---|
 |
|
静電気を帯びた小球同士が近づくと斥力が働き 棒がねじれる。このねじれの度合いを見て 力と距離との関係を求めるのだ。 |
普通なら、ここで終わってしまう。
だが、今回は、なんで、これで・・・
力が距離の2乗に反比例するのがわかるねん!!
なのだ。
そこでクーロンが行なった実験の測定法を調べてみると
昭和47年度(第4回)の東レ理科教育賞受賞作一覧にあった。
クーロン則実験装置(PDF)
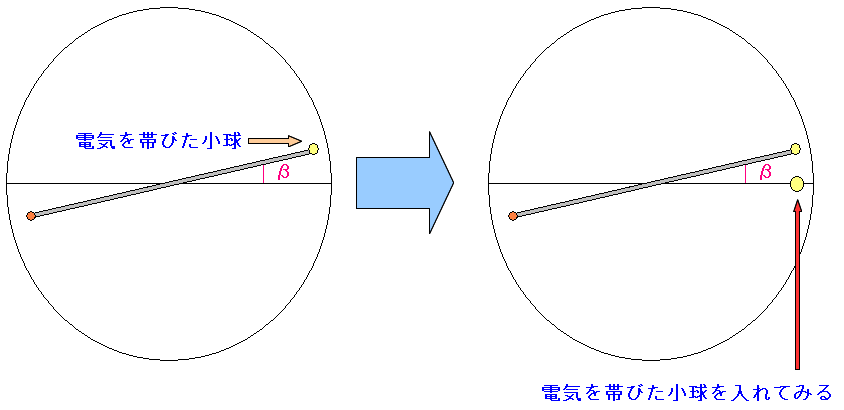
| 上から見た、ねじり秤 |
|---|
 |
|
同じ種類の電気を帯びた小球を入れる。 この時、βだけ位置をずらした所に置く。 |
すると斥力が働いて、棒にくっついた小球が移動して αだけ、ねじれる
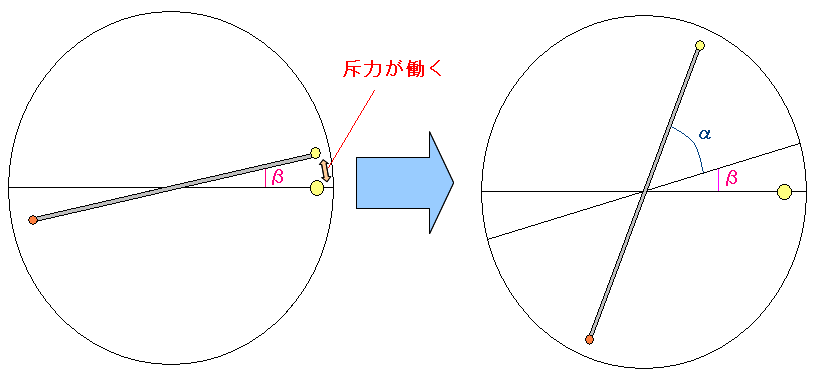
| 斥力が働き、小球がαだけ、ねじれる |
|---|
 |
|
斥力が働いたため、棒についている小球がαだけ、ねじれる。 αの所で、斥力と、ねじれの復元力がつりあう 当たり前の話だが、この原理をつかって 電気の力(斥力)が、距離の2乗に反比例するのかどうかを調べるのだ。 |
でも、これだと まだ、わからへん! なのだ。 調べるための準備が必要だ。 電気力が距離の2乗に反比例しているのを確かめるのに 何の値が必要なのか を整理する事なのだ。 それには、ねじれ秤の各部分に出てくる角度を求める必要がある。
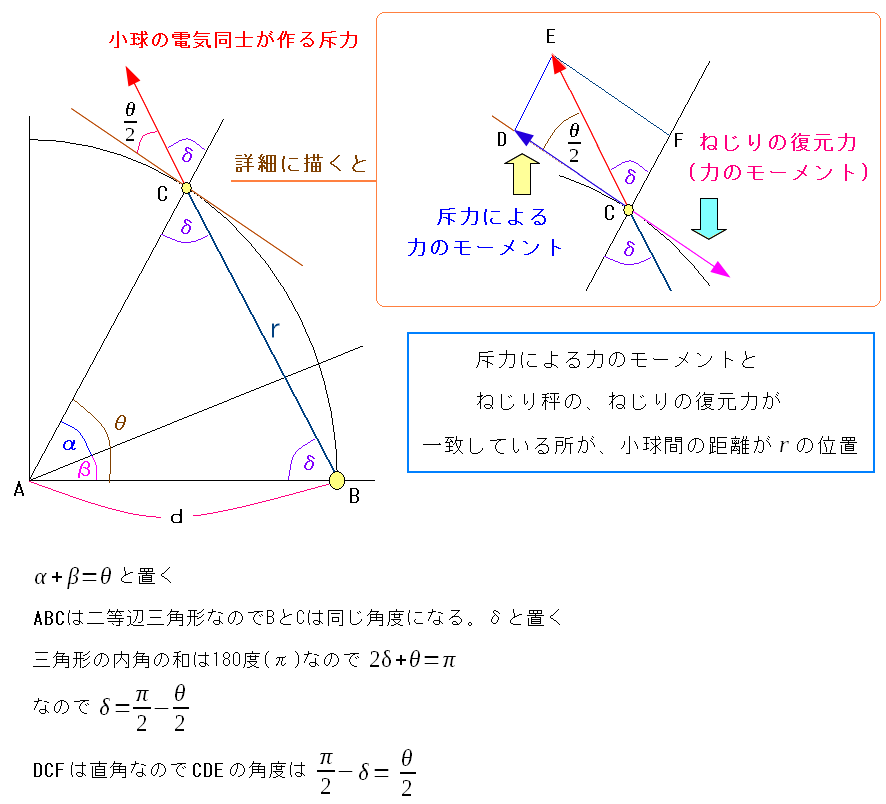
| ねじれ秤の各部分の角度について |
|---|
 |
|
斥力と小球間の距離を求めるのに、角度を知る必要がある。 そこで、全てαとθで表現できるようにした。 |
そして電気の力と、2つの小球の距離を角度αとθで表現できるようにする
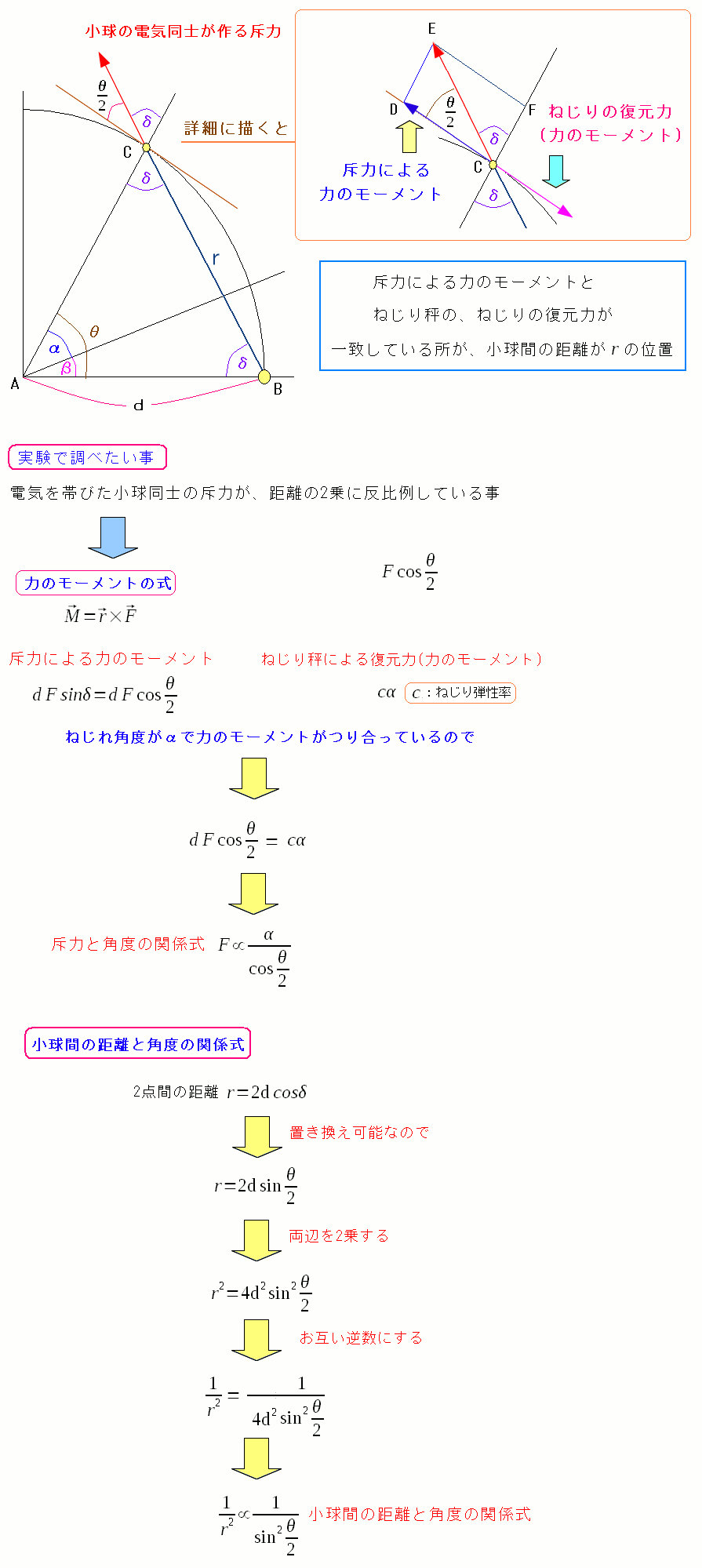
| 電気の力と、2つの小球の距離を角度αとθで表現できるようにする |
|---|
 |
|
電気の力と、小球間の距離をαとθで表現できるようにして αとθの測定だけで、電気の力と、小球間の距離を求められるようにする。 |
数学的な準備ができた所で、測定実験を開始する。
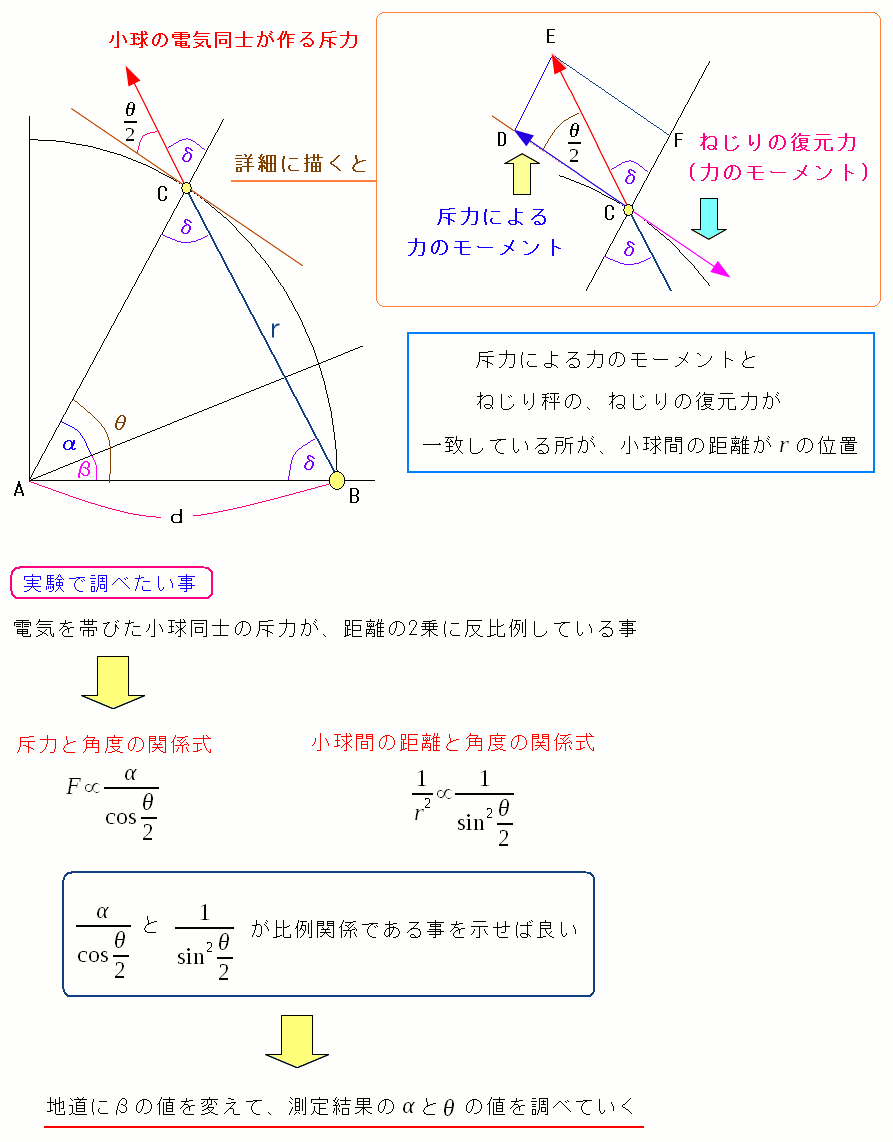
| そして角度αとθの測定実験開始 |
|---|
 |
|
地道にαとθを測定し、グラフに測定値を書いていく事で 電気の力と、小球間の距離の2乗に反比例するのがわかれば良いのだ。 この時、電荷量を求める方法もできていたので 小球の電荷量を変えながら測定する事で 電荷の積に比例している事も実験的に確認できたのだ。 |
クーロンの実験方法を知る事で
昔の人の創意工夫がわかるのだ
今みたいに精密な測定機器がない時代に、簡素な方法で
測定実験をしていくのが凄いと思う。
| 実はキャベンディッシュが第一確認者なのだが |
|---|
|
クーロン力は、距離の2乗に反比例しているのを実験的に確認したのだが 実は、それよりも前の1773年に、より精度の高い方法で確認した人がいる。 キャベンディッシュなのだ。だが、この人は、変人だったので 自分の業績を表に出さなかった。 その後、数十年後にキャベンディッシュが残した資料の整理中に クーロンよりも早く確認していたのが、わかったのだ。 ちなみに、クーロンが行なった実験と同じ方法で キャベンディッシュは1798年に重力定数を 実験的に求めているのだ。 |
そして本当に、距離の2乗に反比例で良いのか。 どこまでの精度で確認できているのか、調べてみると 相当な精度で、距離の2乗に反比例している事がわかっている。
| どこまでの精度で確認できているのか |
|---|
 |
|
自然現象なので、2乗ではなく、1.76乗や、2.13乗といった 半端な数字になっても不思議ではないのに なぜか綺麗に2乗になっている。 |
なのでクーロン力が、距離の2乗に反比例していると事で 全く問題がないので、クーロンの法則として数式で表わせるのだ。
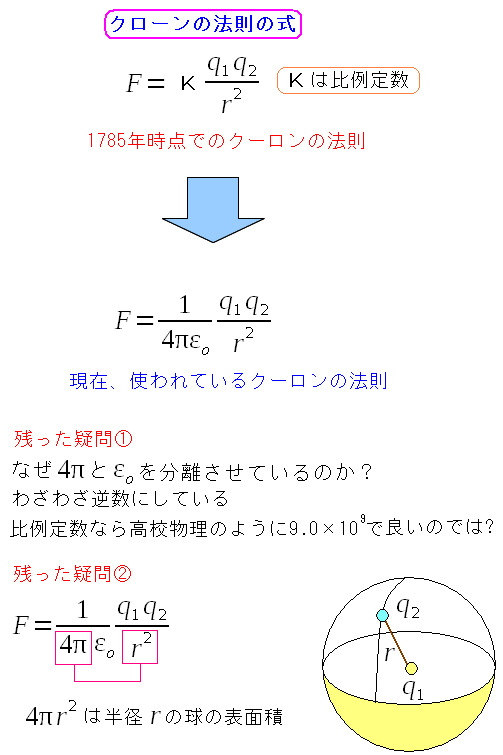
| クーロンの法則 |
|---|
 |
|
まだ比例定数が「4πεoの逆数」である疑問が残っている。 紆余曲折しながら、今の比例定数になったのだが それについては、後述しています。 |
4πやεo(誘電率)については、「電磁気学の単位系」で取り上げています。 そのため、一旦、電気の歴史の話は、ここで終わりにする。
電磁気学入門の目次
| 電磁気学入門:目次 | |
|---|---|
| スカラーとベクトル | 簡単なスカラーとベクトルの話です。 ベクトルは方向と大きさを持つ量。方向という量持っているだけに注意が必要です。 |
| 静電気の発見からクーロンの法則 | 今でこそ当たり前の静電気や導体、絶縁体、電荷など どういう経緯で発見し、クーロンの法則まで至ったのかの話です。 |
| クーロン力、電場、近接作用 | 4つの力のうち、クーロン力の位置づけ 電荷が作り出す作用の電場。近接作用の話です。 |
| 微分、全微分、方向微分 | 簡単な微分、全微分、方向微分の話です。 ここをしっかり押さえないと、電磁気の数式の意味が わからなくなります。 |
| ベクトル解析 |
電磁気に必要なベクトル解析の話です。 勾配(grad)、2次元のグリーン定理 ストークスの定理の話です。 |
| 電位ポテンシャル | 電位ポテンシャルです。勾配と電場の関係を使って説明しています。 |
| 電気双極子 |
電気双極子の話です。 物質中で起こる分極を理解するのに必要です。 |
| ガウスの法則 | ガウスの法則の積分形、微分形の話です。 |
| ポアソンの方程式、ラプラス方程式 |
ポアソンの方程式、ラプラス方程式の話です。 単に電荷分布から電位を求めるだけの話にとどまらない 奥が深い分野です。ポテンシャル論、デルタ関数 グリーン関数、固有値問題について触れています。 |
| 静電場と渦なしの法則 |
静電場で、電荷を1周させた時の仕事はゼロ 微分形と微分形の渦なしの法則の話です。 |
| ビオサバールの法則 |
電気と磁場の関係の発見の話から ビオ・サバールの法則が導かれるまでの話です。 |
| 磁気双極子 |
磁気双極子の話で、回転電流になります。 物質中の磁場の話にも関連します。 |
| アンペールの法則 |
アンペールの法則の話です。 積分形・微分形だけでなく、閉回路に流れる電流が作る 磁気双極子の話なども書いています。 |
| ローレンツ力 |
磁場中を移動する電荷にかかる力(ローレンツ力)の話です。 ローレンツ力は相対性理論が絡んでいる事も紹介しています。 |
| ファラデーの誘導起電力の法則 | ファラデーの誘導起電力の話です。 |
| うず電流を使った簡単な物理実験 | 電力計に使われるアラゴの円盤。 そしてIH調理器で熱するために発生させる、うず電流は レンツの法則から電流が発生する原理を応用した物だ。 アラゴの円盤の実験と、IH調理器を使った実験です。 気分転換で読んでください。 |
| ベクトルポテンシャル |
わかりにくいベクトルポテンシャルの話です。 電位は電荷が作る電気のポテンシャルだが ベクトルポテンシャルは電流が作る磁場のポテンシャルの話です。 |
| オームの法則の微分形 | 微小領域でのオームの法則の話です。 |
| マックスウェルの方程式 |
4つのマックスウェルの方程式を書いています。 電場と磁場の変化を図にする事で rotの回転の意味も理解できます。 |
| ゲージ変換 |
ゲージ(gauge)は物差しの意味です。 マックスウェルの方程式をE(電場)とB(磁場)の関係式から φ(電位ポテンシャル)とA(ベクトルポテンシャル)の関係式に 書き換える際、ゲージ変換が使われます。 ゲージ変換の役目を書きました。 |
| 電磁波 |
マックスウェルの方程式から電波が伝わる様子を 視覚的に見てみる話です。 |
| 回転のrotはベクトルの微分 |
ベクトル解析や渦なしの法則で出てくるrotは ベクトルの微分という話です。 |
| 電磁気学の単位系 | 電磁気学の単位系の話です。 物理量の単位系の指数を見る次元解析 電磁気学の歴史と単位系の変遷について触れました。 |
| 電気泥棒:電気と法律の話 |
電気は物体なのか、無形物なのか。 明治時代に、電気を無断で使った場合、物か、そうでないかで 窃盗罪になるかどうかが裁判で問われました。 ちょっとした科学と法律の話です。気分転換で読んでください。 |
| 数ベクトルと基底ベクトル | ベクトルの話です。 矢印だけがベクトルでない事。 数ベクトルと基底ベクトルの違いの話です。 多様体、反変・共変ベクトルを理解するのに必要です |
| 多様体 | 空間を一般化した話です。 ▽(ナブラ)の正体に迫まります |
| 外積代数 |
外積、テンソルについて書いています。 極性ベクトル、軸性ベクトル 外積は行列で、ベクトルは見せかけの姿だった話です。 |
| ベクトルの双対関係 |
反変ベクトル、共変ベクトル、双対関係 ベクトル解析、外積代数の話 外積、テンソルについて書いています。 |
| ローレンツ力と相対性理論 |
磁場は電場の相対論的効果だった話です。 ローレンツ力を使って、導線が作る磁場を使って説明です。 |
| 微分形式 |
多様体の話の続きです。 座標に依存しない形での関数やベクトルの微分の話です。 ガウスの法則、アンペールの法則、マックスウェルの方程式が 鮮やかな形で表現できます。 ∇(ナブラ)の正体もわかります。 |
| 物理と対称性 |
マックスウェルの方程式をよく見ると対称性があります。 物理の方程式と対称性を数学的な観点でみると 意外なつながりがあるという話です。 |
| マックスウェルの応力 |
電気力線を弾性体(ゴム)とみなして、力の伝わり方などを 説明した考え方です。 |
| 電場エネルギー | 電場が持つエネルギーの式を導いた話です。 |
| 磁場エネルギー |
磁場が持つエネルギーの式です。 手抜きの説明と、直流RL回路を使った説明を書きました。 |
| ポインティングベクトル |
電磁エネルギーの流れ「ポインティングベクトル」の話です。 電磁波でもエネルギー保存則が成り立つ話から ポインティングベクトルを導いています。 |
| 電気エネルギーは導線の外を伝わる |
導線の外を電気エネルギーが流れる話です。 私が誤解した事、その誤解を解いていく過程を紹介しながら 「目からウロコ」にたどり着いた話です。 |
| 物質中の電場 | 物質中の電場の話です。 分極の話をしながら、物質中の電場の話をします |
| 物質中の磁場 | 磁性の話をしながら、物質中の磁場の話をします |
| 物質中のマックスウェルの方程式 | 物質中でもマックスウェルの方程式が成り立つ話です。 |
| 導体に侵入する電磁波 |
導体に侵入する電磁波が減衰していく話です。 表皮効果と同じ「表皮の厚さ」が出てきます |
| 表皮効果 |
目的の表皮効果の話です。 マックスウェルの方程式を解きながら 交流電流の周波数を上げると、表面にしか電流が流れなくなる話です。 |