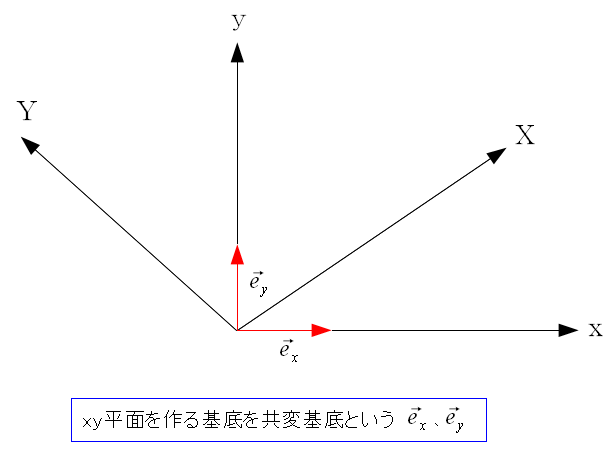
それぞれの基底を持ったxy平面とXY平面をあるとする。
xy平面を構成する基底ベクトルを、共変ベクトルという。
ただ、共変基底の定義は特になく、最初に決めた規定を
共変基底を言ったりする。
そのためXY平面の基底を先に決めてしまえば
XY平面の基底ベクトルを共変基底になるのだ。
システム奮闘記:その105
(2016年5月22日に掲載)
共変ベクトル、反変ベクトル
ところでベクトル空間には双対関係がある。 もちろん・・・ 双対って何やねん なのだ。 そしてベクトルにも極性ベクトル、軸性ベクトル以外にも 共変ベクトルと反変ベクトル があるのだ。 もちろん・・・ 共変ベクトルと反変ベクトルとは何やねん!! なのだ。 これらのベクトルの基底の事を 反変基底と反変基底なのだ! わけがわからん。 ベクトル解析やネットなどを見ても・・・ わけがわからへん だった。 だが、理解できなかった原因がわかった。 前述してる数ベクトルが何かを理解していなかったのだ。
| 編集作業状態がバレバレ |
|---|
|
いかにも章の並びが順番に並べているようだが 編集中、そんな体系的に調べて、これを書いていたわけではない。 行ったり来たりなど繰り返しながら書いていたのだ。 なので、章では前の方に置いている内容は 実は、後になって理解して、「これを書かないわけにはいかん」で 追加して書いていたりするのだ。 |
まずは共変基底から見てみることにする。
| 共変基底 |
|---|
 |
|
2次元を例にした。 それぞれの基底を持ったxy平面とXY平面をあるとする。 xy平面を構成する基底ベクトルを、共変ベクトルという。 ただ、共変基底の定義は特になく、最初に決めた規定を 共変基底を言ったりする。 そのためXY平面の基底を先に決めてしまえば XY平面の基底ベクトルを共変基底になるのだ。 |
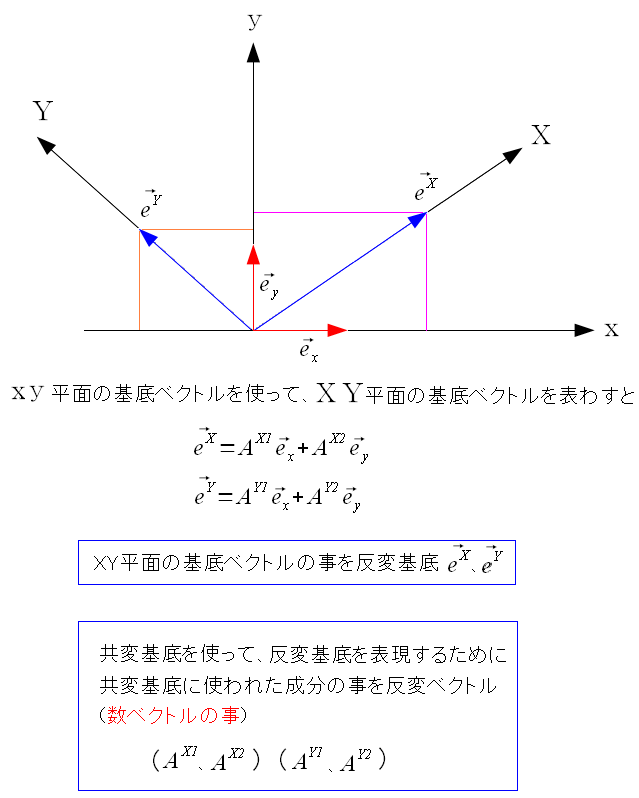
次に反変基底を見てみる。 この時、同時に反変ベクトルも同時にわかる。
| 反変基底と反変ベクトル |
|---|
 |
|
先にxy平面の基底ベクトルが決まったので、xy平面の基底を共変基底という。 あとで決めたXY平面の基底ベクトルを、反変基底という。 反変基底を、共変基底を使って表現する際の共変基底の成分を反変ベクトルという。 共変と反変を区別するため、共変の場合、添え字を下にする。 反変の場合は、添え字を上にするのが習慣だ。 |
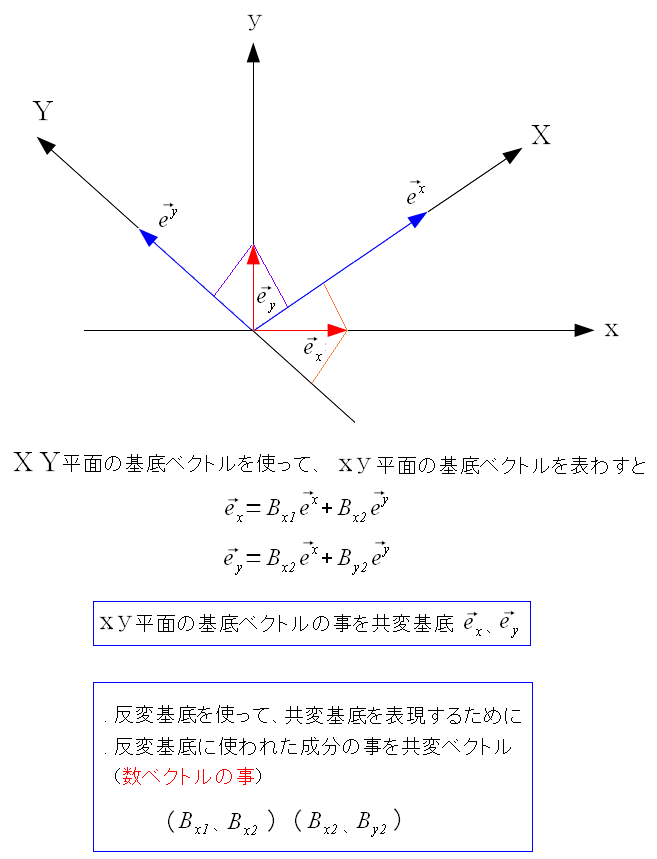
今度は共変ベクトルが何を見てみる。
| 共変ベクトル |
|---|
 |
|
共変基底を、反変基底を使って表現する際の、反変基底の成分を共変ベクトルという。 |
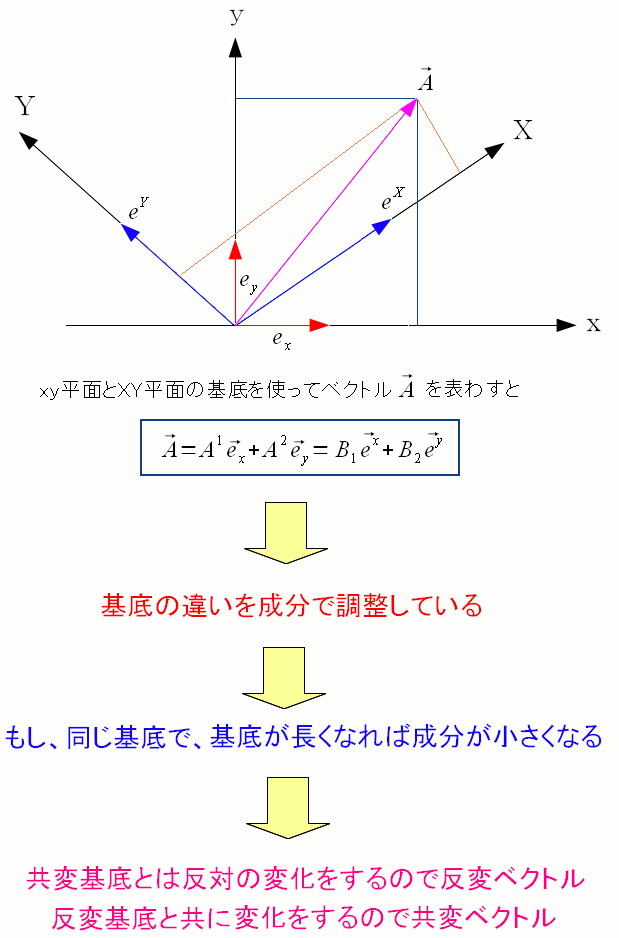
反変基底の成分(数ベクトル)は共変ベクトル。 共変基底の成分(数ベクトル)は反変ベクトル。 混乱しそうなのだが、意味は単純のようだ。 キチンと調べたわけではないので、確実ではないが 以下の説がある。
| 共変・反変の名前の由来(ある説) |
|---|
 |
|
基底ベクトルと成分(数ベクトル)で長さを調整している。 最初に決めた共変基底を長くすると、成分は小さくなる。 共変基底とは反対の変化をするので反変ベクトルになる。 反変基底を長くすると、共に変化するので共変ベクトルになる。 うそのような話だが、こういう説があるのだ。 |
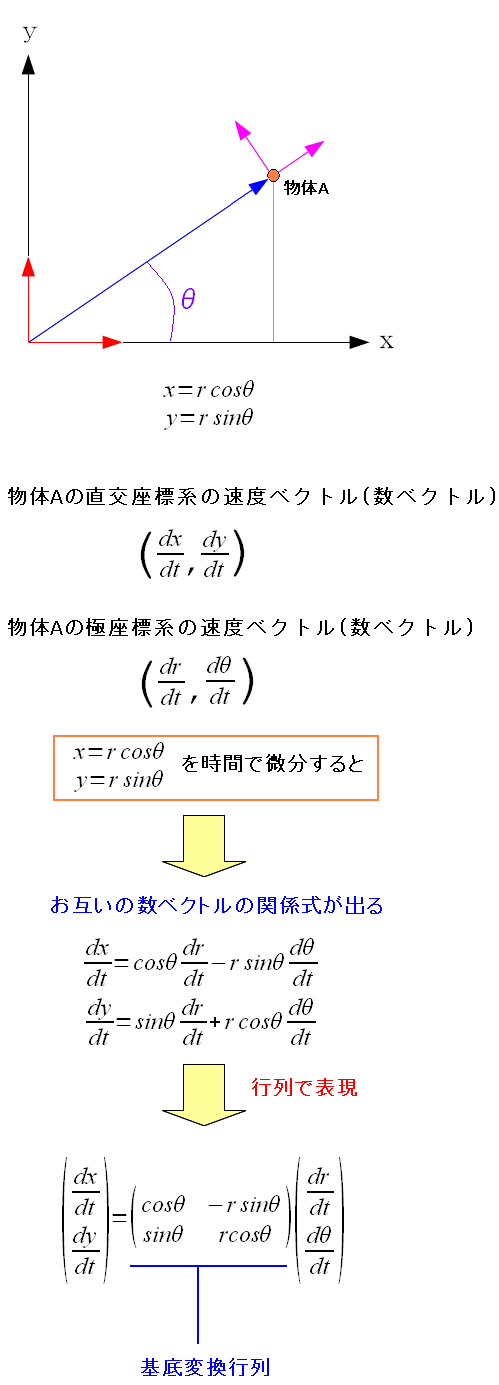
そして、気づいた 基底ベクトルの長さは自由に決められる!! 正規直交座標系で慣れ親しんでいると、基底ベクトルは長さ「1」となる。 もちろん、それで正しいのだが、これだけでは不十分だ。 なぜなら 長さ「1」そのものも自由に決めている のだ。 何を基準にするかで、長さ「1」も変わってくる。 長さだと、1mかもしれないし、1Kmかもしれないし、1光年かもしれない。 1フィートを基準にした場合だと、メートル換算すると0.3mになるのだ。 絶対的な物の長さを計る際、長さの基準を変えると、調整が必要になるのだ。 1m=3.3フィートという感じだ。 ところで、もっと当たり前の事に気づく。 なんで2つの基底がいるねん? 同じ平面なので、基底は1つだけで済むはず。 でも、よく考えると、直交座標系が表わすよりも 斜交座標系や、極座標系で表わした方が都合が良い事がある。 単に反変基底と共変基底は、2つの基底の比較であって 2次元(平面)、3次元(空間)に、2つだけの基底があるというのではない。 ところで、直交座標系上のベクトルを、斜交座標系や極座標系で表わす場合 それぞれの基底の長さに合わせながら、直交座標系の成分から、 それぞれの成分変換する必要がある。 その時の変換を 基底変換 なのだ。 数ベクトルと基底ベクトルの復習として、簡単な例で、極座標系の数ベクトルから 直交座標系の数ベクトルの変換する方法を見てみる。
| 極座標系から直交座標系への数ベクトルの変換方法 |
|---|
 |
|
物体Aが、ある速度で動いているとする。 直交座標系と極座標系の速度ベクトルがある 直交座標系と極座標系の点の関係式があるので そのまんま、関係式を時間で微分すると、(r,θ)の地点での 速度ベクトル同士の関係式が出てくる。 お互いの基底ベクトルと数ベクトルの関係式が出てくる。 そこから基底変換のための行列を求めれば良いのだ。 基底ベクトルは隠蔽されているが、気にしなくても良い。 そのまま(r,θ)の地点での極座標系の速度(数ベクトル)を代入すると 直交座標系の速度(数ベクトル)に変換してくれるのだ。 |
上手に基底変換を使えば、便利な事があるようだ。 でも、私は、そういう便利な事に出くわした事はないのだ・・・。
双対関係と双対空間
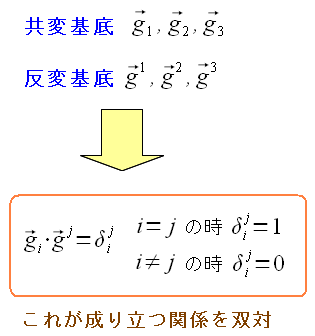
共変基底と反変基底が出てきた。 ところで双対関係とは何か。 以下のような関係を言うのだ。
| 双対関係 |
|---|
 |
|
共変基底と反変基底で、添え字が同じもの同士の内積が 「1」になり、そうでない場合はゼロになる関係だ。 |
具体的に双対関係がどういう物か見てみる事にする。
| 斜交座標系と、その基底ベクトル |
|---|
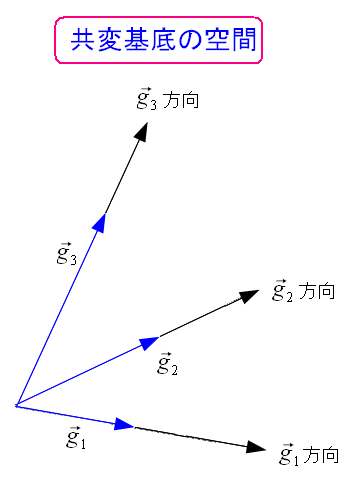 |
| 上図のような斜交座標系と、その基底ベクトルで考えてみる。 |
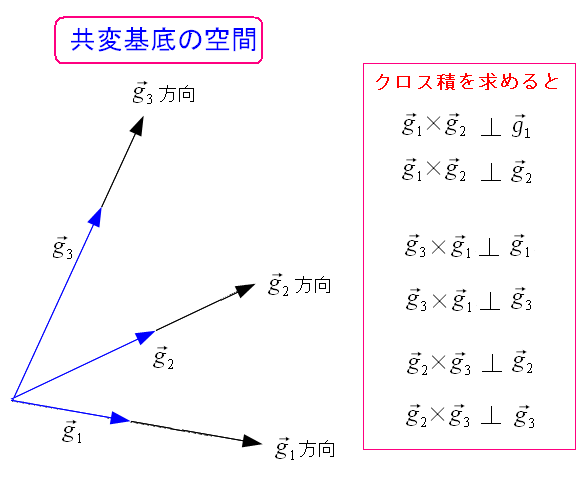
双対関係を見たした、反変基底を求める必要がある。 でも、案外、簡単に反変基底は求められる。
| 斜交座標系をよく見ると |
|---|
 |
|
斜交座標系の基底ベクトルのクロス積を取ると 当たり前なのだが、上図のような事が成り立つ。 |
そこで以下のように計算すると、双対関係が成り立つ反変基底が求まる。
| 斜交座標系の基底ベクトル(共変基底)から反変基底を求める |
|---|
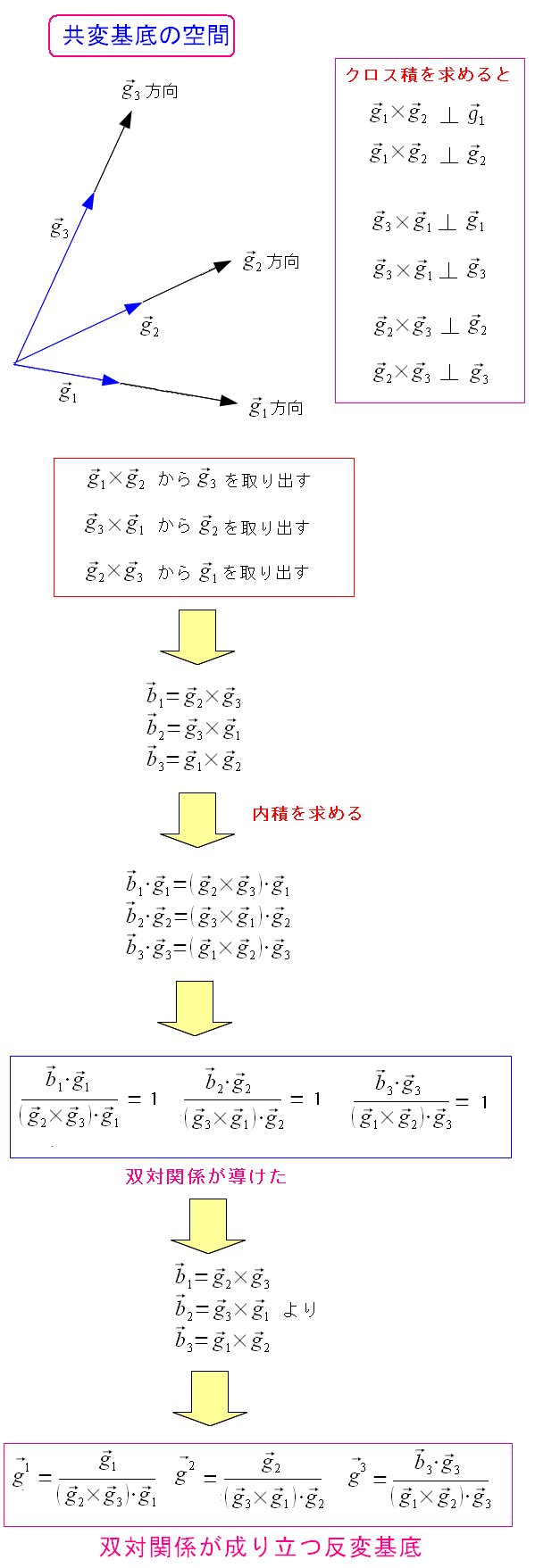 |
| あっさりと双対関係が成り立つ反変基底が求まったのだ。 |
斜交座標系の共変基底と反変基底の関係を図にしてみた。
| 斜交座標系の共変基底と反変基底の関係 |
|---|
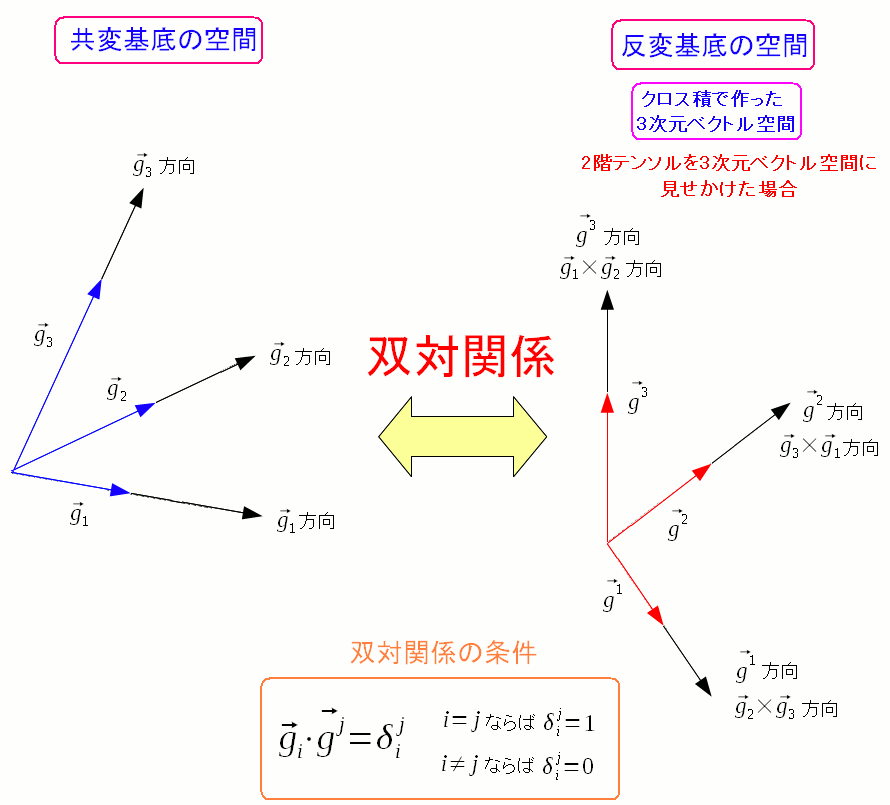 |
| 図にすると上のような感じになる。 |
そして双対関係は以下のようにも言われている
| 斜交座標系の共変基底と反変基底は鏡の関係 |
|---|
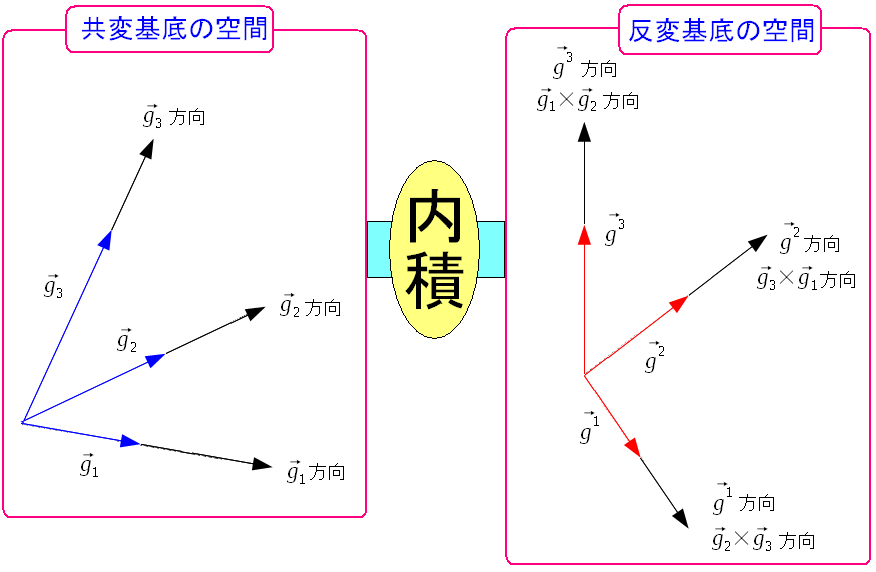 |
| 双対関係は内積という鏡を使って、お互いを写す物とも言われている。 |
これだけだと 何がしたいねん になる。私もそう思った。 だが、調べていくにつれ、わかった事は・・・ 斜交座標系だと 基底ベクトルの長さはバラバラ なのだ。 基底ベクトルの長さは、人間が自由に決められる。 正規直交座標系のように、3方向の基底ベクトルの長さを揃える必要はない。 そのため・・・ 内積が「1」になるベクトルを用意する必要がある というのだ。
| 内積の定義に必要だったかも |
|---|
|
斜交座標系の共変基底と反変基底。 今回の話では使う事がないので、深く調べていない。 内積を定義するために、反変基底を持ち出しただけかもしれない。 |
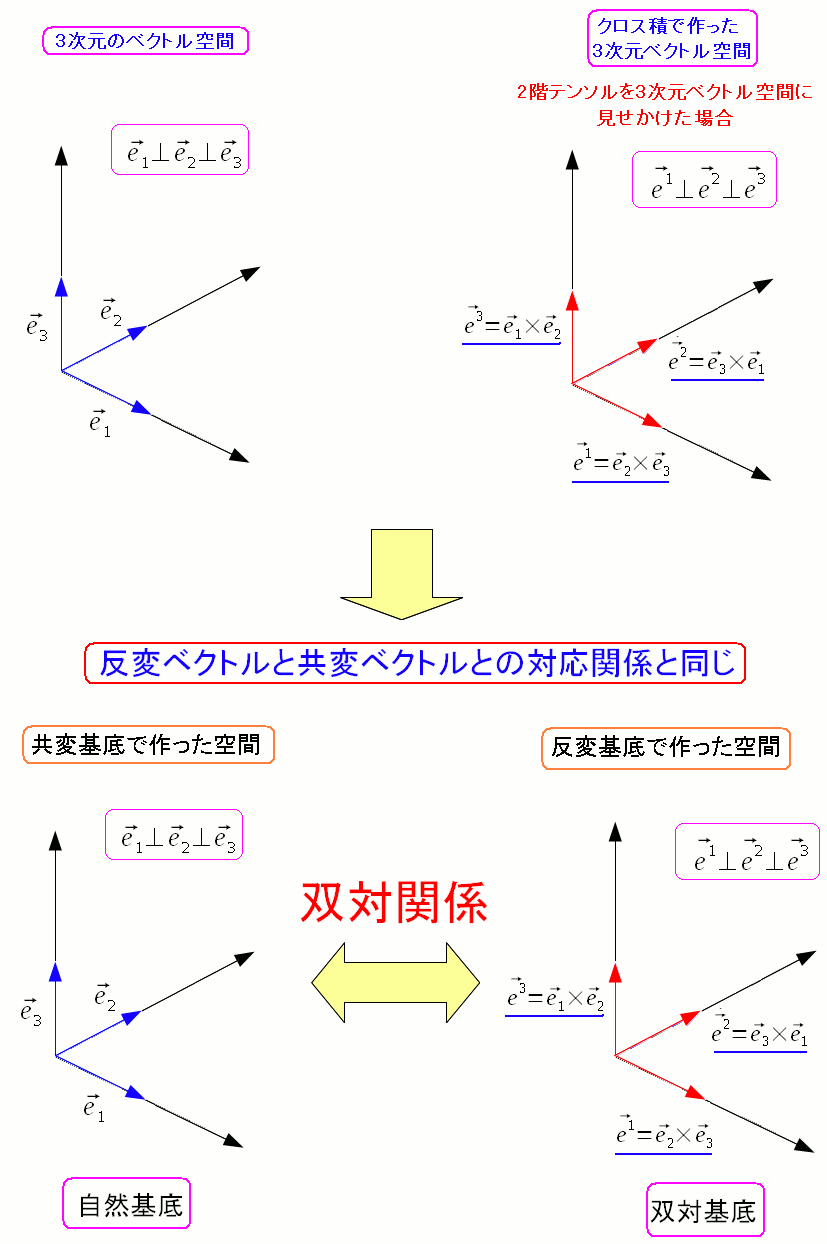
斜交座標系だけでなく、正規直交座標系でも双対関係はあるのだ。
| 正規直交座標系での共変基底と反変基底の関係 |
|---|
 |
|
元々の基底ベクトルと、クロス積で作った基底ベクトルの空間だ。 2つとも一致するため、普段は違いが見えてこない。 区別するため、元々の基底を自然基底。クロス積で作った基底を双対基底という。 |
直交座標系における双対関係。既に出てきた。 多様体の所で、少し触れたのだが、速度ベクトルの基底と 勾配ベクトルの基底が双対関係だったのだ。
| 直交座標系における双対関係の例 |
|---|
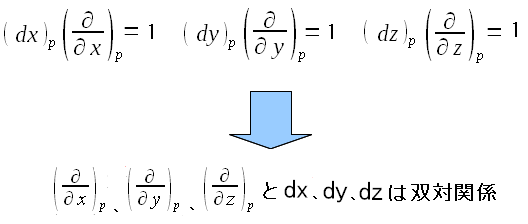 |
|
多様体上の速度ベクトルで使われている基底ベクトルと 勾配ベクトルで使われている基底ベクトルが双対関係なのだ。 |
双対関係と内積
双対関係を結びつけるのに内積が出てきた。 内積とは共変基底と反変基底の積になる。 踏み込んで考えると・・・ 1階のテンソルと2階のテンソルの積やん!! にわかに信じられない。 高校で内積を習い、大学の線形代数で外積(クロス積)を習う。 計算方法も振る舞いも異なるため、別物だと思い込んでいた。 内積の中にクロス積が含まれている というのは衝撃なのだ。 まずは3つの1階のテンソルのウェッジ積を求める。
| 3つの1階のテンソルのウェッジ積 |
|---|
 |
| 3つの1階のテンソルのウェッジ積の自由度は1なのが出てきた。 |
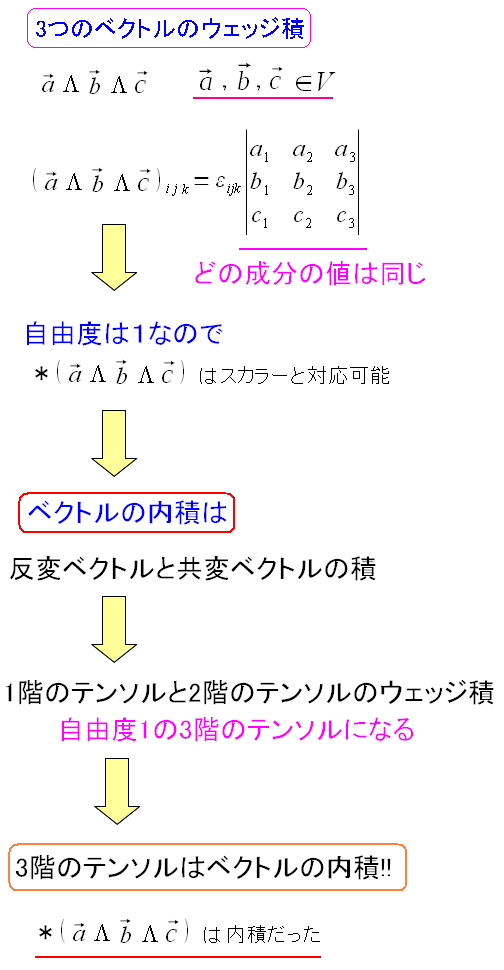
3つの1階のテンソルのウェッジ積の自由度は1。 3階のテンソルだが、実質の変数は1個。なので実数と対応関係ができる。
| 内積は3階のテンソル。だけど実数と対応可能 |
|---|
 |
|
自由度1の3階のテンソルなので、実数との対応ができる。 2階のテンソルはベクトルとみなせる事は、外積代数で説明した。 内積は1階のテンソルと、2階のテンソルの積になるのだ。 自由度1の変数こそ、内積の値になるのだ。 |
外積代数の視点から見た 内積の正体が見えた!! だが、頭の中は混乱しまくる。 正規直交座標系で、共変・反変の違いもわからずにいたため 同じベクトル同士の積が実数になると思っていた。 そのため3階のテンソルと言われると、唖然とするのだ。
電磁気学入門の目次
| 電磁気学入門:目次 | |
|---|---|
| スカラーとベクトル | 簡単なスカラーとベクトルの話です。 ベクトルは方向と大きさを持つ量。方向という量持っているだけに注意が必要です。 |
| 静電気の発見からクーロンの法則 | 今でこそ当たり前の静電気や導体、絶縁体、電荷など どういう経緯で発見し、クーロンの法則まで至ったのかの話です。 |
| クーロン力、電場、近接作用 | 4つの力のうち、クーロン力の位置づけ 電荷が作り出す作用の電場。近接作用の話です。 |
| 微分、全微分、方向微分 | 簡単な微分、全微分、方向微分の話です。 ここをしっかり押さえないと、電磁気の数式の意味が わからなくなります。 |
| ベクトル解析 |
電磁気に必要なベクトル解析の話です。 勾配(grad)、2次元のグリーン定理 ストークスの定理の話です。 |
| 電位ポテンシャル | 電位ポテンシャルです。勾配と電場の関係を使って説明しています。 |
| 電気双極子 |
電気双極子の話です。 物質中で起こる分極を理解するのに必要です。 |
| ガウスの法則 | ガウスの法則の積分形、微分形の話です。 |
| ポアソンの方程式、ラプラス方程式 |
ポアソンの方程式、ラプラス方程式の話です。 単に電荷分布から電位を求めるだけの話にとどまらない 奥が深い分野です。ポテンシャル論、デルタ関数 グリーン関数、固有値問題について触れています。 |
| 静電場と渦なしの法則 |
静電場で、電荷を1周させた時の仕事はゼロ 微分形と微分形の渦なしの法則の話です。 |
| ビオサバールの法則 |
電気と磁場の関係の発見の話から ビオ・サバールの法則が導かれるまでの話です。 |
| 磁気双極子 |
磁気双極子の話で、回転電流になります。 物質中の磁場の話にも関連します。 |
| アンペールの法則 |
アンペールの法則の話です。 積分形・微分形だけでなく、閉回路に流れる電流が作る 磁気双極子の話なども書いています。 |
| ローレンツ力 |
磁場中を移動する電荷にかかる力(ローレンツ力)の話です。 ローレンツ力は相対性理論が絡んでいる事も紹介しています。 |
| ファラデーの誘導起電力の法則 | ファラデーの誘導起電力の話です。 |
| うず電流を使った簡単な物理実験 | 電力計に使われるアラゴの円盤。 そしてIH調理器で熱するために発生させる、うず電流は レンツの法則から電流が発生する原理を応用した物だ。 アラゴの円盤の実験と、IH調理器を使った実験です。 気分転換で読んでください。 |
| ベクトルポテンシャル |
わかりにくいベクトルポテンシャルの話です。 電位は電荷が作る電気のポテンシャルだが ベクトルポテンシャルは電流が作る磁場のポテンシャルの話です。 |
| オームの法則の微分形 | 微小領域でのオームの法則の話です。 |
| マックスウェルの方程式 |
4つのマックスウェルの方程式を書いています。 電場と磁場の変化を図にする事で rotの回転の意味も理解できます。 |
| ゲージ変換 |
ゲージ(gauge)は物差しの意味です。 マックスウェルの方程式をE(電場)とB(磁場)の関係式から φ(電位ポテンシャル)とA(ベクトルポテンシャル)の関係式に 書き換える際、ゲージ変換が使われます。 ゲージ変換の役目を書きました。 |
| 電磁波 |
マックスウェルの方程式から電波が伝わる様子を 視覚的に見てみる話です。 |
| 回転のrotはベクトルの微分 |
ベクトル解析や渦なしの法則で出てくるrotは ベクトルの微分という話です。 |
| 電磁気学の単位系 | 電磁気学の単位系の話です。 物理量の単位系の指数を見る次元解析 電磁気学の歴史と単位系の変遷について触れました。 |
| 電気泥棒:電気と法律の話 |
電気は物体なのか、無形物なのか。 明治時代に、電気を無断で使った場合、物か、そうでないかで 窃盗罪になるかどうかが裁判で問われました。 ちょっとした科学と法律の話です。気分転換で読んでください。 |
| 数ベクトルと基底ベクトル | ベクトルの話です。 矢印だけがベクトルでない事。 数ベクトルと基底ベクトルの違いの話です。 多様体、反変・共変ベクトルを理解するのに必要です |
| 多様体 | 空間を一般化した話です。 ▽(ナブラ)の正体に迫まります |
| 外積代数 |
外積、テンソルについて書いています。 極性ベクトル、軸性ベクトル 外積は行列で、ベクトルは見せかけの姿だった話です。 |
| ベクトルの双対関係 |
反変ベクトル、共変ベクトル、双対関係 ベクトル解析、外積代数の話 外積、テンソルについて書いています。 |
| ローレンツ力と相対性理論 |
磁場は電場の相対論的効果だった話です。 ローレンツ力を使って、導線が作る磁場を使って説明です。 |
| 微分形式 |
多様体の話の続きです。 座標に依存しない形での関数やベクトルの微分の話です。 ガウスの法則、アンペールの法則、マックスウェルの方程式が 鮮やかな形で表現できます。 ∇(ナブラ)の正体もわかります。 |
| 物理と対称性 |
マックスウェルの方程式をよく見ると対称性があります。 物理の方程式と対称性を数学的な観点でみると 意外なつながりがあるという話です。 |
| マックスウェルの応力 |
電気力線を弾性体(ゴム)とみなして、力の伝わり方などを 説明した考え方です。 |
| 電場エネルギー | 電場が持つエネルギーの式を導いた話です。 |
| 磁場エネルギー |
磁場が持つエネルギーの式です。 手抜きの説明と、直流RL回路を使った説明を書きました。 |
| ポインティングベクトル |
電磁エネルギーの流れ「ポインティングベクトル」の話です。 電磁波でもエネルギー保存則が成り立つ話から ポインティングベクトルを導いています。 |
| 電気エネルギーは導線の外を伝わる |
導線の外を電気エネルギーが流れる話です。 私が誤解した事、その誤解を解いていく過程を紹介しながら 「目からウロコ」にたどり着いた話です。 |
| 物質中の電場 | 物質中の電場の話です。 分極の話をしながら、物質中の電場の話をします |
| 物質中の磁場 | 磁性の話をしながら、物質中の磁場の話をします |
| 物質中のマックスウェルの方程式 | 物質中でもマックスウェルの方程式が成り立つ話です。 |
| 導体に侵入する電磁波 |
導体に侵入する電磁波が減衰していく話です。 表皮効果と同じ「表皮の厚さ」が出てきます |
| 表皮効果 |
目的の表皮効果の話です。 マックスウェルの方程式を解きながら 交流電流の周波数を上げると、表面にしか電流が流れなくなる話です。 |