システム奮闘記：その105

外積代数

(2016年5月22日に掲載)

外積とテンソル

　外積代数。
　簡単に言えば

　外積の規則に従った計算する数学

　なのだ。そのまんまだ。

　ところで外積といえば積の順序を変えると符号が変わる

外積は、積の順序を変えると符号が変わる

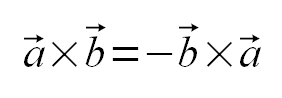ベクトルの外積は交換可能ではないのだ。


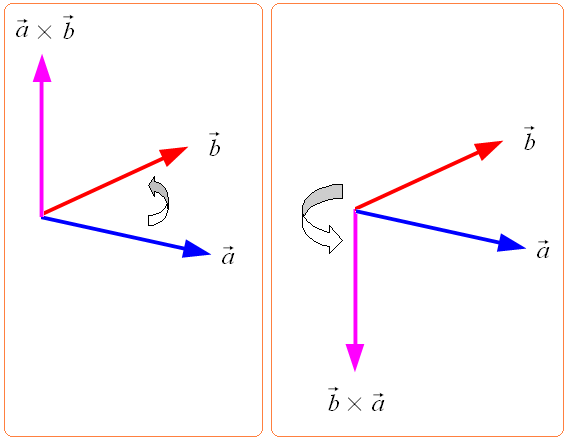
　これを図にすると以下の通りだ。

ベクトルの外積で、順番を変えると

外積の場合、順番を変えると、符号が反対になる。そういう計算規則があるのだ。


　ところで外積代数にはテンソルという概念が出てくる。
　テンソルとは何なのか見てみる事にした。

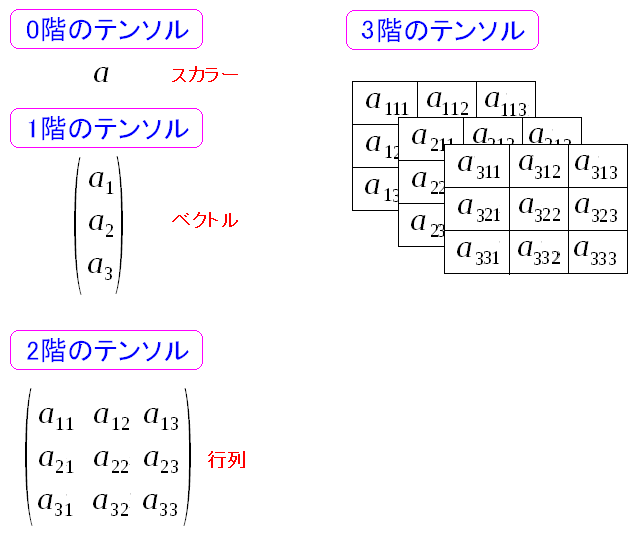
テンソルとは

0階のテンソルはスカラー。 1階のテンソルはベクトル。 2階のテンソルは行列。 3階、4階という順番に、複雑な物になっていくのだ。


　ところでテンソル同士の積には直積というのがある。

　正直な事を書くと

　直積とは何やねん!!

　なのだ。

　1階のテンソル(ベクトル)同士の直積を見てみる事にした。

1階のテンソル(ベクトル)同士の直積

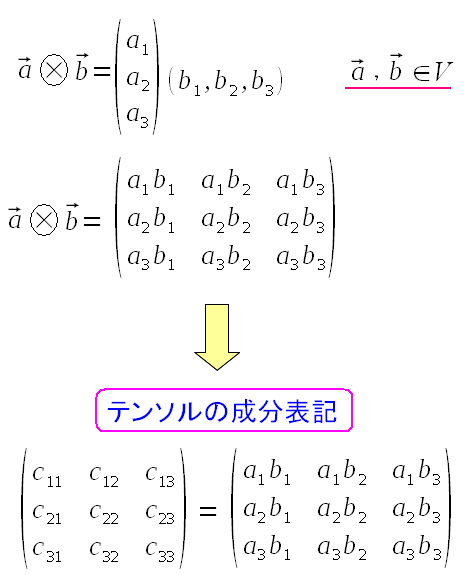
外積とは違う計算方法だ。 1階のテンソル同士の直積により、2階のテンソル(行列)ができるのだ。全部の成分の組み合わせを掛けているのだ。直積の演算記号は○の中に「×」が入った記号になるのだ。


　これも計算規則なので、覚えるしかないのだ。

1階のテンソル同士の直積により、2階のテンソル(行列)ができる

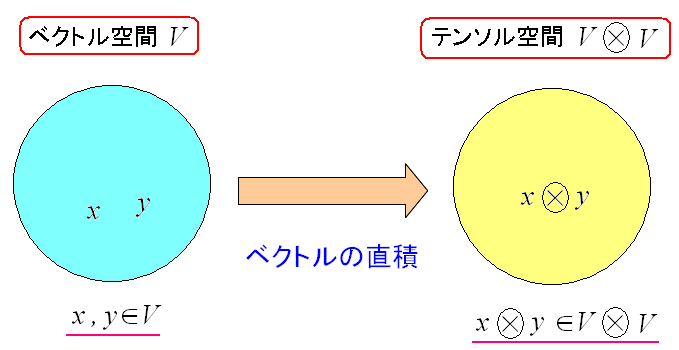直積の表記は上図のようになるのだ。


クロス積とウェッジ積

　ところで外積には2種類ある。

　ウェッジ積(楔積)とクロス積

　なのだ。

　ところで

　ウェッジ積(楔積)とは何やねん!

ウェッジ積(楔積)とは

ベクトル同士の直積と、順序を入れ替えたベクトルの直積の差がウェッジ積だ。これも計算規則なので、そのまま受け入れるしかない。ウェッジ積の事を、別名・楔積(くさび積)とも言うのだ。


　計算記号(∧)は、どっかで見た記号だ。

　微分形式で出てきた計算記号(∧)なのだ

　rotがベクトルの微分だと知る過程で、微分形式を少しかじったのだ。
　微分形式で必要となるベクトルの積なのだ。詳しくは後述しています。

　ウェッジ積の演算規則がある。

ウェッジ積の演算規則

線形代数で習うベクトルの外積に似ている。ちなみに、線形代数で習う外積はクロス積という。


　ウェッジ積を詳しくみていく。

ウェッジ積は斜めを貫く軸に対して反対称

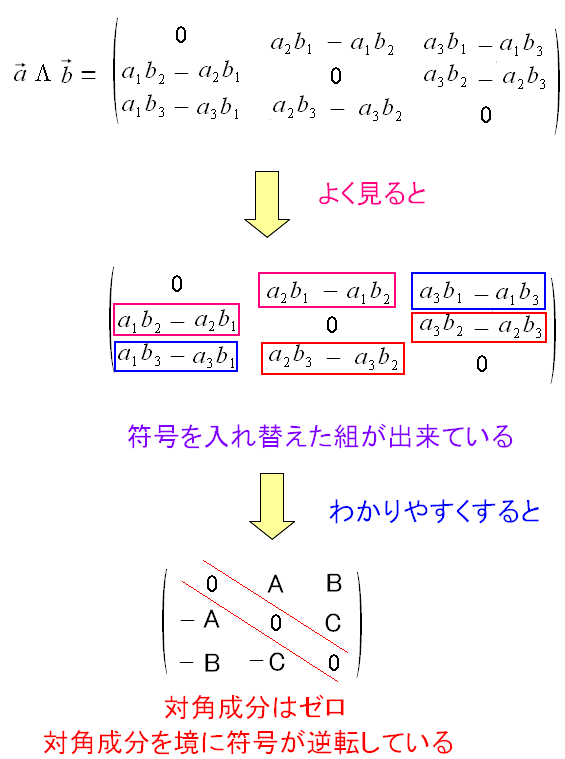
ウェッジ積を求めた際に出てきた2階のテンソル(行列)を見ると斜めを貫く軸に対して反対称になっている。


　ところで2階のテンソルには対称テンソルと反対称テンソルがある。


　まずは2階の対象テンソル(対称行列)を見てみる。

2階の対称テンソル(対称行列)

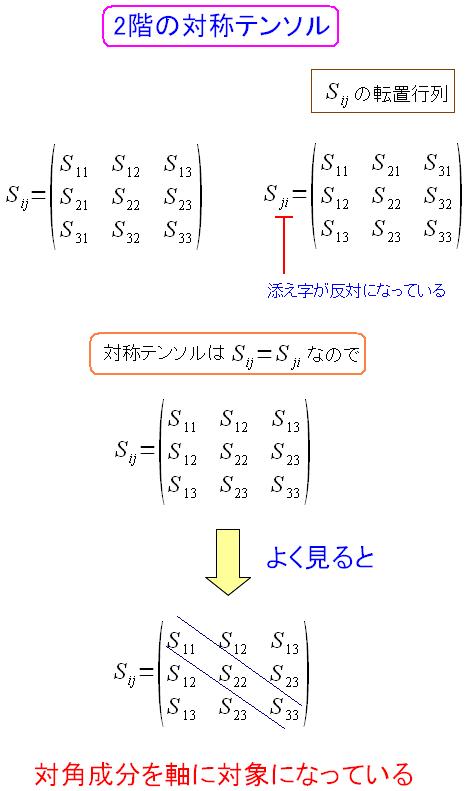斜めを貫く軸に対して対称になっている。


　次に2階の反対称テンソル(反対称行列)とはどういう物なのか、見てみる。

2階の反対称テンソル(反対称行列)

気づいた人はいると思うが、この並びはウェッジ積の並びなのだ。


　ベクトルの直積を使って、2階の対称テンソルの求め方は簡単だ。

直積を使った対称行列の求め方

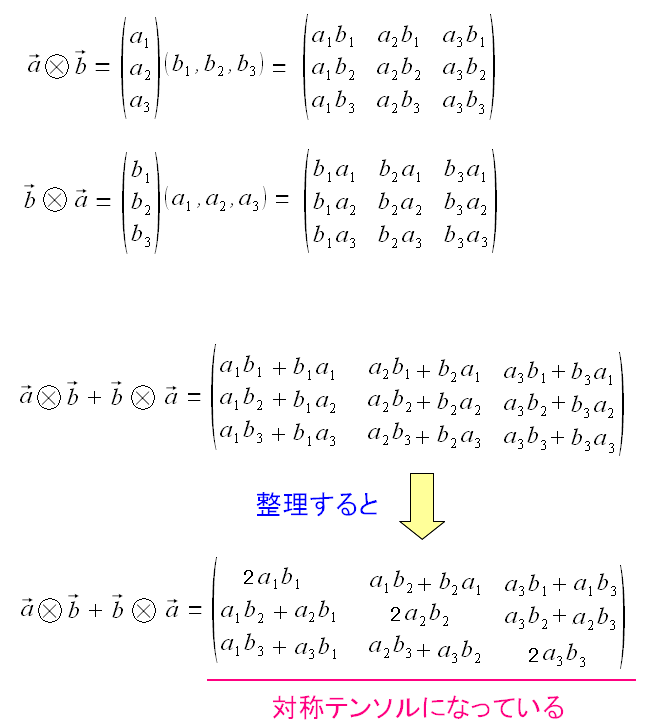上のように直積を計算すると対称行列になる。反対称行列の場合、差分を取るので、やっている事は反対の事なのだ。


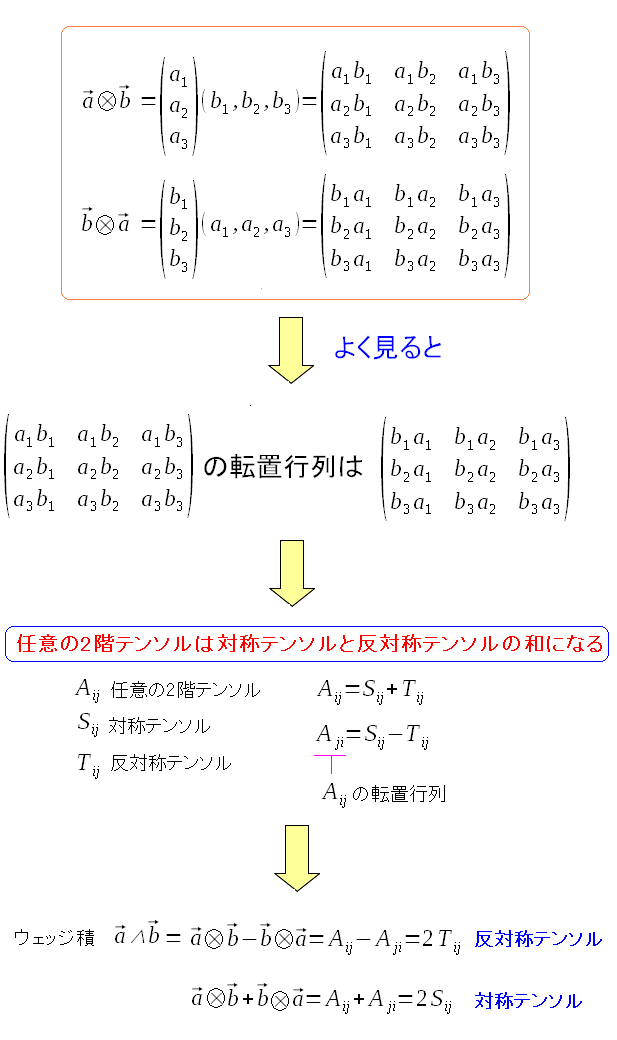
　2階の対称テンソルと2階の反対称テンソルとの間には次の法則がある。

2階の対称テンソルと2階の反対称テンソルとの間の法則

任意の2階のテンソルは、対称テンソルと反対称テンソルの和になるのだ。こんな事、考えた事もなかったのだ。


　ウェッジ積が2階のテンソルだとわかったし、ベクトルから作る方法も知った。
　そのため以下の特徴がある事が、計算によってわかるのだ。

ウェッジ積の特徴

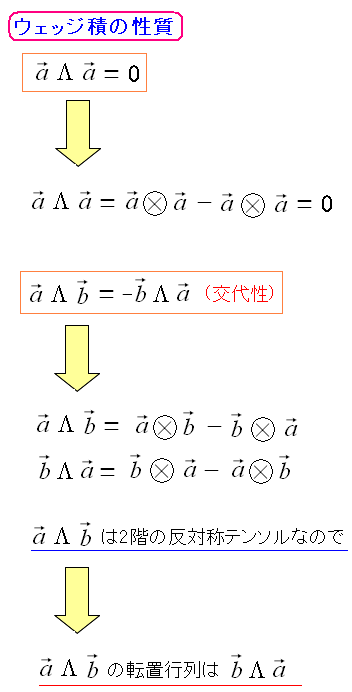同じベクトルの積はゼロになる。ベクトルの順序を交換して計算すると、元のウェッジ積の転置行列になるのだ。


　ウェッジ積についてはこれぐらいにして、次に、もう1つの外積で
線形代数で習うクロス積を見てみる。

外積というと
外積というと、線形代数ではクロス積の事を指す。だが、微分形式などを知ると、外積にはウェッジ積がある事も知る。そのためクロス積のつもりで外積といっても、相手に通じない場合があるので外積の呼び方には注意が必要になってくる。


　クロス積が何なのか。
　クロス積の定義を思い出して欲しい。ベクトルの積が、ベクトルになっている。

クロス積の定義

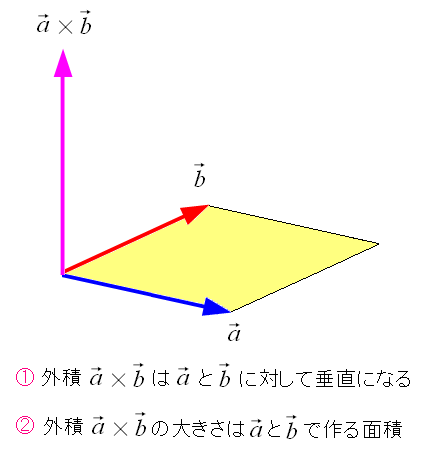2つのベクトルの積で作るベクトルなのだ。


　ところでウェッジ積は2階のテンソル(行列)だった。
　クロス積は2階のテンソルではなくベクトルなのか？

　そこでクロス積を詳しく見ていく事にする。

クロス積とはウェッジ積をベクトルにした物

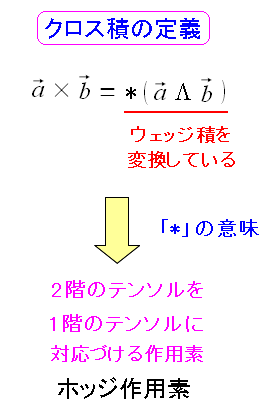クロス積とはウェッジ積(2階のテンソル)を1階のテンソル(ベクトル9にした物だ。


　どういう事なのか。
　ここでウェッジ積が反対称テンソルだった事を頭に入れながら、前に進んでみる。

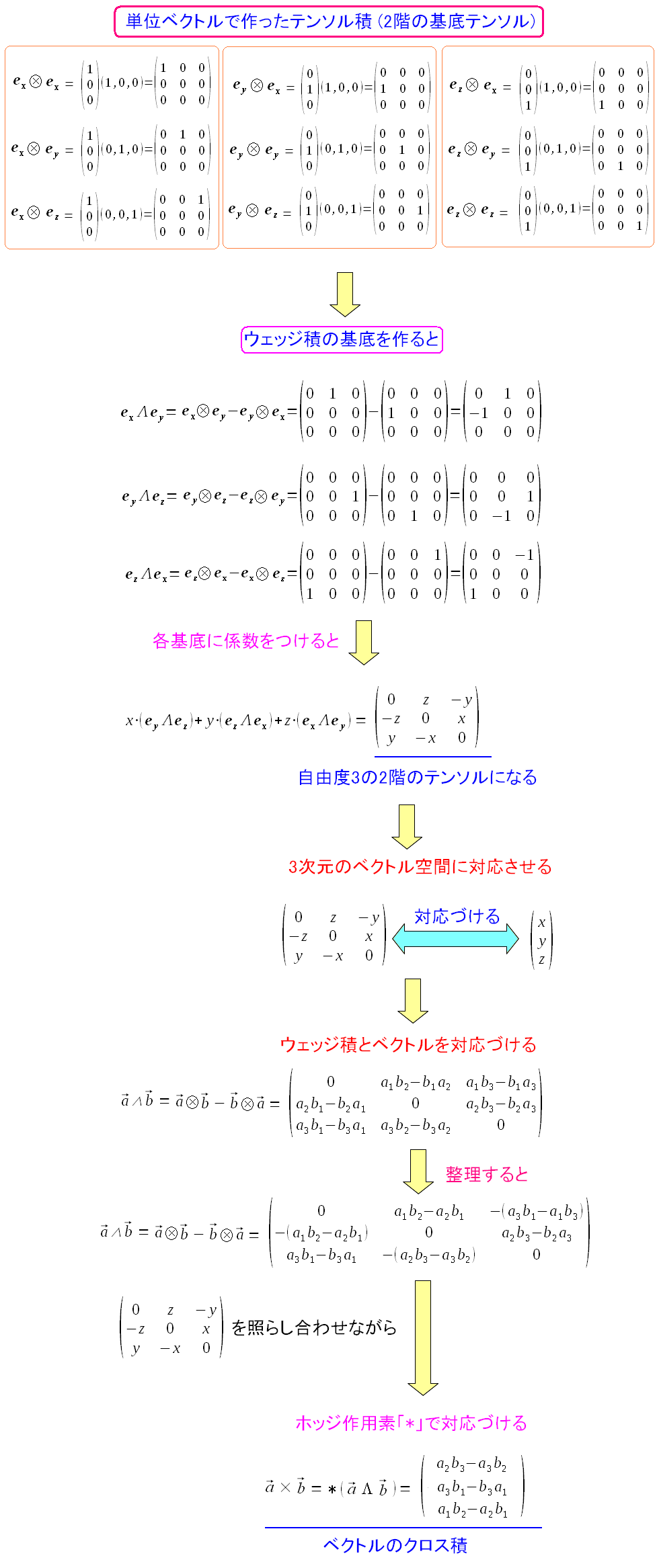
クロス積はベクトルとみなせる理由

ウェッジ積を求めた際、反対称テンソルになっている。しかも自由度が3のテンソルだ。3つしか独立した部分がない。これを3次元ベクトルと対応づける事がでくるのだ。


　クロス積は・・・

　みせかけのベクトル

　だったのだ。

　線形代数で習った外積(クロス積)の実体は2階のテンソルで
1階のテンソル(ベクトル)だったのは、あくまでも見せかけだったとは

　全く夢にも思わへんかった!!

　驚きとしか言いようがない。
　というよりも、学生時代、数学の勉強をしていなかったのが露呈された。
　でも・・・

　20年前なので笑い話なのらー!!

　クロス積の正体(?)がわかった所で、クロス積の計算規則をみていく。

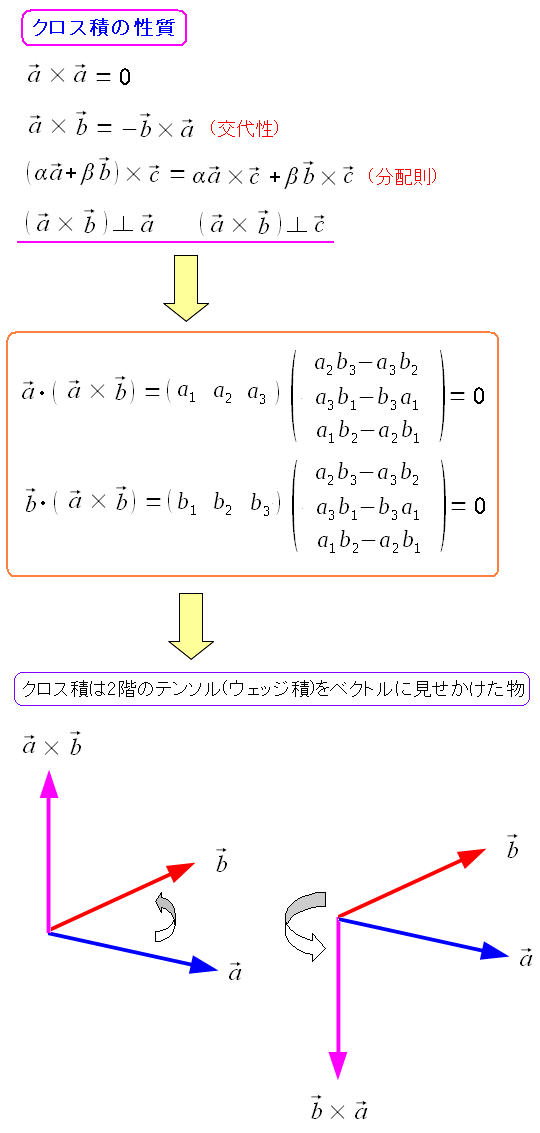
クロス積の計算規則

2つのベクトルのクロス積は、2つのベクトルに対して直交している。確認のため計算してみると、内積はゼロになる。見せかけのベクトルなのだが、クロス積の計算規則に従っている。


　クロス積は見せかけのベクトル。
　見せかけのベクトルだからこそ、他のベクトルとは違う振る舞いをするのだ。
　その振る舞いを見ていく事にする。


極性ベクトルと軸性ベクトル

　まずは準備として直交座標系でも2種類の座標系の説明をする。

右手系と左手系

　右手系と左手系なのだ。
　普段、我々が使っているのは、右手系の座標系なのだ。

　もちろん・・・

　左手系の座標系があったとは、知らへんかった!!

　どんどん数学力のなさを露呈していく私。

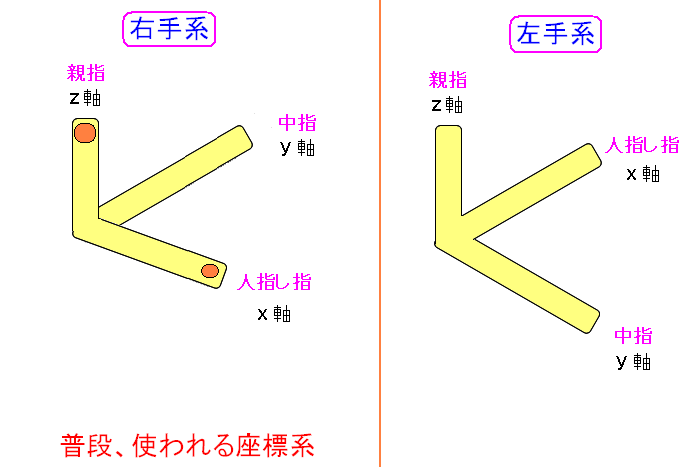
右手系と左手系

右手系と左手系では、X軸とY軸が入れ替わっている。右手と左手を使って表現すると、わかりやすいので、右手形・左手系というのだ。左手系の図。見ている視点では爪がみないように描いた。芸を細かくしているのだが、気づいてくれたかなぁ？(笑)


　手のモデルではなく、座標軸で見比べてみる。

右手系の座標軸と左手系の座標軸

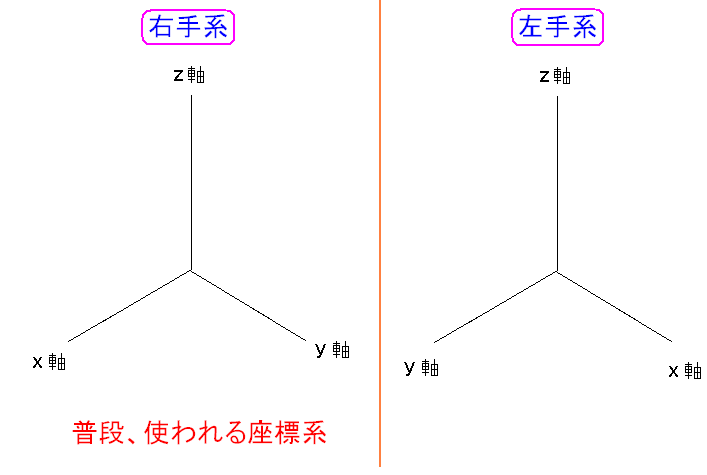右手系と左手系では、X軸とY軸が入れ替わっている。



　ところで右手系座標と左手系座標は2つの対象性が見られる。

　1つ目は

　軸対象

　になのだ。

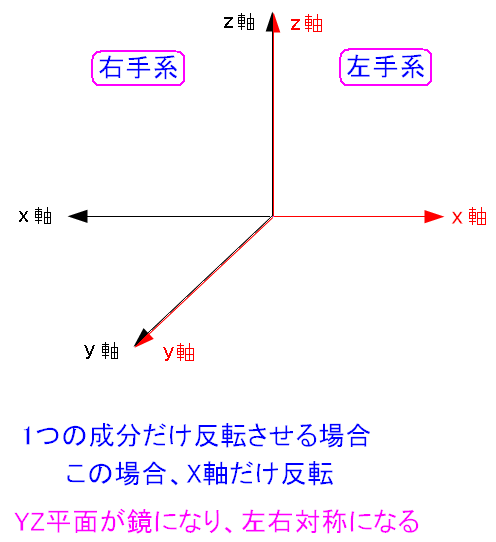
右手系座標と左手系座標は軸対象

軸対象になっている。軸対象は今回は使わないので触れないことにする。


　2つ目は

　原点対象

　になのだ。

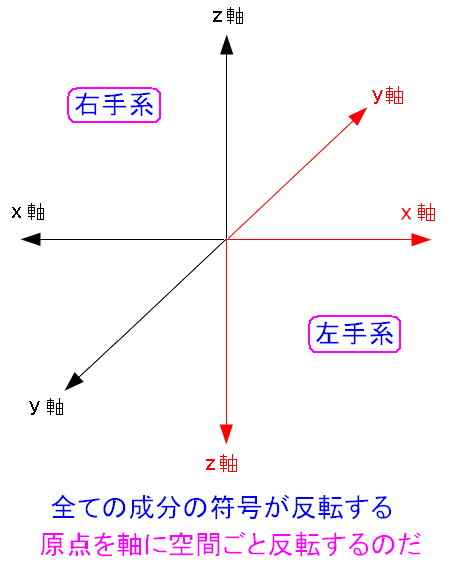
右手系座標と左手系座標は原点対象

原点で対称になっている。この原点対象がクロス積にとって大事な話につながる。


　ベクトルには2種類ある。

　極性ベクトルと軸性ベクトル

　なのだ。
　もちろん、2種類ある事なんて

　知るわけねぇーよ!

　なのだ。

　色々、調べた際、こんな区別を見つけた。

ネットで見つけた、極性ベクトルと軸性ベクトルの違い
その1	極性ベクトルは物理量のベクトルで軸性ベクトルは実体のない物理量。
その2	クロス積で求まったベクトルは軸性


　でも、この説明だとわかりにくいし、誤解を招きやすい。


　極性ベクトルと軸性ベクトルの違い。
　右手系座標と左手系座標を使えば、案外、わかりやすい。

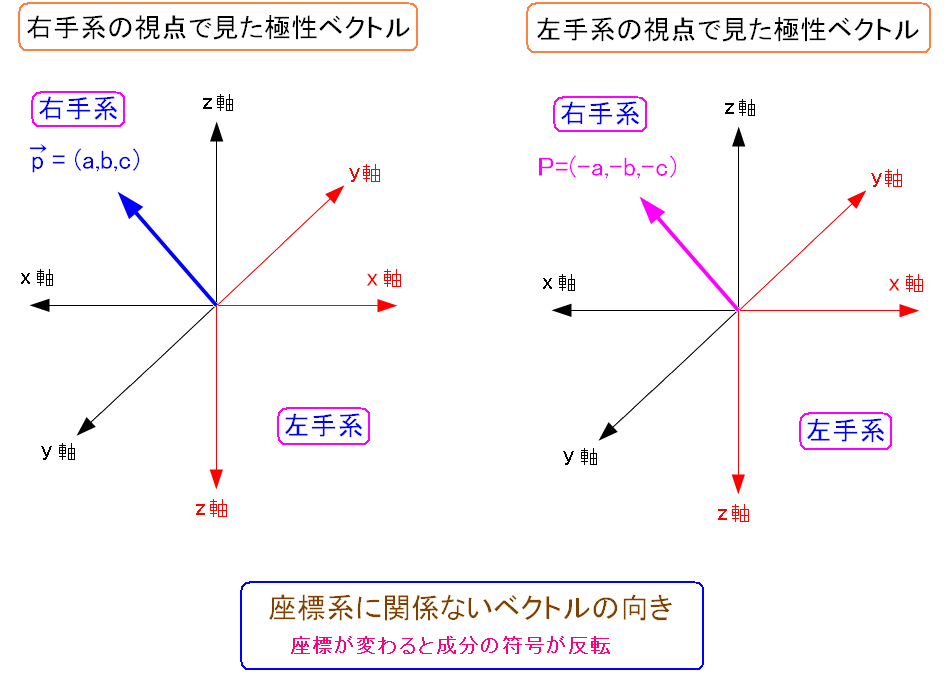
極性ベクトルと右手系座標と左手系座標

極性ベクトルは、座標形に関係なく向きは同じになる。そのため右手系と左手系では方向成分の符号が変わってしまうのだ。座標系に関係なく向きが同じなので、速度ベクトルや力の方向などが上げられる。


　次に軸性ベクトルを見てみる。

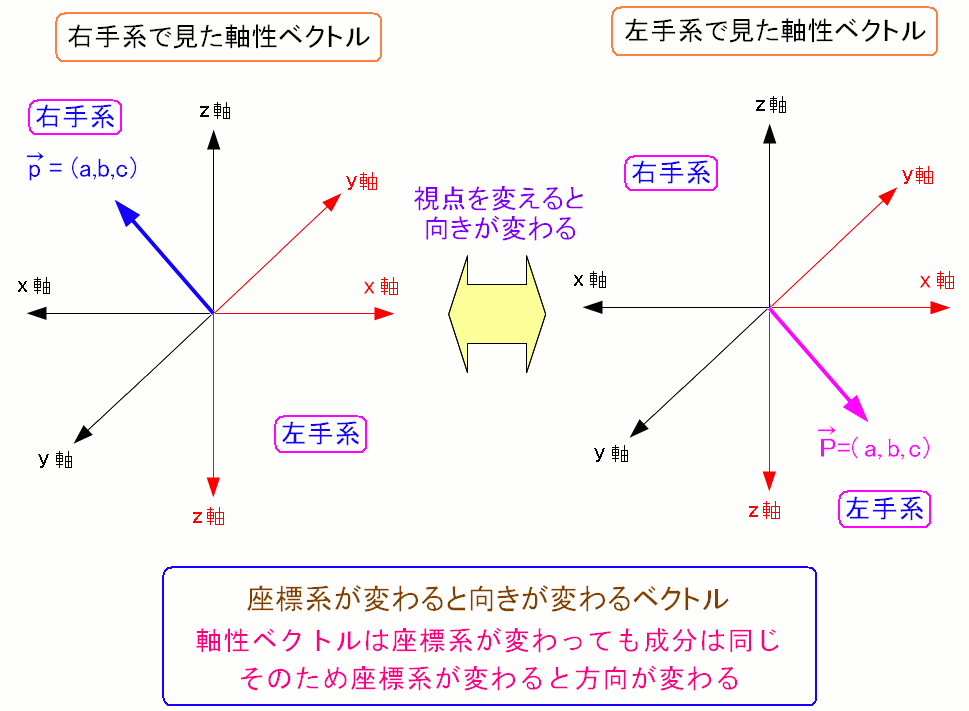
軸性ベクトルと右手系座標と左手系座標

軸性ベクトルとは座標系に関係なく方向成分が同じベクトルだ。そのため座標系が変わると向きが反対になるベクトルなのだ。


　軸性ベクトルの説明で、見せかけのベクトルと書いた。
　軸性ベクトルとは何やねんとなる。軸性ベクトルとは・・・

　2階のテンソルで

　実体のないベクトル

　なのだ。

　2階のテンソル(行列)がベクトルという、なんとも奇妙な話だ。

軸性ベクトルの正体は2階のテンソル

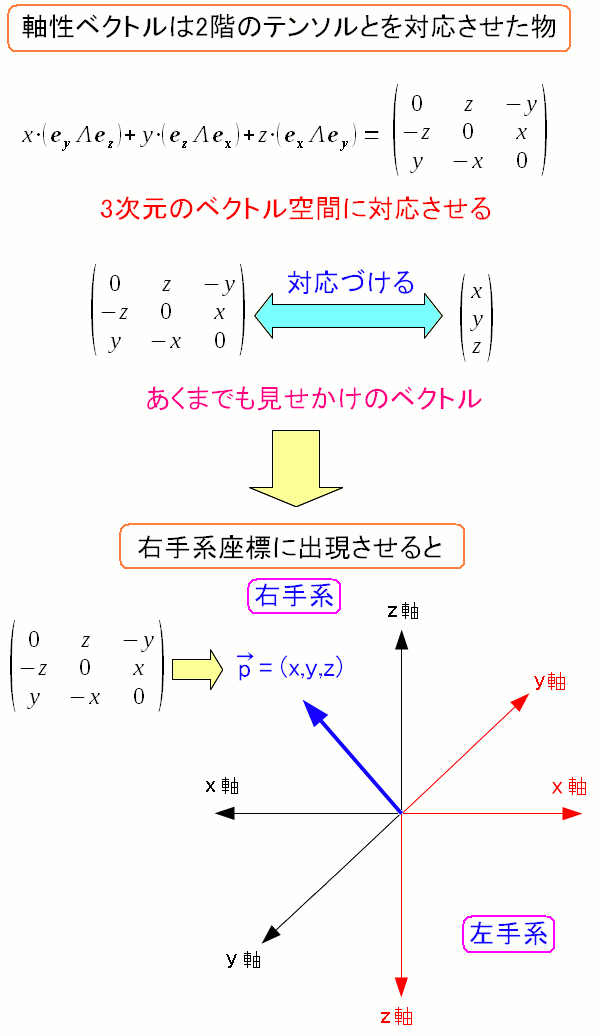2階のテンソルを右手系座標に出現させてみた。


　次に2階のテンソルを左手系座標に出現させてみる。

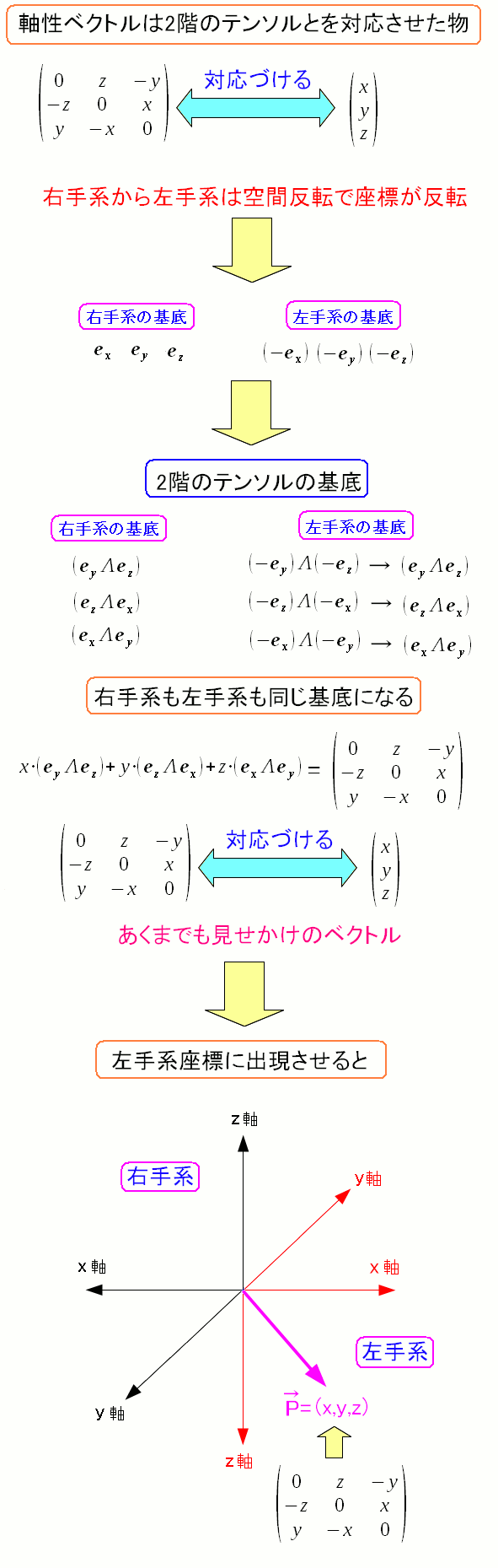
2階のテンソルを左手系座標に出現させてみた

左手系は、右手系の原点反転なので、基底ベクトルの向きが変わる。

右手系の場合と、左手系の場合の、それぞれの2階のテンソルの基底を求める。

すると2階のテンソルの基底が同じになってしまう。

2階のテンソルは空間反転しても成分は変わらないのだ。
なので軸性ベクトルは右手系でも左手形でも成分は同じなので
座標が変わると反対方向の向きになってしまうのだ。


　さて、2階のテンソルと対応させたベクトルが軸性ベクトルだとわかった。
　なのでクロス積でできたベクトルを軸性ベクトルと言いたくなるが

　クロス積でできた極性ベクトルもある

　のだ。

　本当にクロス積でできた極性ベクトルがあるのか、確かめてみる。

クロス積とベクトルの組み合わせ

2階のテンソルそのものは、極性ベクトルになる。
極性ベクトルと軸性ベクトルのクロス積が極性ベクトルになる。

なぜならクロス積の元になる2つのベクトルの組み合わせによって
2つの2階のテンソルができてしまうからだ。
そのためクロス積のベクトルが軸性ベクトルになるとは限らないのだ。


　調べていくと、磁場のベクトルは軸性ベクトルだと知った。
　軸性ベクトルは実体のない見せかけのベクトルなのだが

　どうして・・・

　磁場は軸性ベクトルやねん!

　という疑問が出てきた。

　物理量だし磁石の方向は決まっているので
磁場は極性ベクトルに思えるのだ。

　そこでビオ・サバールの法則を見直してみた。

ビオ・サバールの法則

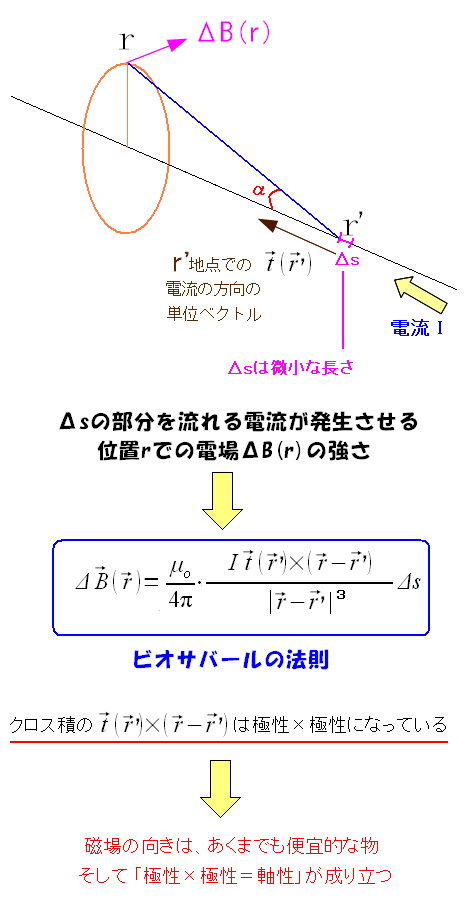極性ベクトル(電流の向き)と極性ベクトル(位置)のクロス積が磁場になっている。


　もしかして・・・

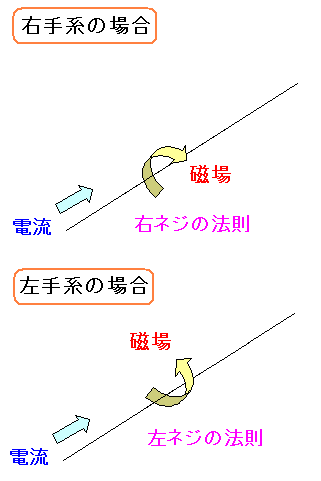
　右手系と左手系では磁場の向きが反転する

　という事になる。

右手系と左手系では磁場の向きが反転する

もしかして導線を流れる電流ができる磁場は座標系を変える事で、回転の方向が変わるためだ。


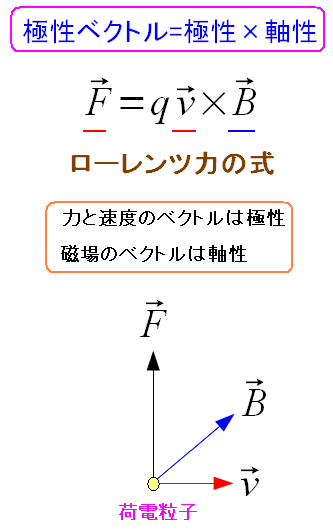
　わかったような、わからん説明。どうも解せない。

　磁場が軸性ベクトルである事が解せない。
　だが、磁場が軸性ベクトルなので、ローレンツ力が成り立つのだ。

磁場が軸性ベクトルなので、ローレンツ力が成り立つ

極性ベクトルと軸性ベクトルのクロス積は、極性ベクトルになる。その具体例がローレンツ力で出てくるクロス積なのだ。


　数式を見て磁場が軸性ベクトルなのは明らかなのだが
それを納得するのは、案外、難しい。

　でも、大学生が頭を悩ませているのは仕方がない。
　彼らは極性ベクトルと軸性ベクトルの違いを知って悩んでいる。

　私のように学生時代、2つのベクトルの存在すら

　知らんかったため、悩まんかった

　のだ。悩める学生は勉強しているなぁと改めて思った。


電磁気学入門の目次

電磁気学入門:目次
スカラーとベクトル	簡単なスカラーとベクトルの話です。ベクトルは方向と大きさを持つ量。方向という量持っているだけに注意が必要です。
静電気の発見からクーロンの法則	今でこそ当たり前の静電気や導体、絶縁体、電荷などどういう経緯で発見し、クーロンの法則まで至ったのかの話です。
クーロン力、電場、近接作用	4つの力のうち、クーロン力の位置づけ電荷が作り出す作用の電場。近接作用の話です。
微分、全微分、方向微分	簡単な微分、全微分、方向微分の話です。ここをしっかり押さえないと、電磁気の数式の意味がわからなくなります。
ベクトル解析	電磁気に必要なベクトル解析の話です。勾配(grad)、2次元のグリーン定理ストークスの定理の話です。
電位ポテンシャル	電位ポテンシャルです。勾配と電場の関係を使って説明しています。
電気双極子	電気双極子の話です。物質中で起こる分極を理解するのに必要です。
ガウスの法則	ガウスの法則の積分形、微分形の話です。
ポアソンの方程式、ラプラス方程式	ポアソンの方程式、ラプラス方程式の話です。単に電荷分布から電位を求めるだけの話にとどまらない奥が深い分野です。ポテンシャル論、デルタ関数グリーン関数、固有値問題について触れています。
静電場と渦なしの法則	静電場で、電荷を1周させた時の仕事はゼロ微分形と微分形の渦なしの法則の話です。
ビオサバールの法則	電気と磁場の関係の発見の話からビオ・サバールの法則が導かれるまでの話です。
磁気双極子	磁気双極子の話で、回転電流になります。物質中の磁場の話にも関連します。
アンペールの法則	アンペールの法則の話です。積分形・微分形だけでなく、閉回路に流れる電流が作る磁気双極子の話なども書いています。
ローレンツ力	磁場中を移動する電荷にかかる力(ローレンツ力)の話です。ローレンツ力は相対性理論が絡んでいる事も紹介しています。
ファラデーの誘導起電力の法則	ファラデーの誘導起電力の話です。
うず電流を使った簡単な物理実験	電力計に使われるアラゴの円盤。そしてIH調理器で熱するために発生させる、うず電流はレンツの法則から電流が発生する原理を応用した物だ。アラゴの円盤の実験と、IH調理器を使った実験です。気分転換で読んでください。
ベクトルポテンシャル	わかりにくいベクトルポテンシャルの話です。電位は電荷が作る電気のポテンシャルだがベクトルポテンシャルは電流が作る磁場のポテンシャルの話です。
オームの法則の微分形	微小領域でのオームの法則の話です。
マックスウェルの方程式	4つのマックスウェルの方程式を書いています。電場と磁場の変化を図にする事で rotの回転の意味も理解できます。
ゲージ変換	ゲージ(gauge)は物差しの意味です。マックスウェルの方程式をE（電場）とB(磁場)の関係式から φ(電位ポテンシャル)とA(ベクトルポテンシャル)の関係式に書き換える際、ゲージ変換が使われます。ゲージ変換の役目を書きました。
電磁波	マックスウェルの方程式から電波が伝わる様子を視覚的に見てみる話です。
回転のrotはベクトルの微分	ベクトル解析や渦なしの法則で出てくるrotはベクトルの微分という話です。
電磁気学の単位系	電磁気学の単位系の話です。物理量の単位系の指数を見る次元解析電磁気学の歴史と単位系の変遷について触れました。
電気泥棒:電気と法律の話	電気は物体なのか、無形物なのか。明治時代に、電気を無断で使った場合、物か、そうでないかで窃盗罪になるかどうかが裁判で問われました。ちょっとした科学と法律の話です。気分転換で読んでください。
数ベクトルと基底ベクトル	ベクトルの話です。矢印だけがベクトルでない事。数ベクトルと基底ベクトルの違いの話です。多様体、反変・共変ベクトルを理解するのに必要です
多様体	空間を一般化した話です。 ▽(ナブラ)の正体に迫まります
外積代数	外積、テンソルについて書いています。極性ベクトル、軸性ベクトル外積は行列で、ベクトルは見せかけの姿だった話です。
ベクトルの双対関係	反変ベクトル、共変ベクトル、双対関係ベクトル解析、外積代数の話外積、テンソルについて書いています。
ローレンツ力と相対性理論	磁場は電場の相対論的効果だった話です。ローレンツ力を使って、導線が作る磁場を使って説明です。
微分形式	多様体の話の続きです。座標に依存しない形での関数やベクトルの微分の話です。ガウスの法則、アンペールの法則、マックスウェルの方程式が鮮やかな形で表現できます。 ∇(ナブラ)の正体もわかります。
物理と対称性	マックスウェルの方程式をよく見ると対称性があります。物理の方程式と対称性を数学的な観点でみると意外なつながりがあるという話です。
マックスウェルの応力	電気力線を弾性体(ゴム)とみなして、力の伝わり方などを説明した考え方です。
電場エネルギー	電場が持つエネルギーの式を導いた話です。
磁場エネルギー	磁場が持つエネルギーの式です。手抜きの説明と、直流RL回路を使った説明を書きました。
ポインティングベクトル	電磁エネルギーの流れ「ポインティングベクトル」の話です。電磁波でもエネルギー保存則が成り立つ話からポインティングベクトルを導いています。
電気エネルギーは導線の外を伝わる	導線の外を電気エネルギーが流れる話です。私が誤解した事、その誤解を解いていく過程を紹介しながら「目からウロコ」にたどり着いた話です。
物質中の電場	物質中の電場の話です。分極の話をしながら、物質中の電場の話をします
物質中の磁場	磁性の話をしながら、物質中の磁場の話をします
物質中のマックスウェルの方程式	物質中でもマックスウェルの方程式が成り立つ話です。
導体に侵入する電磁波	導体に侵入する電磁波が減衰していく話です。表皮効果と同じ「表皮の厚さ」が出てきます
表皮効果	目的の表皮効果の話です。マックスウェルの方程式を解きながら交流電流の周波数を上げると、表面にしか電流が流れなくなる話です。

電磁気学の目次:「電磁気学入門」に戻る

前章:「無線LANの基礎無線LAN入門と導入事例」を読む
システム奮闘記の目次:システム奮闘記に戻る