システム奮闘記:その105
(2016年5月22日に掲載)
磁場のポテンシャル
ベクトルポテンシャル。 よくわからん存在なのだ。本を見てもわからない。 もちろん学生時代に電磁気学の所で習ったが 全く理解できへんかった!! そもそも B=▽×Aと置いて、何を意味するねん!! だった。 私が学生時代、インターネット上で、大学の講義資料の公開なんてなかったし わかりやすいサイトもなかった。 だが、21世紀になって15年も経つと探せば見つかるのだ。 琉球大学の前野昌弘さんが作成された講義資料を発見した。 2008年度電磁気学II 講義録(PDF) 琉球大学の電磁気学2013年度講義資料 前野さんの資料を見た時 目からウロコ だったのだ。 その感激を伝えたくなったので、ベクトルポテンシャルについても触れる事にした。
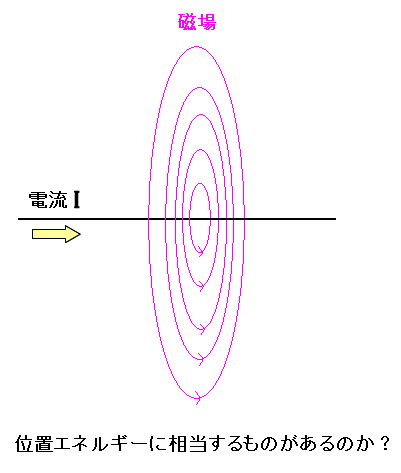
| 磁場にポテンシャルのはあるのか? |
|---|
 |
先人が、そういう風に考えるもの不思議ではない。
| 電場のようには、うまくいかない |
|---|
 |
|
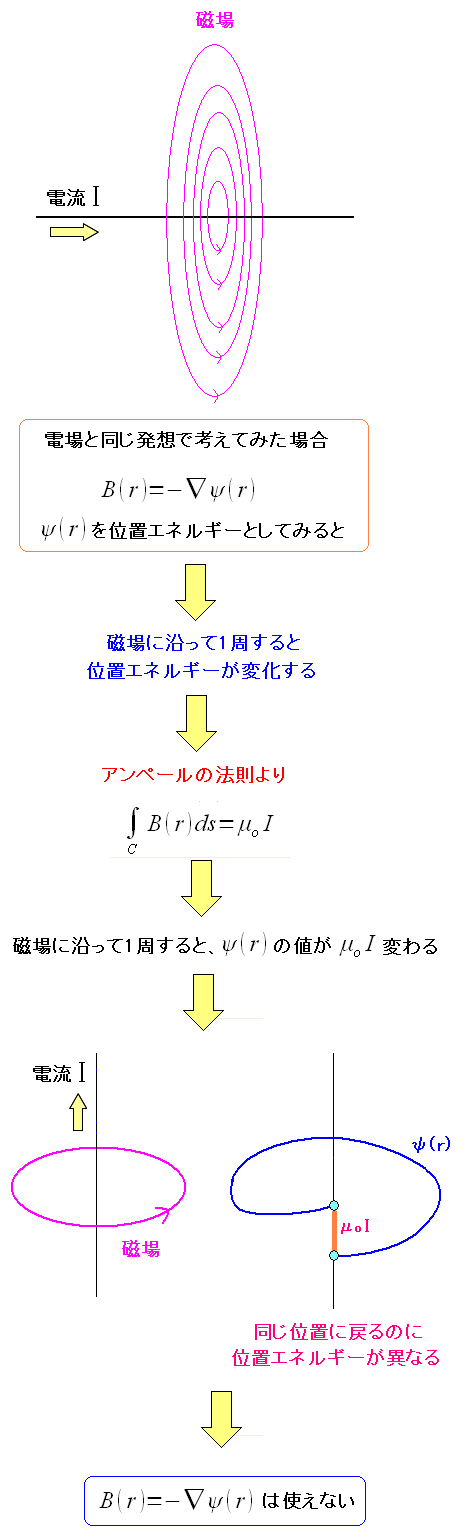
だが、磁場の場合、導線の周囲を回るため 電場と同じ定義でポテンシャルを決めると問題点が出てくる。 階段を登り降りして元の位置に戻ったら、1階から2階に 上がっていたという感じになるのだ。 |
でも、これでめげない先人達だった。
| 渦無しの法則を活用する |
|---|
 |
|
ベクトルAは、ベクトルポテンシャルと定義する。 この時、「B=▽×A」の定義式が出てくるのだ。 ∇・B=0なので、B=▽×AとなるベクトルAが存在する。 任意のベクトルAは、∇・(▽×A)=0になる だいぶ後で紹介する微分形式をすれば、すっきりした形で 納得できるのだ。それはお楽しみに。 |
だが、この段階では 「B=▽×A」だから何やねん? になる。
電流が作る位置エネルギー
「B=▽×A」なのだが、これを絵に描いてみると、わかりやすくなる。
| 「B=▽×A」を絵にしてみる |
|---|
 |
|
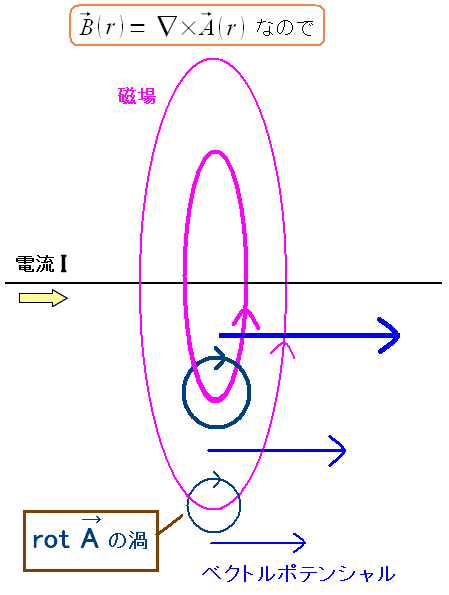
磁場は導線から遠ざかれば遠ざかる程、弱くなる。 それと磁場は、導線の周囲を円形状のように回転している。 内側の磁場と外側の磁場との間には強さの差が生じる。 この時に発生している渦こそ、ベクトルポテンシャルの渦になる。 |
そして前野さんの講義資料に ベクトルポテンシャルは電流が作る位置エネルギー という文字を見た。 思わず目からウロコ
| ベクトルポテンシャルは電流が作る位置エネルギー |
|---|
 |
|
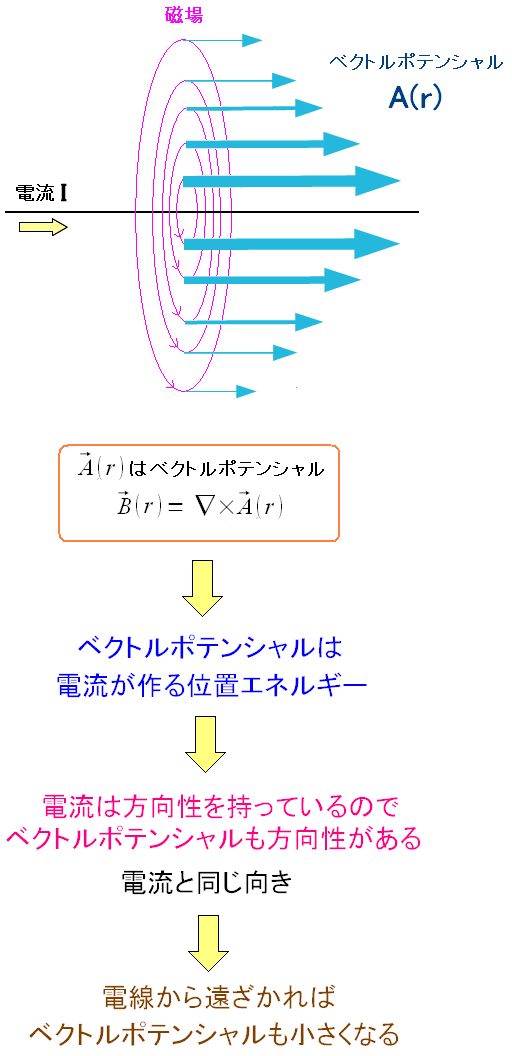
電流の向きと並行の方向にあるベクトルポテンシャル。 導線から遠ざかると、強さが減っていくのだ。 これだとベクトルポテンシャルが導線から遠ざかると 磁場(B=▽×A)も小さくなる事が納得できる。 |
そして ベクトルポテンシャルが電流と同じ向きとは 想像もしてへんかった!!! のだ。 ところで電場では、電位から点電荷の分布を知る事ができる。 同じように、ベクトルポテンシャルでも、同じような物があるのか。
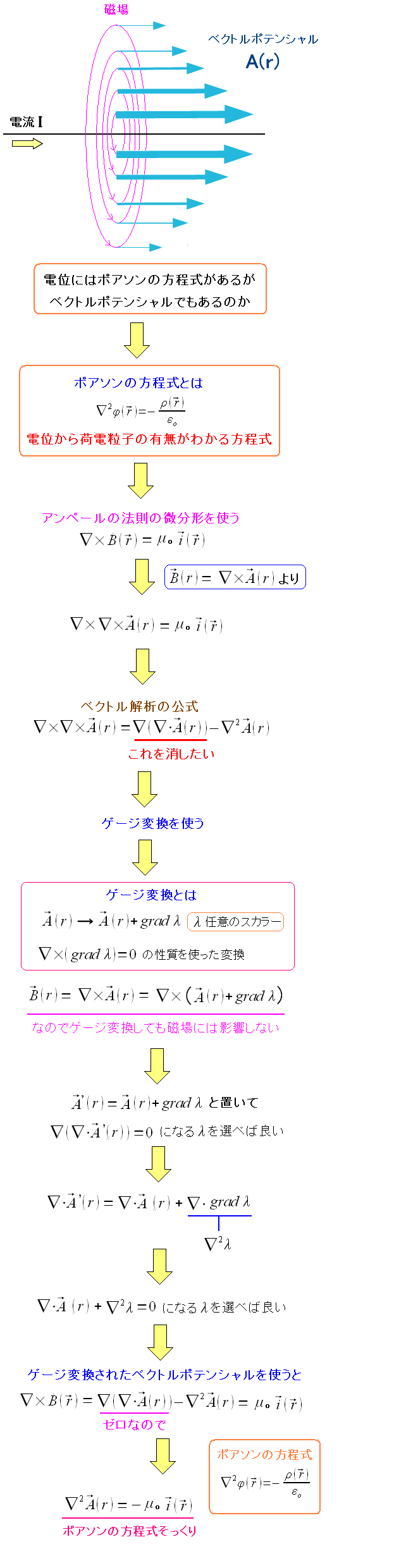
| 磁場では、ポアソンの法則に相当するのがあるのか |
|---|
 |
|
アンペールの法則の微分形を活用すれば、導き出せるという。 その結果、ポアソンの方程式にそっくりな物が導ける。 電位ポテンシャルの場合、ポアソンの方程式により その空間の荷電粒子の密度がわかる。 ベクトルポテンシャルの場合、導線を流れる電流密度がわかるのだ。 |
ところでゲージ変換の所は軽く流した。 そのため読者から ゲージ変換は取り上げへんのか? と言われそうだ。 逃げようと思ったのだが、逃げられそうにもないので ゲージ変換の章を設けて、少し触れる事にした。 ただ、マックスウェルの方程式の話を知らないと、 ゲージ変換の話が理解できない(少なくとも私は理解できなかった)ので マックスウェルの方程式の話の後に、ゲージ変換について書きました。
電磁気学入門の目次
| 電磁気学入門:目次 | |
|---|---|
| スカラーとベクトル | 簡単なスカラーとベクトルの話です。 ベクトルは方向と大きさを持つ量。方向という量持っているだけに注意が必要です。 |
| 静電気の発見からクーロンの法則 | 今でこそ当たり前の静電気や導体、絶縁体、電荷など どういう経緯で発見し、クーロンの法則まで至ったのかの話です。 |
| クーロン力、電場、近接作用 | 4つの力のうち、クーロン力の位置づけ 電荷が作り出す作用の電場。近接作用の話です。 |
| 微分、全微分、方向微分 | 簡単な微分、全微分、方向微分の話です。 ここをしっかり押さえないと、電磁気の数式の意味が わからなくなります。 |
| ベクトル解析 |
電磁気に必要なベクトル解析の話です。 勾配(grad)、2次元のグリーン定理 ストークスの定理の話です。 |
| 電位ポテンシャル | 電位ポテンシャルです。勾配と電場の関係を使って説明しています。 |
| 電気双極子 |
電気双極子の話です。 物質中で起こる分極を理解するのに必要です。 |
| ガウスの法則 | ガウスの法則の積分形、微分形の話です。 |
| ポアソンの方程式、ラプラス方程式 |
ポアソンの方程式、ラプラス方程式の話です。 単に電荷分布から電位を求めるだけの話にとどまらない 奥が深い分野です。ポテンシャル論、デルタ関数 グリーン関数、固有値問題について触れています。 |
| 静電場と渦なしの法則 |
静電場で、電荷を1周させた時の仕事はゼロ 微分形と微分形の渦なしの法則の話です。 |
| ビオサバールの法則 |
電気と磁場の関係の発見の話から ビオ・サバールの法則が導かれるまでの話です。 |
| 磁気双極子 |
磁気双極子の話で、回転電流になります。 物質中の磁場の話にも関連します。 |
| アンペールの法則 |
アンペールの法則の話です。 積分形・微分形だけでなく、閉回路に流れる電流が作る 磁気双極子の話なども書いています。 |
| ローレンツ力 |
磁場中を移動する電荷にかかる力(ローレンツ力)の話です。 ローレンツ力は相対性理論が絡んでいる事も紹介しています。 |
| ファラデーの誘導起電力の法則 | ファラデーの誘導起電力の話です。 |
| うず電流を使った簡単な物理実験 | 電力計に使われるアラゴの円盤。 そしてIH調理器で熱するために発生させる、うず電流は レンツの法則から電流が発生する原理を応用した物だ。 アラゴの円盤の実験と、IH調理器を使った実験です。 気分転換で読んでください。 |
| ベクトルポテンシャル |
わかりにくいベクトルポテンシャルの話です。 電位は電荷が作る電気のポテンシャルだが ベクトルポテンシャルは電流が作る磁場のポテンシャルの話です。 |
| オームの法則の微分形 | 微小領域でのオームの法則の話です。 |
| マックスウェルの方程式 |
4つのマックスウェルの方程式を書いています。 電場と磁場の変化を図にする事で rotの回転の意味も理解できます。 |
| ゲージ変換 |
ゲージ(gauge)は物差しの意味です。 マックスウェルの方程式をE(電場)とB(磁場)の関係式から φ(電位ポテンシャル)とA(ベクトルポテンシャル)の関係式に 書き換える際、ゲージ変換が使われます。 ゲージ変換の役目を書きました。 |
| 電磁波 |
マックスウェルの方程式から電波が伝わる様子を 視覚的に見てみる話です。 |
| 回転のrotはベクトルの微分 |
ベクトル解析や渦なしの法則で出てくるrotは ベクトルの微分という話です。 |
| 電磁気学の単位系 | 電磁気学の単位系の話です。 物理量の単位系の指数を見る次元解析 電磁気学の歴史と単位系の変遷について触れました。 |
| 電気泥棒:電気と法律の話 |
電気は物体なのか、無形物なのか。 明治時代に、電気を無断で使った場合、物か、そうでないかで 窃盗罪になるかどうかが裁判で問われました。 ちょっとした科学と法律の話です。気分転換で読んでください。 |
| 数ベクトルと基底ベクトル | ベクトルの話です。 矢印だけがベクトルでない事。 数ベクトルと基底ベクトルの違いの話です。 多様体、反変・共変ベクトルを理解するのに必要です |
| 多様体 | 空間を一般化した話です。 ▽(ナブラ)の正体に迫まります |
| 外積代数 |
外積、テンソルについて書いています。 極性ベクトル、軸性ベクトル 外積は行列で、ベクトルは見せかけの姿だった話です。 |
| ベクトルの双対関係 |
反変ベクトル、共変ベクトル、双対関係 ベクトル解析、外積代数の話 外積、テンソルについて書いています。 |
| ローレンツ力と相対性理論 |
磁場は電場の相対論的効果だった話です。 ローレンツ力を使って、導線が作る磁場を使って説明です。 |
| 微分形式 |
多様体の話の続きです。 座標に依存しない形での関数やベクトルの微分の話です。 ガウスの法則、アンペールの法則、マックスウェルの方程式が 鮮やかな形で表現できます。 ∇(ナブラ)の正体もわかります。 |
| 物理と対称性 |
マックスウェルの方程式をよく見ると対称性があります。 物理の方程式と対称性を数学的な観点でみると 意外なつながりがあるという話です。 |
| マックスウェルの応力 |
電気力線を弾性体(ゴム)とみなして、力の伝わり方などを 説明した考え方です。 |
| 電場エネルギー | 電場が持つエネルギーの式を導いた話です。 |
| 磁場エネルギー |
磁場が持つエネルギーの式です。 手抜きの説明と、直流RL回路を使った説明を書きました。 |
| ポインティングベクトル |
電磁エネルギーの流れ「ポインティングベクトル」の話です。 電磁波でもエネルギー保存則が成り立つ話から ポインティングベクトルを導いています。 |
| 電気エネルギーは導線の外を伝わる |
導線の外を電気エネルギーが流れる話です。 私が誤解した事、その誤解を解いていく過程を紹介しながら 「目からウロコ」にたどり着いた話です。 |
| 物質中の電場 | 物質中の電場の話です。 分極の話をしながら、物質中の電場の話をします |
| 物質中の磁場 | 磁性の話をしながら、物質中の磁場の話をします |
| 物質中のマックスウェルの方程式 | 物質中でもマックスウェルの方程式が成り立つ話です。 |
| 導体に侵入する電磁波 |
導体に侵入する電磁波が減衰していく話です。 表皮効果と同じ「表皮の厚さ」が出てきます |
| 表皮効果 |
目的の表皮効果の話です。 マックスウェルの方程式を解きながら 交流電流の周波数を上げると、表面にしか電流が流れなくなる話です。 |