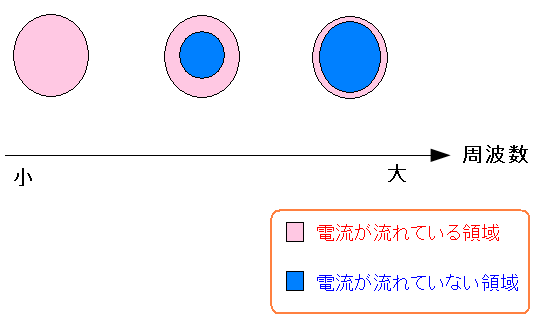
導線の中心部分が電流が流れなくなる。
周波数を上げていけばいくほど、電流が流れない領域が広がり
最後には導線の表面しか電流が流れなくなる現象だ。
システム奮闘記:その105
(2016年5月22日に掲載)
表皮効果
なんとか最終目的である、表皮効果を知るための準備ができたのだ。
| 表皮効果とは |
|---|
 |
|
導線を使って交流電流を流す際、周波数を高くするにつれ 導線の中心部分が電流が流れなくなる。 周波数を上げていけばいくほど、電流が流れない領域が広がり 最後には導線の表面しか電流が流れなくなる現象だ。 |
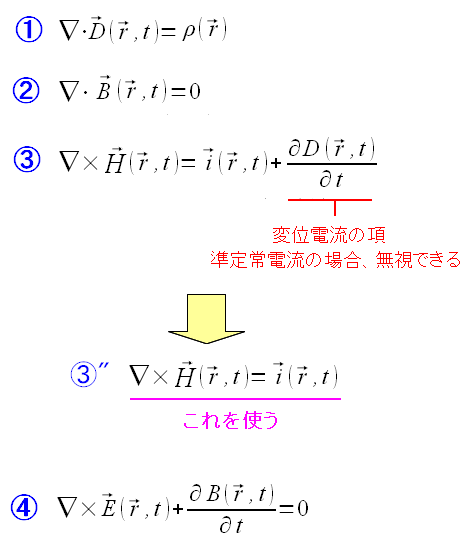
電線に交流電流を流す際、表面に電流が偏る事で、電気抵抗が上がり、 結果的に電流が流れにくくなるのだ。 高周波信号も交流電流と同じなので、導線中に高周波信号を流すと 電気抵抗が上がるため、信号が減衰しやすくなるのだ。 ところで導線の中は物質なので、物質中のマックスウェルの方程式が成り立つ。
| 物質中のマックスウェルの方程式 |
|---|
 |
|
LANケーブルの中を通る信号が高周波といっても 変位電流の影響は無視できるぐらい小さいのだ。 |
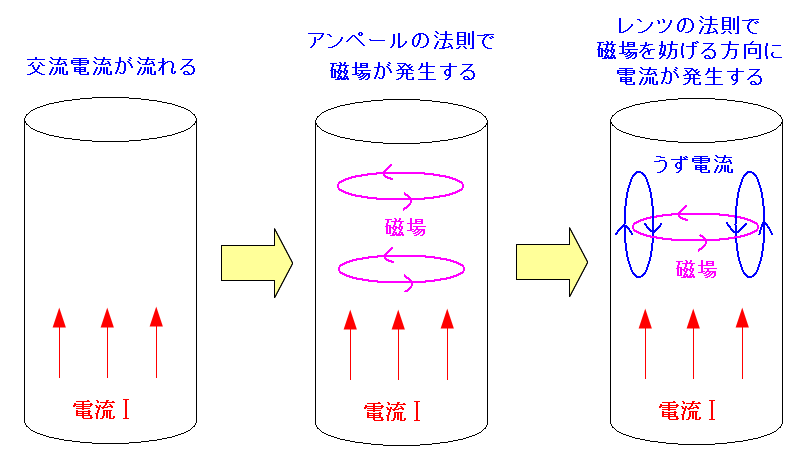
まずは定性的な話から見ていく事にする。 案外、表皮効果の原理を説明したサイトがなかったりする。 でも、Wikipediaの英語版は、詳しく書いていた。 Skin effect(表皮効果のWikipediaの英語版) Wikipediaに書いている事を丸写しに近い形で、交流電流が導線内を流れた時、 どういう現象が起こっているのか、図にしてみた。
| 表皮効果の原理(交流電流が流れると) |
|---|
 |
|
交流電流の場合、プラスとマイナスが交互になる。 プラスになって電流が流れはじめるとする。 電流が流れ始めた事により、電流の周囲に磁場が発生する。 アンペールの法則より。 磁場が急に発生するため、磁場の発生を抑制する方向に うず電流が発生するのだ。レンツの法則 |
うず電流。中心部は交流電流と反対の向きになっている。
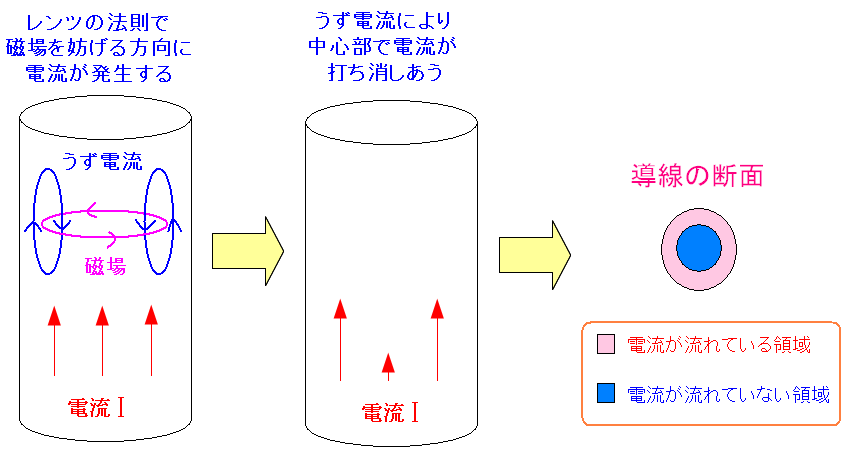
| 表皮効果の原理(うず電流が発生すると) |
|---|
 |
|
うず電流が中心部の電流を打ち消してしまうため 中心部には電流が流れなくなるという事なのだ。 周波数を高くすれば、磁場の変化が激しくなり その分、うず電流の電流量も増え、打ち消す度合いが大きくなるのだ。 |
そして、Wikipediaの内容を見て驚いた。
何も高周波信号の減衰だけが問題ではないようだ。
60Hzの交流を銅線を流した場合、表面から8.5mmの深さまでしか電流が流れないという。
大量の電気を流すため太い銅線を使っても意味あらへん
というのだ。
案外、身近な送電でも問題になっているのだ。知らなかった。
表皮効果は、1887年にウィリアム・トムソン(ケルビン卿)によって発見されたという。
案外、古くから知られた問題なのだ。
表皮効果よりも、絶対温度の発見などで有名なので、絶対温度は
彼の名前からとって「ケルビン」と名づけられたのだ。
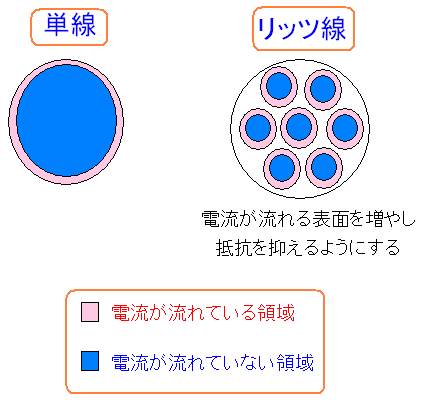
表皮効果の対策としてリッツ線(Litz Wire)が使われている。
| リッツ線 |
|---|
 |
|
1本の導線で作った線を単線という。 これだと表皮効果のため、内部では電流が流れなくなる。 そこで小さな導線を束ねる事により、電流が流れる表面を増やして 抵抗を減らすというのだ。 |
導線内は、表皮効果だけでなく近接効果もあるのだが 今回は、表皮効果にだけ話を絞るため、別の機会に説明します。
マックスウェルの方程式から求める表皮効果
定性的な話は、なんとなくわかった所で、マックスウェルの方程式に基づいて 表皮効果を計算する事にした。
| 物質中のマックスウェルの方程式 |
|---|
 |
|
LANケーブルの中を通る信号が高周波といっても 変位電流の影響は無視できるぐらい小さいのだ。 |
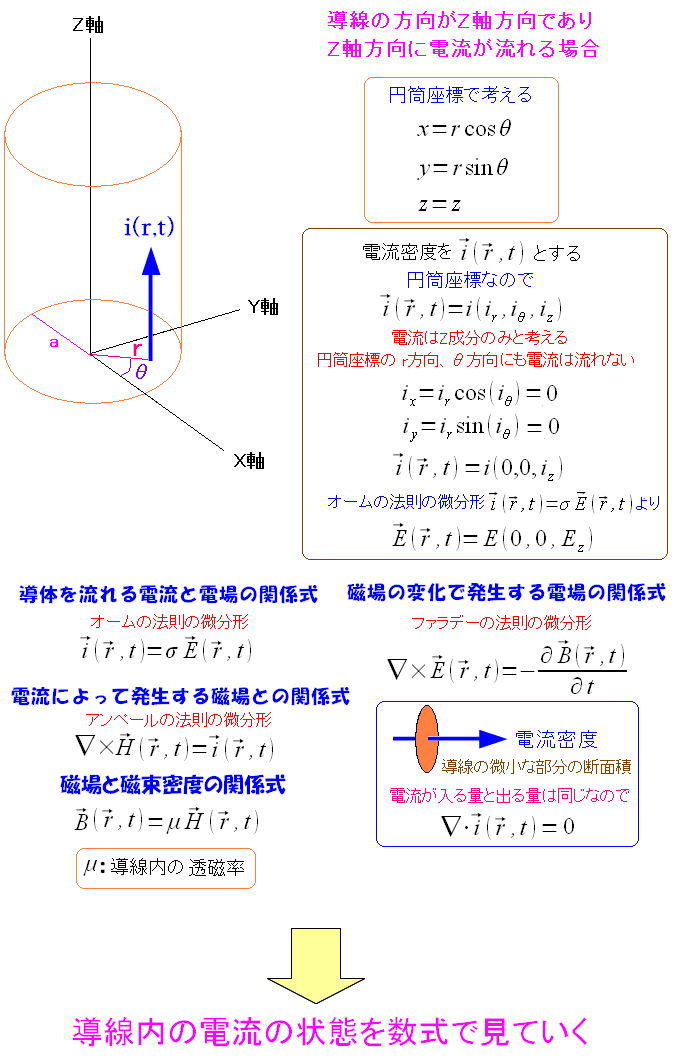
この式を使って、表皮効果という物理現象を見ていくのだ。 問題を簡単にするため、導線をZ軸を中心とする円筒形とする。
| 導線を原点中心とする円筒形とする |
|---|
 |
|
導線内の個々の物理現象(マックスウェルの方程式など)がある。 この式を使って、導線内の電流密度、磁場、電場を求めてみるのだ。 |
まずは導線内の電場の方程式を求めてみる。
| 導線内の電場の方程式 |
|---|
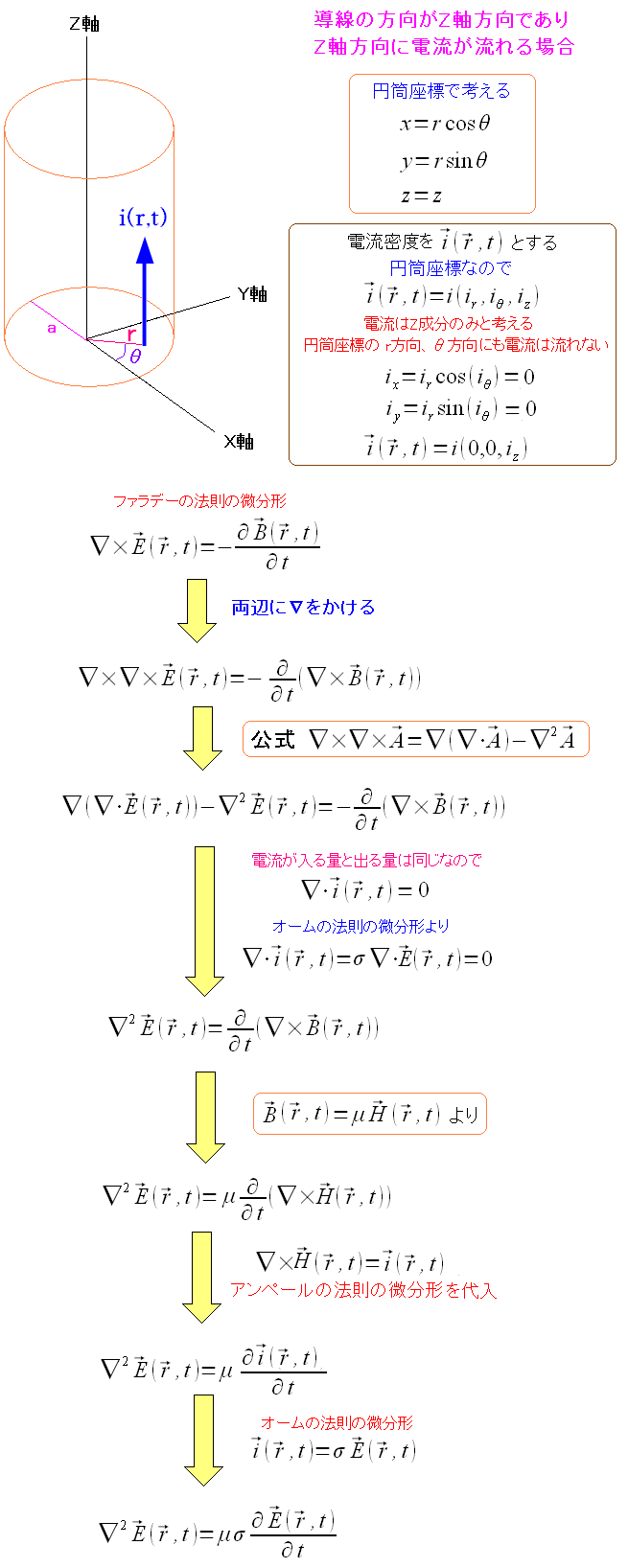 |
|
なぜ、最初の所で∇をかけるのかは、計算技術としか言いようがない。 でも、電場の微分方程式が求まったのだ。 |
次に導線内の磁場の方程式を求める。
| 導線内の磁場の方程式を求める |
|---|
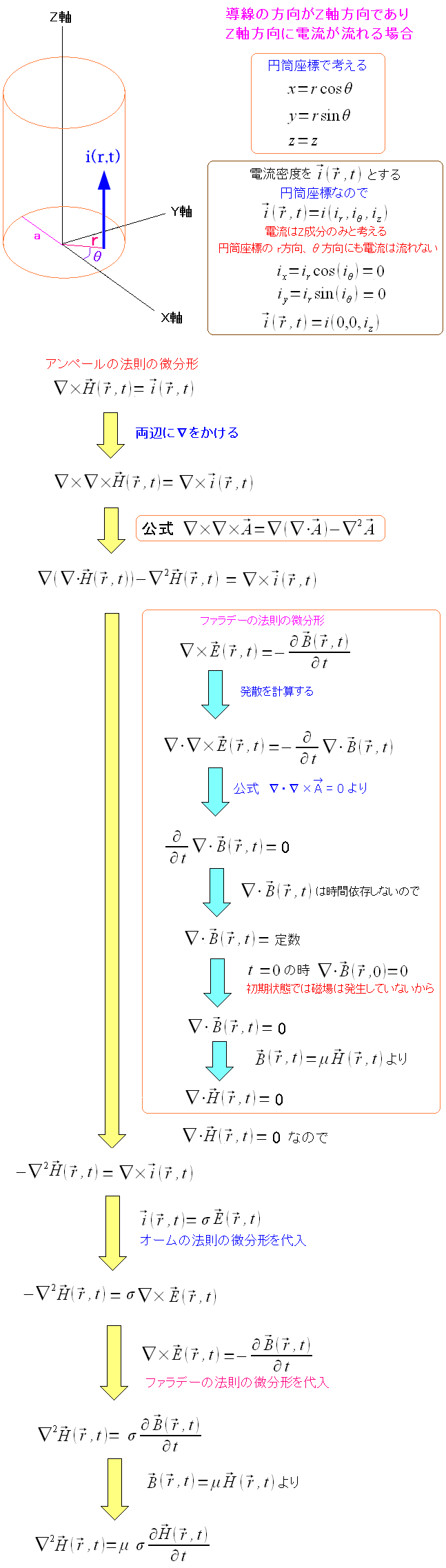 |
| 磁場の微分方程式が求まったのだ。 |
最後に導線内の電流密度の方程式を求める。
| 導線内の電流密度の方程式を求める |
|---|
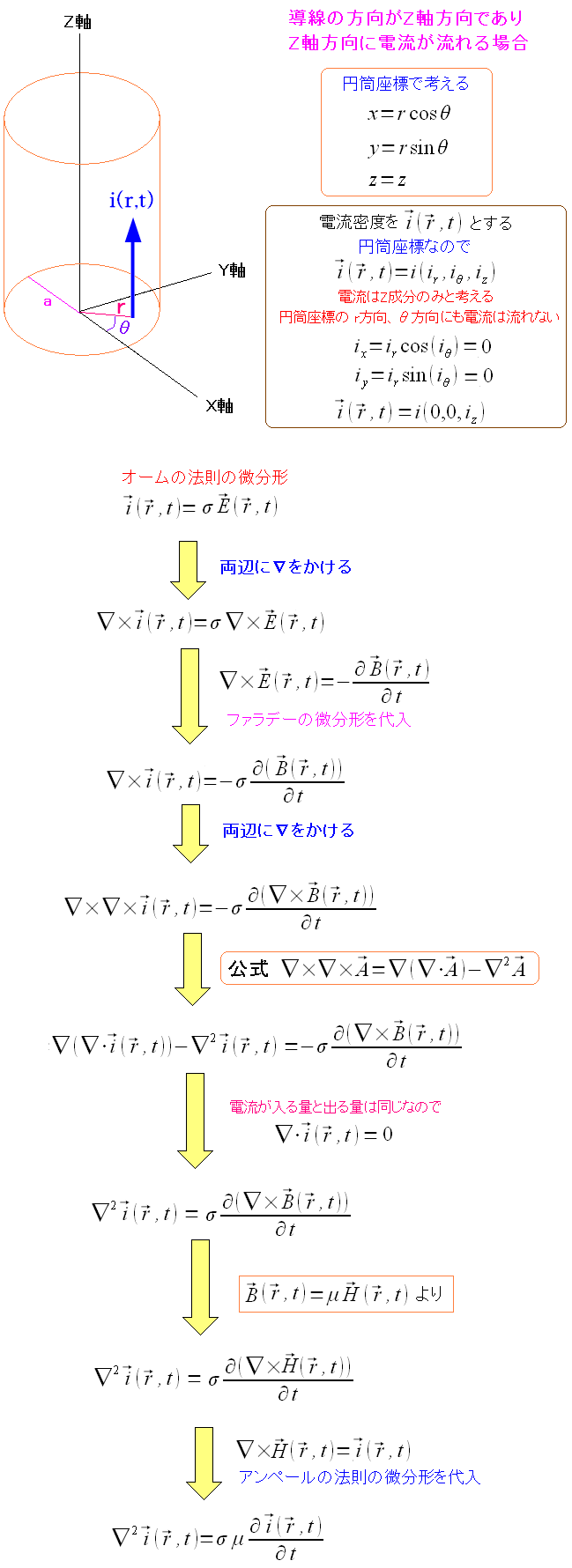 |
| 電流密度の微分方程式が求まった。 |
求まった3つの微分方程式は以下の通りだ。
| 電流密度、電場、磁場の微分方程式 |
|---|
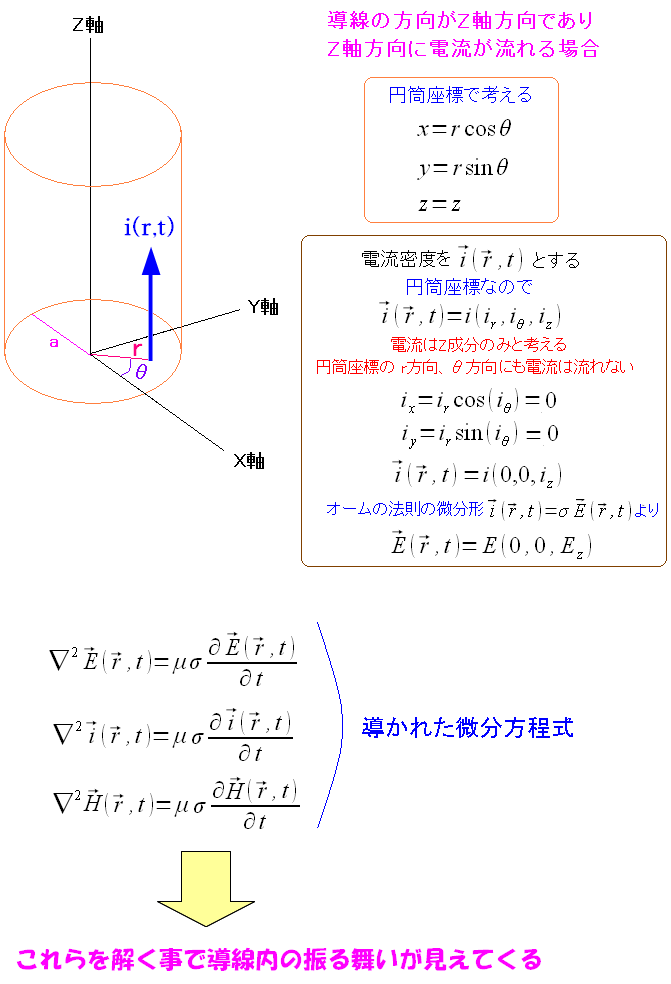 |
| これらの微分方程式を解く事で、導線内の振る舞いが見えるのだ。 |
もちろん数式でなく実験的に導線内の振る舞いを見たいのだが
見るための実験装置があらへん!!
というわけで、数式から導線内の振る舞いを垣間見るしかないのだ。
さて、微分方程式を解く前に、今回、導線をZ軸を中心とする円筒なので
円筒円筒座標系である事を認識する必要がある。
まずは直交座標系と円筒座標系でのrotとラプラシアンの違いを見てみる。
| 直交座標系と円筒座標系でのrotとラプラシアンの違い |
|---|
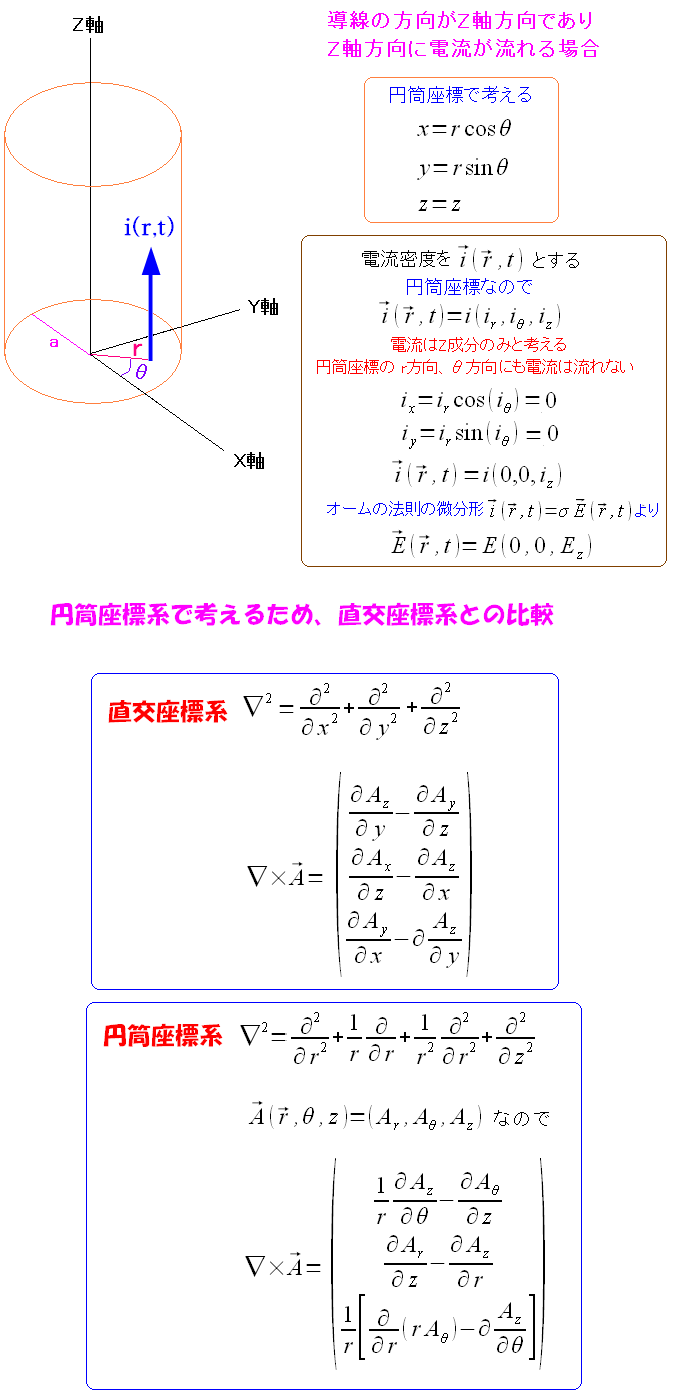 |
| 座標系が変わると、rotもラプラシアンも変わってくるのだ。 |
直交座標系のラプラシアンから、円筒座標系のラプラシアンを求めてみる。
| 直交座標系のラプラシアンから、円筒座標系のラプラシアンを導く |
|---|
 |
|
(どうでも良い愚痴?) 某大学の講義資料を発見し、丸写しだと喜んでいたら、 結構、計算間違いがあり修正していった。 頭の体操にはなったが、めんどくさかった。 ただ、私の計算も正しい保証はないので、偉そうには言えないのだ。 |
さて、表皮効果は、導線の表面に電流が偏り、内部は電流が流れなくなる現象だ。 そこで、電流密度の微分方程式を解いてみるのだ。
| 導線内の電流密度の微分方程式を解いてみる |
|---|
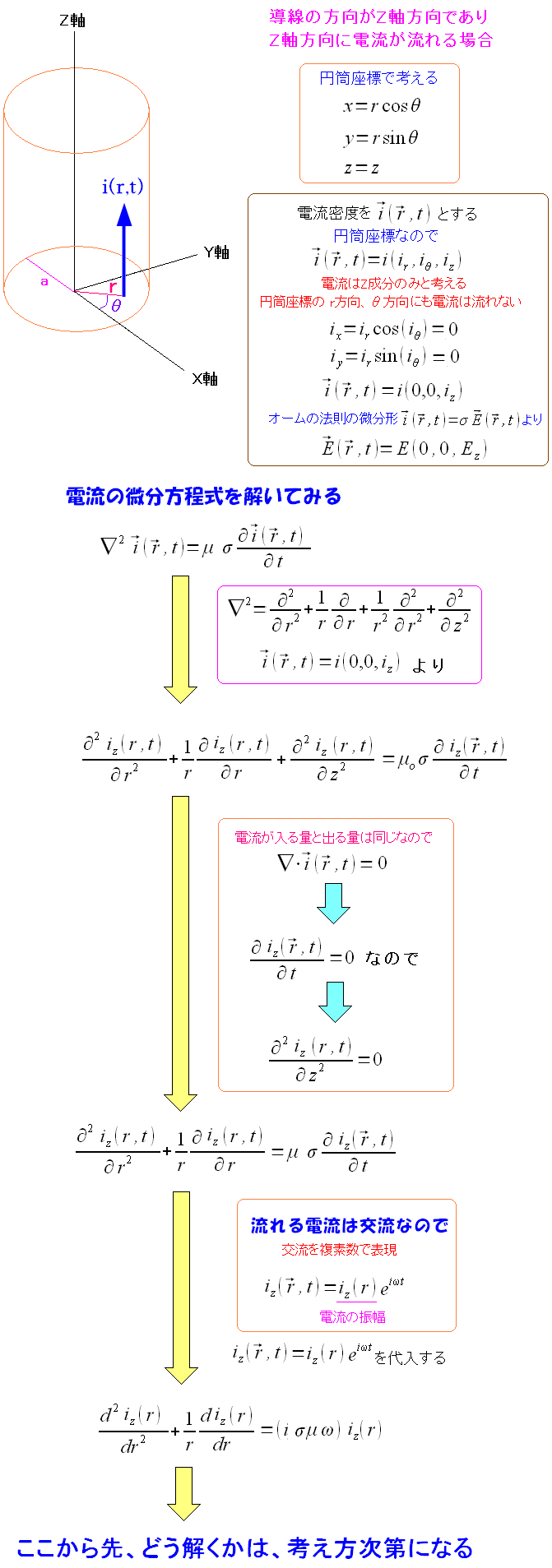 |
| 微分方程式を解こうとするが、厄介な状態になってきた。 |
一体、どないして解くねん!!
なのだ。
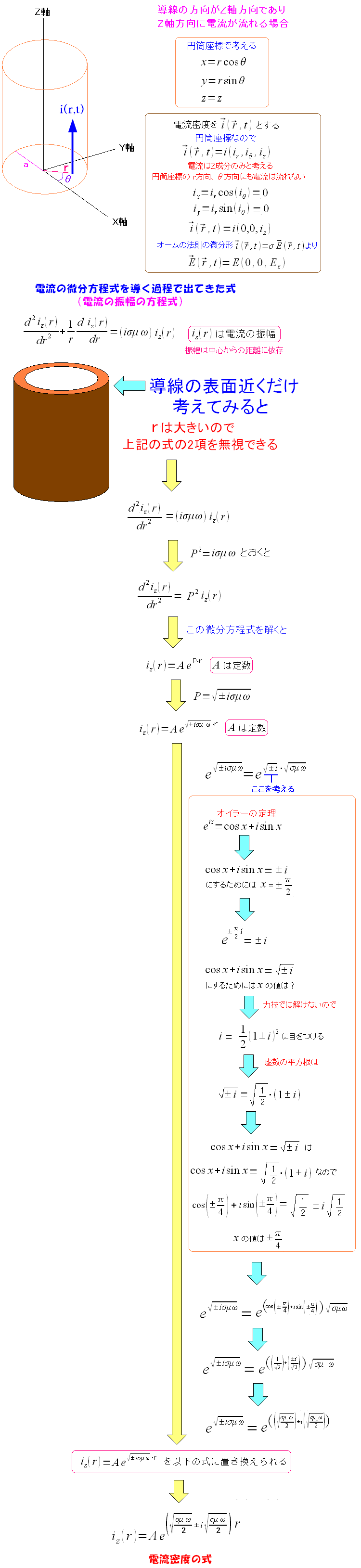
そこで近似式で考えるというのだ。
| 電流密度の微分方程式を近似式で考える |
|---|
 |
|
表皮効果は、導線の表面に電流が偏る現象だ。 そこで導線の半径は大きいと考え、中心部は無視して考える。 そこで上図の方程式の第2項を無視した式を解いていくのだ。 その結果、電流密度の式が解けたのだ。 複素数が混ざっている式になっているが、ここでは気にしない。 三角関数の表現を変えると、複素数が出てくるからだ。 |
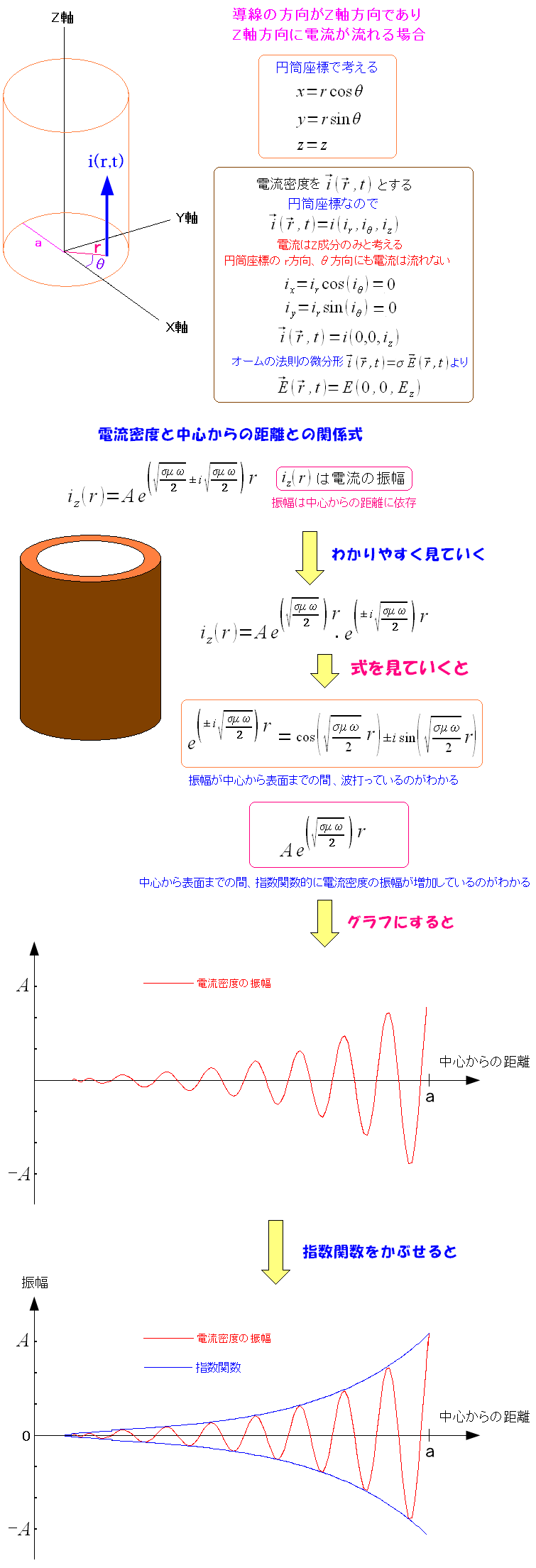
求まった導線内の電流密度(近似式)を見ていく。
| 求まった導線内の電流密度(近似式)を見ていく |
|---|
 |
|
求まった電流密度から、導線の中心からの距離と密度電流の振幅のグラフを描いてみた。 中心になると電流密度が減衰しているのがわかる。 減衰の度合いが指数関数と同じになるのだ。 |
表皮の深さ
表皮効果によって、電流にどれくらいの減衰があるのか、 その目安として表皮の深さ(δ)がある。
| 減衰の目安の表皮の深さ(δ) |
|---|
|
電流の振幅が 1/e倍(0.37倍)になる地点をδで表わし それを表皮の深さと呼んでいる。 導線の表面から、どれくらい深い所まで電流が流れているのかを知るためだ。 |
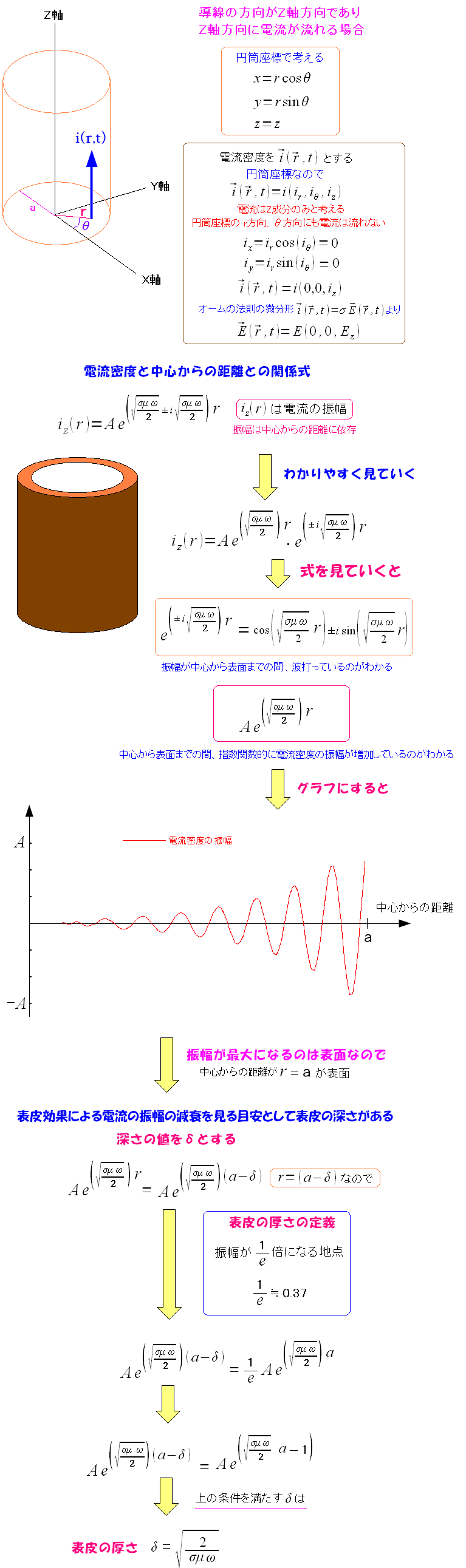
表皮の深さの式を求めてみる。
| 表皮の深さ(δ)の式を求めてみる |
|---|
 |
|
σは物質の電気伝導度だ。 電気の流れやすさの指標の電気伝導度で、オームの法則の微分形で出てきたものだ。 μは物質の透磁率だ。 物質中の磁場の様子の所で出てきたものだ。 ωは交流電流の角周波数。周波数に2πをかけた物だ。 |
交流電流の周波数と物質の違いによる表皮の深さの違いを表にしてみた。
| 交流電流の周波数と物質の違いによる表皮の深さの違い |
|---|
 |
|
物質によって交流電流の振幅の減衰度合いが異なるのがわかる。 ただ、物質に関係なく、中心へ向うほど、電流が減衰しているのだ。 LANケーブルは銅線が使われている。 CAT5e、CAT6、CAT7が、信号を100m送れる事を保証した周波数。 10Base-T/100Base-TXでの信号の周波数と、1000Base-Tの信号の周波数を 銅線上に置いてみた。 なだらかなグラフに見えるが、対数グラフを使っているので 実際には急激に電流の振幅が減衰しているのだ。 |
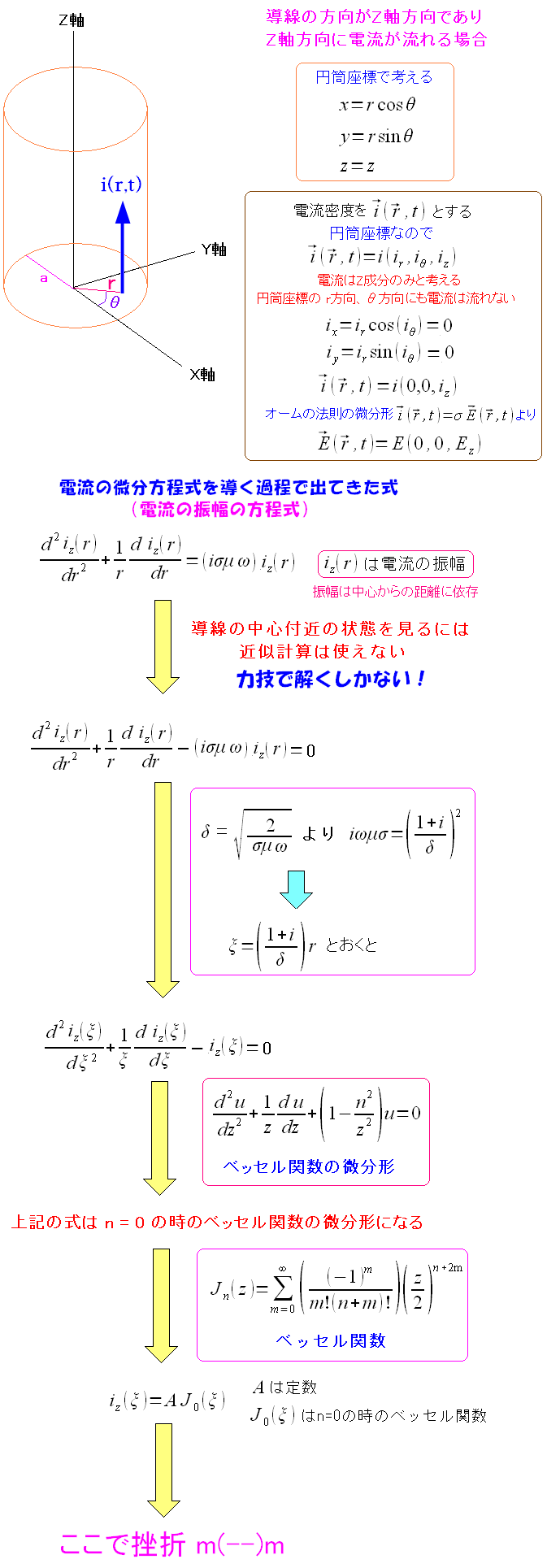
電流密度の微分方程式を近似式にして求めたのだが 頑張って、近似式を使わずに解いてみる努力をしてみたのだ。
| 近似式を使わずに解いてみる努力 |
|---|
 |
|
ベッセル関数が出てきた所で、あえなく撃沈。 私の数学力と、頑張ろうという努力は、この程度に終わったのだ。 |
近似式を使わずに解こうとする努力は、簡単に崩れさったのだ。
表皮効果とポインティングベクトル
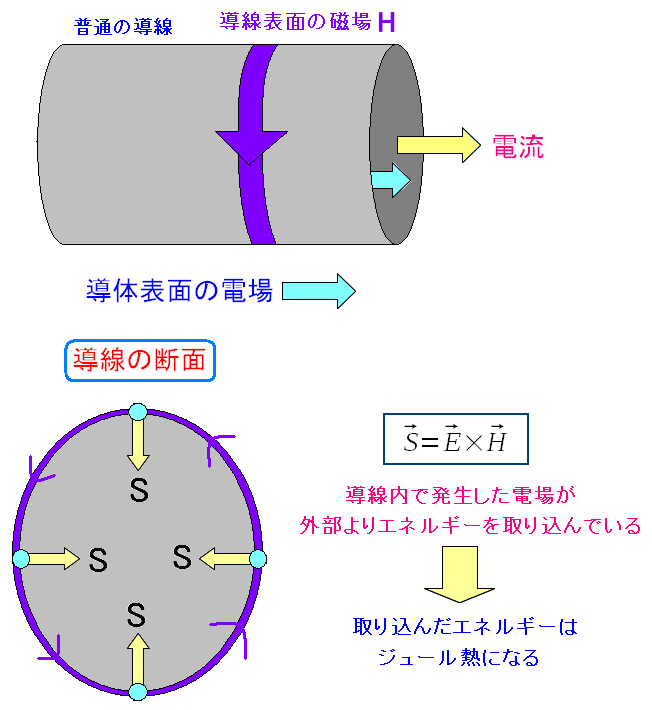
ポインティングベクトルの観点から表皮効果の考察をしてみるのだ。 電気エネルギーは導線の外を伝わるを思い出してみる。 抵抗のある導体は、電線の外を伝わる電気エネルギーを取り込んでいる。
| 導線の外から電気エネルギーを取り込む様子 |
|---|
 |
|
導線表面の電場と電流が作る磁場(アンペールの法則)により 導線の外を伝わっている電気エネルギーを取り込んでいる。 |
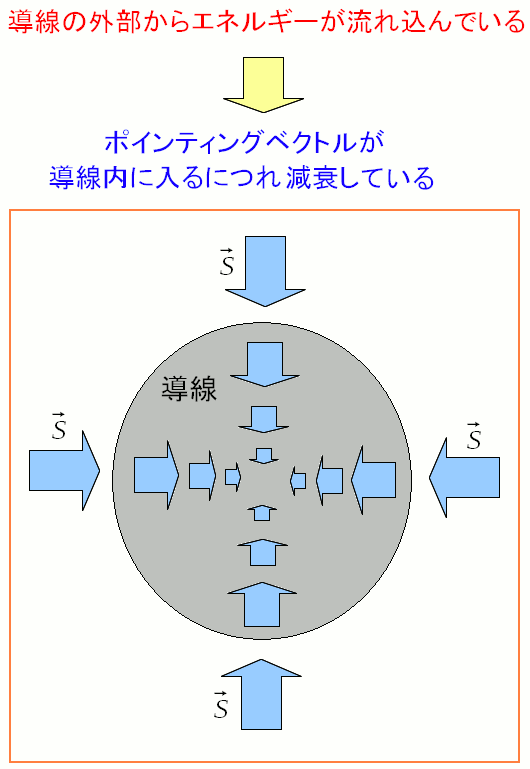
導体内に入ってきた電気エネルギーの流れのポインティングベクトルは導体中で 電気エネルギーが運動エネルギーになっていく事で、減衰していくのだ。
| 導線内部に入るにつれポインティングベクトルは減衰する |
|---|
 |
|
導線の外を伝わっている電気エネルギーを取り込むのだが 導線内に入るにつれ、電気エネルギーがジュール熱に変換されるため 電気エネルギーの流れであるポインティングベクトルが減衰していくのだ。 |
直流だと表皮効果が起こらない
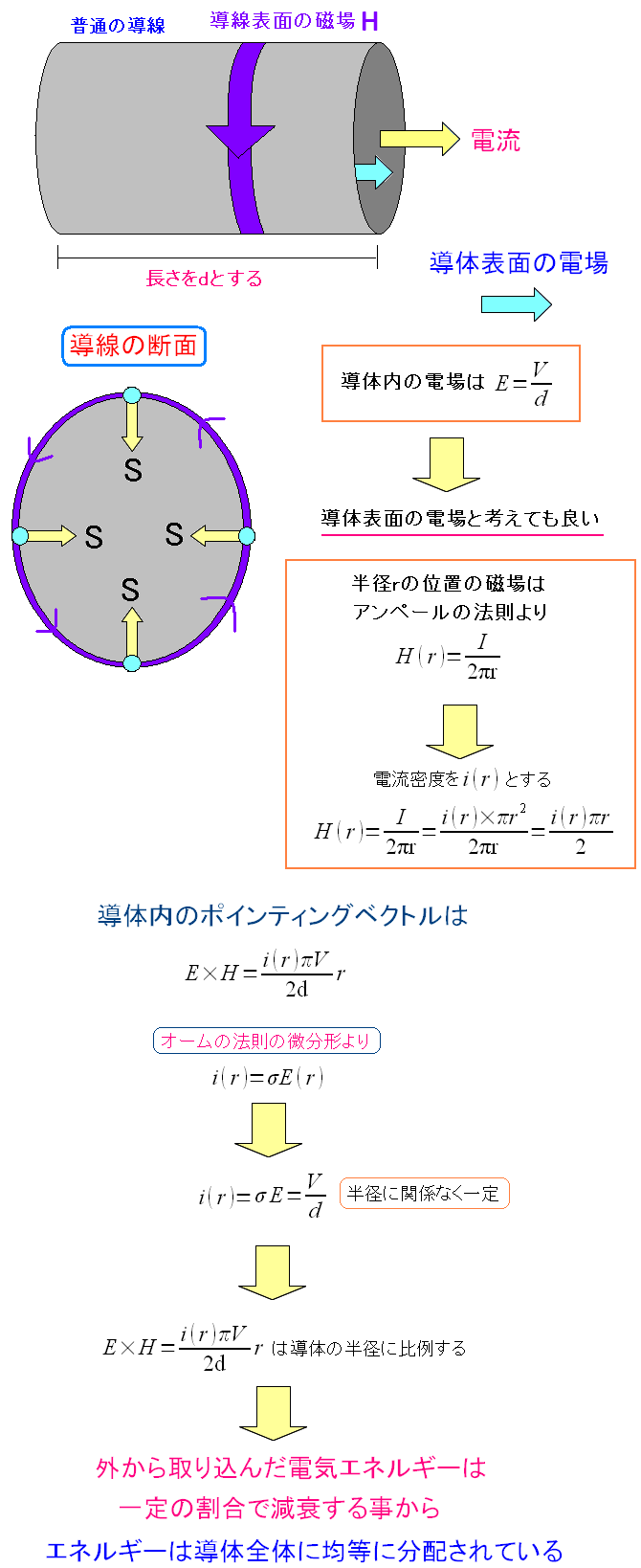
直流の場合を考えてみる。 計算を楽にするため、導線を円筒形と考える。
| 直流の場合、導線の外から電気エネルギーを取り込む様子 |
|---|
 |
|
外から取り込んだ電気エネルギーは、導体内に入っていくと 一定の割合で減衰していく。 オームの法則の微分形より、直流電流の場合 導体内の電流密度は、場所に関係なく、常に同じなのだ。 そのためポインティングベクトルは一定の割合で減衰していくのだ。 |
均等に電気エネルギーが分配されるから、電流密度が一定。 電流密度が一定だから、均等に電気エネルギーが分配される。 なんだか・・・ 循環論法(トートロジー)やん!! 循環論法にならずに、上手に説明するだけの知識は、私にはない。 ただ言える事は、導体内部まで電気エネルギーが入り込むため 均等に分配されている事だけはわかったのだ。交流とポインティングベクトルと表皮効果
交流の場合を考えてみる。 導体内の電場、磁場は既に求めた物があるので、それを使って考える。
| 導体内を流れる交流電流の場合の電場と磁場 |
|---|
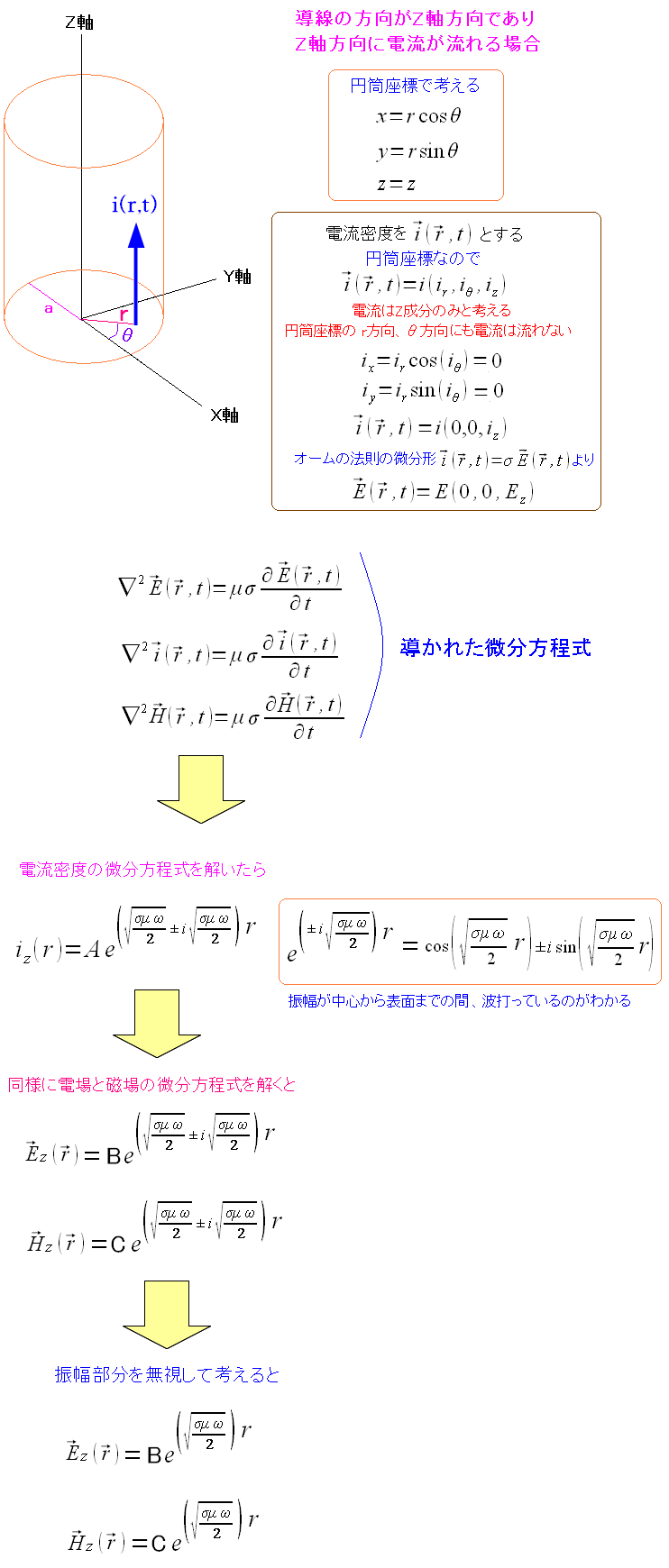 |
| 計算を簡単にするため、電場と磁場の振幅の部分を無視して考えることにした。 |
電気エネルギーが導体内に取り込まれる様子をポインティングベクトルを使ってみてみる。
| 導体に交流を流した場合、導体内のポインティングベクトルの様子 |
|---|
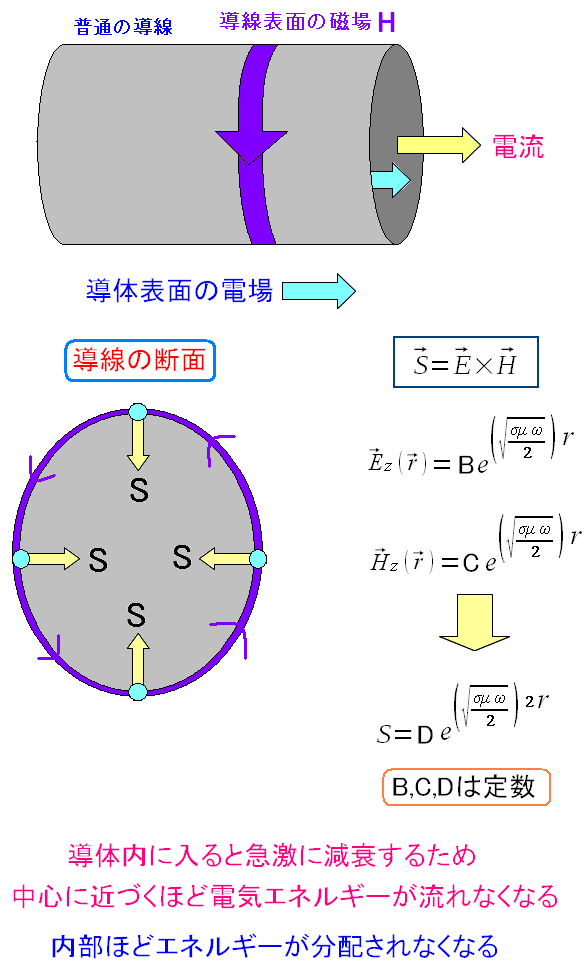 |
|
外から取り込んだ電気エネルギーは、導体内に入っていくと 急激に減衰していくのが、数式からわかる。 周波数が上がる事は、各周波数(ω)の値が上がるため 数式通り、減衰度合いの急激さが増すのだ。 内部に入っていくと運動エネルギーに変換できる電気エネルギーがなくなるため 中心近くでは、ほとんどエネルギーが分配されないため、電流が流れなくなるのだ。 |
ポインティングベクトルで考えると、違った角度で表皮効果が見えてくる。
電磁気学入門の目次
| 電磁気学入門:目次 | |
|---|---|
| スカラーとベクトル | 簡単なスカラーとベクトルの話です。 ベクトルは方向と大きさを持つ量。方向という量持っているだけに注意が必要です。 |
| 静電気の発見からクーロンの法則 | 今でこそ当たり前の静電気や導体、絶縁体、電荷など どういう経緯で発見し、クーロンの法則まで至ったのかの話です。 |
| クーロン力、電場、近接作用 | 4つの力のうち、クーロン力の位置づけ 電荷が作り出す作用の電場。近接作用の話です。 |
| 微分、全微分、方向微分 | 簡単な微分、全微分、方向微分の話です。 ここをしっかり押さえないと、電磁気の数式の意味が わからなくなります。 |
| ベクトル解析 |
電磁気に必要なベクトル解析の話です。 勾配(grad)、2次元のグリーン定理 ストークスの定理の話です。 |
| 電位ポテンシャル | 電位ポテンシャルです。勾配と電場の関係を使って説明しています。 |
| 電気双極子 |
電気双極子の話です。 物質中で起こる分極を理解するのに必要です。 |
| ガウスの法則 | ガウスの法則の積分形、微分形の話です。 |
| ポアソンの方程式、ラプラス方程式 |
ポアソンの方程式、ラプラス方程式の話です。 単に電荷分布から電位を求めるだけの話にとどまらない 奥が深い分野です。ポテンシャル論、デルタ関数 グリーン関数、固有値問題について触れています。 |
| 静電場と渦なしの法則 |
静電場で、電荷を1周させた時の仕事はゼロ 微分形と微分形の渦なしの法則の話です。 |
| ビオサバールの法則 |
電気と磁場の関係の発見の話から ビオ・サバールの法則が導かれるまでの話です。 |
| 磁気双極子 |
磁気双極子の話で、回転電流になります。 物質中の磁場の話にも関連します。 |
| アンペールの法則 |
アンペールの法則の話です。 積分形・微分形だけでなく、閉回路に流れる電流が作る 磁気双極子の話なども書いています。 |
| ローレンツ力 |
磁場中を移動する電荷にかかる力(ローレンツ力)の話です。 ローレンツ力は相対性理論が絡んでいる事も紹介しています。 |
| ファラデーの誘導起電力の法則 | ファラデーの誘導起電力の話です。 |
| うず電流を使った簡単な物理実験 | 電力計に使われるアラゴの円盤。 そしてIH調理器で熱するために発生させる、うず電流は レンツの法則から電流が発生する原理を応用した物だ。 アラゴの円盤の実験と、IH調理器を使った実験です。 気分転換で読んでください。 |
| ベクトルポテンシャル |
わかりにくいベクトルポテンシャルの話です。 電位は電荷が作る電気のポテンシャルだが ベクトルポテンシャルは電流が作る磁場のポテンシャルの話です。 |
| オームの法則の微分形 | 微小領域でのオームの法則の話です。 |
| マックスウェルの方程式 |
4つのマックスウェルの方程式を書いています。 電場と磁場の変化を図にする事で rotの回転の意味も理解できます。 |
| ゲージ変換 |
ゲージ(gauge)は物差しの意味です。 マックスウェルの方程式をE(電場)とB(磁場)の関係式から φ(電位ポテンシャル)とA(ベクトルポテンシャル)の関係式に 書き換える際、ゲージ変換が使われます。 ゲージ変換の役目を書きました。 |
| 電磁波 |
マックスウェルの方程式から電波が伝わる様子を 視覚的に見てみる話です。 |
| 回転のrotはベクトルの微分 |
ベクトル解析や渦なしの法則で出てくるrotは ベクトルの微分という話です。 |
| 電磁気学の単位系 | 電磁気学の単位系の話です。 物理量の単位系の指数を見る次元解析 電磁気学の歴史と単位系の変遷について触れました。 |
| 電気泥棒:電気と法律の話 |
電気は物体なのか、無形物なのか。 明治時代に、電気を無断で使った場合、物か、そうでないかで 窃盗罪になるかどうかが裁判で問われました。 ちょっとした科学と法律の話です。気分転換で読んでください。 |
| 数ベクトルと基底ベクトル | ベクトルの話です。 矢印だけがベクトルでない事。 数ベクトルと基底ベクトルの違いの話です。 多様体、反変・共変ベクトルを理解するのに必要です |
| 多様体 | 空間を一般化した話です。 ▽(ナブラ)の正体に迫まります |
| 外積代数 |
外積、テンソルについて書いています。 極性ベクトル、軸性ベクトル 外積は行列で、ベクトルは見せかけの姿だった話です。 |
| ベクトルの双対関係 |
反変ベクトル、共変ベクトル、双対関係 ベクトル解析、外積代数の話 外積、テンソルについて書いています。 |
| ローレンツ力と相対性理論 |
磁場は電場の相対論的効果だった話です。 ローレンツ力を使って、導線が作る磁場を使って説明です。 |
| 微分形式 |
多様体の話の続きです。 座標に依存しない形での関数やベクトルの微分の話です。 ガウスの法則、アンペールの法則、マックスウェルの方程式が 鮮やかな形で表現できます。 ∇(ナブラ)の正体もわかります。 |
| 物理と対称性 |
マックスウェルの方程式をよく見ると対称性があります。 物理の方程式と対称性を数学的な観点でみると 意外なつながりがあるという話です。 |
| マックスウェルの応力 |
電気力線を弾性体(ゴム)とみなして、力の伝わり方などを 説明した考え方です。 |
| 電場エネルギー | 電場が持つエネルギーの式を導いた話です。 |
| 磁場エネルギー |
磁場が持つエネルギーの式です。 手抜きの説明と、直流RL回路を使った説明を書きました。 |
| ポインティングベクトル |
電磁エネルギーの流れ「ポインティングベクトル」の話です。 電磁波でもエネルギー保存則が成り立つ話から ポインティングベクトルを導いています。 |
| 電気エネルギーは導線の外を伝わる |
導線の外を電気エネルギーが流れる話です。 私が誤解した事、その誤解を解いていく過程を紹介しながら 「目からウロコ」にたどり着いた話です。 |
| 物質中の電場 | 物質中の電場の話です。 分極の話をしながら、物質中の電場の話をします |
| 物質中の磁場 | 磁性の話をしながら、物質中の磁場の話をします |
| 物質中のマックスウェルの方程式 | 物質中でもマックスウェルの方程式が成り立つ話です。 |
| 導体に侵入する電磁波 |
導体に侵入する電磁波が減衰していく話です。 表皮効果と同じ「表皮の厚さ」が出てきます |
| 表皮効果 |
目的の表皮効果の話です。 マックスウェルの方程式を解きながら 交流電流の周波数を上げると、表面にしか電流が流れなくなる話です。 |