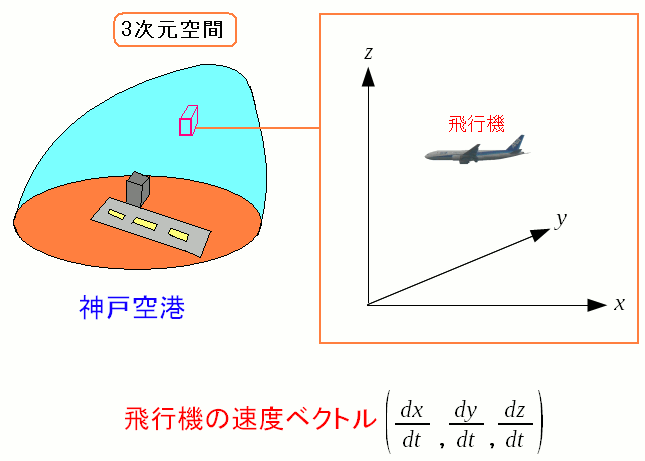
神戸空港に着陸する飛行機に注目してみる。
機長や副操縦士は飛行機の速度を注視している。
大きさだけでなく方向も重要だ。
機長や副操縦士は速度成分を見ているのだ。
システム奮闘記:その105
(2016年5月22日に掲載)
座標系に依存しない表現
▽(ナブラ)の正体を知るため、多様体を勉強する事になった。 多様体の話は長くなるので、最初に多様体を勉強する目的を書きます。
| 多様体を勉強する目的 |
|---|
 |
|
我々、3次元空間に住んでいる。 神戸空港に着陸する飛行機に注目してみる。 機長や副操縦士は飛行機の速度を注視している。 大きさだけでなく方向も重要だ。 機長や副操縦士は速度成分を見ているのだ。 |
3次元の世界に住んでいる我々なのだが、日常では、次の事が前提になっている。
正規直交座標系
なのだ。
| 正規直交座標系が前提になっている |
|---|
 |
|
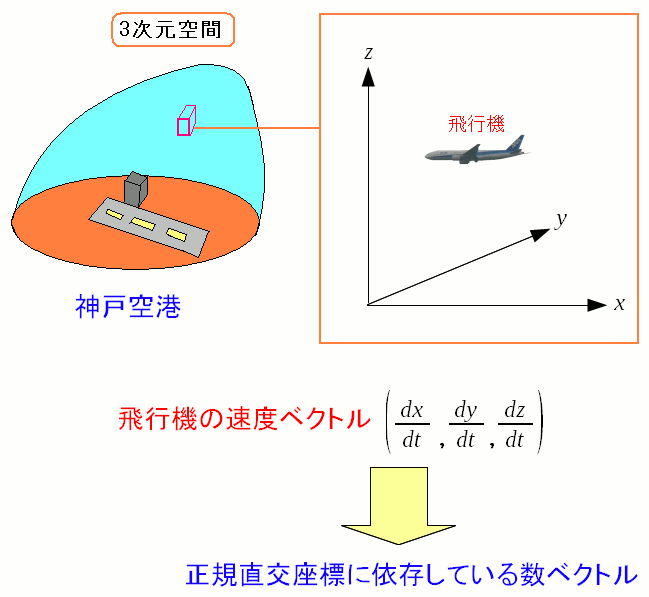
速度ベクトルは、あくまでも正規直交座標系での数ベクトルだ。 普段、基底ベクトルは意識していないのだが、メートルを基準にしていたら 長さ1mの直交ベクトルが、基底ベクトルになる。 ベクトルの話にも出てきたが、もし、座標系が変わり 基底ベクトルが変わると、数ベクトルも変わってしまうのだ。 (注意) 地球は丸いので、実際には飛行機の運航やGPSなどは 正規直交座標が使えるわけではない。 だが、日常、地図などを見ている程度なら、正規直交座標系で十分なのだ。 |
多様体では・・・ 座標系に依存しない表現 の話が重要になる。 そこで座標系に依存する数ベクトルではない 座標系に依存しない速度ベクトル を求めるのだ。
| 座標系に依存しない速度ベクトルの表現を知るのが目的 |
|---|
 |
|
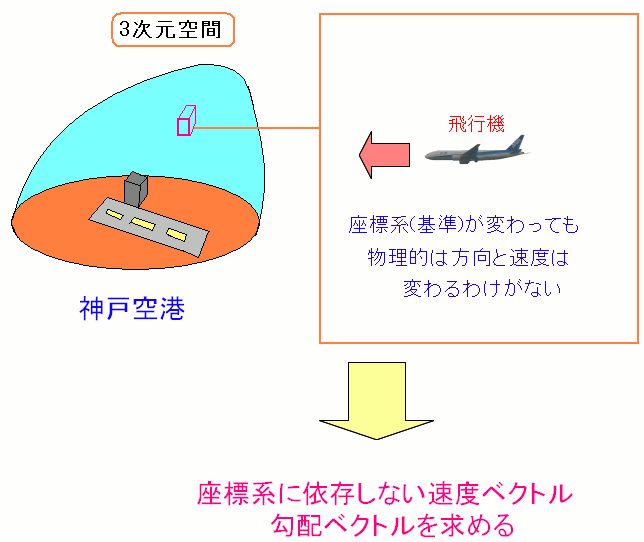
座標系(基準)が変わっても、速度の方向や大きさ、そのものは不変だ。 そこで座標系に依存しない不変の大きさと方向を求めるのが目的だ。 |
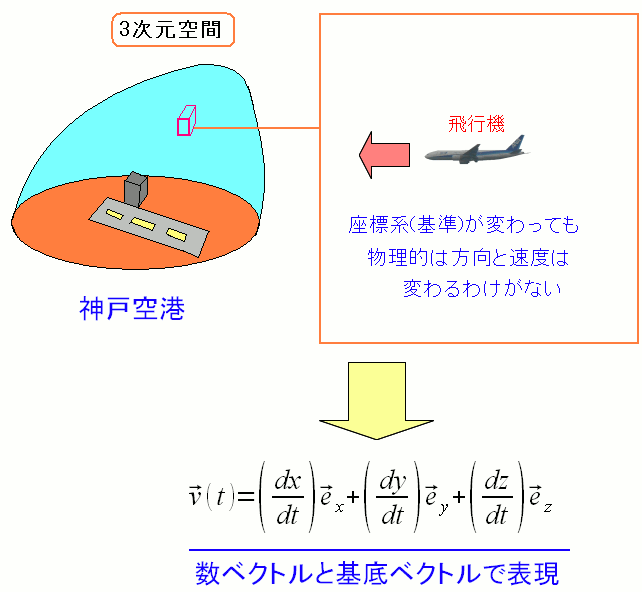
座標依存しない形で速度ベクトルの表現を行なう。 難しそうな話だが、そうでもないのだ。 数ベクトル 基底ベクトルでも書いたが、数ベクトルの表現は、座標依存した形で 基底ベクトルが隠れた表現になっている。 基底ベクトルがあるので、数ベクトルで長さを調整している形になっている。 本当の長さと方向を知るには、数ベクトルと基底ベクトルを使って ベクトル表現すれば良いのだ。
| 数ベクトルと基底ベクトルを使ってベクトル表現 |
|---|
 |
|
数ベクトルのままだと基底が見えないだけでなく、座標依存した形になっている。 そこで数ベクトルと基底ベクトルで本当の長さと方向を見てみる事にする |
隠れていた基底ベクトルを 浮き彫りにする事で 座標系に依存しない長さと方向を見出す というのだ。 神戸空港が出てきたので、どうでも良い余談。
| どうでも良い余談 |
|---|
 |
|
関空へ着陸する間際に撮影した神戸空港と神戸の夜景。 写真では確認できないが、スパコンの京のある理研も含まれているのだ 関空に着陸する飛行機は、和歌山沖の航路と、神戸空港の沖を旋回があるが 飛行機が神戸沖の航路を飛んだ時は、綺麗な神戸の夜景が楽しめるのだ。 (お断り) 航空法改正による電子機器の利用緩和が行なわれた以降に、ANAで撮影した物です。 なので着陸態勢に入っても、デジカメで撮影しても問題ないのだ。 機内での使用が制限される電子機器(ANA) |
多様体の勉強。 自宅の本棚を見ると、20年前に買った本が見つかった。 「多様体の基礎」(松本幸夫:東京大学出版) 学生時代、中学の時の友人に「多様体は面白いよ」と勧められて買った本だ。 だが、当時、読んでみたが、目が点になって、20年間、放置していたのだ。 Y君は東大工学部いた上、博士号まで取得した人物だ。 異様に数学・物理ができたのだ。 Y君の頭のデキが違いすぎたのを考慮しなかったため、買ったまんま、 積ん読になっていたのだ。 でも、20年経って、ようやく当時のY君に追い付きかけた私。 読み進めていくうちに、少しづつ理解したと思いきや・・・ とんちんかんな理解をしていた!! だった。 そのため途中まで作成していた絵をボツにした。
| ボツになった絵について |
|---|
|
独学の場合、勉強する際、誤った理解をする事がある。 誤った事に気づかず、絵を書いていった後で、おかしさに気づいた。 しかも、本の丸写しの内容だったので、全部、ボツにした。 可能な限り、自分の言葉や表現で描かないと わかりにく受け売りの絵になってしまうのだ。 |
わかりやすい資料がないのか探す事にした。 だが、私が学生時代とは違い、ネットの時代。 色々な大学で、講義資料が公開されていたりする。 東工大数学科の川平友規さんの講義資料を発見した。 Past/Current Courses + + Tomoki KAWAHIRA + + 「多様体の基礎のキソ」を読んでいく。 わかりやすい!!!空間
多様体とは空間に関する分野なのだが、いざ空間と言われると 空間って何やねん? となってしまう。
| 空間とは |
|---|
 |
|
空間というと、写真のような、我々がいる3次元空間を連想する。 (写真について) ちなみに写真は「天空の城・竹田城」で撮影したものだ。 兵庫県民なので、兵庫県朝来市にある竹田城を宣伝しておくのだ |
だが、数学では空間は3次元とは限らない。 そして「空間」の定義があるのだ。
| 空間とは構造を持った要素の集合体 |
|---|
 |
|
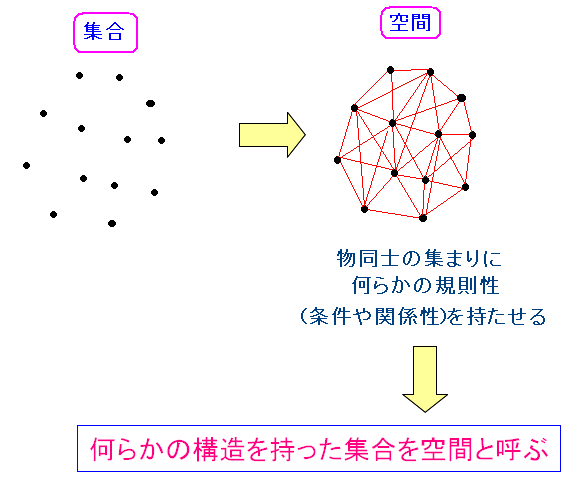
空間は空っぽではなく、色々な要素の集合体なのだ。 単なる集合体だと空間とは呼ばない。 要素同士の間に、何らかの構造(四則演算や距離など)を持たせて 空間というのだ。 |
要素同士の間で、何らかの構造を持った集合体。
| 1次元でも2次元でも空間 |
|---|
 |
|
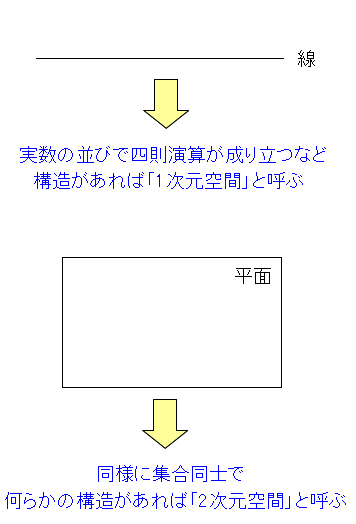
1次元でも2次元でも、要素同士に何らかの構造があれば 空間と言える。そのため1次元空間、2次元空間と言う。 日常生活では、空間といえば3次元を連想するため 少し違和感を覚えても不思議ではない。 |
ここから道のりが長いので概略を先に説明する事にした。
| これから書く多様体の話の概略(1) |
|---|
 |
|
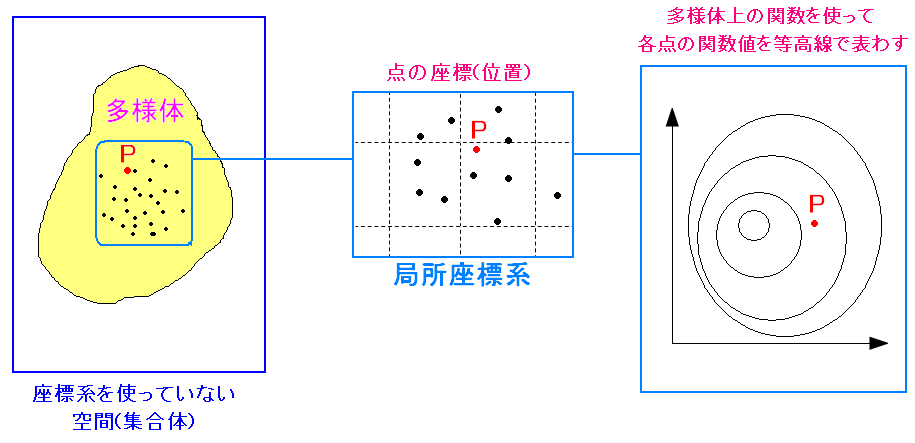
多様体は座標系を定義していない空間だ。 だが、一部の領域では局所座標系が適用できるのだ。 適用できる範囲の領域の点を、多様体上の関数を使って 等高線を描くのだ。 平たく言うと、近くの空き地へ行って、定規を使って空き地の座標を決めて その位置での温度や気圧の分布を調べて、等高線として描くのと同じなのだ。 |
描いた等高線には意味がある。
| これから書く多様体の話の概略(2) |
|---|
 |
|
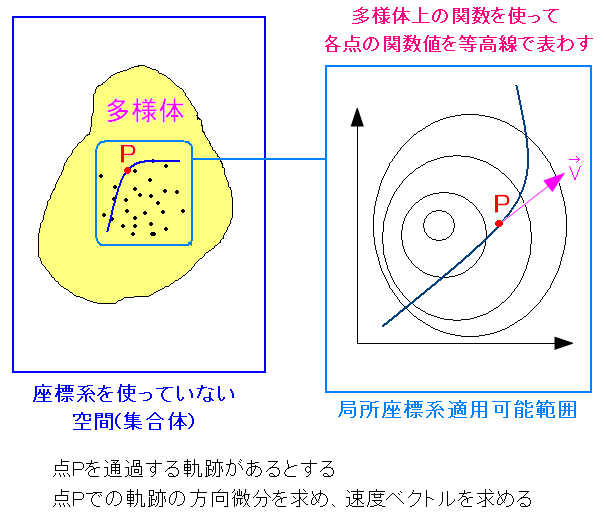
点Pを走り抜ける軌跡を考える。 軌跡こそ、まさに方向微分の方向なのだ。 点Pでの方向微分を求め、その際に出てくる速度ベクトルを求めるのだ。 多様体上の速度ベクトルなので、座標系に依存しない物なのだ。 |
座標系に依存しない多様体上の速度ベクトルを求めるのが目的なのだ そんなもん、なんでいるねん となる。 だが、速度ベクトルを求めるといっても、座標系に依存しない形を求めたり そこから発展して、局所座標系の基底ベクトルを求めたりするなどがある。 ∇(ナブラ)の正体を知るための準備 なので、この段階で、何をしようとしているのか、わからなくても とりあえず、ここは我慢して読んで欲しいのだ。 多様体とは何かをみていく事にした。局所座標系
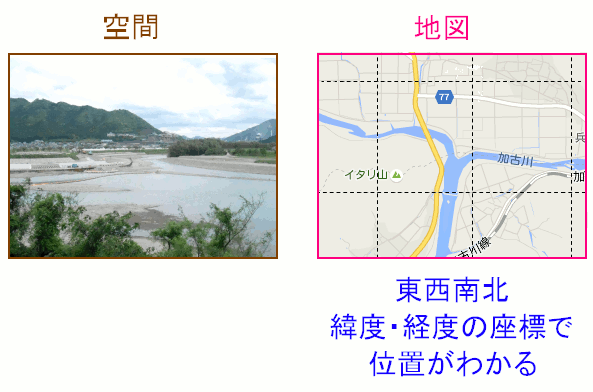
| 空間と地図(座標系) |
|---|
 |
|
空間そのものだと位置がわからない。 我々の世界でも、目の前の光景を見ても、地図がないと、どこにいるのか、わからない。 そのため、どこにいるのかを知るために地図が必要になる。 (写真について) 播磨国(兵庫県西脇市黒田庄町)から丹波国(兵庫県丹波市山南町)を見た景色だ。 山南町にある円応教の建物や兵庫パルプ、加古川が分かれている姿が見える。 ちなみに西脇市黒田庄町は、黒田官兵衛の生誕の地だ。 2014年の大河ドラマでは姫路出生説を採用しているが、黒田庄説の方が有力なのだ。 |
播磨国も丹波国も地球表面にある。 その時、地球の、どの位置にあるのか知る必要がある。
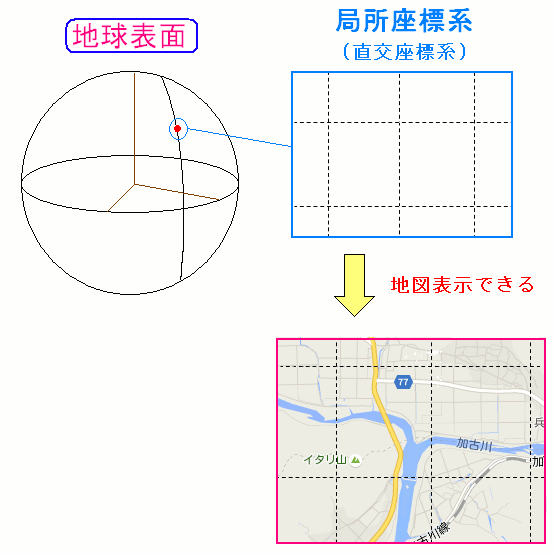
| 地球表面と局所座標系 |
|---|
 |
|
地球の表面は2次元だ。なので2次元の座標系が使われる 地球は円形なので表面も厳密には平らではない。 局所部分だけ取り上げると、平らとみなせるので直交座標系が適用できる。 |
ところで局所座標系がでてきた。 どんな座標系なのか。
| 局所座標系について |
|---|
|
空間の微小領域に適用する座標系を局所座標系という。 微小領域なので、まるでミクロの世界を連想してしまいそうなのだが あくまでも相対的な大きさの違いなので、地球の表面で考えると 1Km四方の地図も微小領域になるし、局所座標系として 直交座標系が採用できるのだ。 |
より広い範囲を見たい場合は、局所座標を重ね合わせる事ができる。
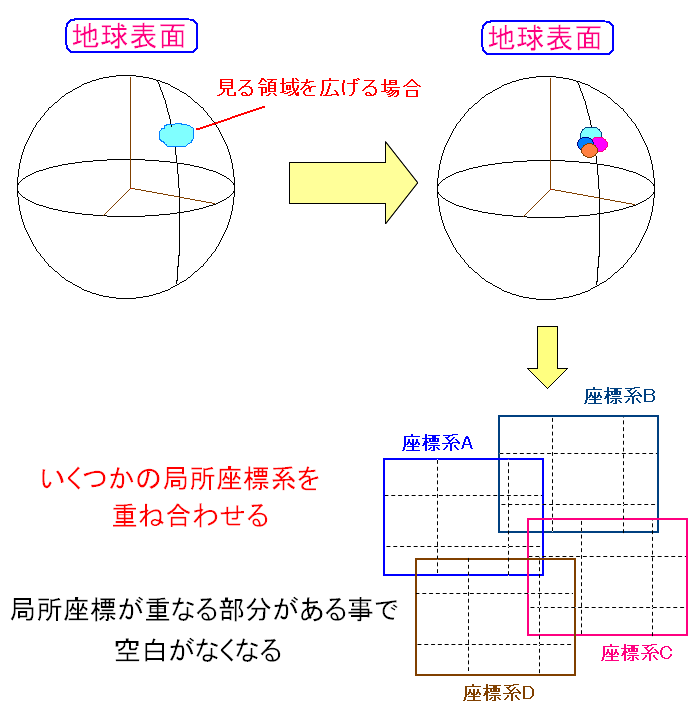
| 局所座標を重ね合わせる |
|---|
 |
|
局所座標が重なり合う部分ができるが、それは問題ない。 むしろ空白部分がなくなるので良いのだ。 (座標系が重なっている場所) 局所座標系が全て直交座標系になるとは限らない。 そのため重なりあっている部分は、座標変換が必要なのだが ここでは取り上げないのだ。 |
いくつもの局所座標系を重ねた結果、より広い範囲を見る事ができる。
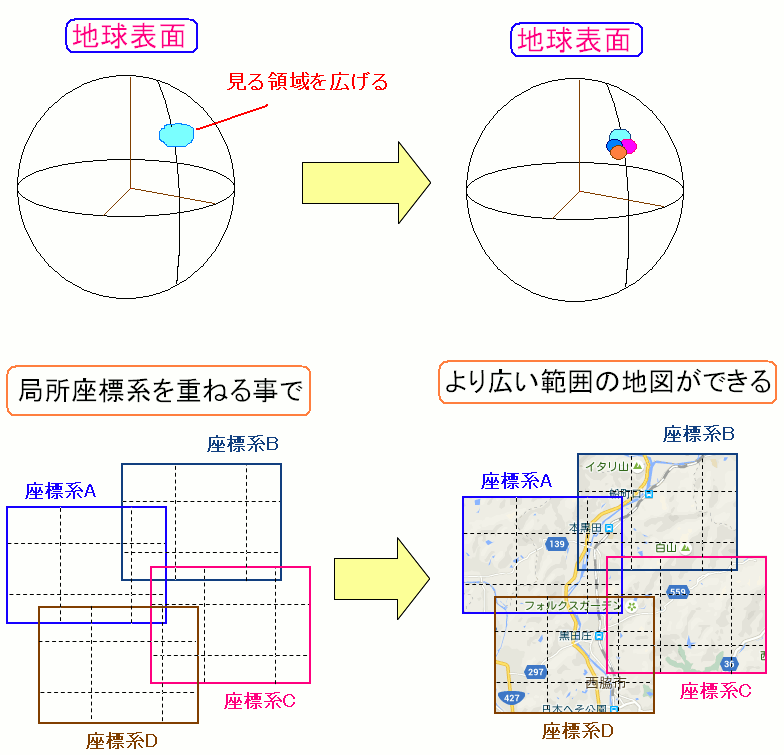
| 局所座標系を重ねた結果、より広い範囲を見る事ができる |
|---|
 |
|
いくつもの局所座標を重ね合わせる事で、より広範囲にある物体や施設の 位置(座標)を知る事ができる。 南方向に広げると、黒田官兵衛の生誕の地「荘厳寺」や 日本の中心の西脇市の「日本のへそ公園」の位置までわかる。 |
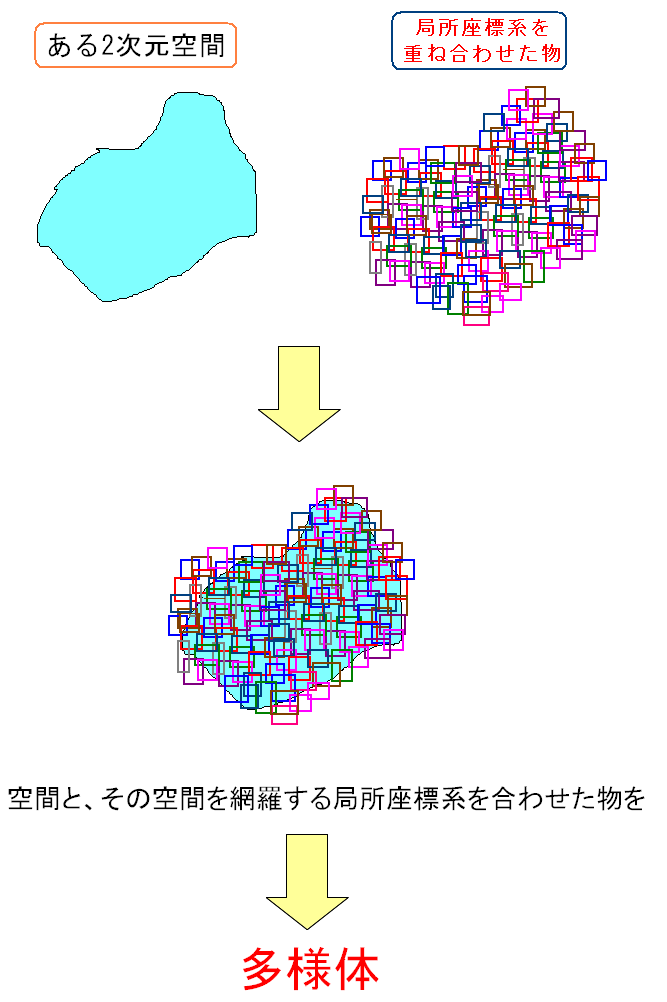
平面空間だけでは位置がわからない。 そのためには座標系が必要な事を書いた。 さて、多様体とは大雑把に書くと、以下の事なのだ。
| 多様体とは(大雑把な説明) |
|---|
 |
|
空間と、それを覆う座標系を合わせて「多様体」という。 単に空間だけの事を多様体という場合もあるようだ。 (注意) あくまでも大雑把な説明なのだ。 厳密な定義をしないと数学の先生には怒られそうなのだが 多様体を知るのが目的だし、私も厳密な定義が理解できないのだ 大雑把な説明だけする事にした。 |
だが、上の内容だと不十分だ。
多様体の定義に使われる空間とは
位相空間
というのだ。
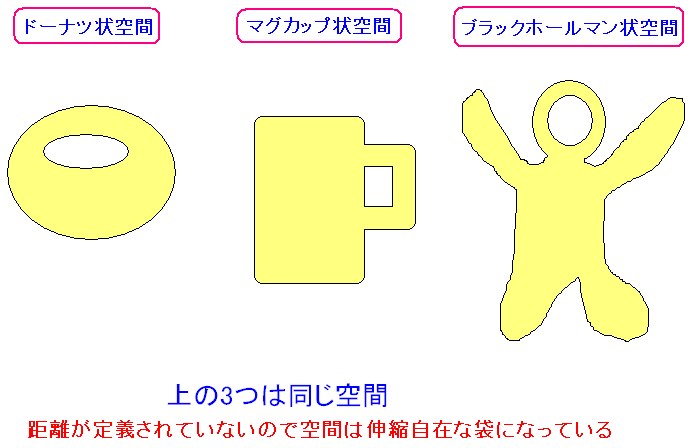
| 2次元の位相空間(3つの空間は、どれも同じ) |
|---|
 |
|
数学科で習う厳密な定義は、ここでは書かないし、書けない。 位相空間とは点で満たされた空間だ。 2次元の位相空間を描いた物だ。 だが、距離が定義されていないため、伸縮自在になる。 ドーナツも、マグカップも同じとみなす。 (余談) 一番右にあるのはキン肉マンで出てきたブラックホールマン。 でも、若い人は知らないだろうなぁ・・・。 |
感覚的には位相空間は・・・ 得体が知れぬ空間 かもしれない。局所座標系の適用
距離が定義されていない空間。しかも伸縮自在。 そんな空間を直接見る事はできない。 我々は空間の状態を座標系を通じてしか見るしかないのだ。
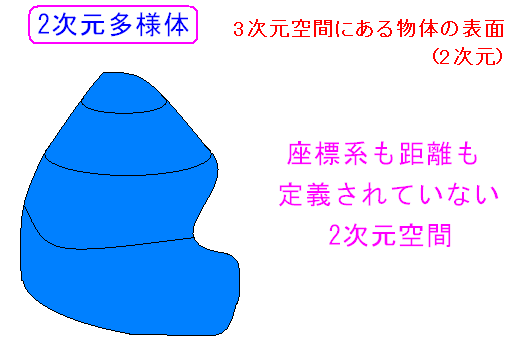
| 位相空間のままだと |
|---|
 |
|
2次元位相空間のままだと、空間がどうなっているのか 空間の性質などを考える事はできない。 |
集合体の個々の要素の位置を知るためには、人間が作った座標系を使う必要がある。
多様体上は、デコボコしていたりする事もあるので、微小領域で使える
局所座標系を適用する
というのだ。
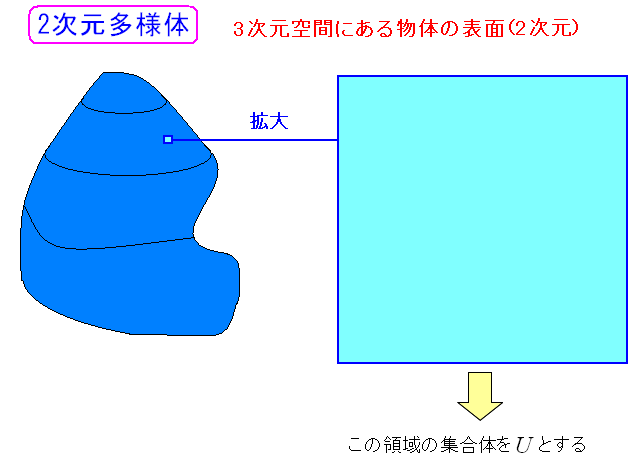
まずは、多様体の領域の適当な場所を拡大してみてみる
| 多様体の領域の適当な場所を拡大してみてみる |
|---|
 |
|
この時点では、座標系も何も定義していない 単に集合が詰まった空間なのだ。集合体の事を「U」としておく。 |
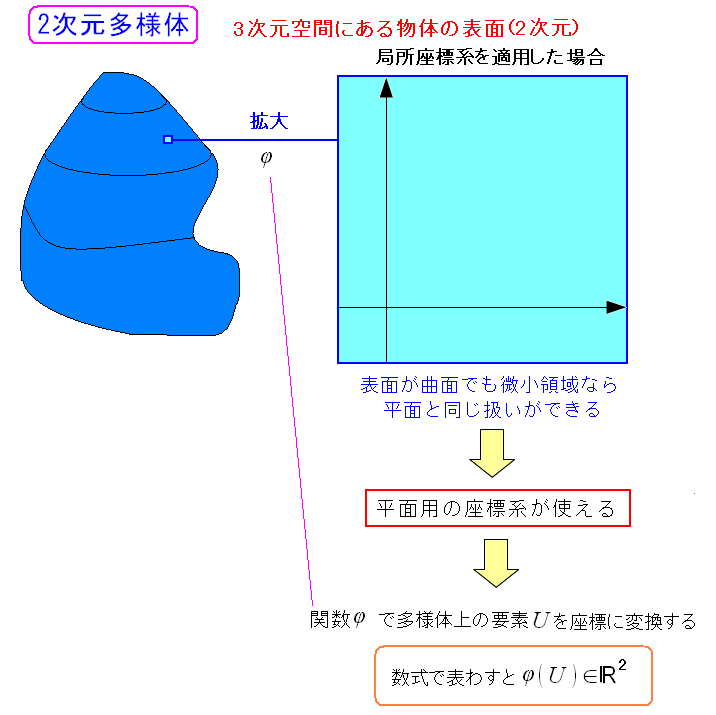
そこで集合体(U)の、それぞれの要素の位置を把握したいため 適用できる局所座標系を適用してみる。
| 局所座標系を適用してみる |
|---|
 |
|
要素を局所座標系の座標(位置)に変換する座標変換関数をφとする。 φによって、要素と座標を関連づける事ができる。 ここでは直交座標系を適用してみた。 |
速度ベクトル
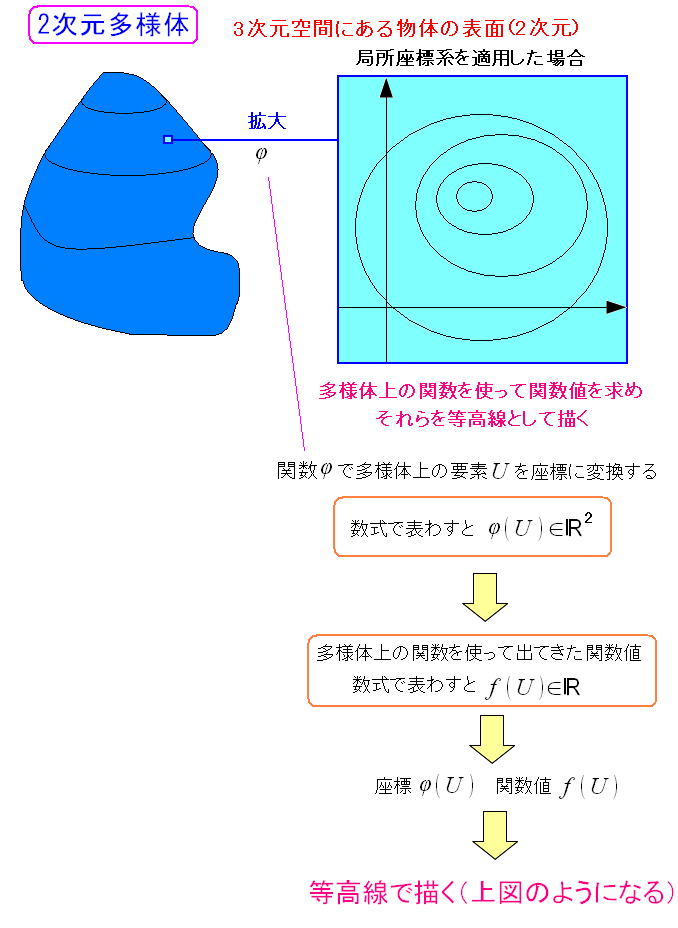
次に多様体上の関数を使って、各要素の座標と、各要素の関数値を結びつけて 等高線を描いてみる。 言葉では難しくなっているが、平たく言えば、地面の温度分布を知りたい時 地面の座標を決めた上で、地面の温度状態を分布図(等高線)に描く事なのだ。 座標と温度を関連づける関数が、多様体上の関数に当てはまる。 そう考えると・・・ 日常でもやっている行為 なのだ。
| 多様体の要素の関数値を使って等高線を描く |
|---|
 |
|
要素から座標は、座標変換関数φで関連づける事ができる。 ここでは直交座標系を適用してみた。 要素から関数値は、多様体上の関数で決める事ができる。 座標と関数値との関連付けを図にすれば、等高線を描く事ができる。 |
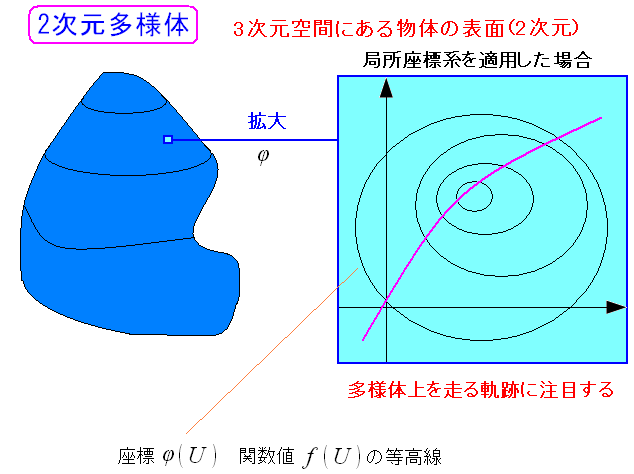
次に多様体の領域を走る軌跡があるとする。 その軌跡に注目してみる。もちろん座標変換関数φによって座標と関連づける事ができる。
| 多様体の領域を走る軌跡に注目する |
|---|
 |
|
方向微分の所で、火渡りの例を出したが、ここでも等高線上を横切る 軌跡があるとする。パラメーターを「t」にしている。 時間(t)と思っていただいて問題はない。 |
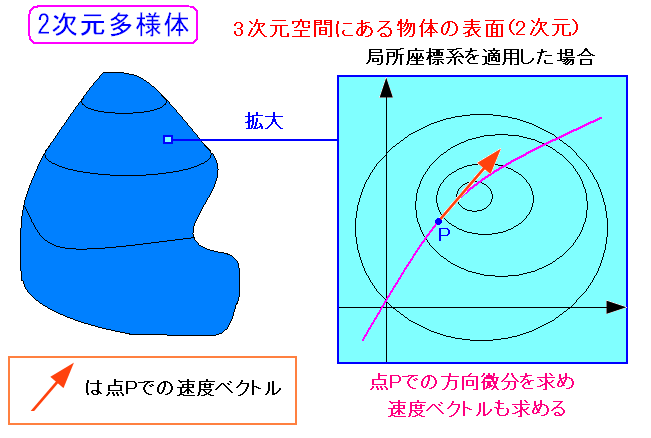
軌跡のある点(点P)での速度ベクトルを見てみる
| 軌跡のある点(点P)での速度ベクトルを見てみる |
|---|
 |
|
点Pでの速度ベクトルを見てみる。 点Pでの速度で矢印の方向なのだ。 |
回り道をしているようだが
正面突破できへんから回り道
なのだ。
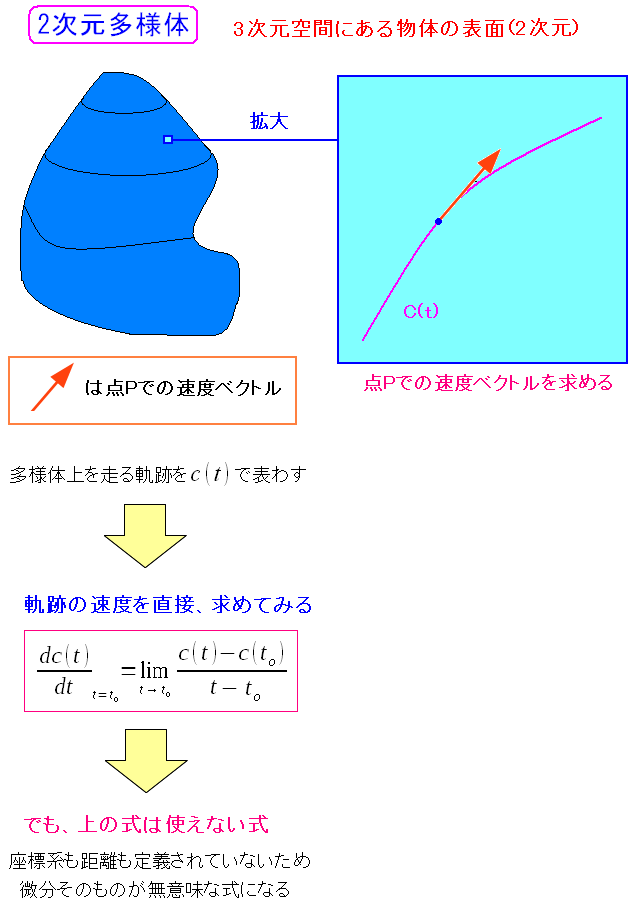
| 座標系が決まっていない空間での軌跡を時間(t)で微分しても無意味 |
|---|
 |
|
多様体そのものは、座標系を定義していない。 そのため「t」で微分した所で、変化量も向きも何もわからない。 |
多様体で見ている範囲に、座標系を適用できたとする。
でも、この時点でも
正面突破できへんから回り道
なのだ。
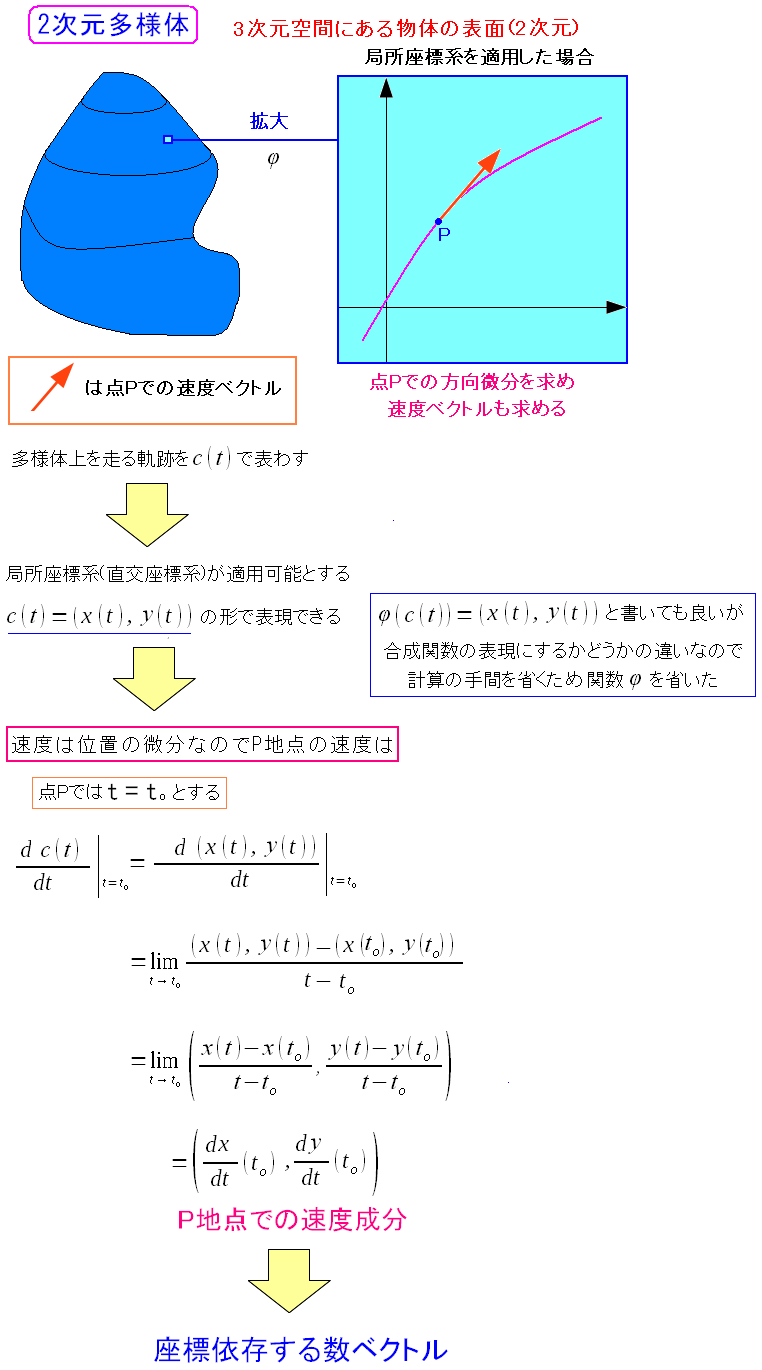
| 座標依存する速度ベクトルになってしまう |
|---|
 |
|
軌跡を座標変換する関数φによって、座標と関連づける事ができる。 座標を関連づけた所で、時間(t)で微分すると、速度ベクトルが出てくるが 求まった速度ベクトルは、数ベクトルなので、座標依存した物になっている。 |
基底ベクトルを求めてみる
数ベクトルだと座標依存してしまう。 そこで多様体上の関数を使って、等高線を描いた上で 方向微分を使って、基底ベクトルを求める。 それによって、座標に依存しない形での速度ベクトルを求めるという 回り道をするのだ。
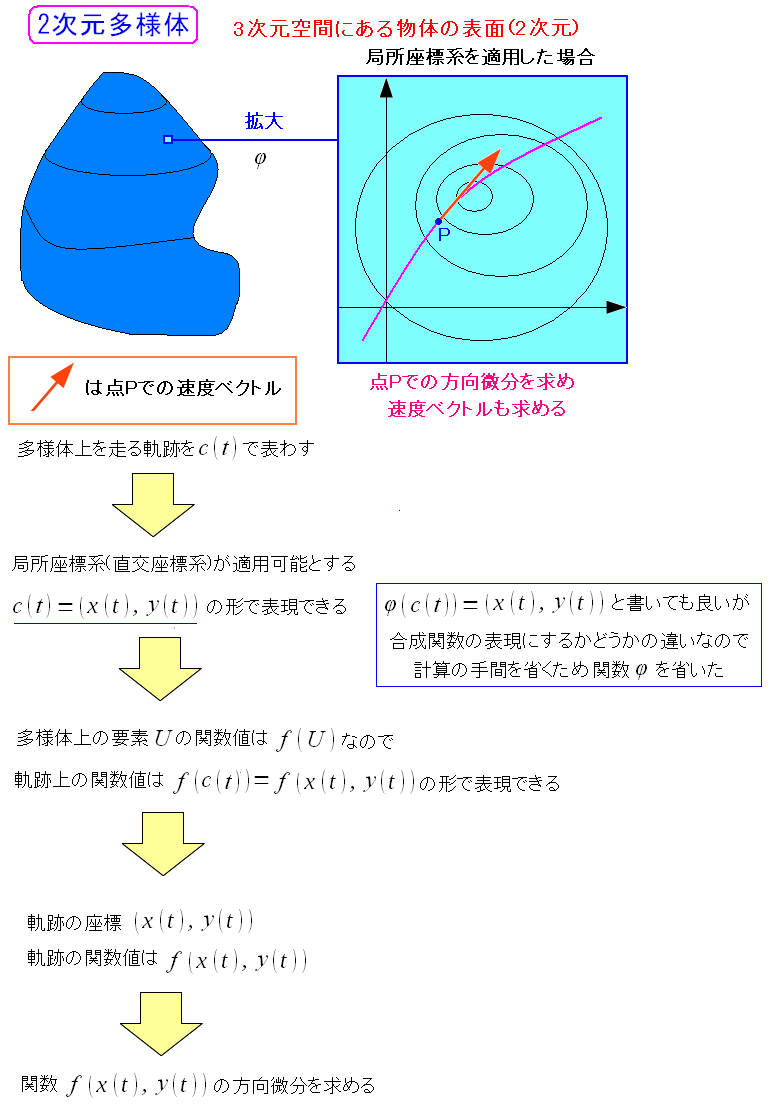
| 軌跡と多様体上の関数を関連づける |
|---|
 |
|
多様体上の関数と書くと仰々しくなるのだが 多様体上の要素と温度を関連付ける関数だったり 要素と気圧を関連づける関数だったりする。何でも良い。 軌跡を多様体上の関数と関連付ける事で、方向微分を求める事ができる。 上図だと点Pでの方向微分(点Pでの軌跡の方向)を決める事ができる。 |
方向微分を求めてみる。
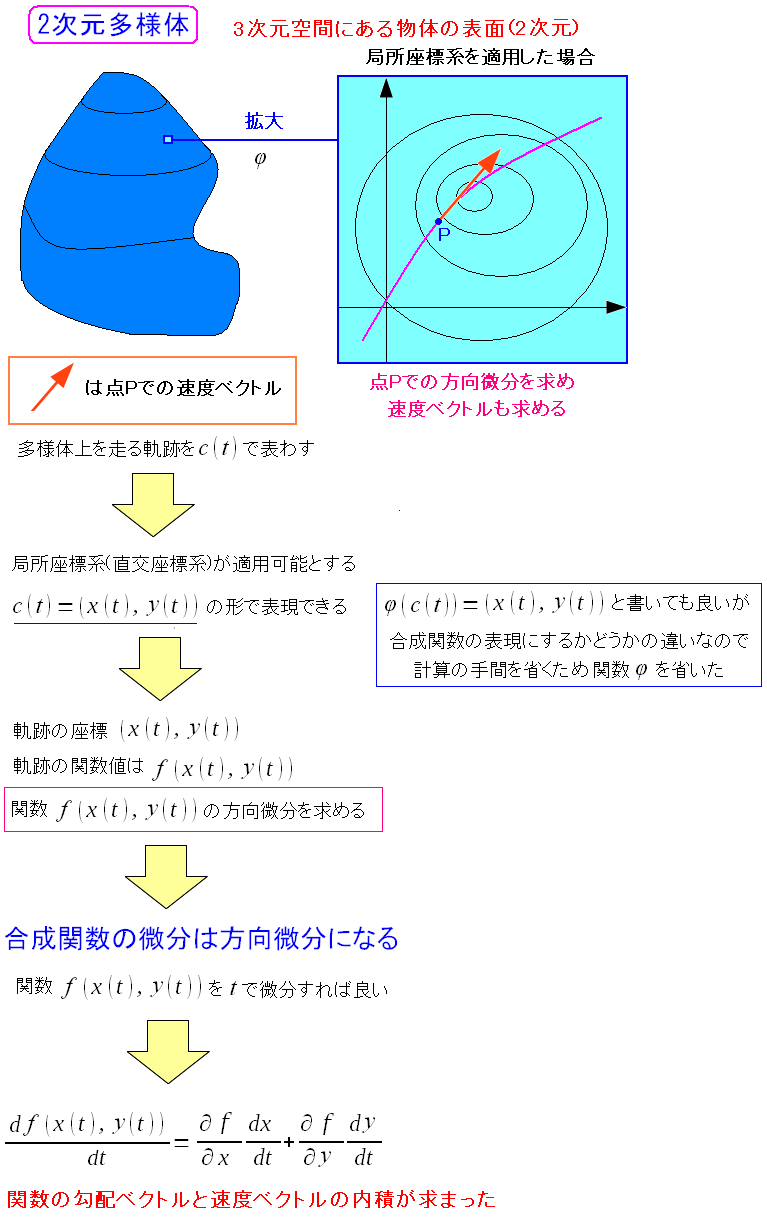
| 方向微分を求めてみる |
|---|
 |
|
方向微分だが、難しく考える必要はない。 最初の微分の話で、合成関数の微分は方向微分と説明したのだ。 軌跡の座標(x(t),y(t))も、関数tの関数なので、f(x(t),y(t))は合成関数だ。 そのため時間(t)で微分すると、方向微分が求められる。 方向微分の値は、勾配ベクトルと速度ベクトルの内積なのだ。 これも最初の微分、全微分、方向微分で説明したのだ。 |
ここからが仰天の話になる。
| 方向微分の式から関数を取り除く |
|---|
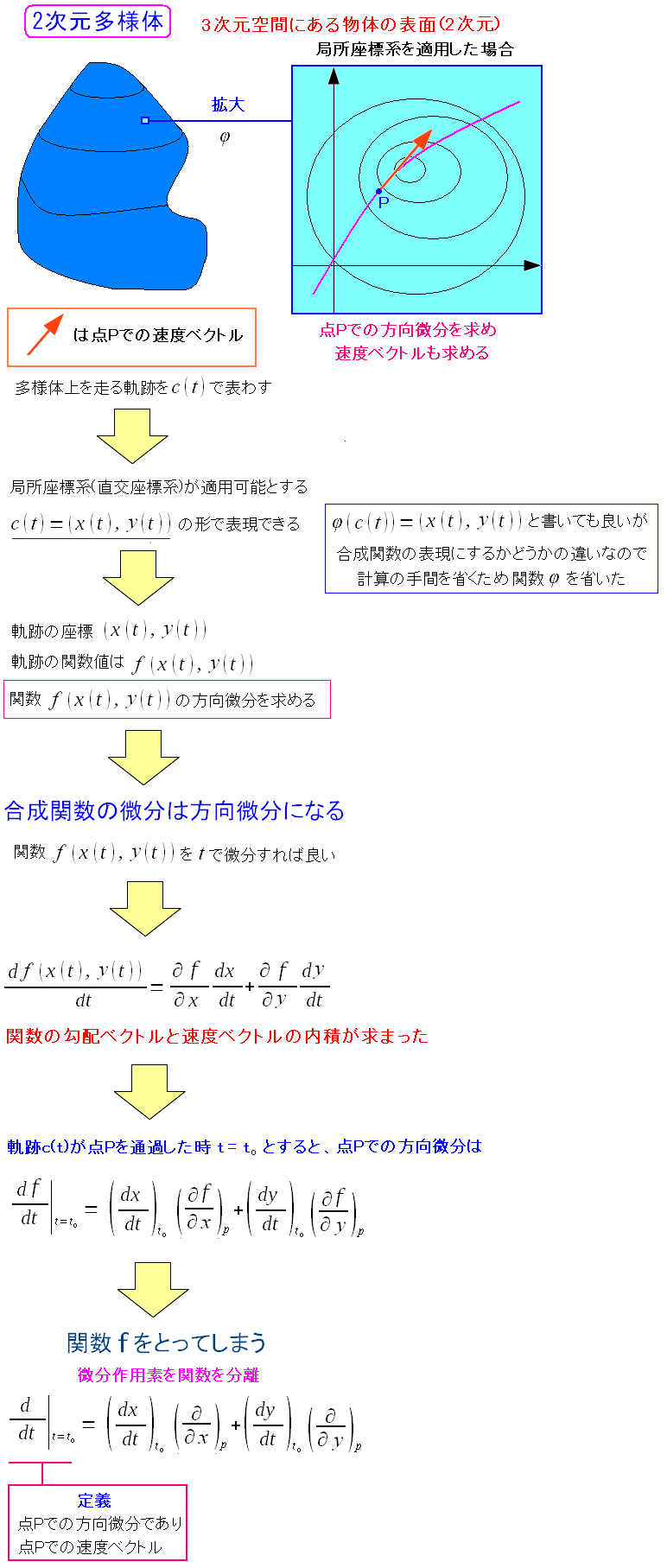 |
|
求めた方向微分の式から、関数fを抜き取ってしまうのだ。 関数fを抜き取った物を、多様体上の方向微分、もしくは速度ベクトルというのだ。 |
微分演算子だけの形にしてしまう
初め、関数を抜き取ってしまう事には衝撃を受けた。
確かに、時間(t)で微分するので、関数から方向微分の値を求める微分演算子ではあるが
これだけだと、何をしたいのか、見えてこない。
少し多様体上の方向微分の式を触ってみる。
すると、またも仰天する事に出くわす。
| 多様体上の方向微分の式を触ってみる |
|---|
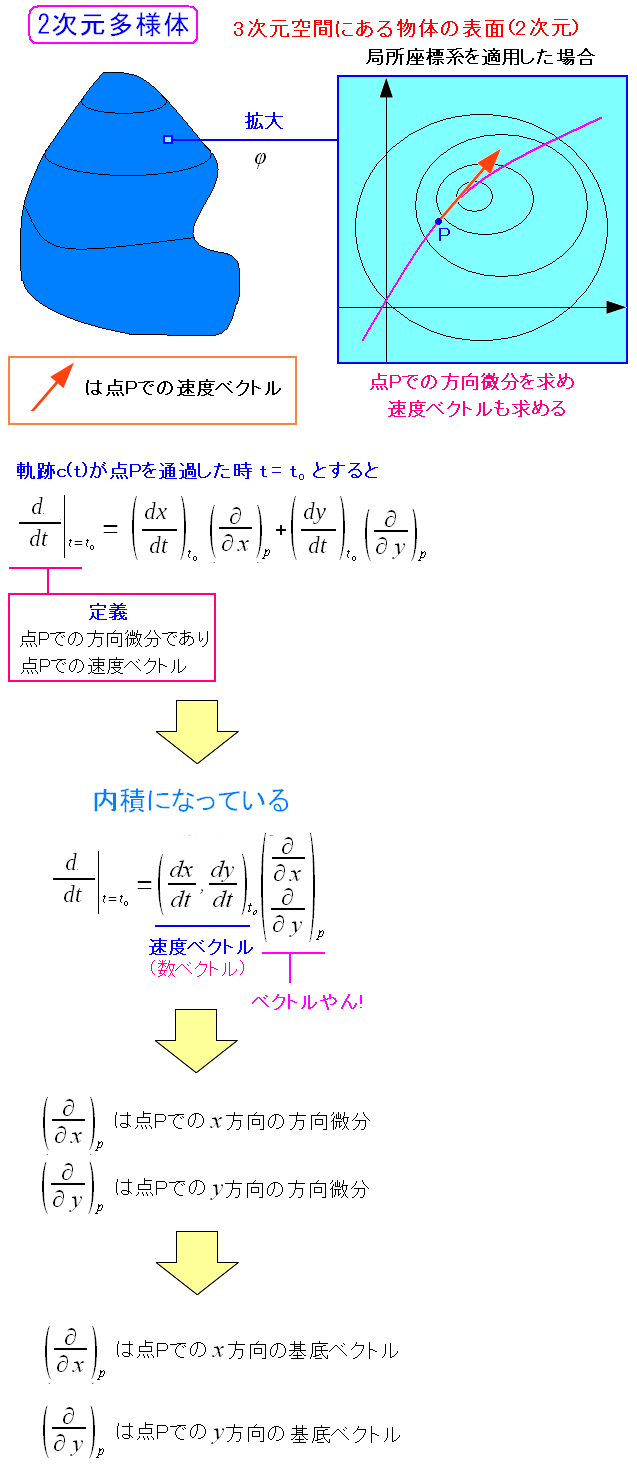 |
|
速度ベクトルと、微分演算子で作るベクトルの内積になっている。 この微分演算子は、各方向の方向微分であり、基底ベクトルでもあるのだ。 |
微分演算子が基底ベクトル!!
まさに衝撃だ。
でも、冷静に考えると納得はできる。
| 速度ベクトルをXY平面(直交座標系)で表わす |
|---|
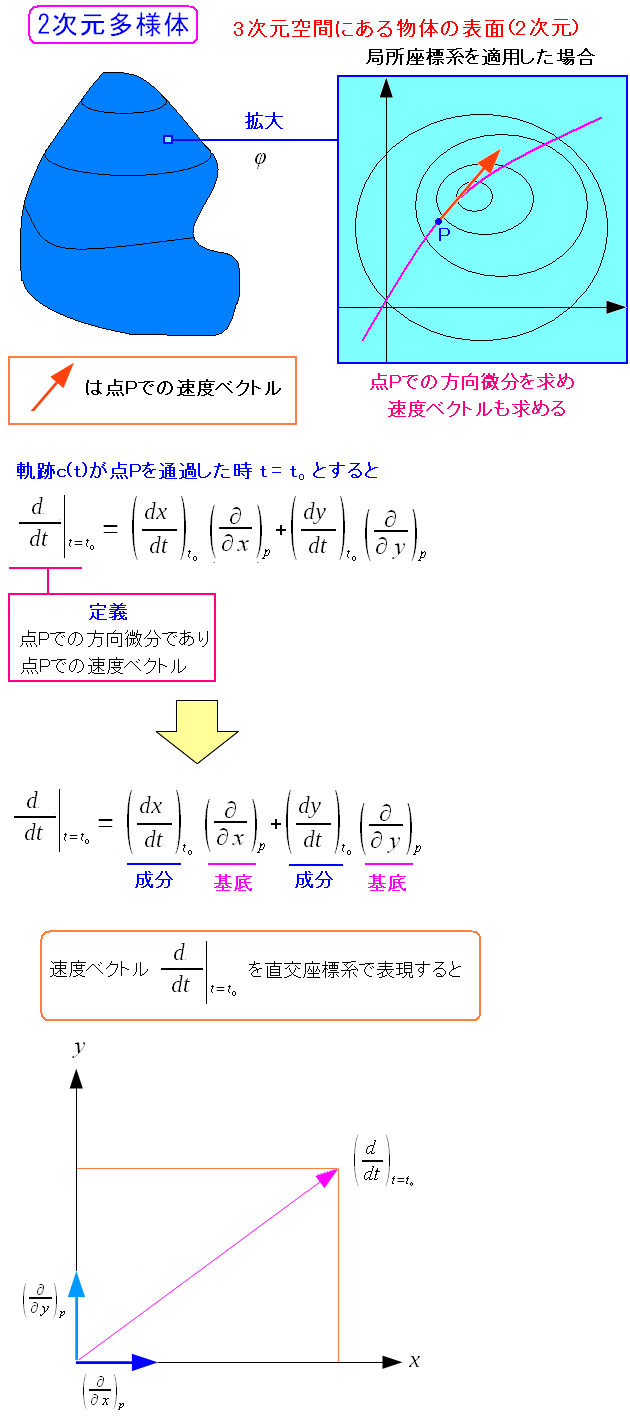 |
|
演算子をベクトルと考えると、非常に見通しが良くなる。 直交座標系での速度ベクトル(数ベクトル)の裏に隠れた基底を使う事で 多様体上の軌跡の速度ベクトルを表現する事ができるのだ。 |
さて、求まった基底ベクトルだが、直交座標系を構成するための
接ベクトル
になる。
| 点Pにおける直交座標系の基底ベクトル |
|---|
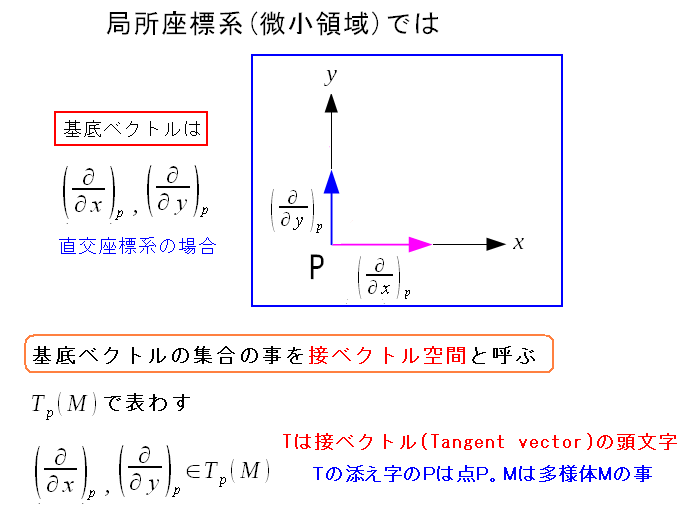 |
|
微分演算子が基底ベクトルなので、違和感がある。 慣れるまでの辛抱なのだ。 |
ところで多様体上で、物事を表現するには
座標系に依存しない形
が求められる。
というわけで、同じ軌跡を使って速度ベクトルを求める場合でも
適用する座標系を極座標系にして見てみる事にした。
あと多様体上の関数に依存しない事も示すため、他の関数を使ってみた。
具体的に、どうやって求めるのかを見てみる。
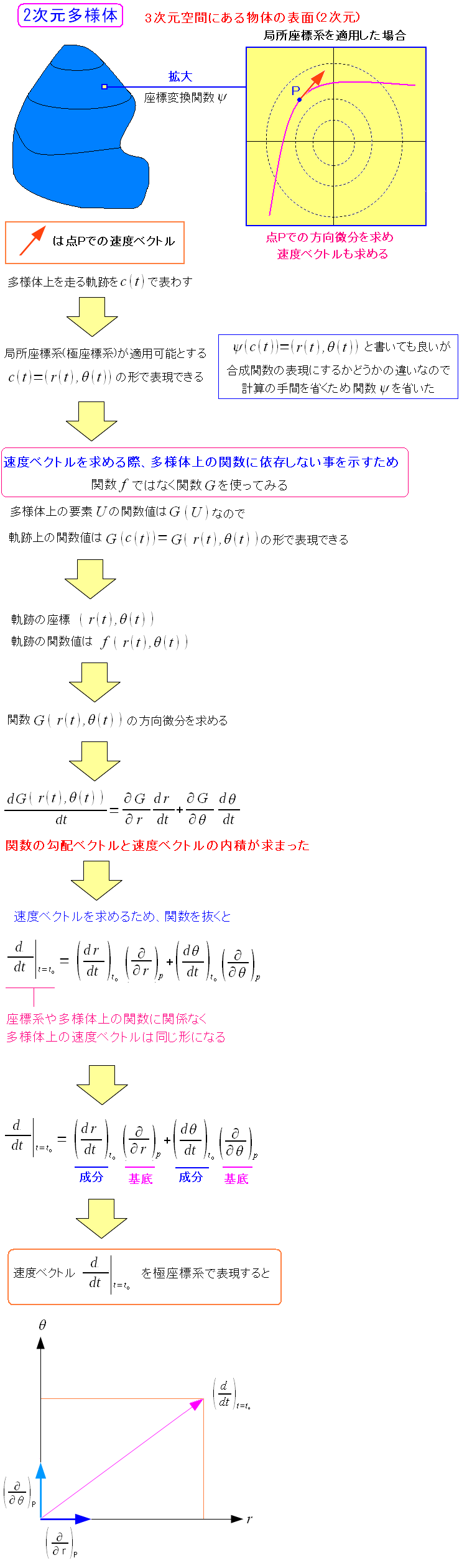
| 極座標系を使って、多様体上の軌跡の速度ベクトルを求めてみた |
|---|
 |
|
直交座標系と同じ形になった。 成分と基底は別物なのだが、単に極座標系で現した場合の表現なのだ。 |
多様体上の速度ベクトルは座標に依存しないが それを構成する要素は座標に依存する。 釈然としないのだが、こういう時は絵を書くとスッキリする。
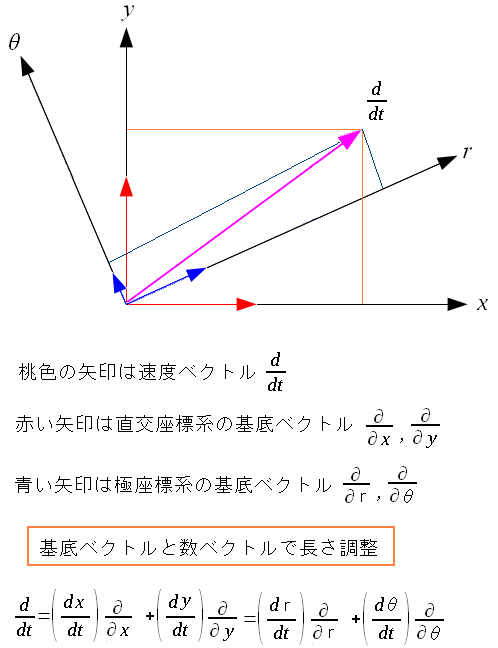
| 速度ベクトルを、各局所座標系でのベクトル表現で表わす |
|---|
 |
|
距離と角度を同じにしているため語弊のある図だが、気にしないで欲しい。 速度ベクトルを構成する、基底ベクトルや、成分(数ベクトル)は 局所座標系によって異なるのだが、それぞれが長さを調整しているため 結果的に同じ物になるのだ。 普段、顔を出している数ベクトルは、座標系を通した形での速度ベクトルだが 裏では基底ベクトルが調整の役割を果たしているのだ。 この後のベクトルの話の所で、共変ベクトルと反変ベクトルを取り上げたのだが まさに、この話になるのだ。 |
数学とは積み重ねの学問。一足飛びでは理解できない。 読む方も大変かもしれないが 書く方も大変なのら-!! 要するに、今まで私が積み重ねていなかっただけに 暗中模索、四苦八苦しながら書いているのが、バレバレなのだ。 さて、3次元の多様体の場合を考えてみる。 適用できる局所座標系を直行座標系にした。
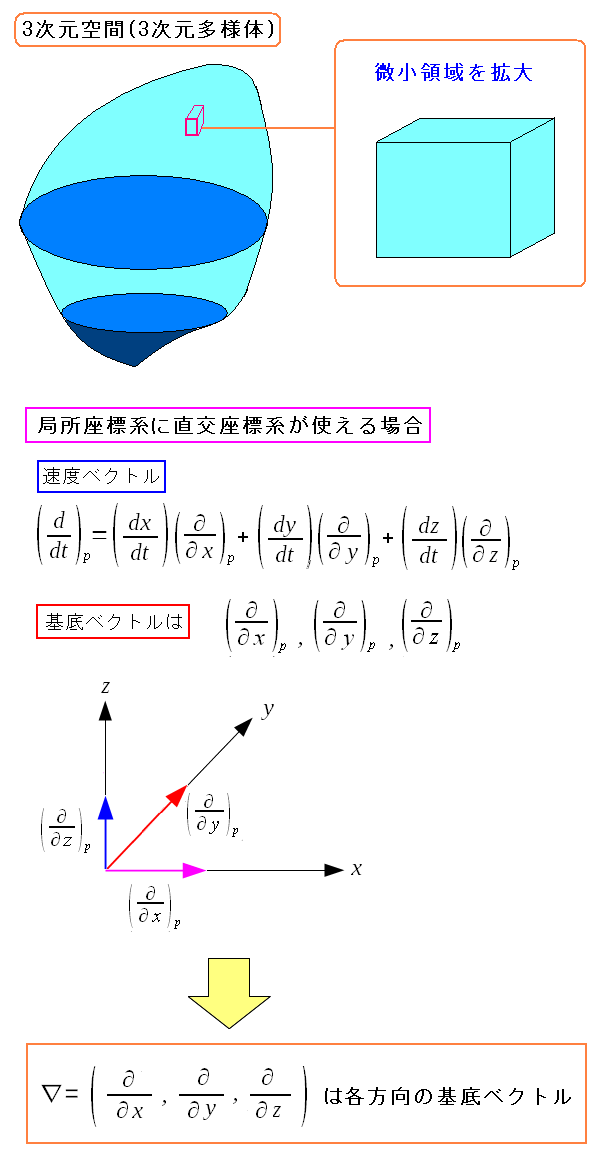
| 3次元の多様体の場合を考えてみる |
|---|
 |
|
適用できる局所座標系を直行座標系にした。 基底ベクトルを並べると、微分演算子の∇(ナブラ)になるのだ。 ∇は接ベクトルで構成されている微分演算子なのだ。 |
∇(ナブラ)の正体が少しづつ見えてきた。
多様体上の関数の全微分
多様体は座標が定めっていないため、座標に依存しない形で 空間を考える分野なのだ。座標に依存しない一般化された形なのだ。 ところで多様体上の関数fを全微分した場合、dfをどう表わすのか? その前に、準備が必要になる。
| M次元多様体からN次元多様体への移す関数をfとする |
|---|
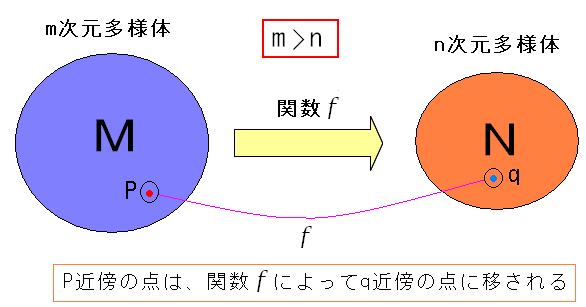 |
| M次元多様体上の点Pを、関数fを使うと、N次元多様体の点qに移動する。 |
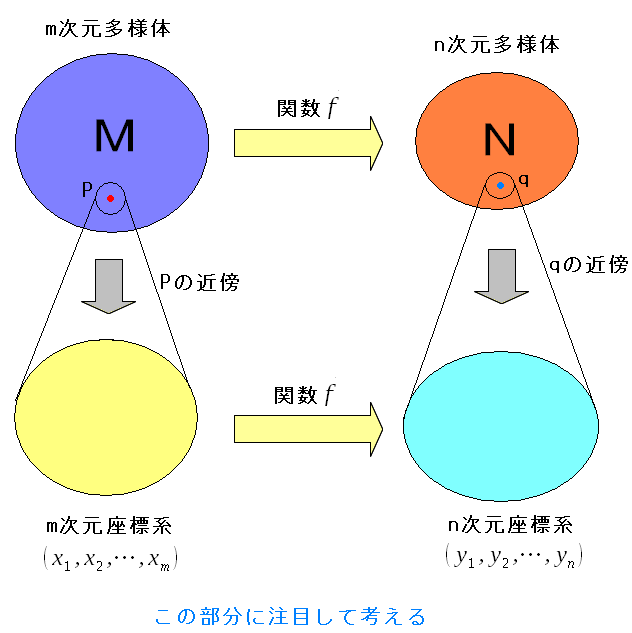
でも、このままでは座標系がないので、前に進まない。 そこで点P付近で使える局所座標系と、点q付近で使える局所座標系を用意する。
| 点P付近で使える局所座標系と、点q付近で使える局所座標系を用意する |
|---|
 |
|
それぞれの点の付近に適用できる局所座標系を用意する。 ところで多様体上の関数fと、関数Fだが、本質的には同じだ。 座標系を適用する前は関数fで、座標系を適用した場合、 関数Fを適用しているだけなのだ。 |
ここでもM次元多様体上の軌跡を使って、巧妙(?)に話をもっていく。
| M次元多様体上の軌跡を活用する |
|---|
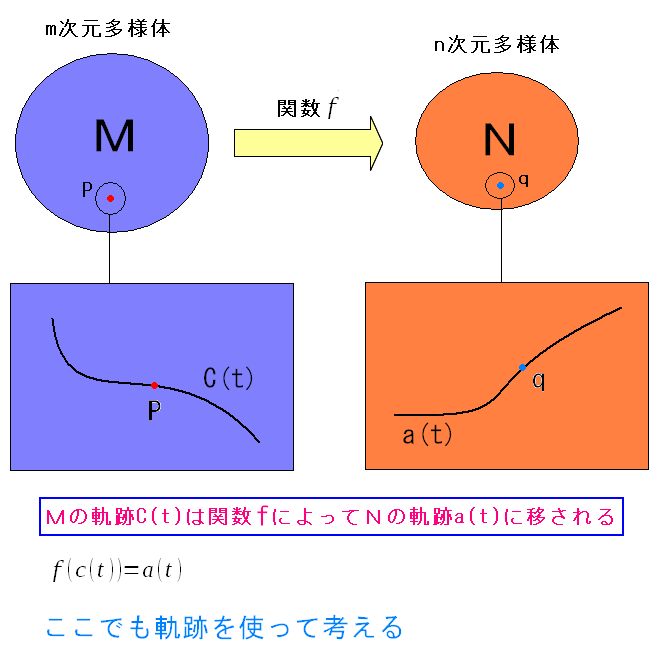 |
| M次元多様体上の軌跡をc(t)としたら、N次元多様体上の軌跡はa(t)=f(c(t))になる。 |
そして、それぞれの速度ベクトルを求める。
| それぞれの速度ベクトルを求める |
|---|
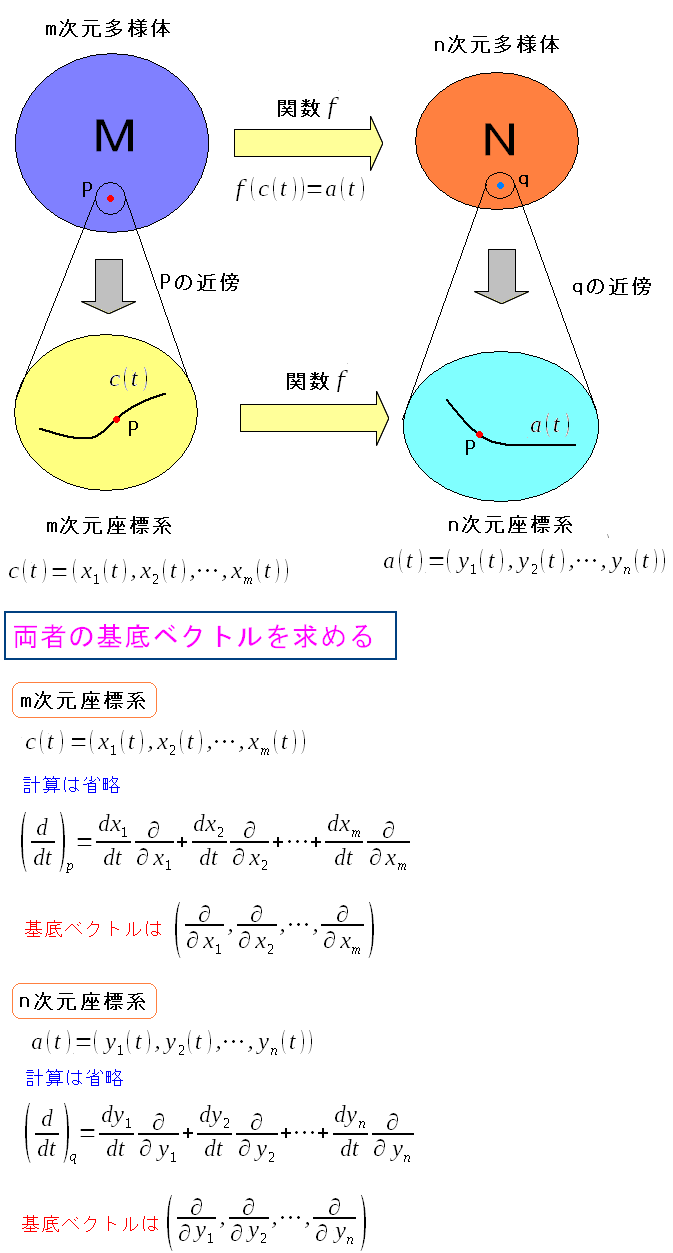 |
| M次元多様体の軌跡c(t)と、N次元多様体の軌跡a(t)の速度ベクトルが求まった。 |
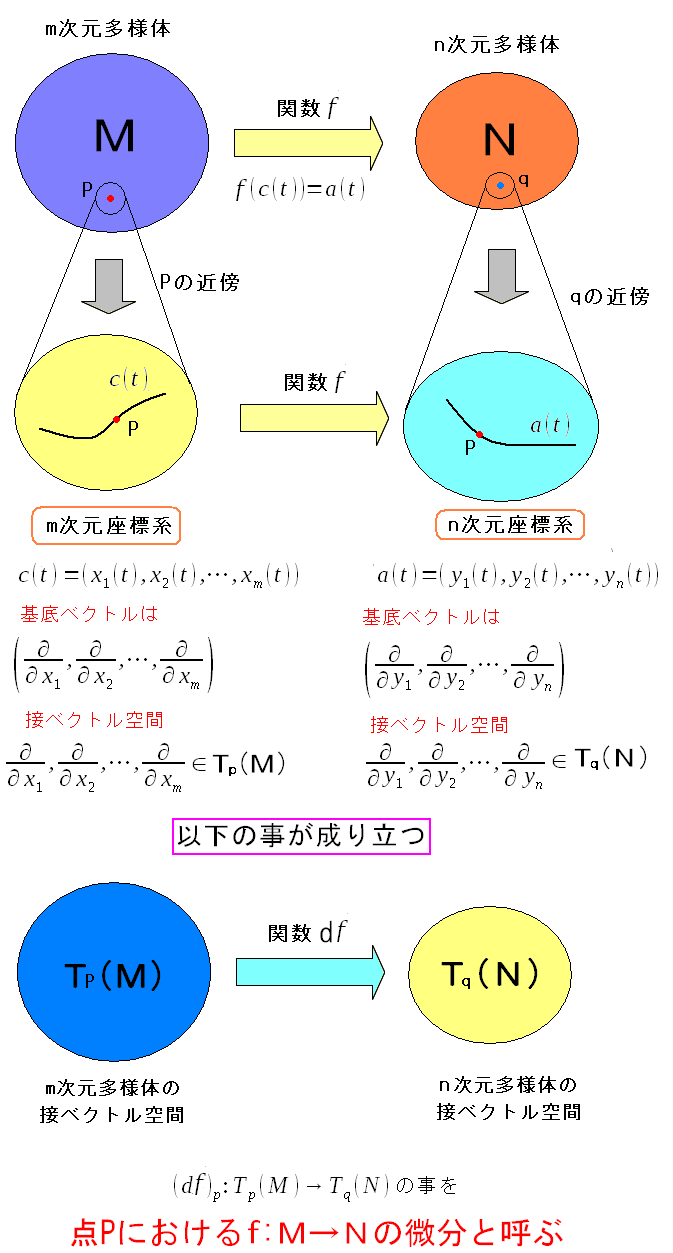
M次元多様体の軌跡と、N次元多様体の軌跡の間には 関数で結ばれている。 速度ベクトル同士はどうなのか。以下のことが成り立つのだ。
| 速度ベクトル同士を結びつける関数 |
|---|
 |
|
M次元多様体からN次元多様体へ移動させる関数fを全微分した物(df)が M次元多様体の速度ベクトルを、N次元多様体の速度ベクトルに移す関数(df)になる。 |
実際に確かめてみるため、まずは次元多様体からN次元多様体へ 移動させる関数fを全微分した物(df)を求めてみる。
| M次元多様体の点からN次元多様体の点へ移動する関数の微分を求める |
|---|
 |
|
関数dfが求まった。行列になっている。 この関数のことをヤコビアンと呼ぶのだ。 |
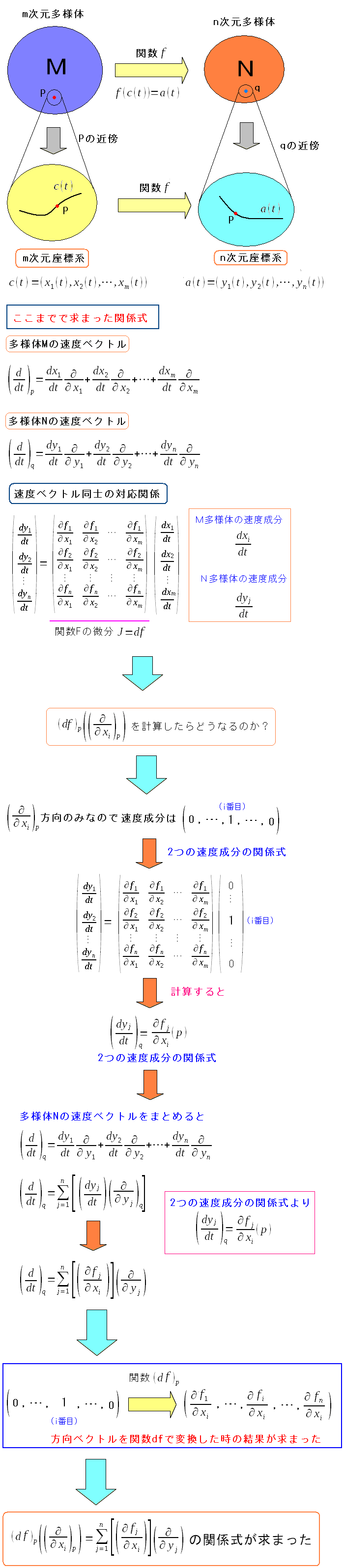
実際に、求まったヤコビアン(df)を使って、M次元多様体の基底ベクトルを N次元多様体の基底ベクトルに変換できるのかどうかを確かめてみる。
| ヤコビアン(df)を使ってみる |
|---|
 |
|
M次元多様体の基底ベクトルの1つを、関数dfで変換すると N次元多様体の基底ベクトルで構成される、ベクトルが求まった。 |
準備完了。 3次元多様体から1次元多様体の場合を考えてみる。
| 3次元多様体から1次元多様体の場合を考えてみる |
|---|
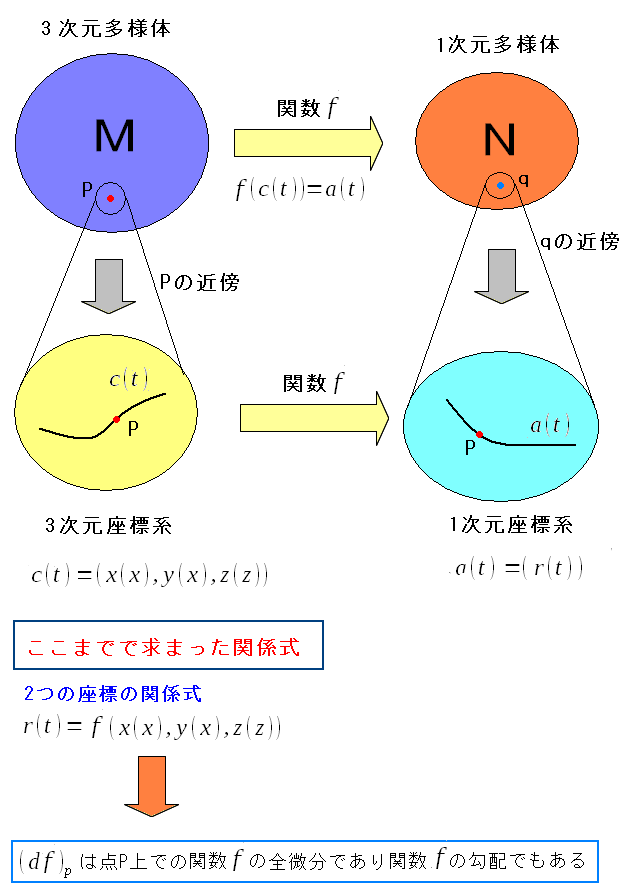 |
| この時、関数fの全微分のdfは、関数fの勾配を表わすものだとわかっている。 |
ここにきて・・・
全微分が座標に依存しない表現方法
というのを知った。驚いた。
でも、よく考えたら、当然の話なのだ。
| 関数値の変化量は座標依存しない |
|---|
|
点Aから点Bまで移動した時の、2点の関数値f(A)、f(B)変化量を考える。 直交座標系だろうが極座標系だろうが、座標に関係なく 点Aの関数値f(A)と、点Bの関数値f(B)は同じなるはず。 そのため関数値の変化量である、f(B)-f(A)も同じになるのだ。 |
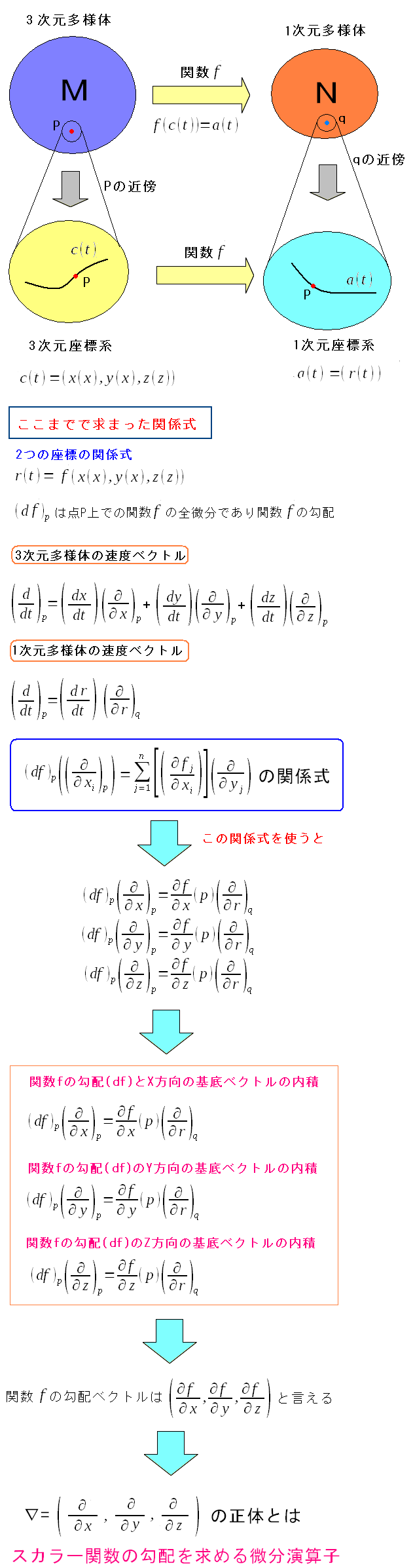
ここで3次元多様体の基底ベクトルを、関数dfで変換してみる。
| 3次元多様体の基底ベクトルを、関数dfで変換してみる |
|---|
 |
|
すると、関数fの勾配ベクトルの成分が出てきたのだ。 同時に∇(ナブラ)の正体も明らかになる。 |
∇(ナブラ)の正体がわかったのだ!!
あっけない結論。ただの微分作用素。
でも、関数の微分だけでなく、ベクトルや行列にも使えるのだ。
それについては後述しています。
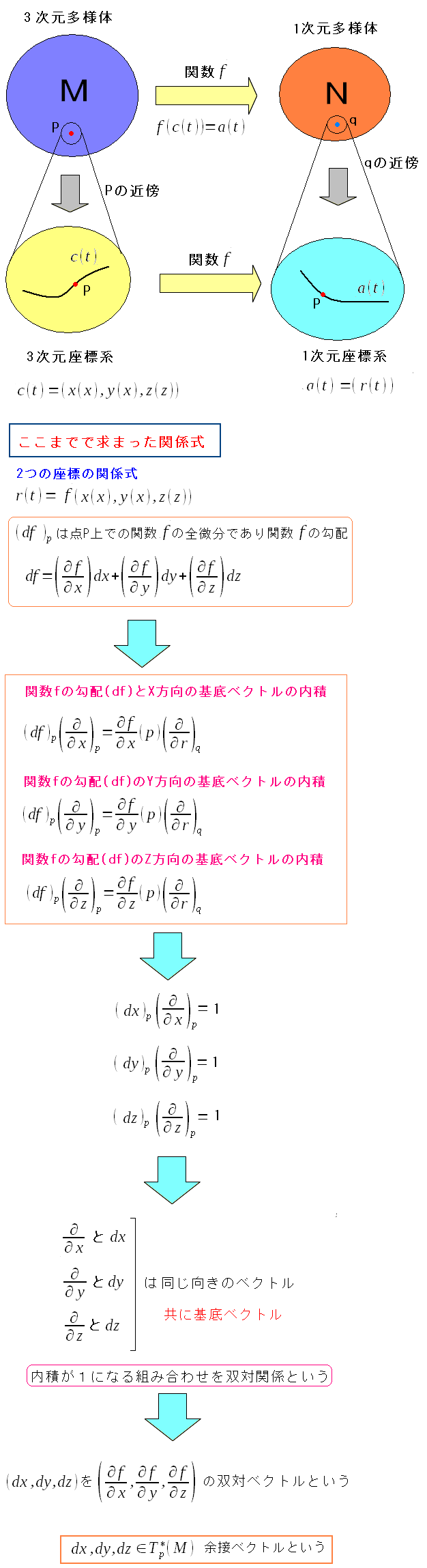
関数fを全微分したdfには話の続きがある。
| dfの基底ベクトルがわかる |
|---|
 |
|
dx,dy,dzが基底ベクトルだというのがわかる。 双対関係については、後で出てきますベクトルの双対関係で触れています。 双対関係から話は、後で出てきます微分形式につながってきます。 |
ところで多様体の目的は
座標系に依存しない一般化した表現
だった。
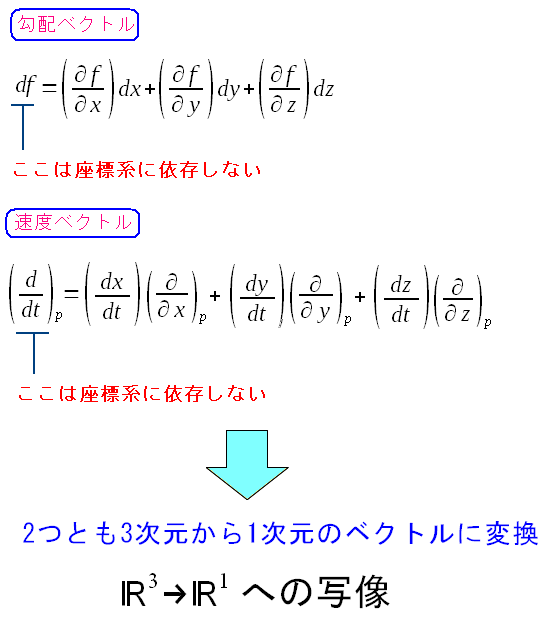
今回は、勾配と速度ベクトルが座標系に依存しない形で表現できた。
| 勾配と速度ベクトルが座標系に依存しない形で表現できた |
|---|
 |
|
勾配も速度ベクトルも、座標系に依存しない形になっている。 数ベクトルだけだと、座標に依存してしまうが 基底ベクトルを用いて表現する事で、座標依存をなくしているのだ。 |
だが、1つ注意が必要だ。
関数の勾配ベクトルは
座標依存しないとは言えない
| 勾配ベクトルは座標依存しないとは言えない |
|---|
|
多様体は長さも何も定義していない空間だ。 そのため「安易に勾配ベクトルが座標依存しないとは言えない」と本に書いていた。 リーマン多様体の話になってくるのだが、そこまで取り上げる気はない。 単に私が、そこまで勉強する馬力がないからだ。 |
座標系に依存しない表現を使う多様体。 はめ込み、埋め込みなどをやっていくと、 メビウスの輪やクラインの壷 の話が出てきたりするのだが、私がそこまで勉強するだけの 労力と時間がないので 興味のある方、勉強してくださいね! で逃げるのだ。 ただ、微分形式という話は行なう。 ∇(ナブラ)の話が、よりわかりやすくなる上、rotやdivの正体がわかる。 そして電磁気の裏に潜んでいる数学の鮮やかさが見えるのが。 微分という名前がついている上、見た目、微分なのだが 実はテンソル積の話なので、テンソル積の説明をしてから 微分形式の説明をするのだ。
電磁気学入門の目次
| 電磁気学入門:目次 | |
|---|---|
| スカラーとベクトル | 簡単なスカラーとベクトルの話です。 ベクトルは方向と大きさを持つ量。方向という量持っているだけに注意が必要です。 |
| 静電気の発見からクーロンの法則 | 今でこそ当たり前の静電気や導体、絶縁体、電荷など どういう経緯で発見し、クーロンの法則まで至ったのかの話です。 |
| クーロン力、電場、近接作用 | 4つの力のうち、クーロン力の位置づけ 電荷が作り出す作用の電場。近接作用の話です。 |
| 微分、全微分、方向微分 | 簡単な微分、全微分、方向微分の話です。 ここをしっかり押さえないと、電磁気の数式の意味が わからなくなります。 |
| ベクトル解析 |
電磁気に必要なベクトル解析の話です。 勾配(grad)、2次元のグリーン定理 ストークスの定理の話です。 |
| 電位ポテンシャル | 電位ポテンシャルです。勾配と電場の関係を使って説明しています。 |
| 電気双極子 |
電気双極子の話です。 物質中で起こる分極を理解するのに必要です。 |
| ガウスの法則 | ガウスの法則の積分形、微分形の話です。 |
| ポアソンの方程式、ラプラス方程式 |
ポアソンの方程式、ラプラス方程式の話です。 単に電荷分布から電位を求めるだけの話にとどまらない 奥が深い分野です。ポテンシャル論、デルタ関数 グリーン関数、固有値問題について触れています。 |
| 静電場と渦なしの法則 |
静電場で、電荷を1周させた時の仕事はゼロ 微分形と微分形の渦なしの法則の話です。 |
| ビオサバールの法則 |
電気と磁場の関係の発見の話から ビオ・サバールの法則が導かれるまでの話です。 |
| 磁気双極子 |
磁気双極子の話で、回転電流になります。 物質中の磁場の話にも関連します。 |
| アンペールの法則 |
アンペールの法則の話です。 積分形・微分形だけでなく、閉回路に流れる電流が作る 磁気双極子の話なども書いています。 |
| ローレンツ力 |
磁場中を移動する電荷にかかる力(ローレンツ力)の話です。 ローレンツ力は相対性理論が絡んでいる事も紹介しています。 |
| ファラデーの誘導起電力の法則 | ファラデーの誘導起電力の話です。 |
| うず電流を使った簡単な物理実験 | 電力計に使われるアラゴの円盤。 そしてIH調理器で熱するために発生させる、うず電流は レンツの法則から電流が発生する原理を応用した物だ。 アラゴの円盤の実験と、IH調理器を使った実験です。 気分転換で読んでください。 |
| ベクトルポテンシャル |
わかりにくいベクトルポテンシャルの話です。 電位は電荷が作る電気のポテンシャルだが ベクトルポテンシャルは電流が作る磁場のポテンシャルの話です。 |
| オームの法則の微分形 | 微小領域でのオームの法則の話です。 |
| マックスウェルの方程式 |
4つのマックスウェルの方程式を書いています。 電場と磁場の変化を図にする事で rotの回転の意味も理解できます。 |
| ゲージ変換 |
ゲージ(gauge)は物差しの意味です。 マックスウェルの方程式をE(電場)とB(磁場)の関係式から φ(電位ポテンシャル)とA(ベクトルポテンシャル)の関係式に 書き換える際、ゲージ変換が使われます。 ゲージ変換の役目を書きました。 |
| 電磁波 |
マックスウェルの方程式から電波が伝わる様子を 視覚的に見てみる話です。 |
| 回転のrotはベクトルの微分 |
ベクトル解析や渦なしの法則で出てくるrotは ベクトルの微分という話です。 |
| 電磁気学の単位系 | 電磁気学の単位系の話です。 物理量の単位系の指数を見る次元解析 電磁気学の歴史と単位系の変遷について触れました。 |
| 電気泥棒:電気と法律の話 |
電気は物体なのか、無形物なのか。 明治時代に、電気を無断で使った場合、物か、そうでないかで 窃盗罪になるかどうかが裁判で問われました。 ちょっとした科学と法律の話です。気分転換で読んでください。 |
| 数ベクトルと基底ベクトル | ベクトルの話です。 矢印だけがベクトルでない事。 数ベクトルと基底ベクトルの違いの話です。 多様体、反変・共変ベクトルを理解するのに必要です |
| 多様体 | 空間を一般化した話です。 ▽(ナブラ)の正体に迫まります |
| 外積代数 |
外積、テンソルについて書いています。 極性ベクトル、軸性ベクトル 外積は行列で、ベクトルは見せかけの姿だった話です。 |
| ベクトルの双対関係 |
反変ベクトル、共変ベクトル、双対関係 ベクトル解析、外積代数の話 外積、テンソルについて書いています。 |
| ローレンツ力と相対性理論 |
磁場は電場の相対論的効果だった話です。 ローレンツ力を使って、導線が作る磁場を使って説明です。 |
| 微分形式 |
多様体の話の続きです。 座標に依存しない形での関数やベクトルの微分の話です。 ガウスの法則、アンペールの法則、マックスウェルの方程式が 鮮やかな形で表現できます。 ∇(ナブラ)の正体もわかります。 |
| 物理と対称性 |
マックスウェルの方程式をよく見ると対称性があります。 物理の方程式と対称性を数学的な観点でみると 意外なつながりがあるという話です。 |
| マックスウェルの応力 |
電気力線を弾性体(ゴム)とみなして、力の伝わり方などを 説明した考え方です。 |
| 電場エネルギー | 電場が持つエネルギーの式を導いた話です。 |
| 磁場エネルギー |
磁場が持つエネルギーの式です。 手抜きの説明と、直流RL回路を使った説明を書きました。 |
| ポインティングベクトル |
電磁エネルギーの流れ「ポインティングベクトル」の話です。 電磁波でもエネルギー保存則が成り立つ話から ポインティングベクトルを導いています。 |
| 電気エネルギーは導線の外を伝わる |
導線の外を電気エネルギーが流れる話です。 私が誤解した事、その誤解を解いていく過程を紹介しながら 「目からウロコ」にたどり着いた話です。 |
| 物質中の電場 | 物質中の電場の話です。 分極の話をしながら、物質中の電場の話をします |
| 物質中の磁場 | 磁性の話をしながら、物質中の磁場の話をします |
| 物質中のマックスウェルの方程式 | 物質中でもマックスウェルの方程式が成り立つ話です。 |
| 導体に侵入する電磁波 |
導体に侵入する電磁波が減衰していく話です。 表皮効果と同じ「表皮の厚さ」が出てきます |
| 表皮効果 |
目的の表皮効果の話です。 マックスウェルの方程式を解きながら 交流電流の周波数を上げると、表面にしか電流が流れなくなる話です。 |