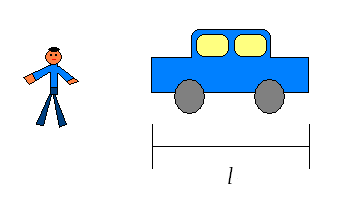
人も車も動いていない場合、車の長さは変わらない。
システム奮闘記:その105
(2016年5月22日に掲載)
磁場の正体は電場
ローレンツ力の所を勉強していると、直面した疑問があった。 磁場中に、荷電粒子が止まっている時、何も力が働かないが 荷電粒子が動いていると、ローレンツ力という力が働く。 調べてみると、以下のサイトを発見した。 特殊相対論と磁場(東海大学) 磁場は電場の相対論的効果 というのだ。 簡単にいえば 磁場は電場だった!! というのだ。 衝撃の内容だった。 そもそも磁場は、電場だった事なんて 全く知らへんかった!! のだ。 学生時代、相対性理論は習っていないので そんなの知るわけあらへんと開き直る。 なぜ磁場は、電場の相対論的効果なのか。 だが、それを知るには、相対性理論の知識が必要だ。ローレンツ収縮
まずはローレンツ収縮の話だ。
| 人と車があるとする |
|---|
 |
|
車の長さを「l」とする。 人も車も動いていない場合、車の長さは変わらない。 |
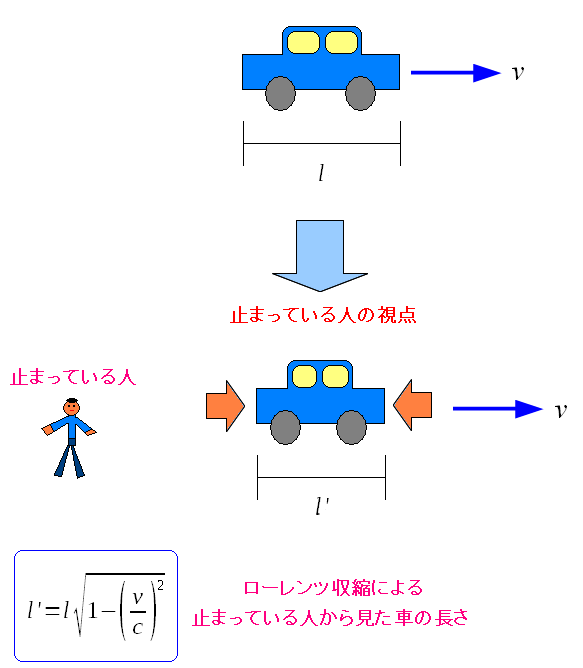
ローレンツ収縮とは、動いている物体の長さが縮むという現象なのだ。
| ローレンツ収縮とは、動いている物体の長さが縮むという現象 |
|---|
 |
|
走る物体(車)を、止まっている人から見ると、車の長さが縮む。 この現象をローレンツ収縮というのだ。 とても信じがたい話だ。 ただ、縮む長さが、時速100Kmでも、1000Kmであっても 小さすぎる量なので、精密な定規を使っても、わからないぐらいだ。 光速に近づかないと、縮んで見えないのだ。 ところで光の速度は3.0×10^8m/sで、一定なのだ。 そのためニュートン力学では説明できない事が出てくる。 光の速度で走る物体から物を投げたら、物の速度はどうなるのか等だ。 その辺りの矛盾を解決したのが特殊相対性理論なのだ。 |
ローレンツ収縮の式を導くには、マイケルソン・モーレーの実験をはじめ 色々な話を知る必要があるのだが・・・ 特殊相対性理論の勉強するのが大変なので 名誉なき撤退。つまり、ただの脱走をする と宣言して、逃げる事にした。 私が力尽きるまで相対性理論を勉強して、それを説明したとしても トンデモ科学になっては良くない、労力と時間の無駄だ。 ところで相対性理論は難しい。どれくらい難しいのか? 専門家でも正しく理解してへん人がおる というぐらいだ。 相対論・宇宙論が専門で神戸大学名誉教授の松田卓也さんのコラムがある。 専門家でも惑わす相対性理論の罠(受験生のためのポータルサイト 大学ジャーナル) 相対性理論の専門家の大学のさんですら正しく理解していない人がいる話。 専門家でもワナにハマるのは、ちょっと信じがたい話なのだが、それぐらい難解な理論だというのだ。
アンペールの法則と相対性理論
東海大学の資料では、導線を流れている電流が作る磁場の正体は 電場という話なのだ。 なので、東海大学の資料を丸写しした説明を載せる事にした。 さて、導線を流れる電流が作る磁場は、アンペールの法則により 求める事ができた。
| 導線を流れる電流が作る磁場 |
|---|
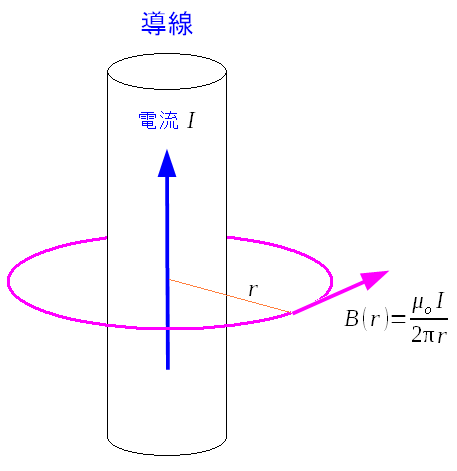 |
| ここで行なうのは、磁場は電場であることを示す事なのだ。 |
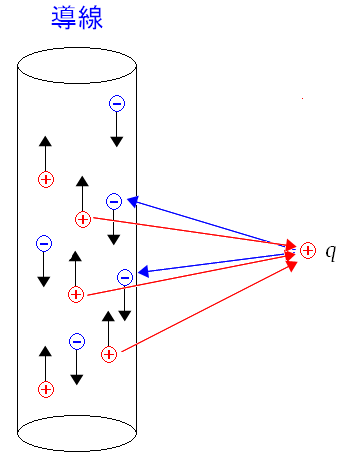
さて、導線の中に電流が流れている時、導線内部の正の電荷と 負の電荷は反対方向に進んでいる。 導線から距離rの位置に電荷qがあるとする。
| 導線内部の正の電荷と負の電荷は反対方向に進んでいる |
|---|
 |
|
電荷qは、導線内の正電荷と負電荷からクーロン力を受けている。 東海大学の資料の丸写し |
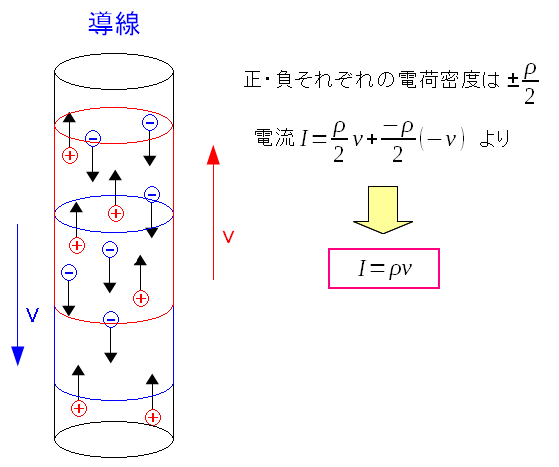
導線内部の電流を、電荷密度で表わすと以下のようになる。
| 導線内部の電流を、電荷密度で表わす |
|---|
 |
|
電流とは、任意の切り口を、1秒間に流れる電荷量だ。 なので、電荷密度×速度となり、ρ×vになる。 東海大学の資料の丸写し |
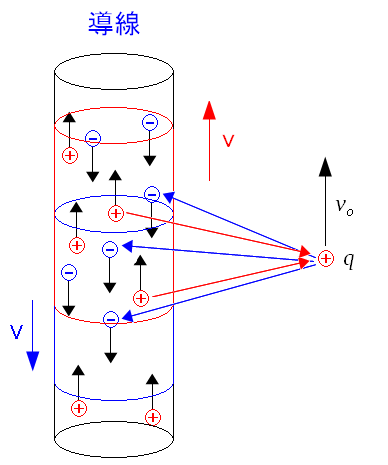
もし導線から距離r離れた位置にある電荷qが 速度voで動いているとする。
| 導線から距離r離れた位置にある電荷qが速度voで動いている |
|---|
 |
|
導線から距離r離れた位置にある電荷qが速度voで動いている場合 ローレンツ収縮は起こるのだろうか? 東海大学の資料の丸写し |
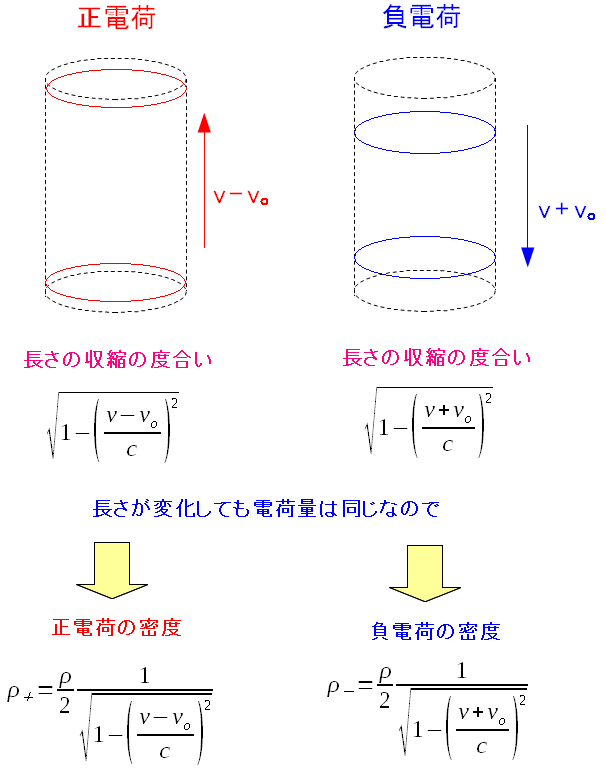
導線内を流れる正電荷と負電荷の部分での ローレンツ収縮を見てみる。
| 導線内を流れる正電荷と負電荷の部分でのローレンツ収縮 |
|---|
 |
|
正電荷も負電荷もローレンツ収縮は起こる。 電荷量は同じだが、ローレンツ収縮によって、電荷がある領域が縮むため 電荷密度が変化するのだ。 東海大学の資料の丸写し |
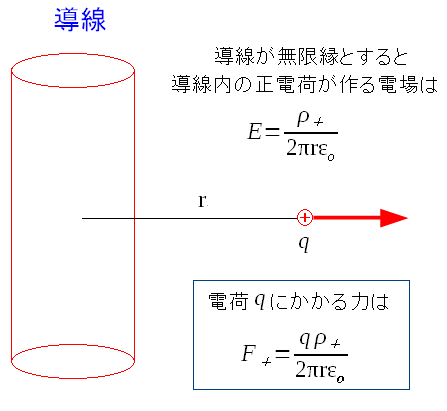
導線内の正電荷が、電荷qに与える力を求めてみる。
| 導線内の正電荷が、電荷qに与える力を求める |
|---|
 |
|
導線が無限に長いと仮定して、電荷qにかかる力を求める。 東海大学の資料の丸写し |
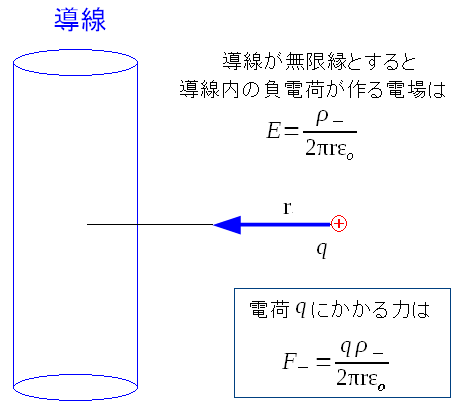
次に導線内の正電荷が、電荷qに与える力を求めてみる。
| 導線内の負電荷が、電荷qに与える力を求める |
|---|
 |
|
導線が無限に長いと仮定して、電荷qにかかる力を求める。 東海大学の資料の丸写し |
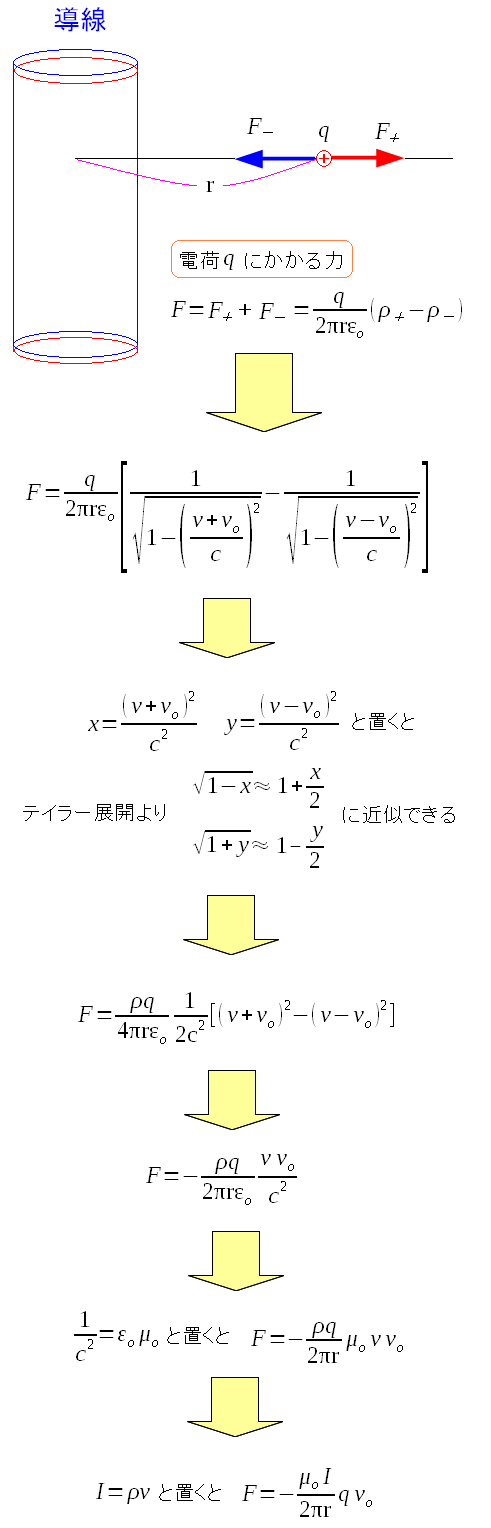
正電荷と負電荷が、電荷qに与える力を足し合わせると、 導線内の電荷が与える力が求まる。
| 正電荷と負電荷が、電荷qに与える力を足し合わせる |
|---|
 |
|
何やら、見た事のあるような式が導かれる。 東海大学の資料の丸写し |
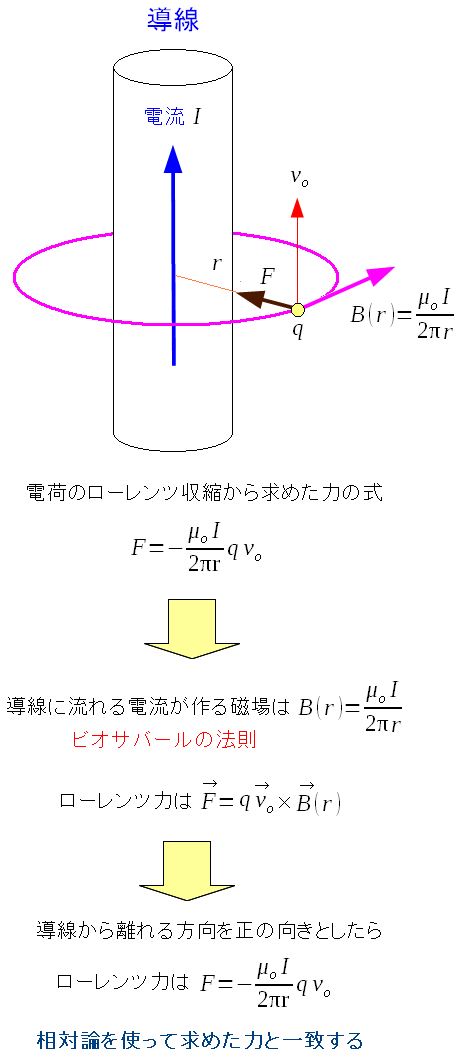
無限に長い導線に流れる電流が作る磁場と、 その磁場中を動く電荷qに働くローレンツ力とを比較してみる。
| 電流を流れる電荷が与える力と 磁場によるローレンツ力とを比較してみる。 |
|---|
 |
|
見事に一致する。 磁場は、電場の相対論的効果だと言えるのだ。 東海大学の資料の丸写し |
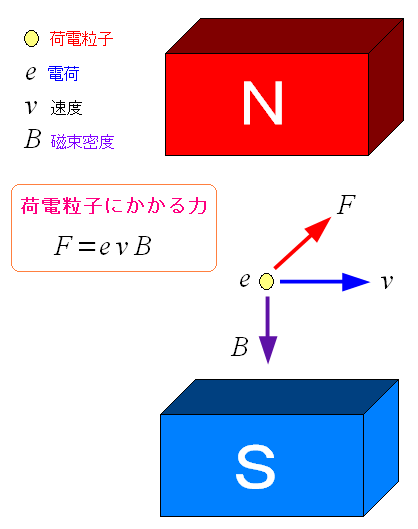
磁場は、電場の相対論的効果 というのを物理の説明で納得できた。 それにしても「東海大学の資料の丸写し」を連発したのだ。 でも、私は恥ずかしい行為とは思っていない。 丸写しを隠して、いかにも自分が作ったように見せかけるのが、恥ずべき行為であって 正直に「自力では作成できへんから、丸写しさせていただいた」を表明するのは 恥ずかしい行為でも何でもない。正直さを表明しているのだ!!! あとでわかった話。ファインマンの物理の本にも同じような説明が書いていた。 東海大学の資料ではなく、最初にファインマンの本を見ていたら ファインマンの説明を丸写ししていたと思う。 磁石の中を電荷が動いた場合、ローレンツ力が働く。 この場合は、どう考えるのか?
| 磁石の中を電荷が動いた場合、ローレンツ力が働く |
|---|
 |
|
東海大学の資料の説明で、電流が作る磁場は、電場だったのがわかったが 磁石の磁場も、同様に、電場由来なのか。 そうだとしたら、その電場はどこで発生しているのか? |
色々、調べてみたが わかりやすい物を探しても 見つからへん!! なのだ。 そのため知りたい人は 勉強してください と発言をして、逃げる事にしたのだ。
電磁気学入門の目次
| 電磁気学入門:目次 | |
|---|---|
| スカラーとベクトル | 簡単なスカラーとベクトルの話です。 ベクトルは方向と大きさを持つ量。方向という量持っているだけに注意が必要です。 |
| 静電気の発見からクーロンの法則 | 今でこそ当たり前の静電気や導体、絶縁体、電荷など どういう経緯で発見し、クーロンの法則まで至ったのかの話です。 |
| クーロン力、電場、近接作用 | 4つの力のうち、クーロン力の位置づけ 電荷が作り出す作用の電場。近接作用の話です。 |
| 微分、全微分、方向微分 | 簡単な微分、全微分、方向微分の話です。 ここをしっかり押さえないと、電磁気の数式の意味が わからなくなります。 |
| ベクトル解析 |
電磁気に必要なベクトル解析の話です。 勾配(grad)、2次元のグリーン定理 ストークスの定理の話です。 |
| 電位ポテンシャル | 電位ポテンシャルです。勾配と電場の関係を使って説明しています。 |
| 電気双極子 |
電気双極子の話です。 物質中で起こる分極を理解するのに必要です。 |
| ガウスの法則 | ガウスの法則の積分形、微分形の話です。 |
| ポアソンの方程式、ラプラス方程式 |
ポアソンの方程式、ラプラス方程式の話です。 単に電荷分布から電位を求めるだけの話にとどまらない 奥が深い分野です。ポテンシャル論、デルタ関数 グリーン関数、固有値問題について触れています。 |
| 静電場と渦なしの法則 |
静電場で、電荷を1周させた時の仕事はゼロ 微分形と微分形の渦なしの法則の話です。 |
| ビオサバールの法則 |
電気と磁場の関係の発見の話から ビオ・サバールの法則が導かれるまでの話です。 |
| 磁気双極子 |
磁気双極子の話で、回転電流になります。 物質中の磁場の話にも関連します。 |
| アンペールの法則 |
アンペールの法則の話です。 積分形・微分形だけでなく、閉回路に流れる電流が作る 磁気双極子の話なども書いています。 |
| ローレンツ力 |
磁場中を移動する電荷にかかる力(ローレンツ力)の話です。 ローレンツ力は相対性理論が絡んでいる事も紹介しています。 |
| ファラデーの誘導起電力の法則 | ファラデーの誘導起電力の話です。 |
| うず電流を使った簡単な物理実験 | 電力計に使われるアラゴの円盤。 そしてIH調理器で熱するために発生させる、うず電流は レンツの法則から電流が発生する原理を応用した物だ。 アラゴの円盤の実験と、IH調理器を使った実験です。 気分転換で読んでください。 |
| ベクトルポテンシャル |
わかりにくいベクトルポテンシャルの話です。 電位は電荷が作る電気のポテンシャルだが ベクトルポテンシャルは電流が作る磁場のポテンシャルの話です。 |
| オームの法則の微分形 | 微小領域でのオームの法則の話です。 |
| マックスウェルの方程式 |
4つのマックスウェルの方程式を書いています。 電場と磁場の変化を図にする事で rotの回転の意味も理解できます。 |
| ゲージ変換 |
ゲージ(gauge)は物差しの意味です。 マックスウェルの方程式をE(電場)とB(磁場)の関係式から φ(電位ポテンシャル)とA(ベクトルポテンシャル)の関係式に 書き換える際、ゲージ変換が使われます。 ゲージ変換の役目を書きました。 |
| 電磁波 |
マックスウェルの方程式から電波が伝わる様子を 視覚的に見てみる話です。 |
| 回転のrotはベクトルの微分 |
ベクトル解析や渦なしの法則で出てくるrotは ベクトルの微分という話です。 |
| 電磁気学の単位系 | 電磁気学の単位系の話です。 物理量の単位系の指数を見る次元解析 電磁気学の歴史と単位系の変遷について触れました。 |
| 電気泥棒:電気と法律の話 |
電気は物体なのか、無形物なのか。 明治時代に、電気を無断で使った場合、物か、そうでないかで 窃盗罪になるかどうかが裁判で問われました。 ちょっとした科学と法律の話です。気分転換で読んでください。 |
| 数ベクトルと基底ベクトル | ベクトルの話です。 矢印だけがベクトルでない事。 数ベクトルと基底ベクトルの違いの話です。 多様体、反変・共変ベクトルを理解するのに必要です |
| 多様体 | 空間を一般化した話です。 ▽(ナブラ)の正体に迫まります |
| 外積代数 |
外積、テンソルについて書いています。 極性ベクトル、軸性ベクトル 外積は行列で、ベクトルは見せかけの姿だった話です。 |
| ベクトルの双対関係 |
反変ベクトル、共変ベクトル、双対関係 ベクトル解析、外積代数の話 外積、テンソルについて書いています。 |
| ローレンツ力と相対性理論 |
磁場は電場の相対論的効果だった話です。 ローレンツ力を使って、導線が作る磁場を使って説明です。 |
| 微分形式 |
多様体の話の続きです。 座標に依存しない形での関数やベクトルの微分の話です。 ガウスの法則、アンペールの法則、マックスウェルの方程式が 鮮やかな形で表現できます。 ∇(ナブラ)の正体もわかります。 |
| 物理と対称性 |
マックスウェルの方程式をよく見ると対称性があります。 物理の方程式と対称性を数学的な観点でみると 意外なつながりがあるという話です。 |
| マックスウェルの応力 |
電気力線を弾性体(ゴム)とみなして、力の伝わり方などを 説明した考え方です。 |
| 電場エネルギー | 電場が持つエネルギーの式を導いた話です。 |
| 磁場エネルギー |
磁場が持つエネルギーの式です。 手抜きの説明と、直流RL回路を使った説明を書きました。 |
| ポインティングベクトル |
電磁エネルギーの流れ「ポインティングベクトル」の話です。 電磁波でもエネルギー保存則が成り立つ話から ポインティングベクトルを導いています。 |
| 電気エネルギーは導線の外を伝わる |
導線の外を電気エネルギーが流れる話です。 私が誤解した事、その誤解を解いていく過程を紹介しながら 「目からウロコ」にたどり着いた話です。 |
| 物質中の電場 | 物質中の電場の話です。 分極の話をしながら、物質中の電場の話をします |
| 物質中の磁場 | 磁性の話をしながら、物質中の磁場の話をします |
| 物質中のマックスウェルの方程式 | 物質中でもマックスウェルの方程式が成り立つ話です。 |
| 導体に侵入する電磁波 |
導体に侵入する電磁波が減衰していく話です。 表皮効果と同じ「表皮の厚さ」が出てきます |
| 表皮効果 |
目的の表皮効果の話です。 マックスウェルの方程式を解きながら 交流電流の周波数を上げると、表面にしか電流が流れなくなる話です。 |