システム奮闘記：その105

電磁気の単位系

(2016年5月22日に掲載)

CGS単位系とMSKA単位系

　物理量を表わす単位系にはいくつかあるのだが
主に使われているのがMKSA有理単位系だ。

MKSA有理単位系
M	メートルの略で、長さの単位系を表わす。
K	キログラムの略で、質量の単位系を表わす
S	Second(秒)の略で、時間の単位系を表わす。
A	アンペアの略で、電流の単位系を表わす。


　他にもCGS単位系がある。

CGS単位系
C	センチメートルの略で、長さの単位系を表わす。
G	グラムの略で、質量の単位系を表わす
S	Second(秒)の略で、時間の単位系を表わす。


　電磁気では、主にMKSA有理単位系を使われるが、分野や先生によっては
CGS単位系を使う場合があるので、物理量を見る際は単位系に注意が必要だ。


次元解析

　さて、電荷とか磁場といった物理量が、どんな単位系で構成されているのか。
それを知る方法として次元解析がある。

　次元解析は、高校の物理でも少し触れるみたいだし
力学でも出てくるのだが・・・

　私自身が忘れてしまった!!

　なので、取り上げる事にした。

　次元といっても、縦・横・高さの3次元といった空間の話ではない。


　次元解析とは、物理量を構成する単位系の指数で表わすことだ。

物理量は長さ・質量・時間・電流で表わせる

物理量は長さ・質量・時間・電流で表わせるのだ。よく電流を意味する「I」が出てくるのだが、調べてみると「Intensity」のようだ。「current intensity」(流れの強さ)に由来している。とwikipediaの英語版には書いていた。「流れの強さ」の意味なので、なんとなく、わかった感じにはなる。


　これだと、いまいち、よくわからない。
　そこで具体例を見てみる。

速度、運動量、運動エネルギーを次元解析

次元解析によって、物理量が、どういう形で基本4つの単位系で構成されているのかがわかる。次元を調べることによって、同じ物理量か異なる物なのかの判別が可能になる。


　そして電磁気学量のMKSA有理単位系の次元解析は以下のようになる。

電磁気学量のMKSA有理単位系の次元解析

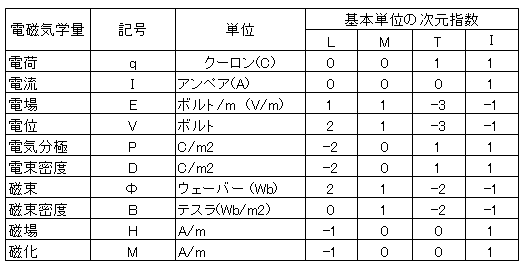今まで出てきた電場とか磁場の単位の構成要素や指数がわかる。


　物理量と単位と次元の指数を比較すれば、計算で求めた式の
物理量が正しいのか確認するのに使える。

　例としてローレンツ力は、本当に力の次元だろうか?
　電荷や磁束密度があるから、本当に力の物理量なのか確かめてみたくなる。

　そこで次元解析をしてみる。

ローレンツ力の式を次元解析

電荷×速度×磁束密度の次元が、力の次元と一致する。ローレンツ力が「力」という物理量を持っている事がわかる。


　電磁気に限らず、物理の式で出てきた物が、物理量として、
本当に正しいかどうかのか確かめる手段として
次元解析があるのだ。


電磁気学の単位系の変遷

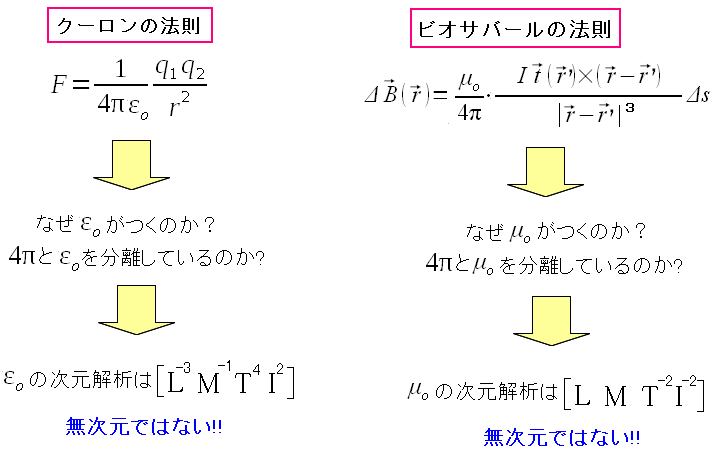
　ところでクローン力やビオサバールの法則には、誘電率や透磁率という
係数があるのか？
　そして、それらは次元を持っている。

クローン力やビオサバールの法則の式についての疑問

クーロンの法則の式にある誘電率だが、分母になっている。そして4πと分離された形になっている。ビオサバールの法則の式にある透磁率だが、分子になっている。 4πと分離された形になっている。両方とも物理量を持っている。


　もちろん・・・

　今まで考えた事、あらへん!!

　なのだ。
　そこで調べてみると、以下の資料が見つかった。

　電磁気学の単位系が難しい理由
　電磁場の単位系と法則(名古屋大学:PDF)

　見ていくと・・・

　電磁気学の歴史が垣間見える

　のだ。

静電単位系(CGSesu単位系)

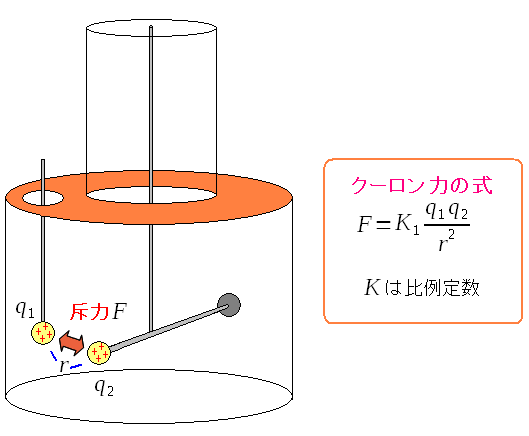
　クーロン力の発見の所でも書いたが、当時は電荷の物理量はなかった(単位もない)
　ただ、距離の2乗に反比例している事や電荷量の積に比例する事はわかった。

クーロン力の発見当初の式

電荷の積に比例している事と、距離の2乗に反比例している事がわかっていた。そこで比例定数を「K1」と置いたのだ。


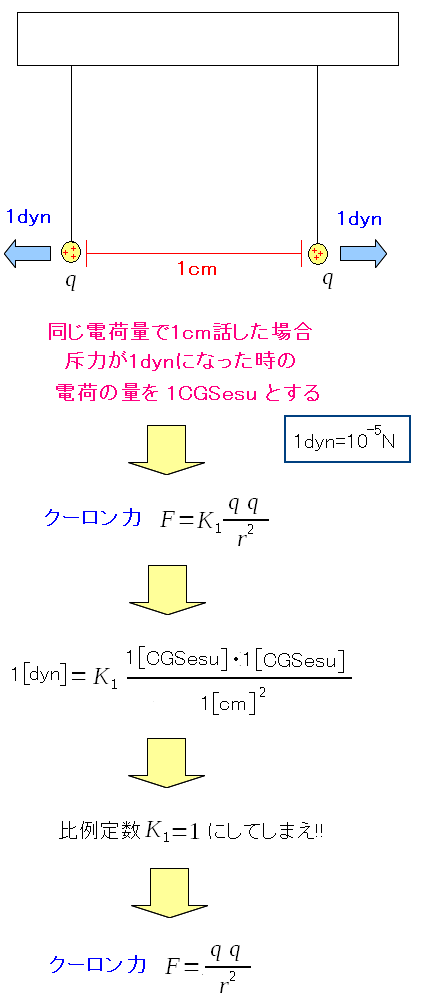
　電荷の単位は決まっていない。
　そこで以下の決まりごとを作った。

クーロン力の式と、電荷量の定義(CGSesu単位系)

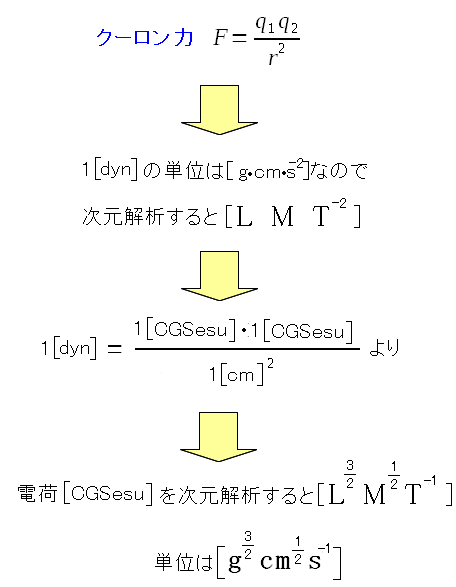
「dyn」とはCGS単位系での力の単位だ。同じ電荷を持った物同士を1cm話した際、斥力が1dynになる時電荷量を1CGSesuと決めたのだこの時、比例定数はK1=1にしたのだ。この時、決めたCGSと電荷の単位系の事をCGSesu単位系というのだ。


　CGS単位系にも種類があったとは

　知らなへんかった!!

　さて、電荷量の基本量が決まったので、単位と次元がわかる。

電荷の単位と次元(CGSesu単位系)

電荷のCGSesuの構成要素と指数がわかる。電荷の単位を決める事ができる。


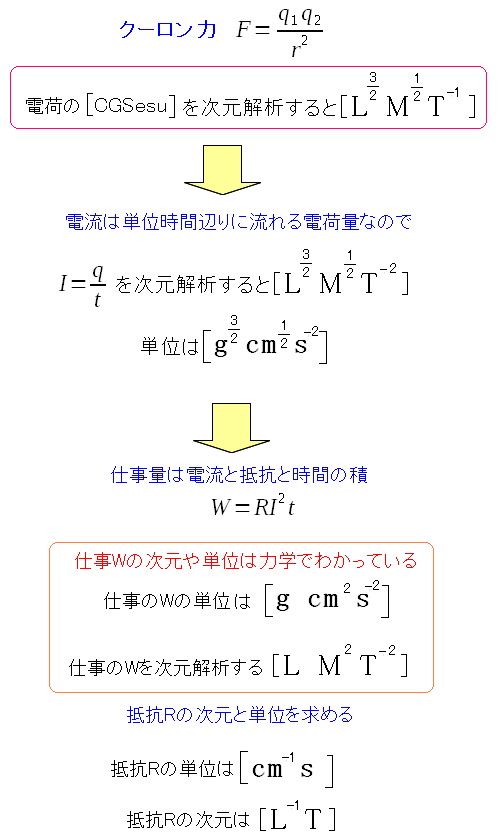
　電荷の単位と次元がわかると、電流や抵抗の単位や次元もわかる。

電流や抵抗などの単位や次元も決められる(CGSesu単位系)

既にわかっている電磁気の法則や、力学の単位を使うと電流や抵抗の単位や次元がわかる。


　改めて、クーロン力から決めていった単位系の事を

　静電単位系(CGSesu単位系)

　というのだ。


電磁単位系(CGSemu単位系)

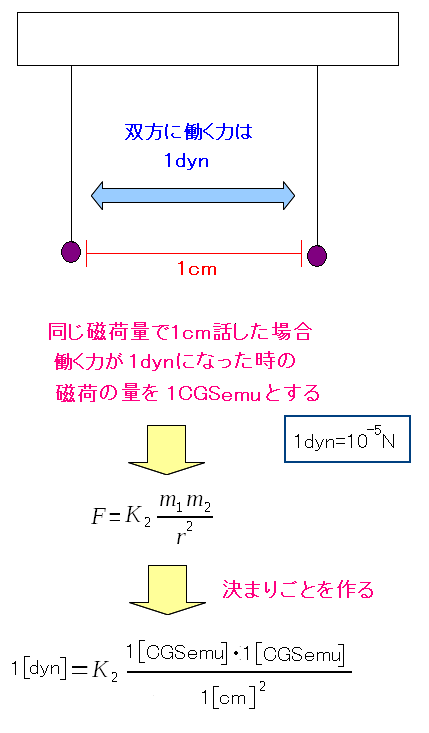
　静電単位系(CGSesu単位系)は電気の観点から生まれた単位系だった。
　今度は磁気の観点から生まれた単位系を見てみる。

　まずはCGSemu単位系で決められた磁荷の量の定義を見てみる。

CGSemu単位系で決められた磁荷の量の定義

電荷の量を決める[CGSesu]をクーロン力の関係式から定義したのと同様磁荷でも同じように決める。その際の磁荷量を「CGSemu」としたのだ。


　だが、磁荷なんて存在しない。
　だが、ビオサバールの法則の時と同様に

　電気素片を磁荷と考える

　ことはできるのだ。

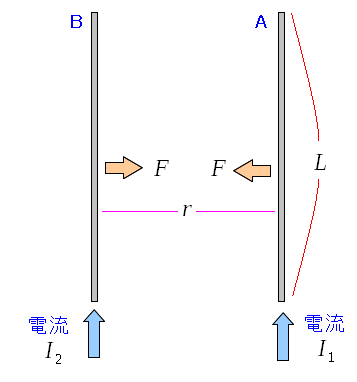
　長さLの2本の導線を平行にして電流を流した場合を考える

長さLの2本の導線を平行にして電流を流した場合を考える

長さLの2本の導線が平行に並んでいる。電流が同じ方向に流れていたら、引力が働く。アンペアの力で、アンペールが発見したものだ。


　平行する2本の導線間の引力だが、以下のように求めるという。

平行する2本の導線間の引力の求め方

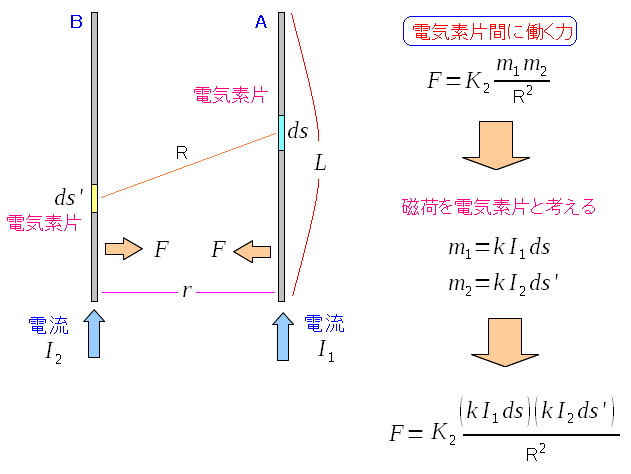
お互いの電気素片間に働く力を求める。クーロンの法則を磁荷に当てはめた感じの式になる。


　ところで片方の導線(導線B)の長さを無限と考える。
　導線Bが、導線Aの電気素片に働く力を求めるのだ。

導線Bが、導線Aの電気素片に働く力を求める

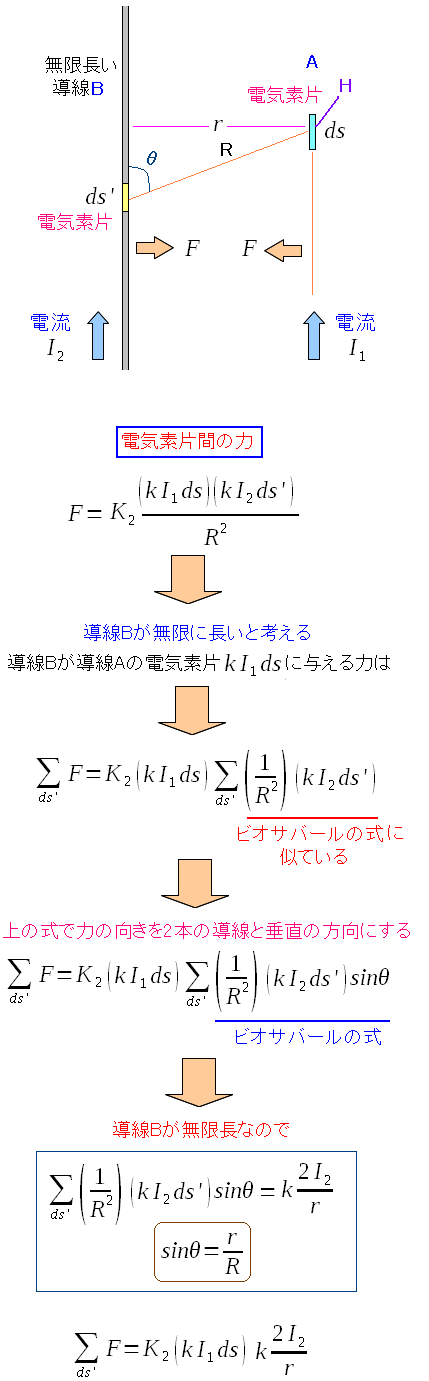
導線Bの電気素片が作る磁場が、導線Aの電気素片ではどれくらいなのかビオサバールの式と同じになる。そして導線Bの全体の電気素片は、無限に長い導線の電流が作る磁場の式と同じだ。導線Bが、導線Aの電気素片に働く力を求める事ができる。


　今度は導線A全体(長さL)に働く力を求める。

導線A全体(長さL)に働く力を求める

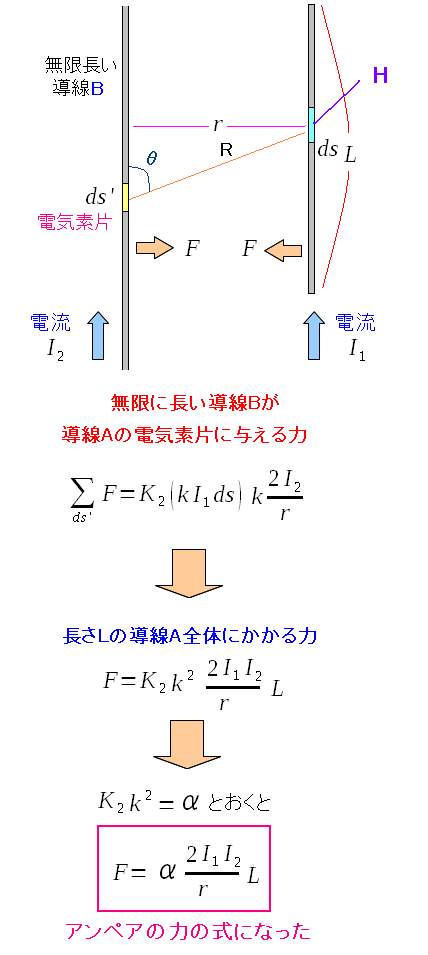
導線Bが無限に長くて、導線Aの長さがLなのでインチキ臭い所はある。だが、正しいアンペアの力の式になっているのだ。


　ここでようやく・・・

　CGSemu単位系での電流の定義ができる

　のだ。

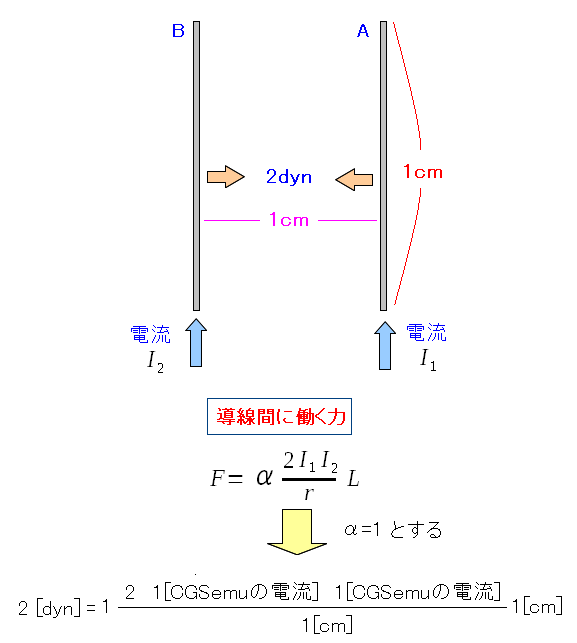
　2本の導線に電流を流した際に起こる引き合う力で、
電流の量を定義するのだ。

電流の量を定義 (CGSemu単位系)

電流は単位時間当たりに流れる電荷量なので電荷量が求められるのだ。でも、その方法は調べても、わからなかった・・・


　1800年代後半(19世紀後半)に、2つの単位系が登場した。
　だが、問題が起こった。

　CGSesu(静電)単位系とCGSemu(電磁)単位系との整合性

　の問題が起こったのだ。

電荷量の大きさは違う上、次元も異なる

単位電荷量の比率が3×10^10なので、これをcmと考えると光の速度になってしまう。そして次元も異なる。


　整合性があらへんやん!!

　という事態になったのだ。


有理化

　他にも問題があった。

　マックスウェルの方程式を綺麗に表現できへん

　だった。


　クーロン力、ガウスの法則などが発見された時は、
電荷の絶対量や電場の絶対量はわかっていない上
誘電率や透磁率なども決めていなかったため、比例定数が表現していた。

　当時のクーロンの法則とガウスの法則を見てみる。

19世紀後半のクーロンの法則とガウスの法則

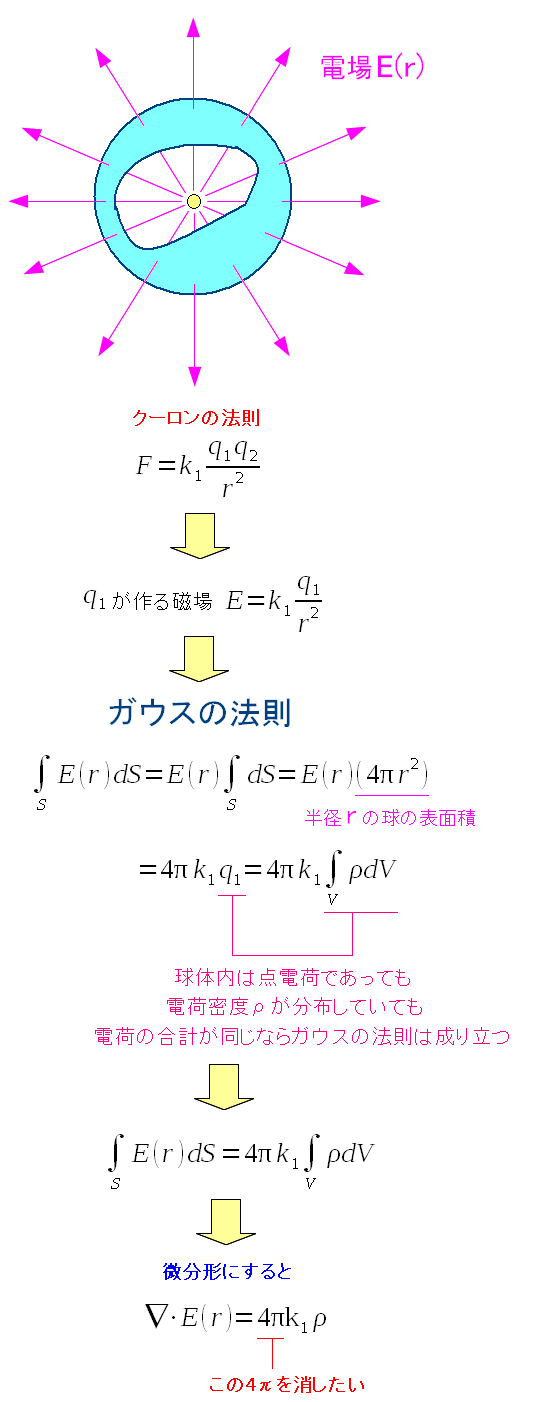当時は関係式は比例定数(値は不明)だった。
だが、クーロンの法則やガウスの法則は発見されていた。
そこでガウスの法則の微分形(マックスウェルの方程式の1つ)を求めてみる。

すると比例定数と共に「4π」の値がくっついてくる。
当時の物理学者(もしかしてマックゥウェルだけかも)は
4πを消したかったようだ。


　そこでマックスウェルの方程式から4πを消すため、比例定数を定義しなおす。

マックスウェルの方程式から4πを消したら、クーロンの法則に4πが出てきた

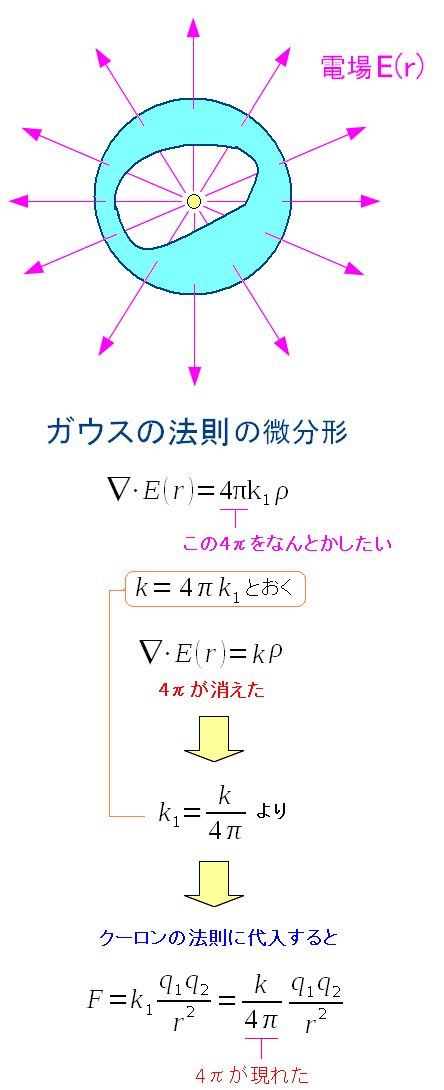クーロンの法則の部分に4πが出てくる理由だ。マックスウェルの方程式を綺麗に表現するための細工なのだ。


　電気の立場だけでなく、磁力の立場からも4πの存在を見てみる。

当時のビオサバールの法則

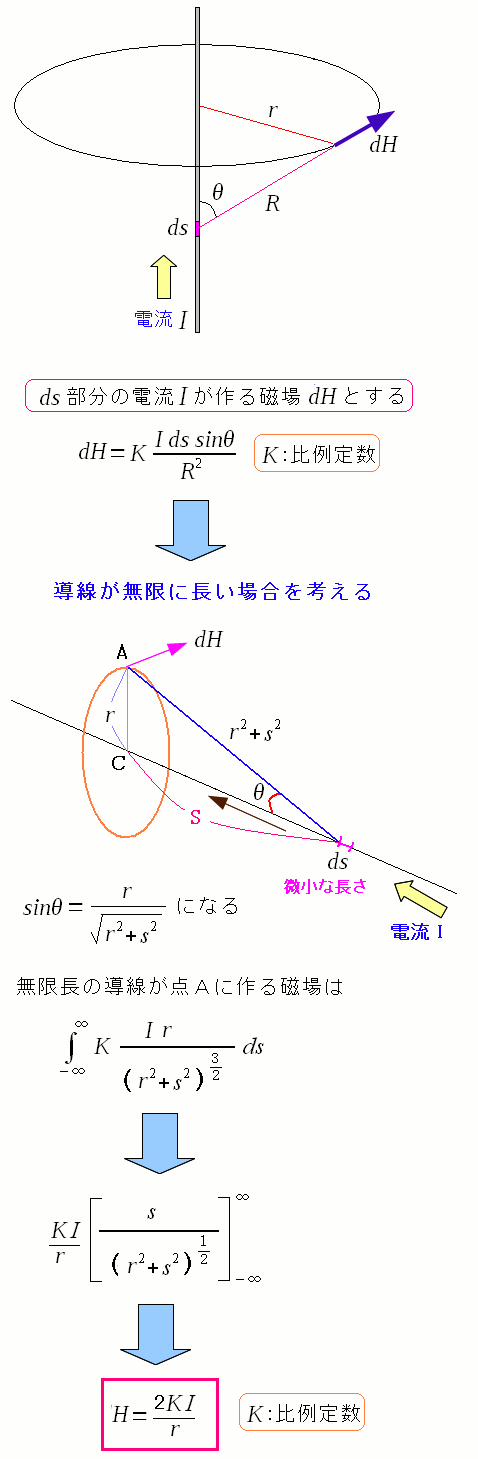まずは電気素片が作る磁場を求める式がビオサバールの法則だ。そして導線が無限に長い場合の、導線から垂直方向に、距離rの位置での磁場を求めるのだ。


　導線から垂直方向に、距離rの位置での磁場の強さがわかった。

　そしてアンペールの法則を考えてみる。

アンペールの法則

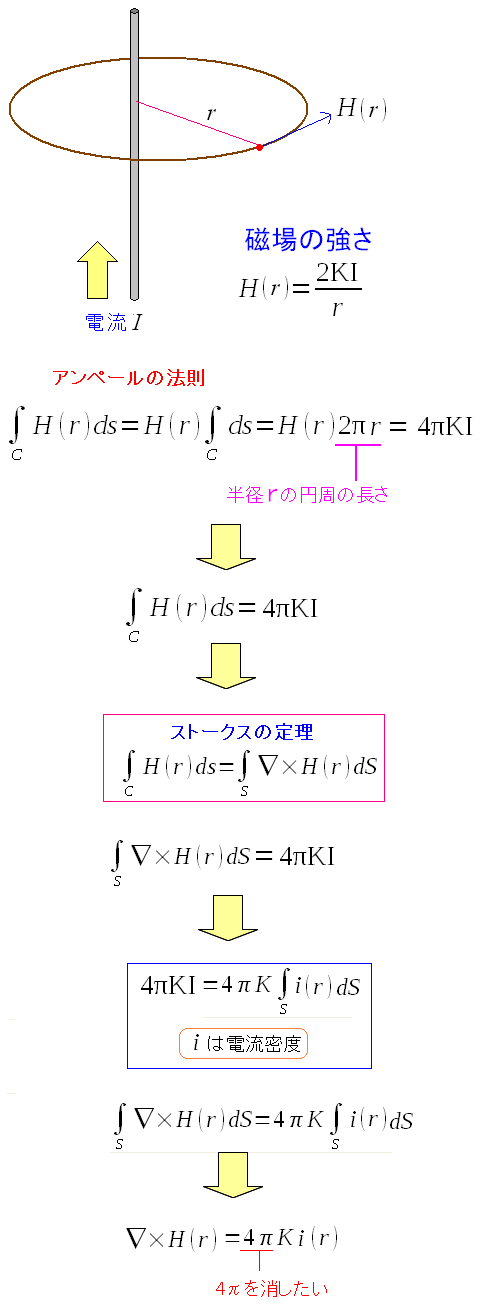求めた磁場をアンペールの法則に当てはめてみる。そこからアンペールの微分形を求めてみた。マックスウェルの方程式の1つになる。 (変位電流の項は、今回は無視してください) ここでも4πが出てくる。当時の物理学者は、4πを消したいようだった。


　マックスウェルの方程式から4πを消すため、比例定数を定義しなおす。

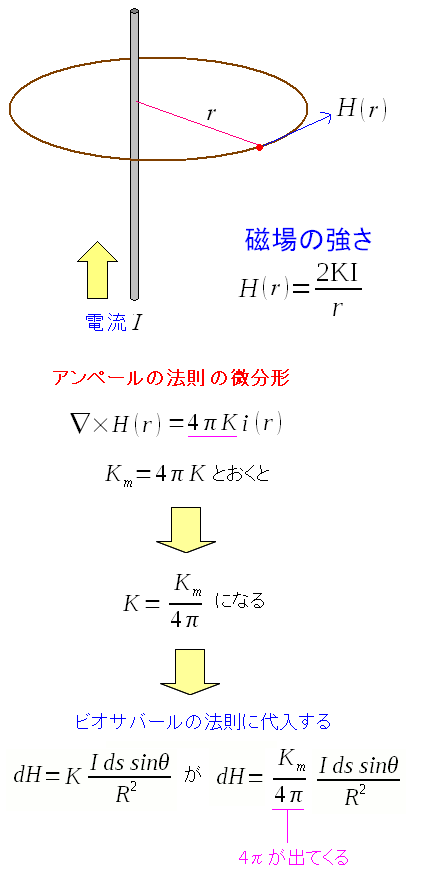
ビオサバールの法則に4πが現れる

マックゥウェルの方程式から4πを消したらビオサバールの法則に4πが現れた。マックゥウェルの方程式から4πを消すための小細工なのだ。


　マックスウェルの方程式から4πを消すため・・・

　クーロンの法則などの比例定数に4πが出現した

　のだった。


　4πを消すような作業の事を

　有理化

　というのだ。

　CGS単位系でも有理化を行なおうとしたようだが普及しなかったようだ。


　有理化だが、アンペールの法則も有理化してみる。

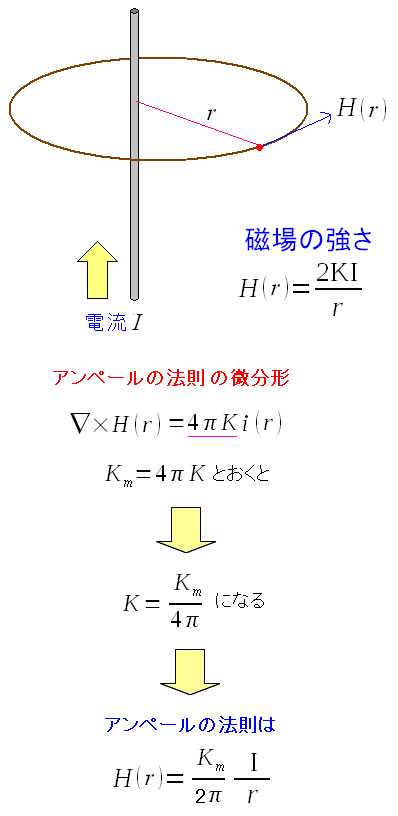
アンペールの法則に2πが現れる

アンペールの法則に2πが出現した。よく見ると2πrで、半径rの円周になっている。偶然だが「円周上の磁場を足し合わせた」という形が見えるようになっている。


　2本の平行に並んだ導線に電流を流した際にかかる力である
アンペアの力を求めてみる。

有理化したアンペアの力を求めてみる

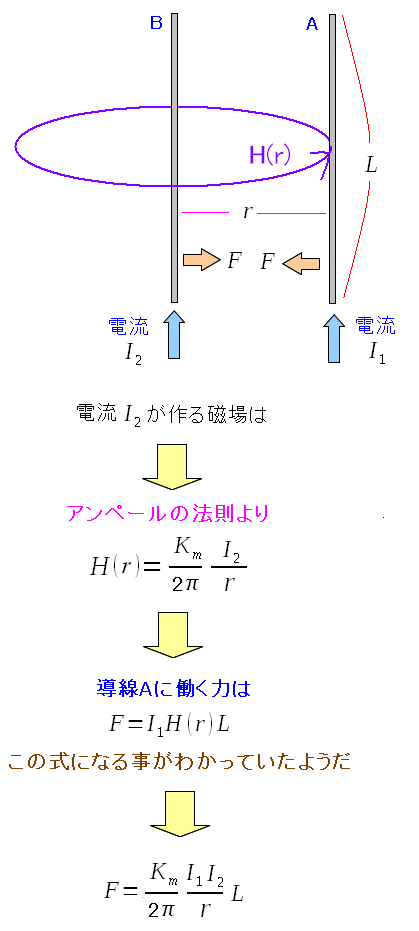2πが現れた形になっている。


　その後、紆余曲折しながらも国際会議を重ねていくうちに
MKSA有理単位系に落ち着いてくる。

　まずは真空中の透磁率の定義(MKSA有理単位系)だ。

　1948年の国際会議でMKSA有理単位系が決められた時

　だった。

　70年ぐらい前の話だ。意外と歴史は浅い。

透磁率の値

　まずは電流の基本量の1Aの定義が決められた。

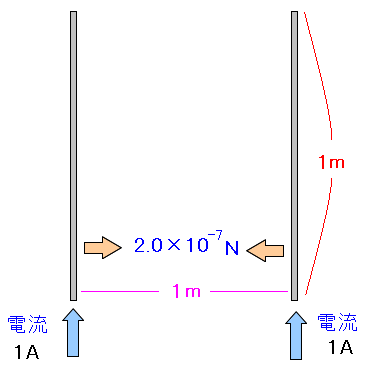
電流1Aの定義 (MKSA有理単位系)

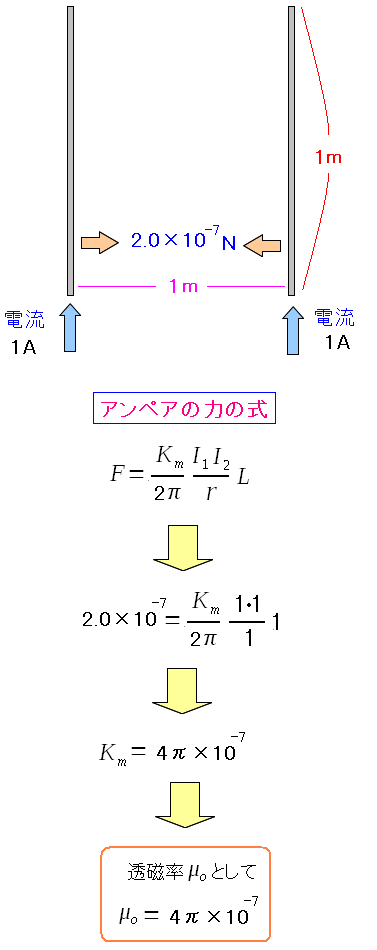
2本の平行した導線の間の距離を1mとして、導線の長さも1mとする。 2.0×10^(-7)Nの引力が働いた時の電流を1Aと定義した。


　そして同時に真空中の透磁率の定義も決まった、

真空中の透磁率の定義 (MKSA有理単位系)

透磁率の値が求まった。観測値でなく、定義値なのだ。



誘電率の値

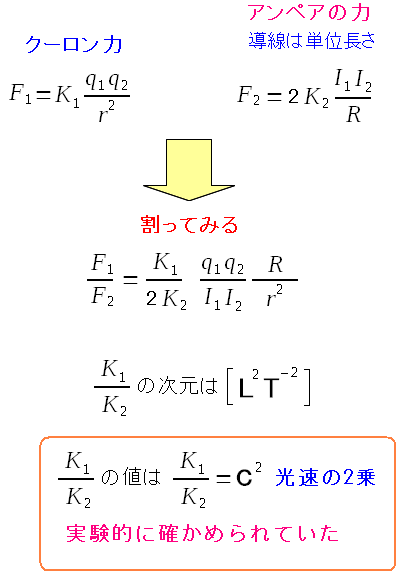
　次に誘電率の値だ。

　まずはクーロン力とアンペアの力の比較を行なう。

クーロン力とアンペアの力の比較 (CGS単位系)

比例定数の比は、速度の次元になっている上比例定数の比は、光速の2乗なのは、実験的に求められていた。どんな実験が行なわれて、光速の2乗を導いたのかは省略する。


　省略という言葉は便利

　なのだ。

　知っていても、知らなくても、わからなくても使えるのだ。
　知ったかぶりをしたい場合に有効な言葉だ。

　もちろん、私の場合は・・・

　調べてみたが、流れが理解できへんかった

　なのだ。
　格好つける気はないし、格好つけてもメッキは剥がれるので
正直に書くのだ。

　そして誘電率が出てくる。

真空中の誘電率 (MKSA有理単位系)

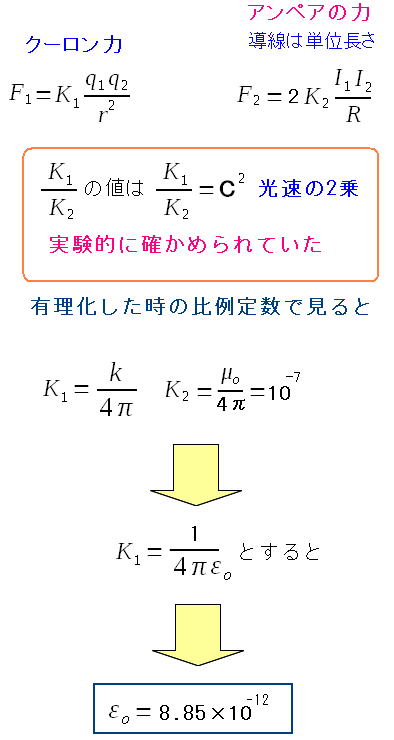光速という測定値が絡むため、真空中の透磁率のように綺麗に決まらない。


　中途半端な電磁気学の歴史と単位系の話になったのだが
調べてみたお陰で、4πがつく理由と、透磁率、誘電率の由来を
垣間見る事ができた。


電磁気学入門の目次

電磁気学入門:目次
スカラーとベクトル	簡単なスカラーとベクトルの話です。ベクトルは方向と大きさを持つ量。方向という量持っているだけに注意が必要です。
静電気の発見からクーロンの法則	今でこそ当たり前の静電気や導体、絶縁体、電荷などどういう経緯で発見し、クーロンの法則まで至ったのかの話です。
クーロン力、電場、近接作用	4つの力のうち、クーロン力の位置づけ電荷が作り出す作用の電場。近接作用の話です。
微分、全微分、方向微分	簡単な微分、全微分、方向微分の話です。ここをしっかり押さえないと、電磁気の数式の意味がわからなくなります。
ベクトル解析	電磁気に必要なベクトル解析の話です。勾配(grad)、2次元のグリーン定理ストークスの定理の話です。
電位ポテンシャル	電位ポテンシャルです。勾配と電場の関係を使って説明しています。
電気双極子	電気双極子の話です。物質中で起こる分極を理解するのに必要です。
ガウスの法則	ガウスの法則の積分形、微分形の話です。
ポアソンの方程式、ラプラス方程式	ポアソンの方程式、ラプラス方程式の話です。単に電荷分布から電位を求めるだけの話にとどまらない奥が深い分野です。ポテンシャル論、デルタ関数グリーン関数、固有値問題について触れています。
静電場と渦なしの法則	静電場で、電荷を1周させた時の仕事はゼロ微分形と微分形の渦なしの法則の話です。
ビオサバールの法則	電気と磁場の関係の発見の話からビオ・サバールの法則が導かれるまでの話です。
磁気双極子	磁気双極子の話で、回転電流になります。物質中の磁場の話にも関連します。
アンペールの法則	アンペールの法則の話です。積分形・微分形だけでなく、閉回路に流れる電流が作る磁気双極子の話なども書いています。
ローレンツ力	磁場中を移動する電荷にかかる力(ローレンツ力)の話です。ローレンツ力は相対性理論が絡んでいる事も紹介しています。
ファラデーの誘導起電力の法則	ファラデーの誘導起電力の話です。
うず電流を使った簡単な物理実験	電力計に使われるアラゴの円盤。そしてIH調理器で熱するために発生させる、うず電流はレンツの法則から電流が発生する原理を応用した物だ。アラゴの円盤の実験と、IH調理器を使った実験です。気分転換で読んでください。
ベクトルポテンシャル	わかりにくいベクトルポテンシャルの話です。電位は電荷が作る電気のポテンシャルだがベクトルポテンシャルは電流が作る磁場のポテンシャルの話です。
オームの法則の微分形	微小領域でのオームの法則の話です。
マックスウェルの方程式	4つのマックスウェルの方程式を書いています。電場と磁場の変化を図にする事で rotの回転の意味も理解できます。
ゲージ変換	ゲージ(gauge)は物差しの意味です。マックスウェルの方程式をE（電場）とB(磁場)の関係式から φ(電位ポテンシャル)とA(ベクトルポテンシャル)の関係式に書き換える際、ゲージ変換が使われます。ゲージ変換の役目を書きました。
電磁波	マックスウェルの方程式から電波が伝わる様子を視覚的に見てみる話です。
回転のrotはベクトルの微分	ベクトル解析や渦なしの法則で出てくるrotはベクトルの微分という話です。
電磁気学の単位系	電磁気学の単位系の話です。物理量の単位系の指数を見る次元解析電磁気学の歴史と単位系の変遷について触れました。
電気泥棒:電気と法律の話	電気は物体なのか、無形物なのか。明治時代に、電気を無断で使った場合、物か、そうでないかで窃盗罪になるかどうかが裁判で問われました。ちょっとした科学と法律の話です。気分転換で読んでください。
数ベクトルと基底ベクトル	ベクトルの話です。矢印だけがベクトルでない事。数ベクトルと基底ベクトルの違いの話です。多様体、反変・共変ベクトルを理解するのに必要です
多様体	空間を一般化した話です。 ▽(ナブラ)の正体に迫まります
外積代数	外積、テンソルについて書いています。極性ベクトル、軸性ベクトル外積は行列で、ベクトルは見せかけの姿だった話です。
ベクトルの双対関係	反変ベクトル、共変ベクトル、双対関係ベクトル解析、外積代数の話外積、テンソルについて書いています。
ローレンツ力と相対性理論	磁場は電場の相対論的効果だった話です。ローレンツ力を使って、導線が作る磁場を使って説明です。
微分形式	多様体の話の続きです。座標に依存しない形での関数やベクトルの微分の話です。ガウスの法則、アンペールの法則、マックスウェルの方程式が鮮やかな形で表現できます。 ∇(ナブラ)の正体もわかります。
物理と対称性	マックスウェルの方程式をよく見ると対称性があります。物理の方程式と対称性を数学的な観点でみると意外なつながりがあるという話です。
マックスウェルの応力	電気力線を弾性体(ゴム)とみなして、力の伝わり方などを説明した考え方です。
電場エネルギー	電場が持つエネルギーの式を導いた話です。
磁場エネルギー	磁場が持つエネルギーの式です。手抜きの説明と、直流RL回路を使った説明を書きました。
ポインティングベクトル	電磁エネルギーの流れ「ポインティングベクトル」の話です。電磁波でもエネルギー保存則が成り立つ話からポインティングベクトルを導いています。
電気エネルギーは導線の外を伝わる	導線の外を電気エネルギーが流れる話です。私が誤解した事、その誤解を解いていく過程を紹介しながら「目からウロコ」にたどり着いた話です。
物質中の電場	物質中の電場の話です。分極の話をしながら、物質中の電場の話をします
物質中の磁場	磁性の話をしながら、物質中の磁場の話をします
物質中のマックスウェルの方程式	物質中でもマックスウェルの方程式が成り立つ話です。
導体に侵入する電磁波	導体に侵入する電磁波が減衰していく話です。表皮効果と同じ「表皮の厚さ」が出てきます
表皮効果	目的の表皮効果の話です。マックスウェルの方程式を解きながら交流電流の周波数を上げると、表面にしか電流が流れなくなる話です。

電磁気学の目次:「電磁気学入門」に戻る

前章:「無線LANの基礎無線LAN入門と導入事例」を読む
システム奮闘記の目次:システム奮闘記に戻る