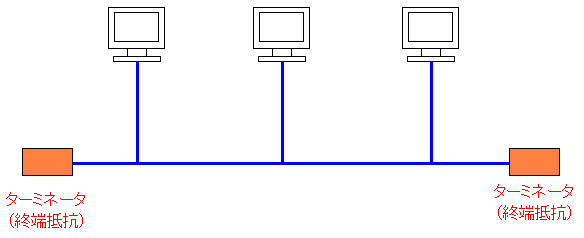
ケーブルの両端にはターミネータ(終端抵抗)がある。
信号の反射による信号の乱れを防ぐための物だ。
システム奮闘記:その106
(2016年11月14日に掲載)
はじめに LANの事を調べている時、昔はLANケーブルは同軸ケーブルだった事を知る。
| 10Base5時代のLAN |
|---|
 |
|
一本の線でつながっていた。 ケーブルの両端にはターミネータ(終端抵抗)がある。 信号の反射による信号の乱れを防ぐための物だ。 |
それ以外にも身近な
テレビのアンテナ線
も同軸ケーブルなのだ。
| テレビのアンテナ線 |
|---|
 |
| 身近な所にも同軸ケーブルがある。 |
そして差込口だ。
| テレビのアンテナ線の差込口 |
|---|
 |
| 自宅のアンテナ線の差込口だ。 |
ところで同軸ケーブルは単線だ。信号線が1本だからだ。 だが、後になって、当たり前の事に気づく。 電気って行きと帰りがあるはずやん!! 単線だと 帰り線はどこにあるねん? だった。
| 同軸ケーブルの行きと帰りの線 |
|---|
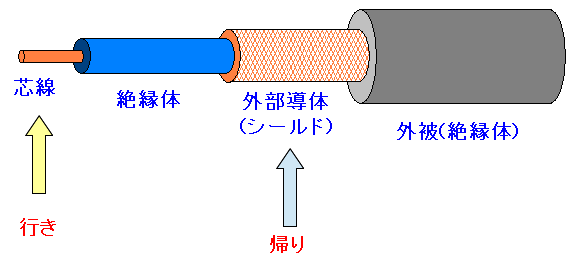 |
| 内部導線が行きで、外のシールドが帰り線になっている。 |
こんな事、知らへんかった!!
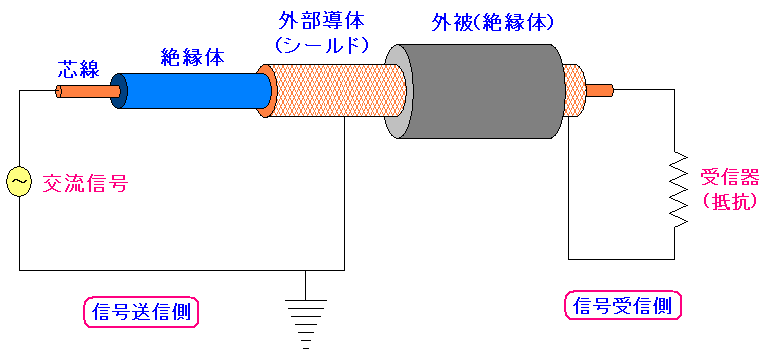
これを入力部と出力部の間に同軸ケーブルを入れた図にしてみた。
| 入力部と出力部の間に同軸ケーブルを入れた図 |
|---|
 |
|
交流信号の行きは、内部導線を伝わり 帰りは、外側の導線(シールド)を伝わる。 |
でも、これだけでは終わらなかった。 調べていくと、色々、出てきたのだ。
コンデンサーとコイルの回路
同軸ケーブルについて調べていくと同軸ケーブルは コイルとコンデンサーの回路やん!! なのだ。 同軸ケーブル内ではコイルとコンデンサーが同居している。 高周波回路のお話(PDF) 同軸ケーブルの基礎と選び方(PDF)
| 同軸ケーブルの等価回路 |
|---|
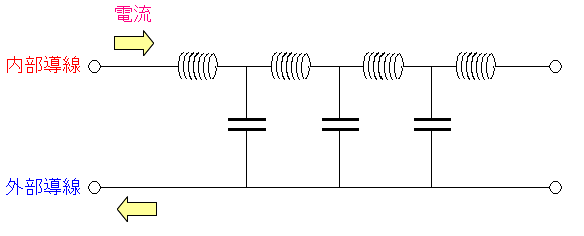 |
| 同軸ケーブルはコイルとコンデンサーを持つ回路になっている。 |
なんでやねん? そこで同軸ケーブルのコンデンサーの性質を持つ理由を見てみた。コンデンサーと電気容量
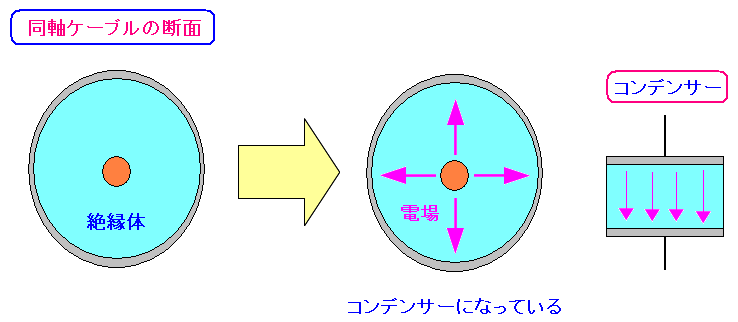
同軸ケーブルがコンデンサーの性質を持っている。
| 同軸ケーブルのコンデンサーの性質 |
|---|
 |
|
内部導体と外部導体が、コンデンサーの極板の役割をする。 内部導体と外部導体のの間に詰めた絶縁体(誘導体)が コンデンサーの極板間に詰めた誘導体と同じ役目をする。 |
ところで同軸ケーブルはコンデンサーの役目を持つ事がわかったので
電気容量を求めてみたい。
導き方を調べると以下のサイトを発見した。
Maxwell方程式と伝送線路 その4 同軸線の解析的な特性計算 - パワエレ・EMC日記
導波路・伝送線路の解析(電気通信大学:PDF)
こんな所で
ラプラス方程式が使えるんだ!!
だった。
| ラプラス方程式 |
|---|
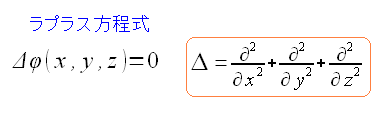 |
|
ラプラス方程式は、ポテンシャルの源泉(電荷)でない場所ではゼロになる 微分方程式なのだ。 詳しくは「システム奮闘記:その105」(電磁気学入門)の中にあります ポアソン方程式、ラプラス方程式をご覧ください |
求めたいのは同軸ケーブルの絶縁体内部の電場だ。 その前段階として、同軸ケーブルの絶縁体内部での電位を知る必要がある。
| 電場を知るために、電位を知る必要がある |
|---|
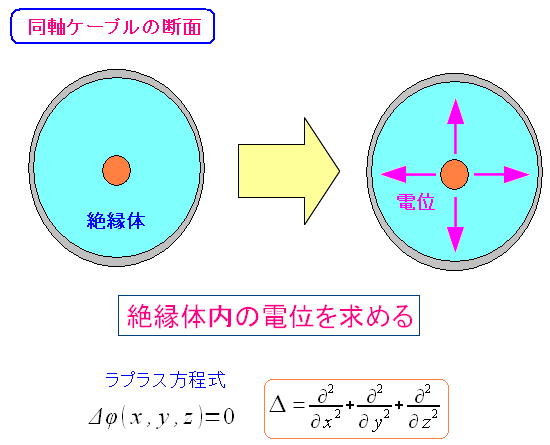 |
| この時、ラプラスの方程式を使う。 |
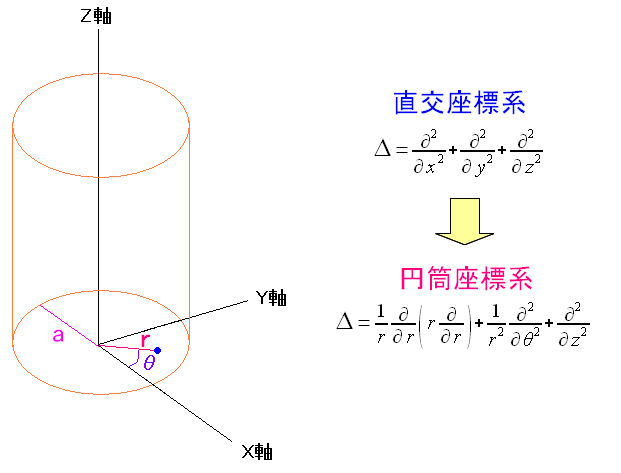
ところで同軸ケーブルの場合、直交座標系を使うよりも 円筒座標系を使った方が便利だ。
| 同軸ケーブルの場合、円筒座標系を使った方が便利 |
|---|
 |
|
同軸ケーブルの場合、円筒座標系を使った方が便利なのだ。 ラプラシアンを直交座標系から円筒座標系への変換した際の導き方は 「システム奮闘記:その105」(電磁気学入門)の中にあります 表皮効果をご覧ください |
ところで電場は、座標の中心にある導線から放射状に伸びている。 それを上手に使うと、電場は中心からの距離の関数になる。
| 電場は中心からの距離の関数になる |
|---|
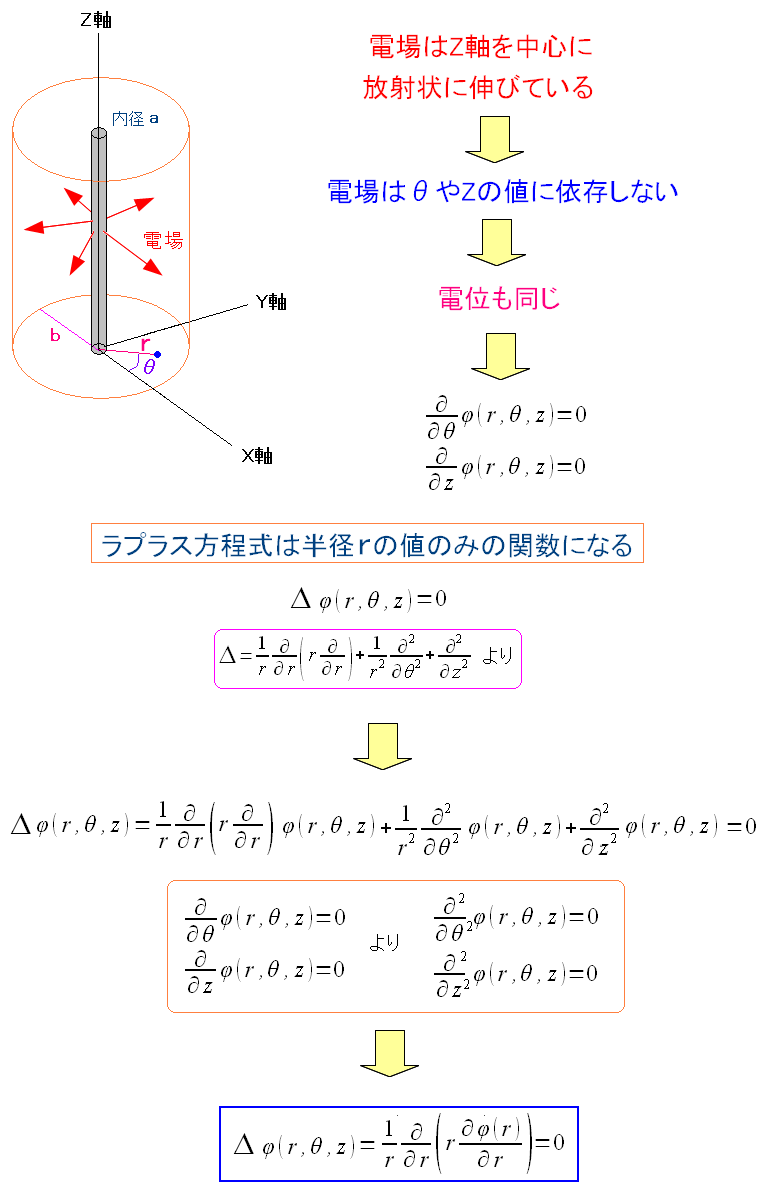 |
| 電場は中心からの距離の関数になるので、計算が楽になる。 |
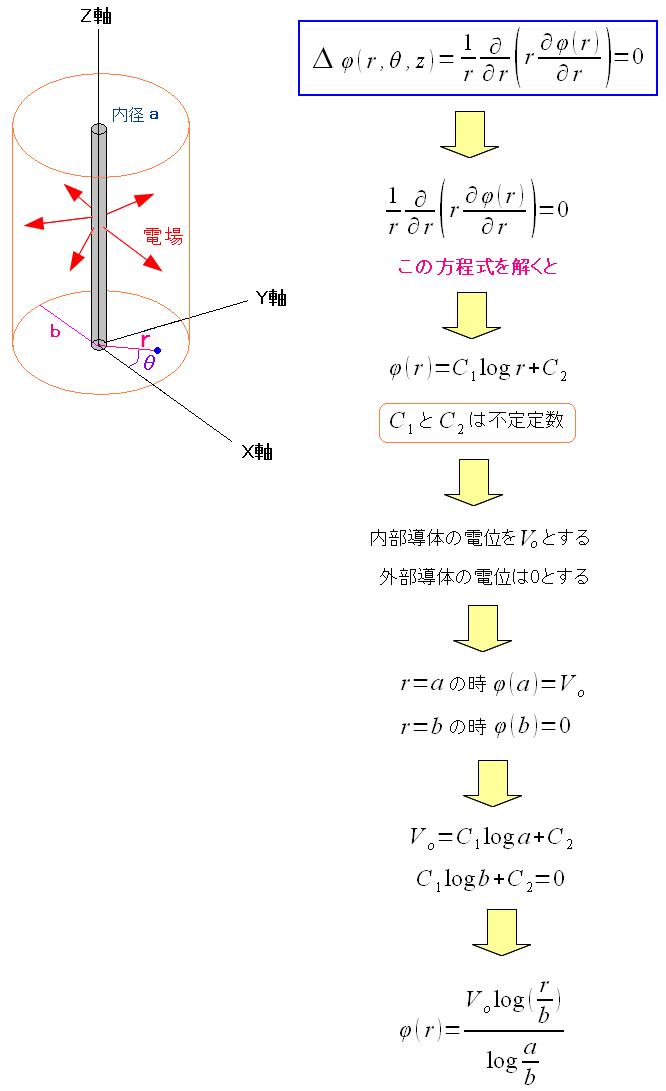
ラプラス方程式を解いてみる
| ラプラス方程式を解いてみる |
|---|
 |
|
内部導線の電位をVoとし、外側の網目(外部導線)の電位をゼロとすると 不定定数が消去される。 |
電場は電位の勾配にマイナスをつけた物なので
| 同軸ケーブル内の電場が求まる |
|---|
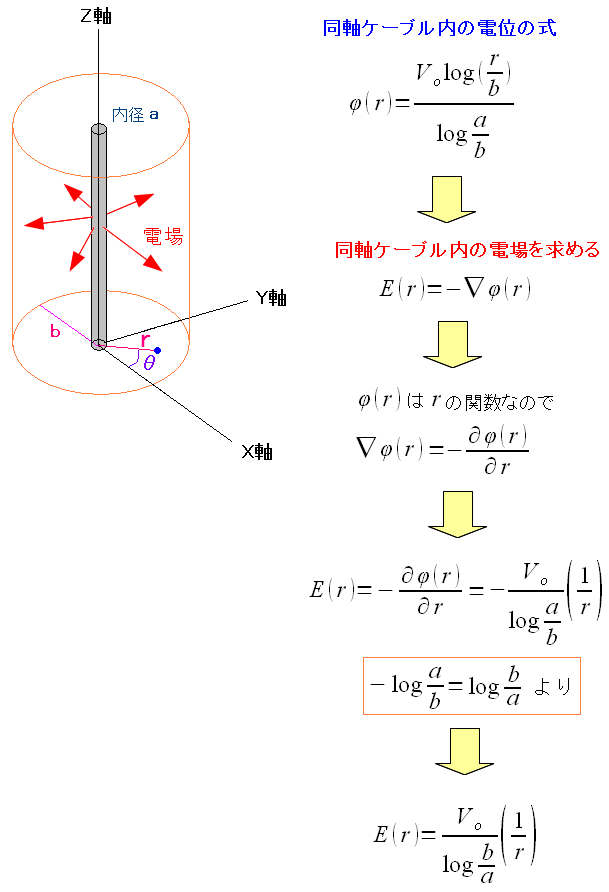 |
| 同軸ケーブル内の絶縁体内での電場が求まった。 |
電場が求まったので、コンデンサーの値である電気容量を求めてみる。
| 同軸ケーブルの単位長さ辺りの電気容量 |
|---|
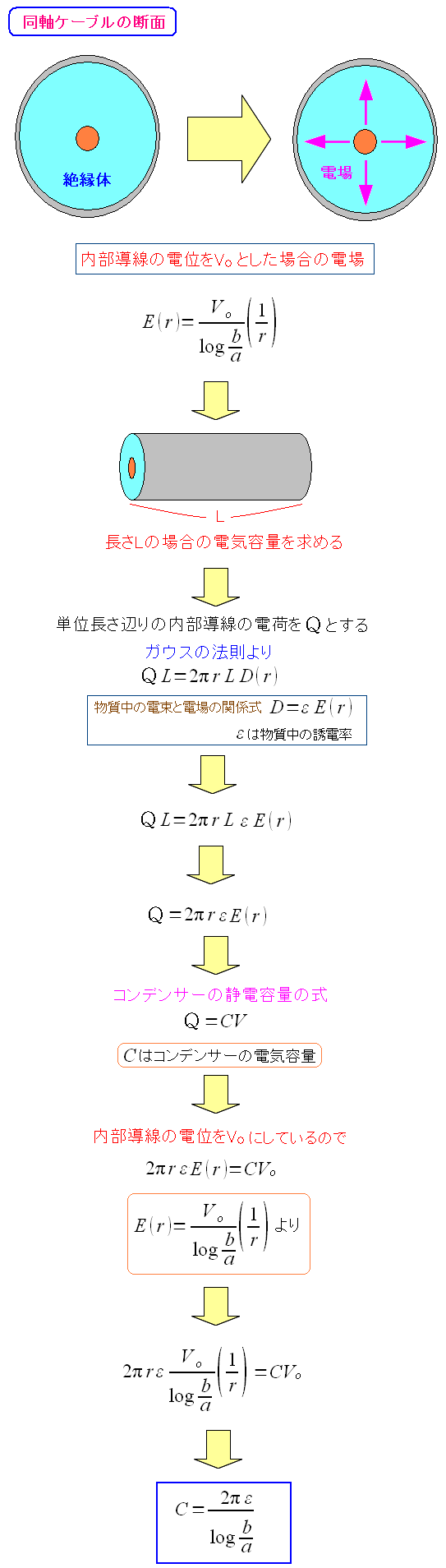 |
| 内部導線の電位に依存しない形で求まった。 |
コイルとインダクタンス
同軸ケーブルは、コンデンサー以外にもコイルの役目もあるのだが・・・ コイルの役目をする理由がわからへん!! そこで調べてみたら、以下のサイトを発見。 電磁気学II2007年度第12回(琉球大学:前野さんの資料) 納得できた。つまりこういう事なのだ。
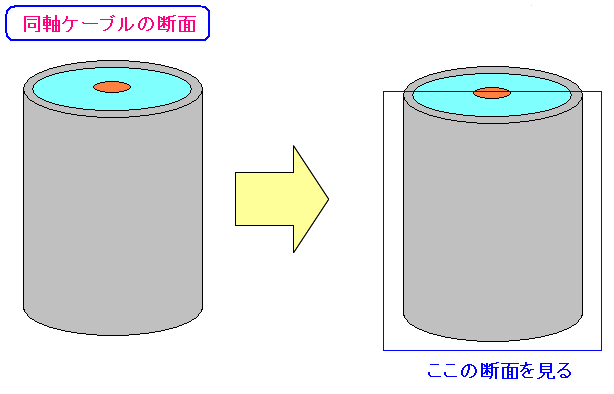
| 同軸ケーブルの断面を考える |
|---|
 |
|
同軸ケーブルがコイルの性質があるのを知る手がかりとして 同軸ケーブルの断面を考える必要がある。 |
断面の様子を見る。
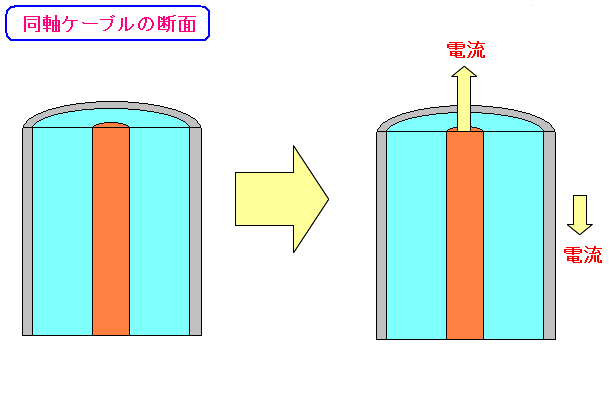
| 同軸ケーブルの断面 |
|---|
 |
|
中心に内部導線があり、外側に外部導線があり それぞれが反対方向に電流が流れている。 |
そこで電流が作る磁場を見てみる。 こういう時はアンペールの法則を使う。
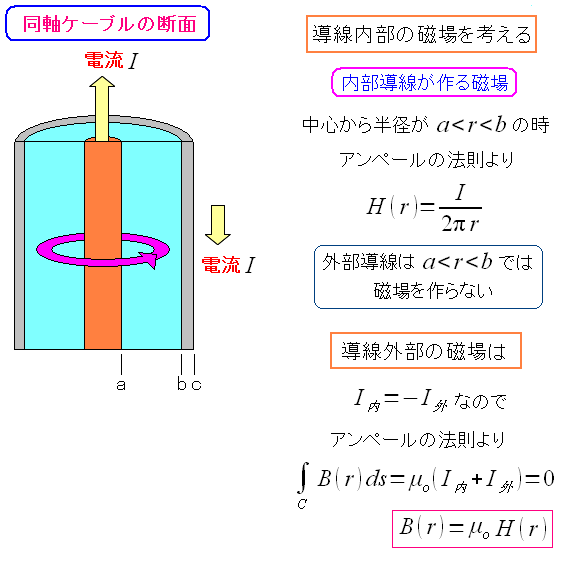
| 電流が作る磁場 |
|---|
 |
|
内部導線が作る磁場は中心から距離に反比例している。 同軸ケーブルの外側では磁場はゼロになる。 内部導線が作る磁場と、外部導線が作る磁場で相殺されているのだ。 |
コイルの話をする前に、磁束と電流の関係の話をする。
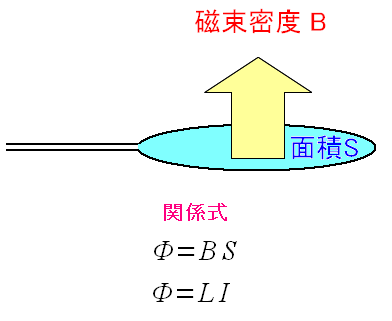
| 磁束と電流の関係 |
|---|
 |
|
磁束は、磁束密度と面積の積になる。 閉回路において、磁束と電流は比例関係になる。 この時の比例定数Lの事を、自己インダクタンスという。 もしくは、単にインダクタンスと呼ぶ。 インダクタンス(東京工業大学:PDF) |
同軸ケーブルは、以下の閉回路としてみることができる。
| 同軸ケーブルは閉回路 |
|---|
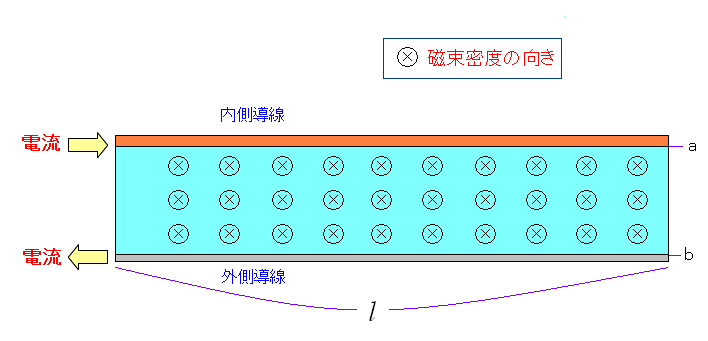 |
| 同軸ケーブルは、上図のような閉回路としてみることができる。 |
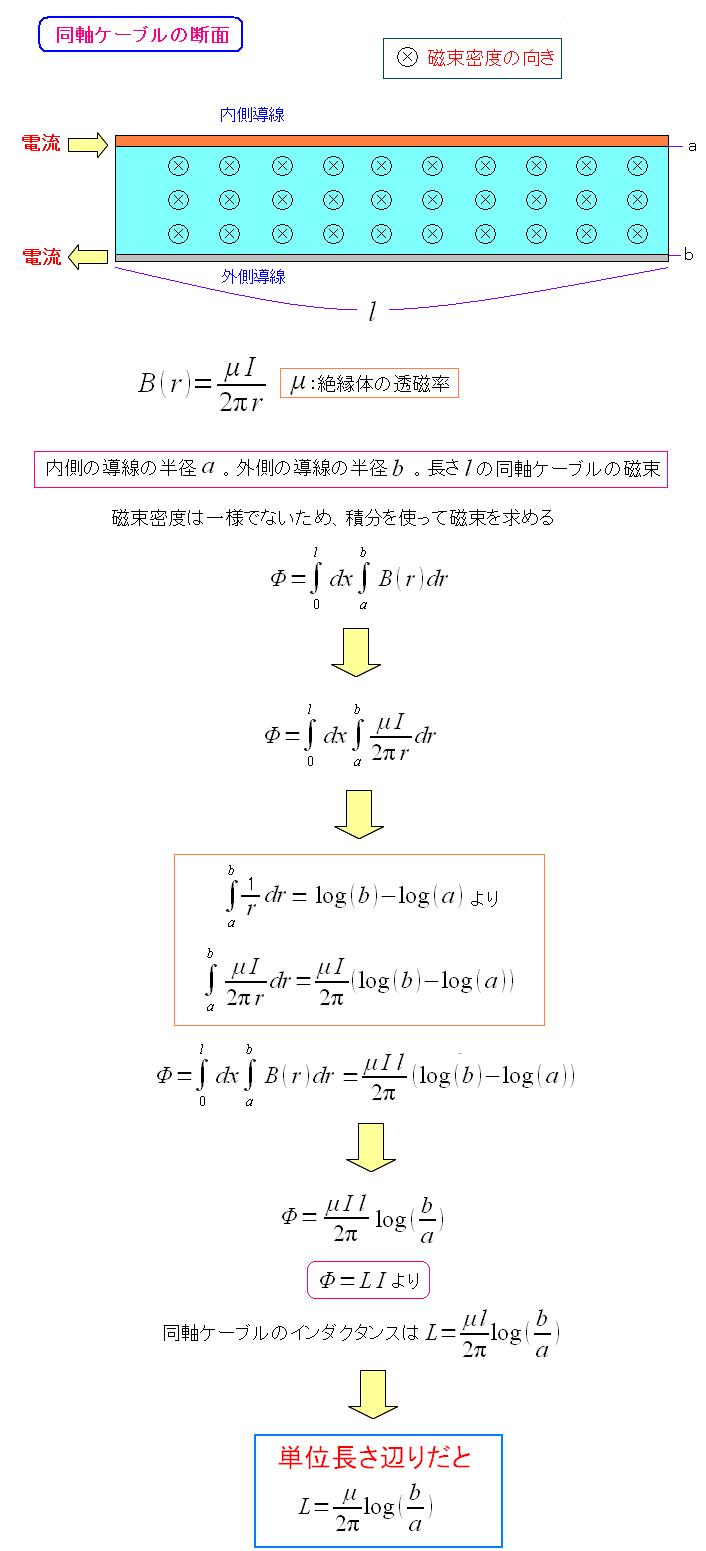
そこで磁束と電流の関係式から、同軸ケーブルの自己インダクタンスを求めてみる。
| 同軸ケーブルの自己インダクタンスを求めてみる |
|---|
 |
|
閉回路の磁束密度は、一様ではないため、積分を使って、磁束を求める。 そして単位長さ辺りの同軸ケーブルの自己インダクタンスを求まった。 |
分布定数回路
いきなり最初から 分布定数回路って何やねん なのだ。 そこで調べてみた。 分布定数回路〜何が分布しているのか(elspear社) 分布定数回路(東京工業大学・講義資料) 技術の渚 ここでの定数とは、コンデンサーやコイルといった 回路素子 なのだ。 さて、さきほど同軸ケーブルの単位長さ辺りのインダクタンスと電気容量が求まった。 単位長さ辺り というのが重要になってくる。 同軸ケーブルの場合、一様にコイルとコンデンサーを持っているからだ。
| 同軸ケーブルの等価回路 |
|---|
 |
|
同軸ケーブルはコイルとコンデンサーを持つ回路になっている。 図ではコイルやコンデンサーが間隔をおいているようになっているが 実際の所は、一様に分布している。絵で書くのが難しいので飛びとびになっているのだ。 |
そのため単位長さ辺りのインダクタンスや電気容量の値が必要になってくるのだ。
特性インピーダンス
同軸ケーブルにはコイルとコンデンサーの性質がある。 それによって、何が問題なのかを見てみる。 特性インピーダンスの問題なのだが・・・ 特性インピーダンスとは何やねん? なのだ。 同軸ケーブルだと50Ωとか75Ωなどがある。
| 自宅のテレビのアンテナ線は75Ωだった |
|---|
 |
|
自宅のテレビのアンテナ線の所に75Ωの表記があった。 この値は、自宅のテレビのアンテナ線に使われている 同軸ケーブルの特性インピーダンスなのだ。 |
単位は「Ω」なのだが、どうも抵抗値とは違うようだ。 そこで調べていくと特性インピーダンスとは・・・ 伝播する電圧と電流の比 なのだ。 単なる比率であって、よく言われる インピーダンス(抵抗) とは違うのだ。 ところで同軸ケーブルでの特性インピーダンスとは図にすると以下のようになる。
| 特定インピーダンスとは |
|---|
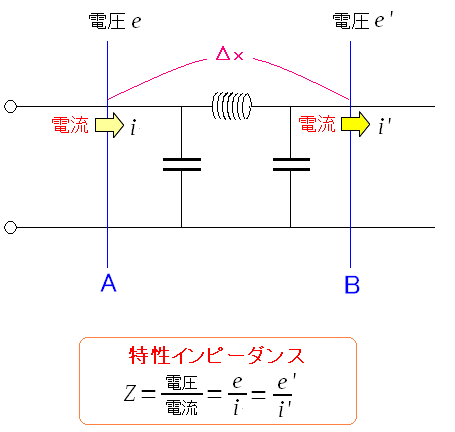 |
| どこの部分を見ても、電圧と電流の比が同じになるのだ。 |
特性インピーダンスを求めるために、同軸ケーブル内の 電圧と電流を求めてみる事になる。 そこで以下の資料を参考にした。 分布定数回路(東京工業大学) エレクトロニクスデザイン(慶応大学) 特性インピーダンス(東京大学) 「参考にする」だと格好良いのだが、実態は 資料の丸写し なのだ。 計算を簡単にするため 同軸ケーブル内の導線の抵抗をゼロと考える と資料に書いているので、そのまま丸写し。 同軸ケーブル内でも場所によって電圧と電流が異なる。
| A地点とB地点での電圧と電流の関係式 |
|---|
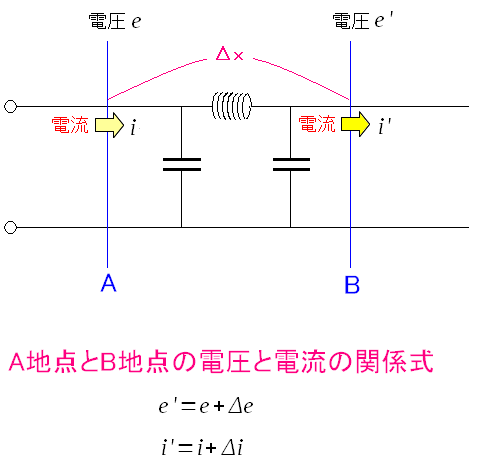 |
| 2つの地点での電圧と電流の関係式を求めてみる。 |
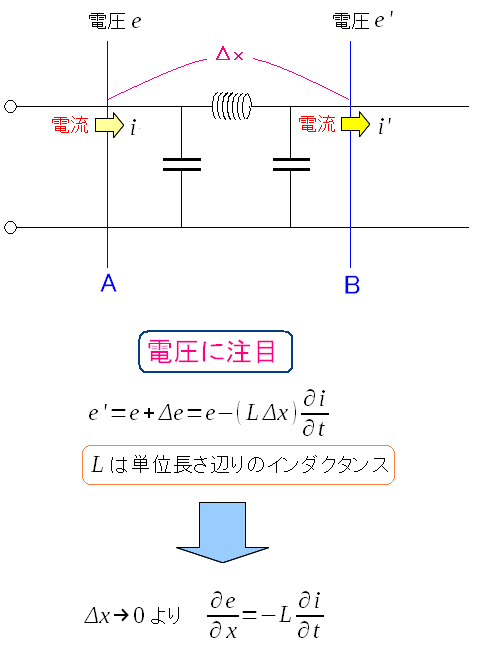
まずは電圧に注目する。
| 同軸ケーブル内での電圧に注目する |
|---|
 |
|
位置がΔxだけ移動すると、その分、コイルのインダクタンスが働き 電圧が変化する。 電圧と電流の関係式が出てくる。 |
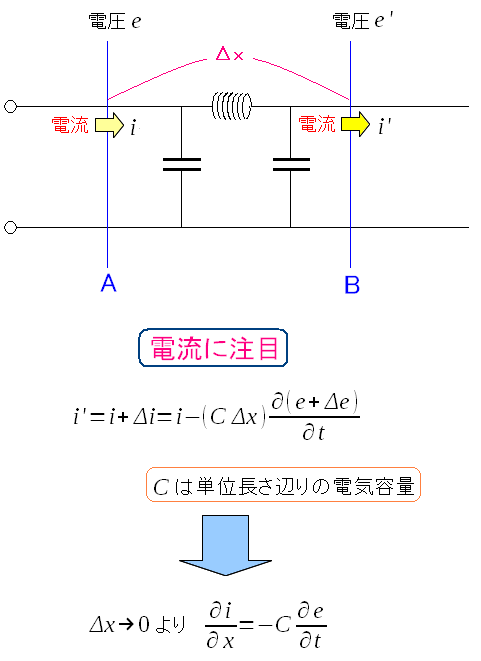
次に電流に注目する。
| 同軸ケーブル内での電流に注目する |
|---|
 |
|
Δxだけ移動した分、電流がコンデンサーを流れるため 電流が変化する。 電圧と電流の関係式が出てくる。 |
2つの関係式が出てきた。 電圧と電流のそれぞれの関係式に分離してみる。
| 電圧と電流のそれぞれの関係式に分離してみる |
|---|
 |
|
それぞれ電圧と電流を分離させる事に成功。 電圧の関係式と、電流の関係式が求まった。 上のような式を波動方程式というのだ。 |
ところで・・・
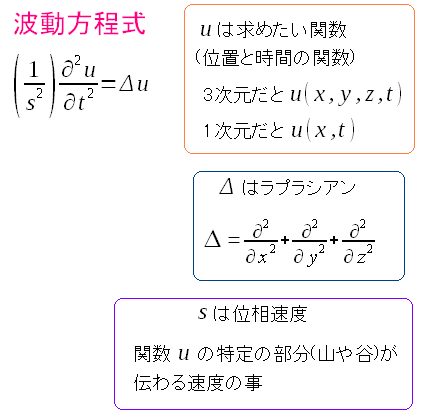
波動方程式って何やねん??
| 波動方程式 |
|---|
 |
|
波動方程式とは上図のような微分方程式の事を言う。 弦の振動をはじめ、様々な所で出てくるという。 |
とはいえ・・・
波動方程式を見たのは初めて!!
なのだ。
もちろん、自信はない。単に学生時代に講義で出てきたが
寝ていた、もしくは覚えていないだけかもしれない。
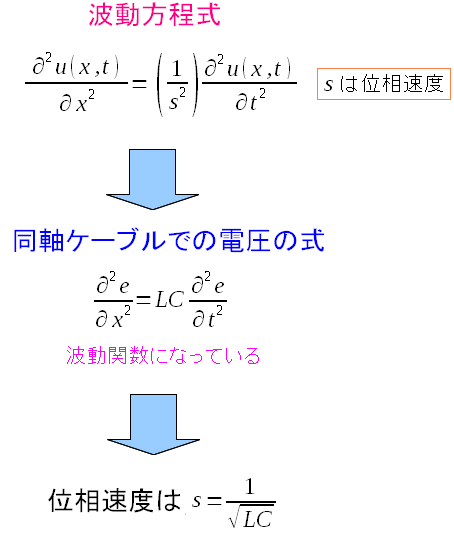
| 同軸ケーブル内の電圧に関する波動関数を見てみる |
|---|
 |
|
電圧の伝わる速度(位相速度)がわかる。 同軸ケーブルの長さとは関係ないのだ。 |
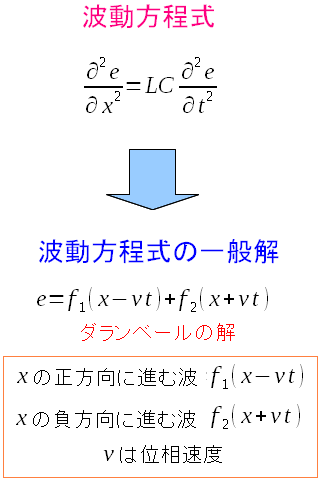
波動方程式の解として
ダランベールの解
がある。
| ダランベールの解を使って、電圧の式を求める |
|---|
 |
|
(x - vt)を変数とした関数と、(x + vt )を変数とした関数の 合成関数が、波動方程式の解になるのだ。 (x - vt)を変数とした関数は、x方向の正の向きの波となり (x + vt)を変数とした関数は、x方向の負の向きの波になるのだ ダランベールの解を用いて、電圧の式が求まるのだ。 |
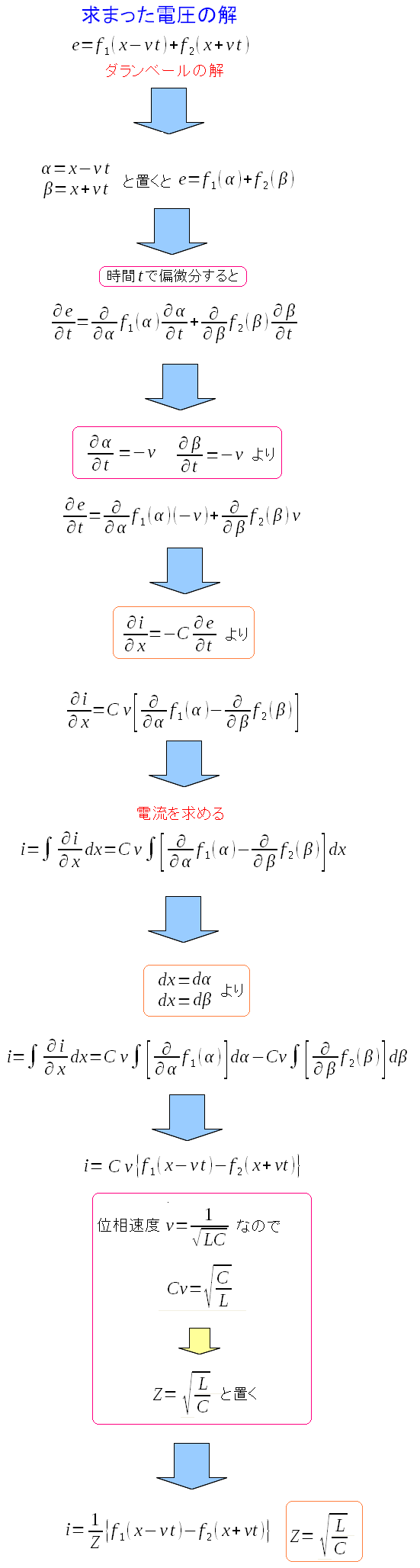
ダランベールの解で、電圧の式が求められる。 そこから電流の式を求めてみる。
| 電流の式を求めてみる |
|---|
 |
|
ちょっと計算に工夫が必要だ。この部分は資料の丸写しではない。 資料では端折られていたので、自分で穴埋めしたのだ。 資料の内容を理解せずに丸写ししているわけではないのだ。 |
ところで同軸ケーブルの場合、信号が伝わる向きは 1つ方向だけを考えればよい。反射波は考える必要がない。 そこで同軸ケーブルの場合の、特性インピーダンスは 以下のように求められる。
| 同軸ケーブルの特性インピーダンス |
|---|
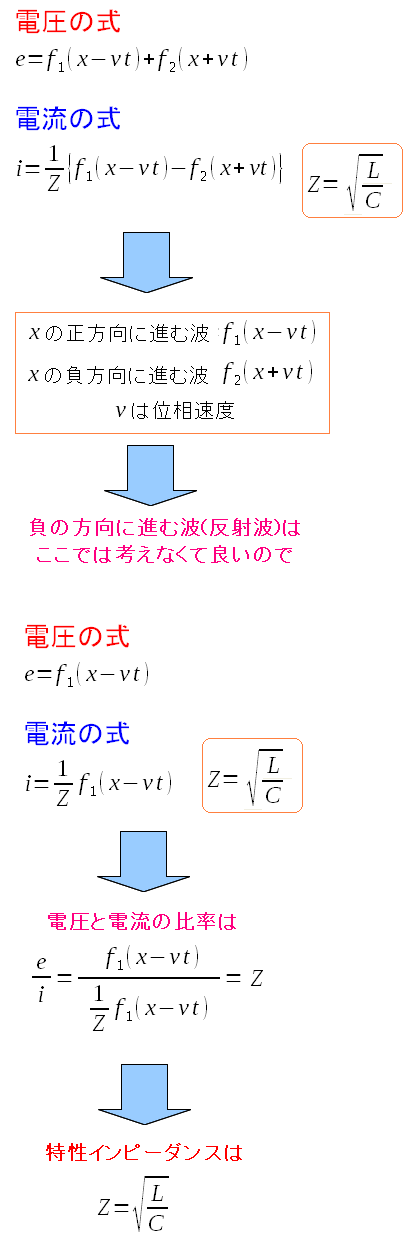 |
| インダクタンスと電気容量だけに依存した物になる。 |
同軸ケーブルの特性インピーダンスの式は、 以下のように表す事がある。
| 同軸ケーブルの特性インピーダンスの式 |
|---|
 |
|
内部導体の内径と、外部導体の内径と 比誘電率の3つの変数で表せるという。 |
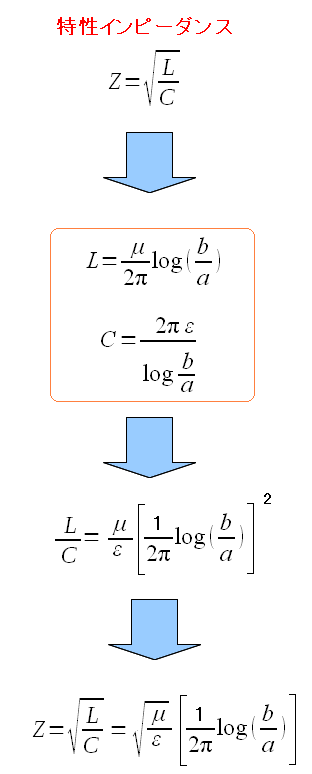
上の式を導いてみる。
| 特性インピーダンスの式を導く |
|---|
 |
|
同軸ケーブルのインダクタンス(L)と電気容量(C)は 既に求めているので、それを代入する。 同軸ケーブル内の絶縁体の誘電率と 導体の透磁率と、内部と外部導体の内径の4つの変数で表せる。 |
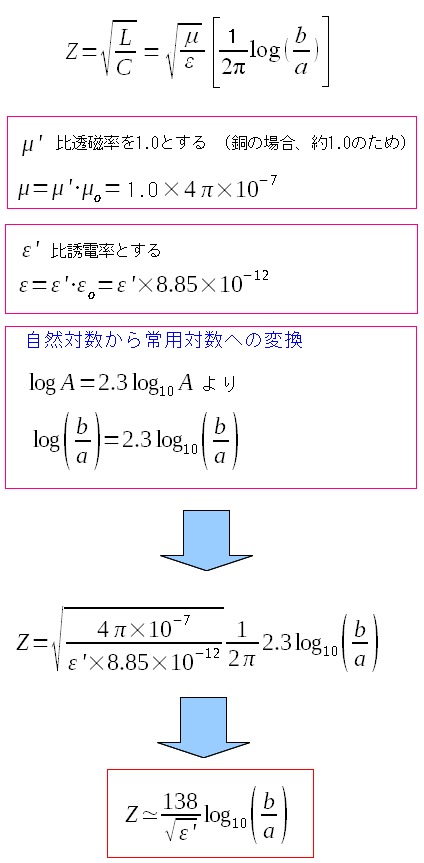
ここから、もう一歩話を進める。
| 銅の比透磁率を「1.0」とする |
|---|
 |
|
導体に使われている銅の比透磁率を「1.0」とする。 そして対数を自然対数から常用対数へ変換する。 すると求めたい式が出てきたのだ。 |
同軸ケーブル内で信号が伝わる速度
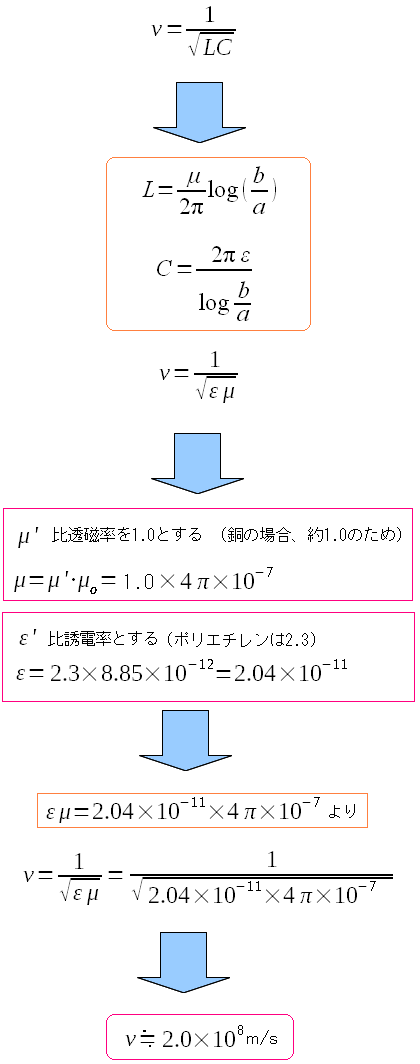
そして同軸ケーブルを伝わる電気信号(波)の速度は 真空中の光速の60%ぐらいと言われている。 そこで実際に、同軸ケーブルを伝わる波(電気信号)の位相速度を求めた見た。
| 同軸ケーブルを伝わる波(電気信号)の位相速度 |
|---|
 |
|
導体に使われている銅の比透磁率を「1.0」とする。 絶縁体に使われているポリエチレンの比誘電率が2.2〜2.4なので 2.3として計算してみた。 すると位相速度は、真空中の光速の66%ぐらいになった。 |
ところで電気信号の速度が、ポリエチレンの影響を受けるのか。
その理由は
電気エネルギーは導線の外を伝わる
からだ。
「システム奮闘記:その105」(電磁気学入門)のポインティングベクトルと
電気エネルギーは電線の外を伝わるで触れたのだが、ここで復習。
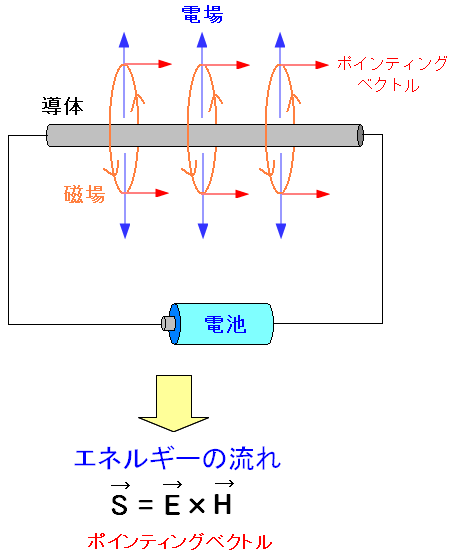
電気のエネルギーの向きと大きさは、ポインティングベクトルで表される。
| ポインティングベクトル |
|---|
 |
|
ポインティングベクトルは、単位体積辺り、単位時間辺りに流れる エネルギー量になるのだ。 電磁波なので、エネルギーは光速(※)で流れていくのだ。 (※注意) ここでの光速とは真空中なら真空での電磁波の速度で 物質中なら物質中の電磁波の速度の事を意味します。 |
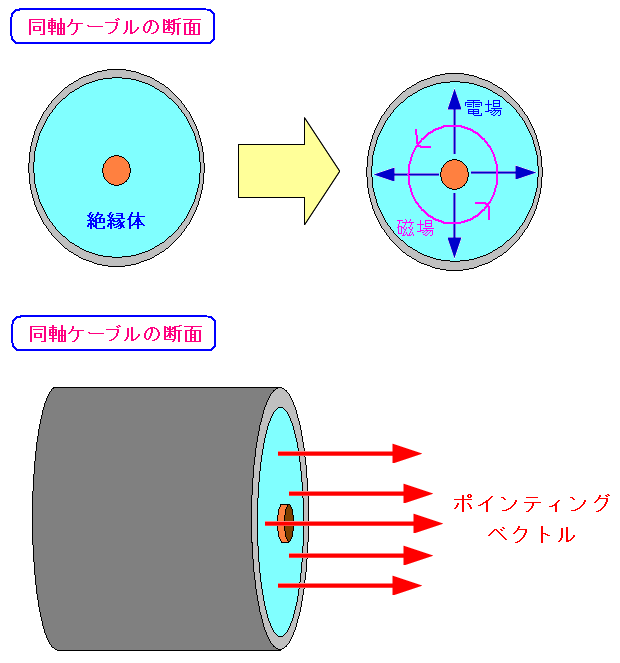
同軸ケーブルでは、どのように電気エネルギーが伝わるのか 見てみる事にする。
| 同軸ケーブルでの電気エネルギーの伝わり方 |
|---|
 |
|
電場も磁場も絶縁体内のみで発生する。 外部導体の電位がゼロのため、内部導体から外部導体の間だけ電位があり そこに電場が発生する。 内部導体が電流の行き方向。外部導体が帰り方向だ。 お互い電流が反対方向に流れている。 アンペールの法則により、外部導体の外では、磁場がゼロになるのだ。 電気エネルギーは絶縁体内を伝わっている事になる。 絶縁体内での電磁波は、前述している通り、絶縁体の比誘電率に影響される。 そのため真空中の光速よりも遅くなるのだ。 |
同軸ケーブルを伝わる信号が、光速の60%ぐらいになるのがわかった。 ポインティングベクトルを使うと、すっきりした説明ができるのだ。
終端抵抗
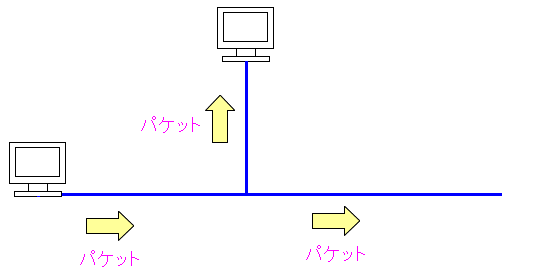
同軸ケーブルで通信を行う場合、同軸ケーブルの末端に終端抵抗が必要になる。 それは同軸ケーブルの末端に到達した電気信号が反射させないようにするためだという。
| 同軸ケーブルの端に終端抵抗をつけない場合 |
|---|
 |
|
パソコンからパケットが出る。 どの経路にも信号が波として伝わっていく。 |
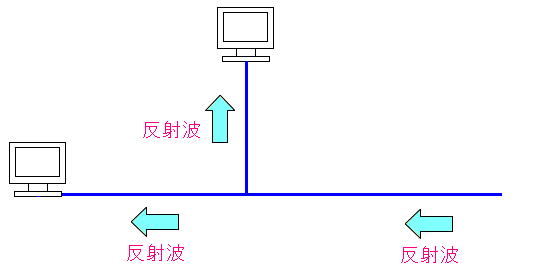
そして同軸ケーブルの端に信号波が到達すると反射するのだ。
| 同軸ケーブルの端に信号波が到達すると反射する |
|---|
 |
|
同軸ケーブルの端では信号波が反射するため、反射波が発生する。 これが悪さしたりするのだ。 |
そこで反射波が発生しないように、終端抵抗をつける。
| 終端抵抗の役目 |
|---|
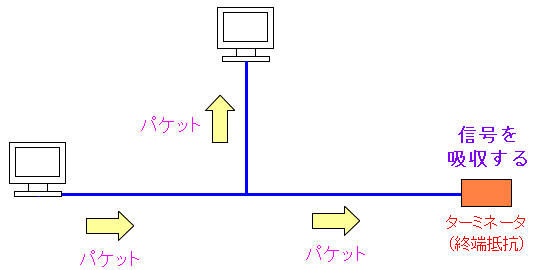 |
| 終端抵抗の部分で信号波を吸収するため、反射波が発生しなくなる。 |
ところで・・・ なんで反射波が発生しないねん!! なのだ。 そこで調べてみることにした。 計装豆知識|終端抵抗 だが反射波を防ぐと書いているのだ・・・ なんでか、わからへん!! なのだ。 色々、調べていくうちに、特性インピーダンスの話を知らないと理解できない話なのだ。 送線路理論の基礎(PDF) ところで終端抵抗がない場合、反射波の問題が出てくる。 そこで以下の回路を考えてみる。
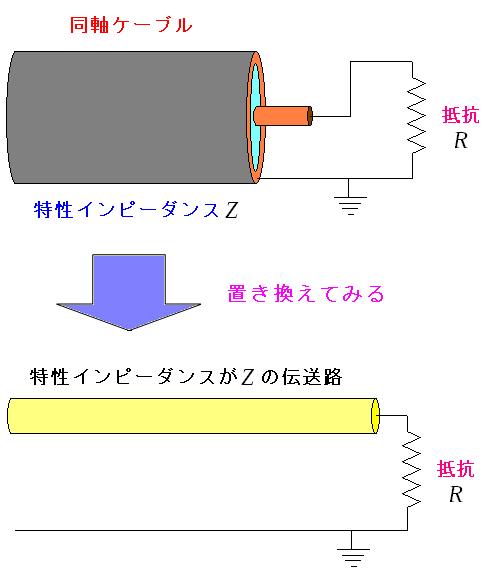
| 同軸ケーブルに抵抗をつけた場合 |
|---|
 |
|
同軸ケーブルの内部導体と外部導体の間に抵抗をつけた回路を考えてみる。 同軸ケーブルだと絵を描くのが大変なので、わかりやすくするため 特性インピーダンスZの伝送路と置き換えてみる。 |
特定インピーダンスとは
伝送路を通る信号の電圧と電流の比率
だった。
そこで、同軸ケーブルの末端につけた抵抗(R)が、
特性インピーダンスと同じ大きさだった場合を見てみる。
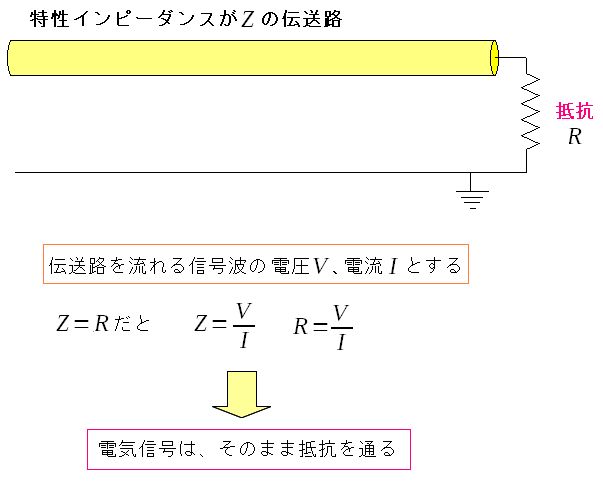
| 抵抗が、特性インピーダンスと同じ大きさだった場合 |
|---|
 |
|
同軸ケーブル内を流れる電圧と電流の関係式は 「電圧=電流×特性インピーダンス」になる。 もし、同軸ケーブルの端っこに「電圧=電流×抵抗」が成り立つ 抵抗をつけたら、そのまま電気が抵抗に向かって流れる。 電気エネルギーは抵抗で熱エネルギーに変換されるのだ。 |
だが、特定インピーダンスと抵抗の値が異なる場合はどうなるのか?
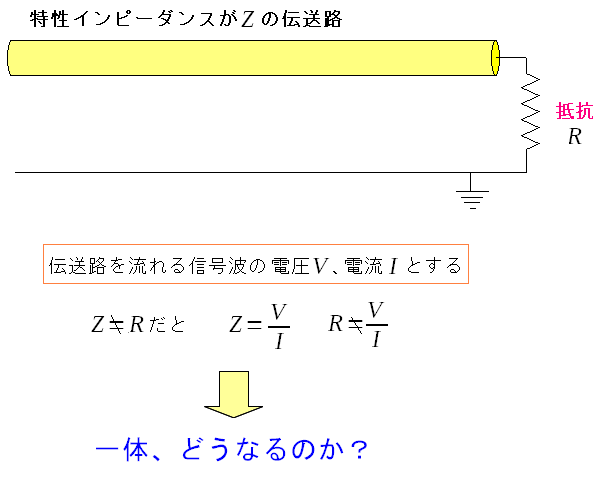
| 特定インピーダンスと抵抗の値が異なる場合 |
|---|
 |
|
伝送路で流れる電圧と電流が、抵抗の部分で「電圧=電流×抵抗」が 成り立たなくなる。 |
この場合・・・
伝送路と抵抗との境界部分で反射波が起こる
というのだ。
そこで進行波の電圧と電流。反射波の電圧と電流。
抵抗を流れる電流を求めてみる。
| それぞれの電圧・電流を求めてみる |
|---|
 |
| それぞれの電圧・電流の式が求まった。 |
まずは抵抗(R)が無限大の場合を見てみる。
| 抵抗(R)が無限大の場合 |
|---|
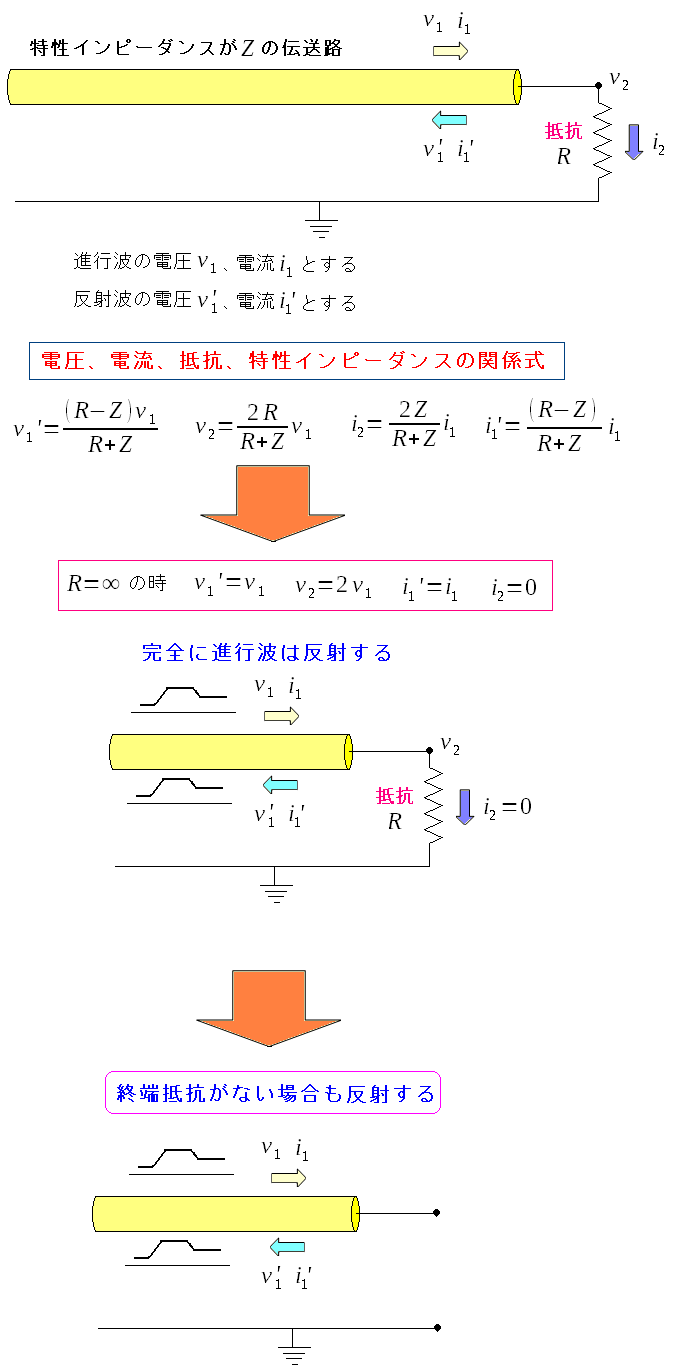 |
|
抵抗(R)が無限大の場合、進行波は100%反射してしまう。 反射波が発生してしまうのだ。 抵抗がない場合は、抵抗が無限大と同じになるため 同軸ケーブルで終端抵抗をつけないと、反射波が発生する事になる。 |
反対に抵抗がゼロの場合を見てみる。
| 抵抗がゼロの場合 |
|---|
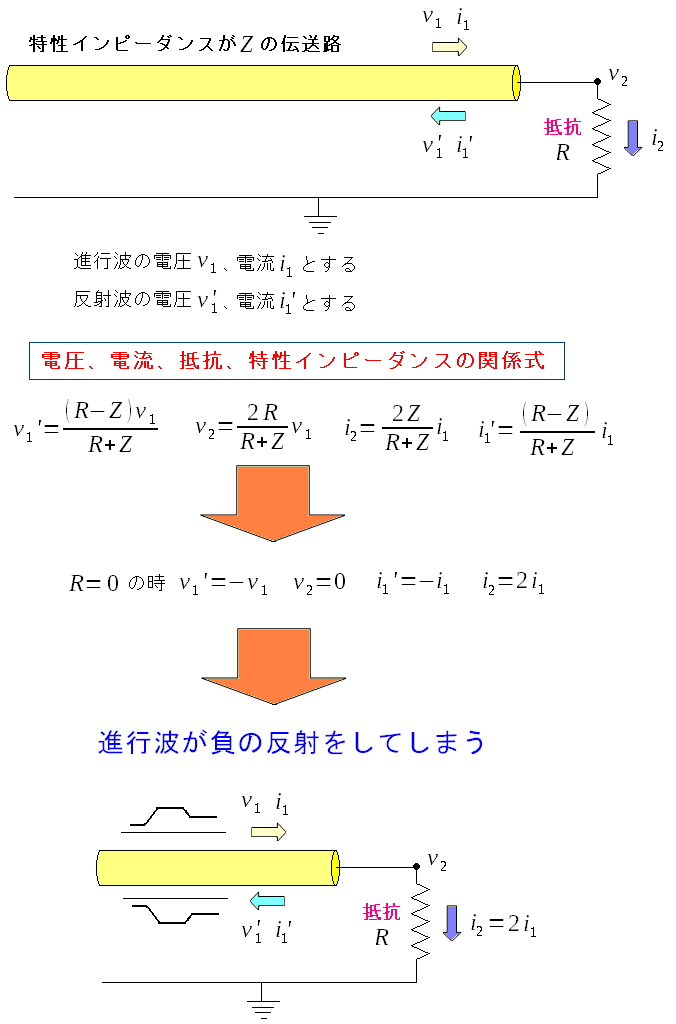 |
|
抵抗に流れる電流が2倍になるだけでなく 負の値の反射波が発生する。 |
特性インピーダンスと終端抵抗が一致していないと 反射波が起こる というのだ。 隣り合う線の特性インピーダンスの不一致、 もしくは特性インピーダンスと、その隣につけられた抵抗との不一致を インピーダンスの不整合 というのだ。 インピーダンス不整合は、回路だけではない。 病院でお腹などを検査するための、超音波診断装置でも出てくる話なのだ。 超音波診断の時、ゼリー状の物を塗る理由は、インピーダンスの不整合をなくすためだという。 No.67 電子回路のインピーダンス・マッチングとは?|電気と磁気の?(はてな)館|TDK Techno Magazine ゼリー状の物を塗る理由が知ったのだ。
| LAN入門:目次 | |
|---|---|
| ストレートケーブルとクロスケーブル | LANケーブルのストレートタイプとクロスタイプの違いを書きました。 |
| リピーターハブとスイッチングハブ |
リピーターハブとスイッチングハブの違いと、全二重通信と半二重通信の話です。 10Base-T以降では、パケット衝突は、実は擬似衝突などを書いています。 |
| 社内LANの調査 | 2005年に、ブラックボックス化した社内LANを解明した話です。 |
| オートネゴーシエーション |
10Base-T、100Base-TX、1000Base-Tなどが混在する環境で どうやって通信制御を行っているのか その仕組みを書きました。 |
| LANケーブルの規格 CAT(カテゴリー) | LANケーブルの規格のCAT(カテゴリー)の違いを書きました。 |
| データ送信とデジタル信号の符号化 |
LANケーブルを信号が伝わる際、どうやってデータ送信をしているのか。 デジタル信号の周波数を抑えながら、高速で信号送信する技術を書きました。 10Base-T、100Base-TX、1000Base-Tについて書きました。 |
| データリンク層 |
LAN内のパソコンや通信機器同士の通信はMACアドレスが使われています。 それを司るデータリンク層について書きました。 |
| 表皮効果と近接作用 |
LANケーブル内で起こっている信号減衰の原因が 表皮効果と近接作用である事と LANケーブルの撚り線が、ノイズ対策なのを書きました。 |
| ツイストペアとノイズ対策 |
LANケーブルがツイストペア(撚り線)なのはノイズ対策のためです。 その話を書きました。 |
| 差動回路とノイズ対策 |
LANケーブルは8本あり、データ通信は複線で行っています。 差動回路を使ったノイズ対策の話を書きました。 |
| 同軸ケーブルの仕組み |
昔のLANに使われていた同軸ケーブル。 現在でもテレビのアンテナに接続する線として使われたりしています。 同軸ケーブルの仕組みや特性インピーダンスの話を軽く触れました。 |
| 発振回路 |
クロック信号を作る発振回路の説明です。 簡単なLC型コルピッツ発振回路を使って説明しました。 |