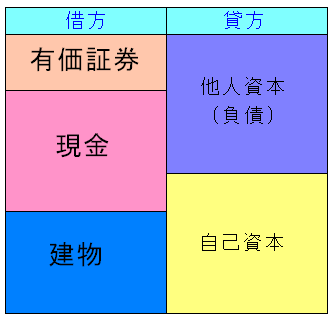
左側の借方は財産目録で、有価証券(株や公債)、土地、建物、現金などがある。
右側の貸方は自分のお金(自己資本)なのか、他人のお金(負債)なのかを表す。
負債の内訳として、銀行から書いていたら「借入金」だったり
備品などをツケで買っていたら、購入先からの借金しているとみなして
「買掛金」という名目で負債に入れる。
システム奮闘記:その108
(2017年10月10日に掲載)
在庫管理の難しさ
在庫管理 簡単なようで実は難しい分野だ。 仕入担当者は常に上層部から 必要以上の在庫を持つな だけど欠品をなくせ という無理難題を突きつけられていた。 欠品をすると、他から商品を買おうとする顧客が出てくる。 機会の損失を出さないよう、常に在庫があるのが望ましい。 だが、大量に在庫を抱えると問題を抱えてしまう。
| 在庫を抱えた場合に発生する問題 | |
|---|---|
| 売れ残り | 売れ残った場合、在庫の山になる。 |
| 保管場所 | 保管する場所の確保が問題になる。 小さい商品なら良いが、大きな商品だと置き場の問題が出てくる。 自社の倉庫ならまだしも、置き場がなく、貸し倉庫に保管すると 保管料がかかるため、経費削減という観点では在庫は少ない方が良いのだ。 |
だが、簿記を知っていたら、もっと厄介な問題が見えてくる。
財務面から見た在庫問題
在庫を可能な限り持たないようにする。 財務面で見ると、その理由が見えてくる。
| 財務面で見た在庫を抱える問題点 | |
|---|---|
| 売れ残り | 売れ残った場合、在庫の山になる。 安易に廃棄処分できない 廃棄処分した時、損失として計上するのだが 利益圧縮と思われる場合があるので、廃棄処分する際は 証拠写真を撮って、税務署に提出する必要があったりする。 量販店などで、原価割れしても在庫処分セールを行うのは 在庫資産を少しでも現金化するのと、廃棄処分を避ける事で 廃棄処分費用の削減と、税務署への説明が不要になるためだ。 |
| 税金がかかる |
仕入れた段階では出費にならず在庫資産として計上される。 そのため仕入れた商品が売れない限り、仕入れた金額分は 利益扱いのため、それに税金がかかる事になる。 |
財務の視点から見ると、在庫は必要最低限にするのが良いのだ。 企業の帳簿をつける際、大きくわけて2種類の帳簿がある。 財産の状態を表す貸借対照表 収支の状態を表す損益計算書 がある。 これを読んでいる人の中には簿記の知識がない人もいるので まずは貸借対照表(BS:バランスシート)がどういう物か簡単に説明する。
| 貸借対照表(BS) |
|---|
 |
|
財産を表した帳簿だ。 左側の借方は財産目録で、有価証券(株や公債)、土地、建物、現金などがある。 右側の貸方は自分のお金(自己資本)なのか、他人のお金(負債)なのかを表す。 負債の内訳として、銀行から書いていたら「借入金」だったり 備品などをツケで買っていたら、購入先からの借金しているとみなして 「買掛金」という名目で負債に入れる。 |
商品を仕入れて在庫にした場合
棚卸資産
となり、財産の1つとして数えられる。
まずは手持ち現金で仕入れた場合、貸借対照表がどう変化するのか見てみる。
| 手持ち現金で仕入れた場合 |
|---|
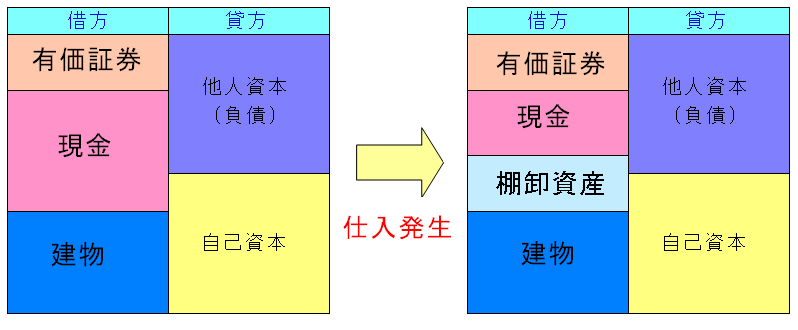 |
| 貸方(財産目録)の現金が減った分、棚卸資産が増える。 |
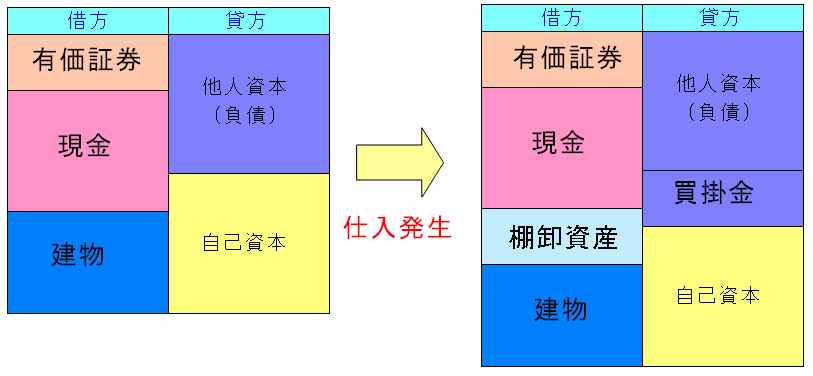
次にツケで商品を仕入れた場合、貸借対照表がどう変化するのか見てみる。
| ツケで仕入れた場合 |
|---|
 |
|
貸方(財産目録)に在庫(棚卸資産)が加わる。 ツケで仕入れたため、棚卸資産の購入費用分、貸方の負債が増える。 この場合、ツケは借金と同じなので他人資産の区分される。 「買掛金」という勘定科目になる。 |
家計簿の感覚だと、物を購入した場合、出費扱いになるが 企業会計の場合だと・・・ 現金資産が棚卸在庫に変わるだけで 仕入は出費にはならへん!! のだ。在庫と税金問題
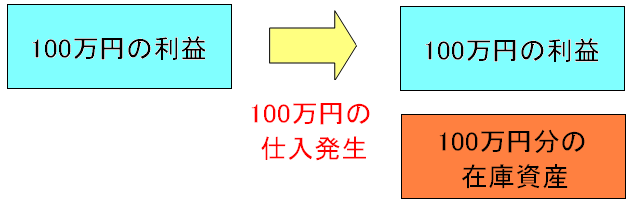
仕入は出費にならない。 そのため100万円の利益が出てる時に、100万円分仕入れても 利益は100万円のまま になる。
| 100万円仕入れても出費にならず、在庫資産になる |
|---|
 |
|
100万円、商品を仕入れても出費にならない。 100万円の棚卸資産が増える上、利益は変わらない。 |
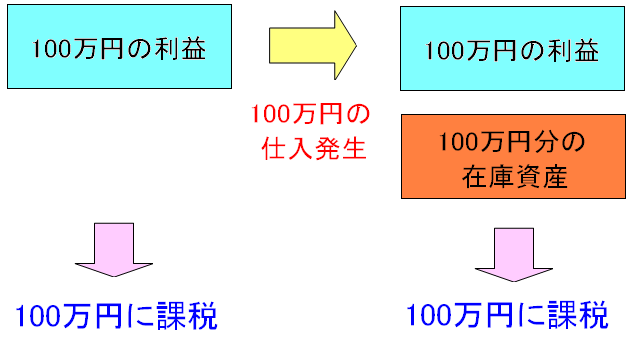
仕入は出費にならないため
税金がかかる
と同じなのだ。
| 仕入があっても税金はかかる |
|---|
 |
|
仕入は出費にならない。 そのため利益が100万円ある状態の課税金額と 100万円の仕入をした後の課税金額は同じになる。 |
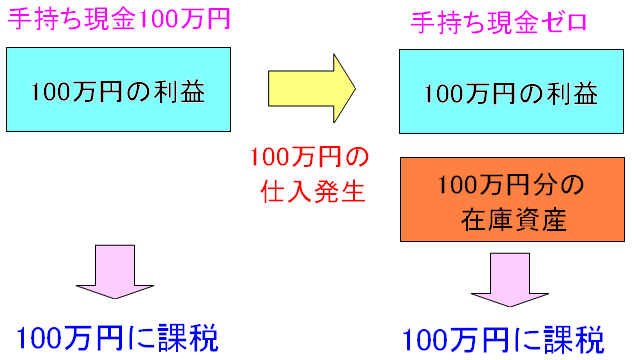
こんな状態だと
利益があっても資金がない
に陥っている状態なのだ。
損益計算書の利益と、実際の手元現金との差異が引き起こす問題だ。
黒字倒産の原因の1つとされている。
| 黒字倒産の仕組み |
|---|
 |
|
損益計算書の利益と、手持ち現金との間に差異があるため 手元に現金がないため、課税されると、税金を払うために 資金調達する必要がある。 この時、誰もお金を貸してくれなければ、企業活動ができなくなり 倒産してしまうのだ。 |
仕入が出費になる場合は、仕入れた商品を販売した時だ。
| 商品を販売して、仕入が出費になる |
|---|
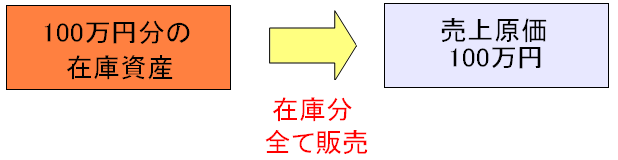 |
| 仕入商品を販売した際、売上原価という科目で出費となる。 |
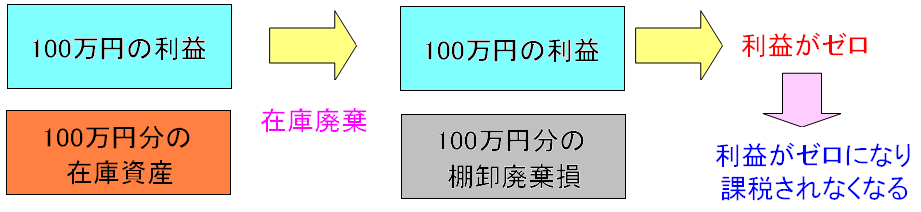
他にも売れ残った商品を廃棄した場合も出費になる。
| 商品を廃棄した場合も出費になる |
|---|
 |
|
棚卸廃棄損という扱いで、出費になる。 だが、これを下手に行うと、税務署から利益圧縮の疑いがかけられる。 そのため在庫分を廃棄する際は、写真撮影して、廃棄した証拠を残すのが 大事とされている。 |
税務署から利益操作を疑われる可能性があるため、安易に在庫を廃棄処分にできない。 そして在庫を廃棄処分するためには費用がかかるため 原価割れでも売ってしまえ!! となる。 原価割れになってでも売ってしまえば、現金化できるからだ。 そして原価割れで売った場合、利益が減るため、税金対策にもなる。 よく街中で売れ残り商品の安売りを行っているのを見かけるが 裏には、廃棄処分するよりも、現金化した方が良いという発想があるのだ。
在庫管理は勘・経験・度胸
上層部から無理難題を課せられている仕入担当者。 だが、発注点管理をするソフトがあるわけでもない上 ましてや発注点予想できるソフトもない。 どうしても・・・ 勘・経験・度胸 で判断せざる得ない状態だ。 巷でよく言われるKKD(勘・経験・度胸)だ。 私自身、KKDを偉そう批判できない。 ネット販売の商品で、一部の商品の在庫は私が管理している。 発注点算出をしているわけでなく、勘と称した物で 適当に発注していたからだ。
在庫管理と統計学
在庫管理。私が入社して間もない頃、ある役員が 在庫管理をなんとかせねば! と言っていた。 当時、新人だったので、何か貢献できないかと考え 書店や図書館などで在庫管理の本を探したら見つかった。 だが書店で在庫管理の本を見たのだが・・・ 統計学なんぞわからへん!! だった。 一応、元・理系なのだが統計学は大の苦手。 だが、20代だったので、元・理系の意地という事で、 図書館で統計学の本を借りて挑戦したものの・・・ あえなく討ち死に だった。
統計学の勉強
2010年から、ある数種類の商品の在庫管理をする事になった。 発注点は、売れ行き状況をみて、感覚で決めていた。 要するに何の根拠もない・・・ 大雑把で適当すぎる発注点算出 だったのだ。 だが、この時は統計学を用いて発注点算出しようとは思わなかった。 理系だったのは20世紀の話。「過去には振り返らない」という開き直りで 統計に再度挑戦という気は起こらなかった。 だが、2013年のある日、在庫管理と発注点の話が出た。 ふと思った。 システム奮闘記のネタに使えるから 統計的手法を取り入れてみよう 苦手な統計。 だが、重い腰を上げて、学生時代、統計学の教科書として使っていた本を取り出す。 「基本統計学」(宮川公男:有斐閣) そして統計学の勉強をする際・・・ 数式の意味はどうでもええ!! 公式を当てはめるだけ 数式の導き方や、数式の意味を理解しようという事は諦めて 単なる道具だと完全に割り切る事にした。
出荷数は1週間ごと
日々の出荷数の変動を見たりすれば良さそうだが・・・ 中小企業だと出荷数が少ないため 統計誤差が大きすぎる という問題がある。 だが、1ヶ月単位で出荷数を集めると、月別の出荷数の比較ができるが 1ヶ月といっても、2月は28日(うるう年は29日)だし、5月は31日ある。 そのため1ヶ月単位で平均値などを見るのも、具合が悪い。 そこで1週間単位に区切って、出荷数を集計する事にした。
正規分布(ガウス分布)
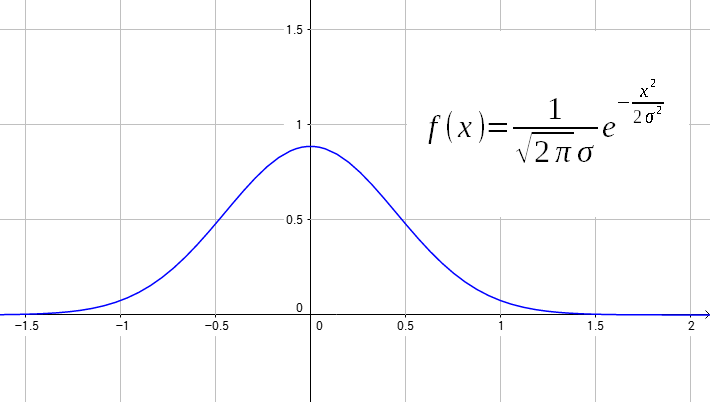
正規分布とは以下のグラフの事だ。
| 正規分布(ガウス分布)のグラフ |
|---|
 |
|
左右対称の山のようなグラフなのが特徴だ。 グラフの意味は、中心が発生頻度が高く、両端ほど発生頻度が低いという事だ。 数式にあるσは標準偏差の意味で、ここの値を変えると、グラフの広がりが変わる。 標準偏差は、ばらつきの度合いを表わします。後述しています。 |
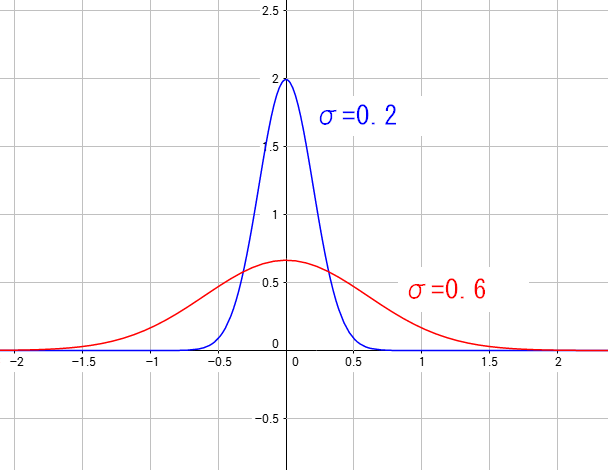
ここで標準偏差の値を変えると、正規分布のグラフは以下のように変わる。
| 標準偏差の値を変えてみる |
|---|
 |
|
青いのがσ=0.2の時で、急に高くなる山になっている。 赤いのがσ=0.6の時で、緩やかな山になっている。 後述しているが、σの値が大きいほど、ばらつきが大きい事をあらわす。 |
この正規分布は、工業製品の品質を見る上で使われる事が多い。
例えば、長さ100cmの棒を生産した事を考える。
寸分の狂いもなく100cmの棒を作るのは不可能だ。
どうしても数ミリ、場合によっては数センチの誤差が生じる事がある。
誤差の頻度を見る
ために正規分布が使われる。
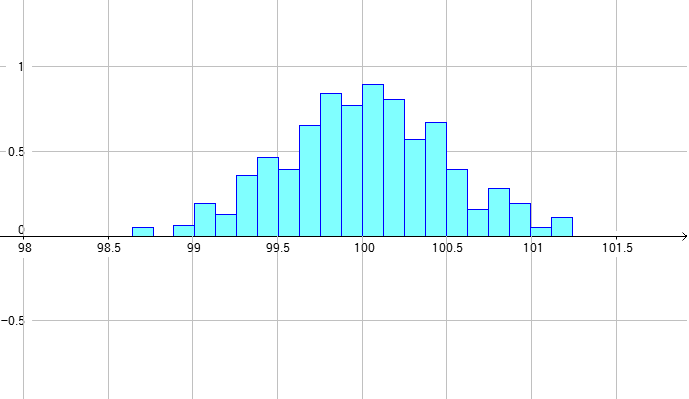
| 100cmの棒を生産した時の誤差の頻度(例) |
|---|
 |
|
100cmの棒を生産した際、どうしても製品に、ばらつきが出るため 上図のような感じになる。 そこで、このばらつきが、どの程度なのかを見たりするために正規分布が使われる。 |
そこでデータ処理をした後で導いた正規分布の関数を当てはめると こんな感じになるというのだ。
| データ分布と正規分布を重ね合わせた物 |
|---|
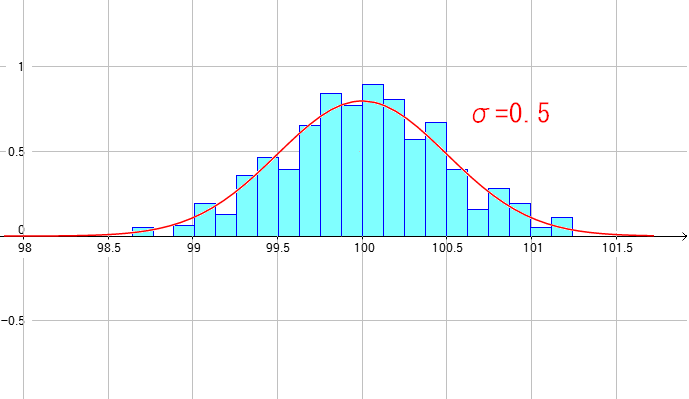 |
| ばらつきの度合いをグラフ化したものが正規分布グラフになる。 |
正規分布のグラフを描く関数の事を 確率密度関数 という。 ここでは確率密度関数とは何かは触れない。 いつもと違い、不親切で投げやりな書き方をしている。 なぜなら・・・ 最後まで読むと、投げやりの理由がわかるのだ!! と完全に投げやりの内容なのだ。
標準偏差
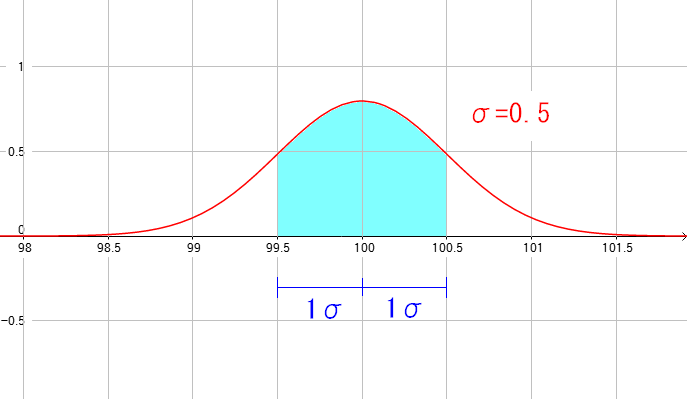
ばらつきの度合いを表す標準偏差。 σ=0.5で考える。なぜσの求め方を書かないかといえば 先にσの意味を説明した方がわかりやすい と勝手に思ったからなのだ。 なので、ここでは天下り的に、σの値を0.5として考える事にした。 100cmの棒を生産した際、できた製品を計った結果 標準偏差の値(σ)が0.5だった場合を考える。 標準偏差のσの使い方は以下のようになる。
| 標準偏差(σ)とは |
|---|
 |
|
上図を例にして、σ=0.5の場合、100cmを中心に0.5の幅をもたせた範囲になる。 この範囲を1σという。この範囲に入るのは全体の68%になる。 |
つまり、1σといえば
測定した物の68%が入る範囲
なのだ。
積分すればわかるのだ。
2σの場合は以下のようになる。
| 標準偏差の2σとは |
|---|
 |
|
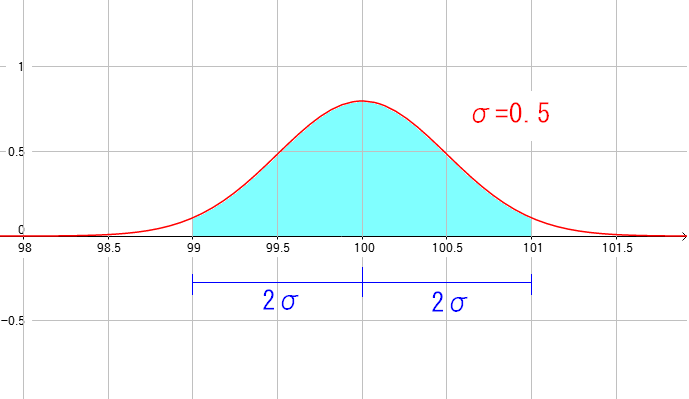
上図を例にして、σ=0.5の場合、100cmを中心に1.0の幅をもたせた範囲になる。 この範囲を2σという。この範囲に入るのは全体の95%になる。 |
つまり、2σといえば
測定した物の95%が入る範囲
なのだ。
3σの場合は以下のようになる。
| 標準偏差の3σとは |
|---|
 |
|
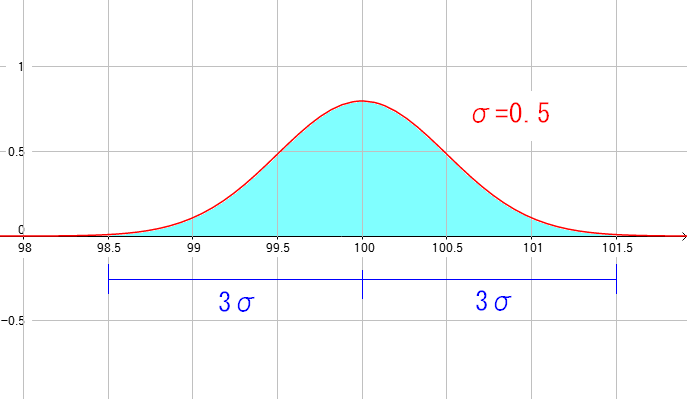
上図を例にして、σ=0.5の場合、100cmを中心に1.5の幅をもたせた範囲になる。 この範囲を3σという。この範囲に入るのは全体の99%になる。 |
つまり、3σといえば 測定した物の99%が入る範囲 なのだ。真値がわかっている時の標準偏差の求め方
真値とは字の如く、正しい値の事だ。 工業製品で、100cmの棒を作りたいと思った時、真値は100cmになる。 実際に生産された製品の長さと真値を比較して、 どれくらいの、ばらつきになっているのかを見てみる。 どうやって、ばらつきを表す標準偏差(σ)を求めるのか。 ここから解説しようと格好つけて書きたい所だが 実際には・・・ 公式丸暗記、当てはめ で行う事にした。 まずは分散を求める。これは標準偏差の2乗の値になる。
| 分散(標準偏差の2乗)を求める |
|---|
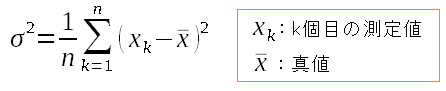 |
| 製造した物がK個あった場合、上の式になる。 |
なぜ、分散が上の式なるのかは
わからへん!!
とアッサリ書いてしまう。
さて、分散が求まったので、分散の平方根をとれば標準偏差になる。
| 標準偏差の式 |
|---|
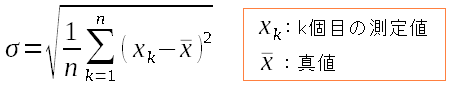 |
| 製造した物がK個あった場合、上の式になる。 |
公式は簡単。求めるのは簡単。 だけど、なんでこんな式になるのかは 難しくて、わからへん!!真値がわからない場合
工業製品の場合、真値は定まっていた。 だが、未知の物の観測や実験をした場合、真値は不明だ。 その場合・・・ 真値を知りたい場合はどうするねん? となる。 観測や実験した際に出てきた値が全て真値だったら良いのだが 観測機器や測定機器の精度が高くても、測定誤差が出てくるため 結果だけでは真値がわからへん!! となってしまう。 そこで・・・ 真値の場所を推定してしまえ!! となる。
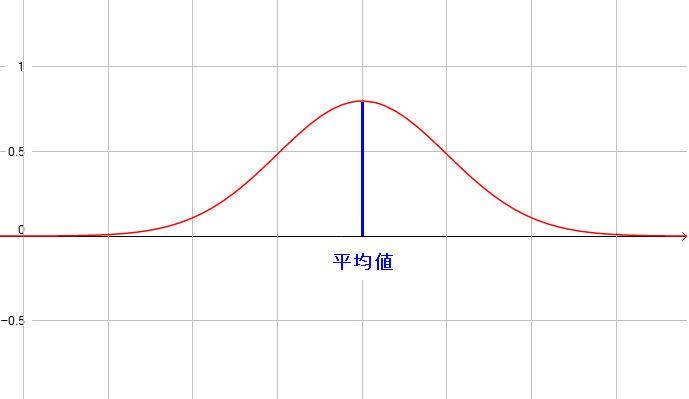
| 平均値を使って正規分布を描く |
|---|
 |
|
真値は不明だが、平均値は求められるため、平均値を中心とした 正規分布のグラフを使う。 |
そして分散は以下のように求める。これは標準偏差の2乗の値になる。
| 分散(標準偏差の2乗)を求める |
|---|
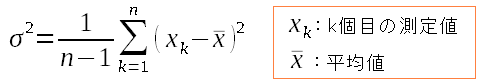 |
| 真値の代わりに、平均値が入る。 |
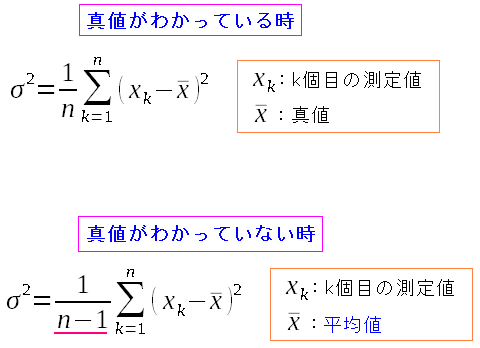
真値がわかっている場合の式と少し違う。 比較してみる。
| 真値がわかっている場合と、わからない場合の違い |
|---|
 |
|
真値がわかっている場合は、測定した個数で割っている。 真値が不明な場合は、測定数から1引いた数字で割っている。 |
一体、何でやねん!! となる。 ところで真値の場合、独立した値なのだ。 だが、平均値の場合を考えてみると・・・ 平均値は測定値に依存した値 なのだ。 そのため「各測定値から平均値を引いた値」が独立変数でなくなるため 1個減らした(n-1)にしてしまうのだ わかったような、わからんような説明なのだ。
| 敢えて説明は端折ります |
|---|
|
独立変数でないから、n-1にする話。 統計学の入門書などで、自由度が1個減るという説明があったりする。 だが、なぜ自由度が1減るのかに関して、納得できる説明を書いている 入門書はない。本が悪いのではない。 キチンと説明するためには、高度すぎる数学が必要だからだ。 |
ところで、この時の正規分布の意味を考える。 真値がわかっている場合とは、異なる意味になる。
| 正規分布の意味 | |
|---|---|
| 真値がわかっている場合 | 誤差の発生確率を表す |
| 真値がわからない場合 | 真値がある確率を表す |
なので・・・
真値の推定
というわけなのだ。
図にすると以下のようになる。
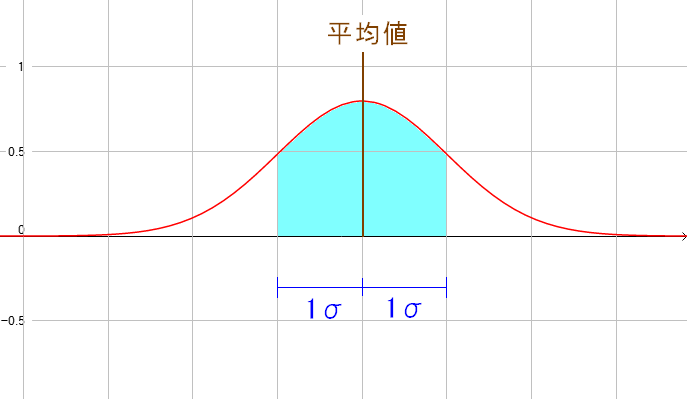
| 1σの範囲とは |
|---|
 |
|
平均値から1σの範囲とは、真値が入る確率が66%の範囲だ。 真値は平均値に近いという発想があると思うのだが 深くは立ち入れない。難しくて、とても立ち入れないのだ。 |
そして2σの範囲を見る。
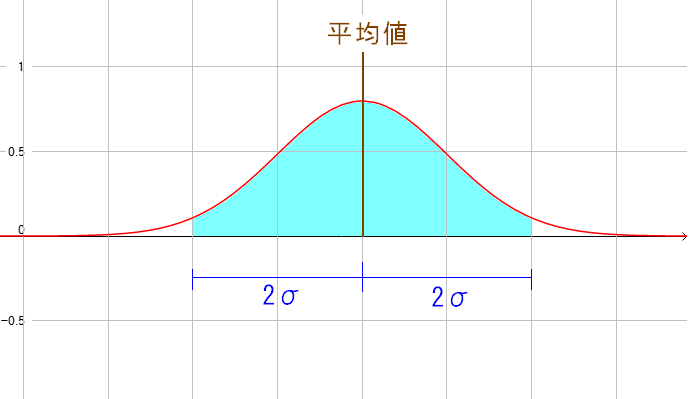
| 2σの範囲とは |
|---|
 |
|
平均値から2σの範囲とは、真値が入る確率が95%の範囲だ。 よほど測定機器にクセがあったり、測定の際、悪条件でない限り この辺りで収まってくれるであろう範囲の値かもしれない。 |
そして3σの範囲を見てみる。
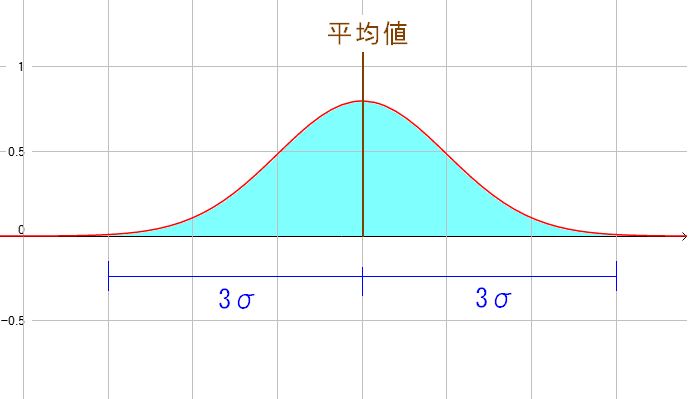
| 3σの範囲とは |
|---|
 |
|
平均値から3σの範囲とは、真値が入る確率が99%の範囲だ。 この外に真値があったら、測定機器そのものがおかしいと疑っても良いかも。 ただ、測定機器がおかしいかどうかの判定は難しい。 あらかじめ真値がわかっているなら別だが、未知の値の場合 何が真値なのかが、わからないため、測定値からでた推定を信じるしかない。 |
出荷量の算出
真値がわからない場合、真値の推定に正規分布を使う事がわかった。 そこで出荷量の算出ができないかと考えた。 2013年1月から6月までの半年間の期間、 出荷量の多い商品Aで見てみる事にした。 出荷量が多いとはいえ、中小企業。 1日ごとだと変動が大きすぎるため、1週間ごとに区切って、 商品の出荷量を計算し、その分布を求める事にした。
| 半年間の商品Aの出荷量(1週間単位) |
|---|
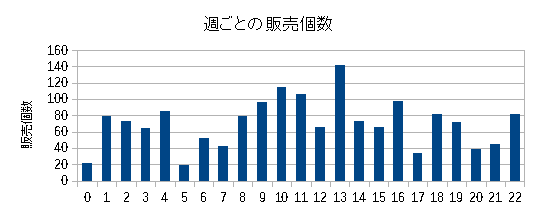 |
| これだけだと出荷量の推移が見れるのだが傾向は見えてこない。 |
そこで平均値、標準偏差を求める事にした。 平均出荷数 71個 標準偏差 30個 正規分布に当てはめてみると以下のようになる。
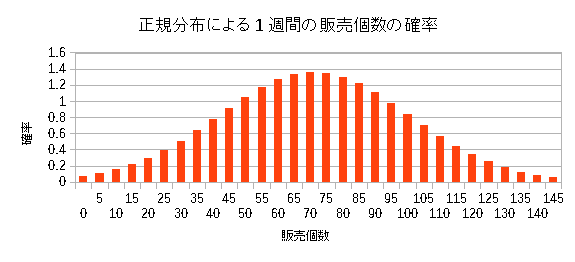
| 商品Aの出荷量の頻度分布 |
|---|
 |
|
求まった平均値、標準偏差から、商品Aの出荷量の頻度分布として 正規分布のグラフにしてみた。 |
そして実際の出荷数と、その頻度を見てみる。
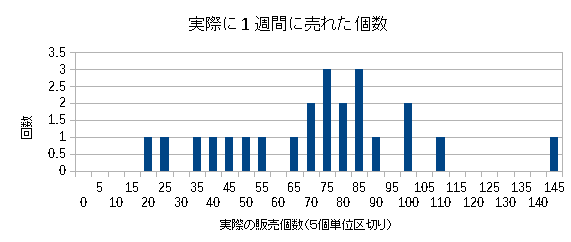
| 商品Aの出荷数と、その頻度 |
|---|
 |
|
正規分布に似ていなくもないが、やや無理があるように思える。 出荷数に真値も何もないため、出荷数が正規分布に従うとは限らないのだが この時は、そんな事に気づかず、正規分布に従わないのはなぜかと思ったりした。 |
もう1度、1週間の出荷量と、標準偏差を見てみる。
| 商品Aの出荷量(1週間)の平均値と標準偏差 | |||
|---|---|---|---|
| 平均値 | 71個 | 標準偏差 | 30個 |
| 読み取った事 |
平均が71個なので、1週間の出荷数のうち 41〜101個の範囲(1σ)の収まるの確率が66%。 11〜131個の範囲(2σ)の収まるの確率が95%と考えた。 | ||
極力、欠品をなくしたいと考えた私は、最大出荷数量を 2σの範囲の出荷量で考えた。 その場合だと1週間の最大出荷量は131個になる。 さて、発注点を求めるのだが、大事なのは 仕入先へ商品の発注してから、入庫するまでの期間を考える必要がある。
| 仕入先へ商品の発注してから、入庫するまでの期間 |
|---|
 |
|
発注から入庫までの期間は商品によっても異なる上 同じ商品でも、仕入先の在庫状況などによっても異なる。 |
そして仕入先へ発注してから商品が入庫するまでの間 在庫分の商品が出荷されるのかを考える必要がある。
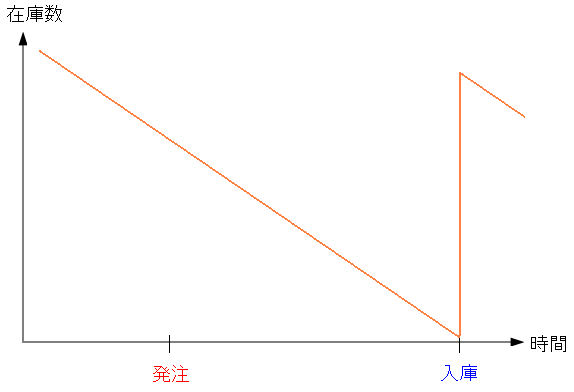
| 発注・入庫までの期間に、出荷される量を考える |
|---|
 |
|
仕入先に商品の発注した後も、在庫分は売れていくため、在庫が減少する。 発注・入庫までの期間、どれくらい在庫があれば大丈夫なのかを求める必要がある。 |
商品Aについては、発注から入庫までの期間を1週間と仮定した。 そして1週間の出荷量で、2σの範囲での最大出荷量は131個だった。 そこで発注点は、以下のように考えた。
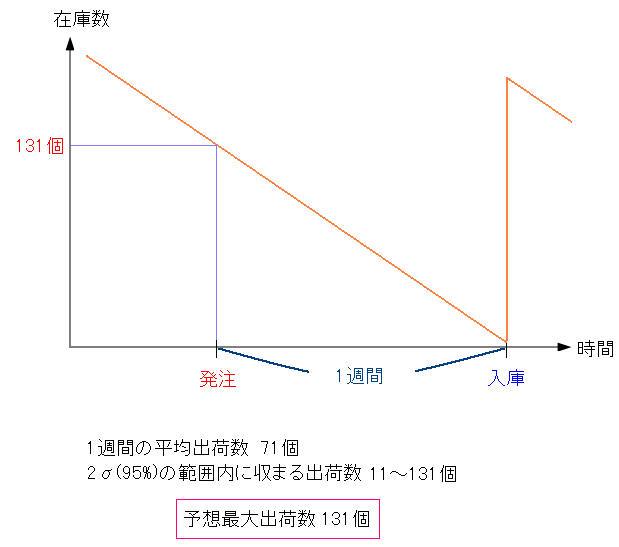
| 商品Aの発注点を算出 |
|---|
 |
|
1週間での最大出荷量が131個。 発注から入庫までの期間を1週間と考えた場合 在庫が131個以上あれば、在庫切れの危険性が避けられる。 そこで商品Aの場合、発注点を131個と設定した。 |
この事から、商品Aの場合の発注点は 在庫数が131個を割り込んだ時 に決めたのだ。
ポアソン分布
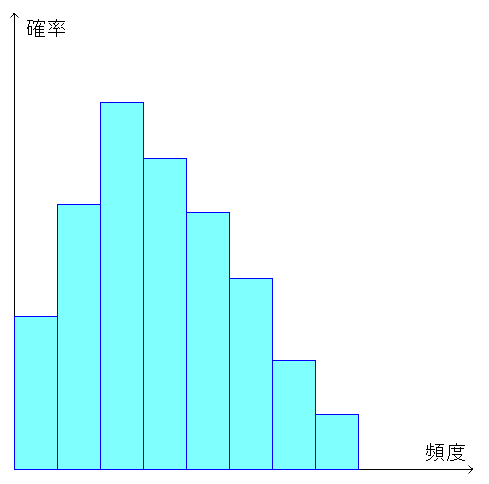
出荷数の少ない商品になると、正規分布が使えない。 その場合は・・・ ポアソン分布 を使う。 ポアソン分布とは、どんな分布なのか図にしてみる。
| ポアソン分布 |
|---|
 |
|
発生頻度が少ない(0に近い)場合、上図のような 発生数と確率のグラフになる。 |
ポアソン分布の場合、以下の数式で表される。
| ポアソン分布での確率分布の式 |
|---|
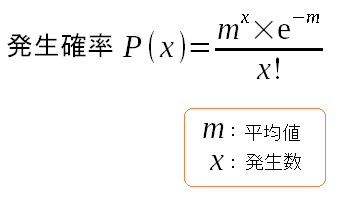 |
|
正規分布の式と違い、標準偏差ではなく、平均値を使った数式になっている。 ポアソン分布の場合、分散(標準偏差の2乗)は、平均値と同じ値なのだ。 |
ポアソン分布での確率分布の公式は、二項分布の式から 導く事ができるのだが・・・ 確率分布の導き方は省略 とする。 いつものシステム奮闘記と違い、手抜き丸出しの内容。 だが、事情はあとで説明しているが 付け刃での確率・統計の勉強は無駄 がわかっているからだ。 さて、出荷数の少ない商品Bについて見てみることにした。
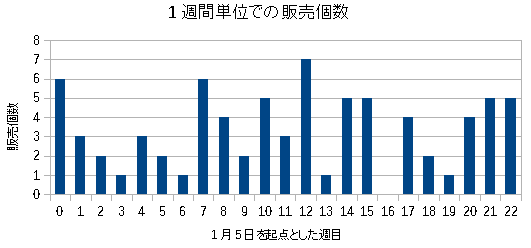
| 商品Bの1週間ごとの出荷数量 |
|---|
 |
|
多い時で7個、少ない時では0個だ。 ポアソン分布が当てはまると考えた。 |
1週間の出荷量の平均値と標準偏差を見てみる。
| 商品Bの出荷量(1週間)の平均値と標準偏差 | |||
|---|---|---|---|
| 平均値 | 3.3個 | 標準偏差 | 1.8個 |
| 読み取った事 |
平均が3.3個なので、1週間の出荷数のうち 1〜5個の範囲(1σ)の収まるの確率が66%。 0〜7個の範囲(2σ)の収まるの確率が95%と考えた。 | ||
そこで実際に平均値を確率分布の式に当てはめてみた。
| 求めた商品Bの確率分布(ポアソン分布) |
|---|
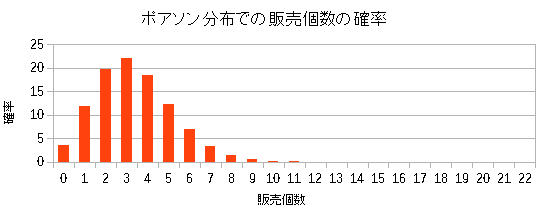 |
| 出荷数3のところで最大になっている。 |
実際の頻度分布を見てみた。
| 商品Bの出荷数と頻度の分布 |
|---|
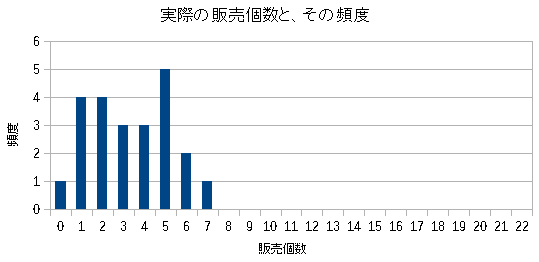 |
| ポアソン分布に少し似ている感じがする。 |
この時、出荷数量の分布で、2σの範囲が0個から7個だ。
発注してから入庫するまでの期間を1週間とした場合
発注点は7個
にすれば良いのだ。
だが、商品Bのような、比較的、出荷数量の頻度分布が
ポアソン分布に従う場合は、少なかったりする。
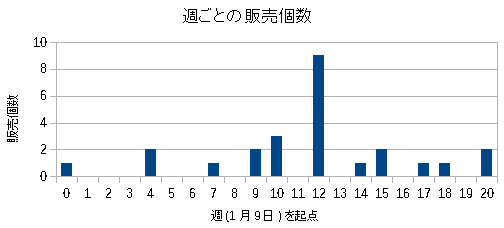
| 商品Cの1週間ごとの出荷数量 |
|---|
 |
|
多い時で9個、少ない時では0個だ。 出荷数が安定していない商品だ。 |
1週間の出荷量の平均値と標準偏差を見てみる。
| 商品Cの出荷量(1週間)の平均値と標準偏差 | |||
|---|---|---|---|
| 平均値 | 1.2個 | 標準偏差 | 1.1個 |
| 読み取った事 |
平均が3.3個なので、1週間の出荷数のうち 0〜3個の範囲(1σ)の収まるの確率が66%。 0〜4個の範囲(2σ)の収まるの確率が95%と考えた。 | ||
そこで実際に平均値を確率分布の式に当てはめてみた。
| 求めた商品Cの確率分布(ポアソン分布) |
|---|
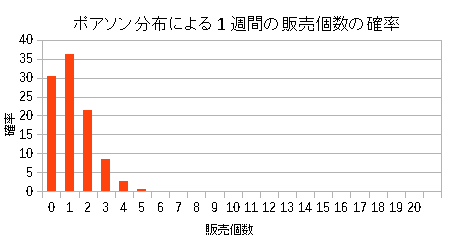 |
| 出荷数1のところで最大になっている。 |
実際の頻度分布を見てみた。
| 商品Cの出荷数と頻度の分布 |
|---|
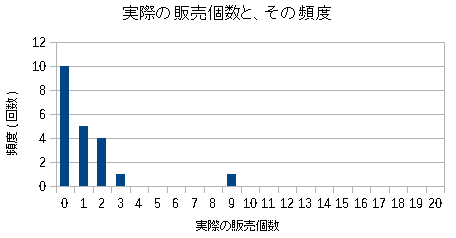 |
| ポアソン分布に似ていない |
出荷数が変則的な商品
出荷数が変則的な商品もある。 商品Dがある。4個セットで販売している。 でも、バラ売りもしている。
| 商品Dについて |
|---|
 |
|
通常、4枚セットで販売していて、お客さんも大抵、4枚買う。 でも、バラ売りもしているため、時々、1枚だけ買うお客さんもいる。 2枚、3枚購入というお客さんは、滅多にいない。 |
この場合、出荷の傾向はつかめにくいし、需要予測は困難だ。 それでも商品Dの出荷量の推移を見てみた。
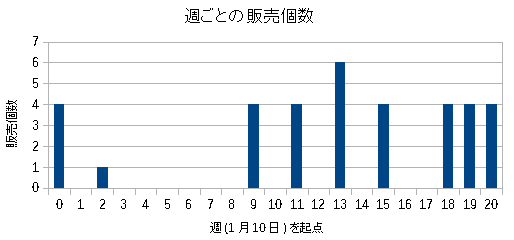
| 商品Dの1週間ごとの出荷数量 |
|---|
 |
|
多い時で9個、少ない時では0個だ。 出荷数が安定していない商品だ。 |
1週間の出荷量の平均値と標準偏差を見てみる。
| 商品Dの出荷量(1週間)の平均値と標準偏差 | |||
|---|---|---|---|
| 平均値 | 1.7個 | 標準偏差 | 1.7個 |
| 読み取った事 | ポアソン分布で見る事に意味がなさそうに思えた | ||
そこで実際に平均値を確率分布の式に当てはめてみた。
| 求めた商品Dの確率分布(ポアソン分布) |
|---|
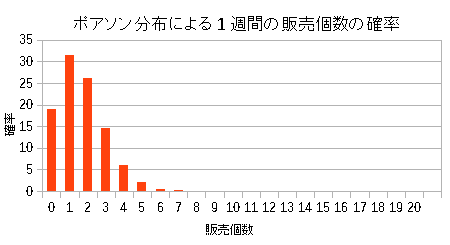 |
| 出荷数1のところで最大になっている。 |
実際の頻度分布を見てみた。
| 商品Dの出荷数と頻度の分布 |
|---|
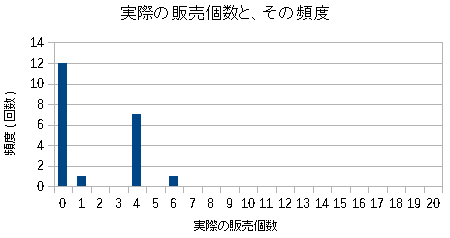 |
| ポアソン分布になっていない。 |
どうれば良いのか、悩んでしまった。 そんな折、統計学を知っている友人から ベイズ理論を使えば良いかも と助言してくれた。 だが、私は・・・ ベイズ理論がわからへん!! だった。
根本的に間違えていた私の手法
出荷数を求めるため、統計を使ってみたものの 何か釈然としない上、うまくいっていない。 そんな折、大事件が起こった。 2014年4月の 消費税増税 だった。 2014年3月は増税前の買いだめのため、注文が殺到したため 2014年4月以降は、一気に売上がなくなった。 この時・・・ この時期のデータは使い物にならへん!! と思った。 この時は、時間が経てば、出荷が安定するだろうと考えた。 そしてデータを取り直せば良いと安易に考えた。
出荷数に真値はない
だが、しばらくして当たり前の事に気づいた。 私が行った統計処理には大きな誤りがあったのだ。 そもそも・・・ 出荷数の平均も推移している という事に気づいた。
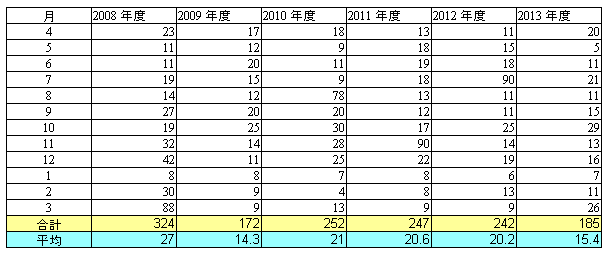
| 商品Eの年別・売上数と月の平均出荷数 |
|---|
 |
|
年によって売上合計数が大きく異なる。 1週間の平均出荷数を求めても、その値も年によってバラバラだ。 果たして、年によって出荷量合計や平均が変動するのに あたかも出荷数の真値があるように扱って 出荷数のバラツキ(標準偏差)を求める事に意味があるとは思えなくなった。 |
つまり・・・ 物理などの測定値の場合、真値があるので 統計的手法を使って真値を探ることができる しかし、出荷数量の場合、季節だけでなく、競合他社の価格差や 新製品、廉価版の代替品などの登場によって 出荷数量は左右されてしまう ので、そもそも出荷数の真値は存在しない。 そのため・・・ 真値があるという前提の統計処理は無意味 だったのだ。
相関関係
上層部は、仕入担当者に 商品出荷の季節変動を見出すように と言っていた。 だが、それも困難である事が、今回の統計で見えてきた。相関関係の求め方
「システム奮闘記:その104」(無線LANの基礎 無線LAN入門と導入事例)に書いたのだが 相関関係の求め方の復習をする。 もちろん、内容は「統計学の基礎のキ 分散と相関係数編」(石村貞夫、石村光資郎:東京図書)の丸写し。 相関関係、よくあるのが身長と体重の相関関係だ。 背が高い人は体重が重いという関係は成り立つのか 以下の表を作成してみた。
| 身長と体重 | ||
|---|---|---|
| 名前 | 身長(cm) | 体重(Kg) |
| A | 170 | 60 |
| B | 180 | 90 |
| C | 160 | 65 |
| D | 165 | 70 |
| E | 175 | 75 |
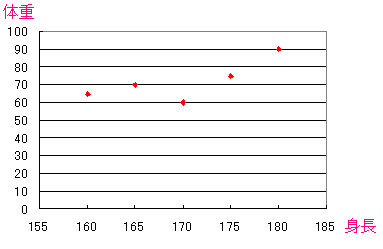
これを分布図で表すと以下のようになる。
| 5人の身長と体重の分布図 |
|---|
 |
上の分布図に、点の間を通る線を引いてみる。
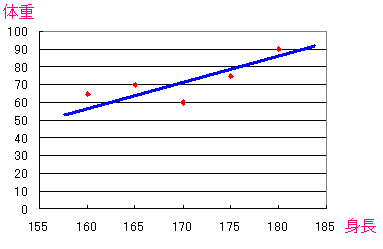
| 身長と体重の分布図 |
|---|
 |
|
線を引くと、身長と体重の間には法則性があるようだ。 相関性があるようだ。 |
視覚的みると、相関関係がありそうな分布図と 相関関係がなさそうな分布図が
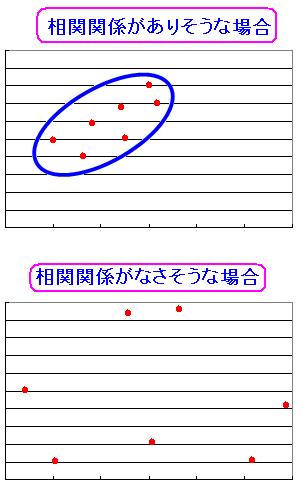
| 相関関係の有無について |
|---|
 |
|
1つの集団にまとまっているのが相関性がありそうに見える。 バラバラなのが、相関性がなさそうに見える。 |
視覚的に相関関係を見る事ができるが、本は、それだけで終わっていない。 どれくらいの相関性があるのか、数値化してみる方法が書いていた。
| 身長と体重をわけて考える |
|---|
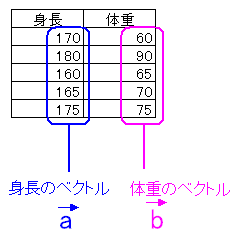 |
|
身長と体重の組み合わせではなく、身長と体重を別個に考える。 ここでは5個、成分があるので、5次元ベクトルとして考える。 |
そしてベクトルの形にして、まとめてみる。
| 身長・体重の値をベクトルでまとめる |
|---|
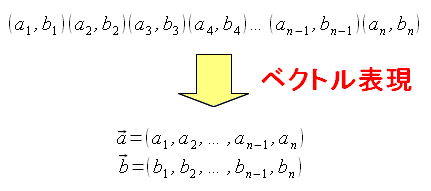 |
|
身長の、それぞれの成分を(a1,a2,a3,…,an)にし 体重の、それぞれの成分を(b1,b2,b3,…,bn)にする |
そして2つのベクトルの内積を考える。
| 2つのベクトルの内積を考える |
|---|
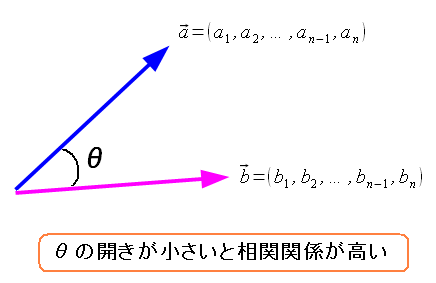 |
| ベクトルの内積とは、2つのベクトルの間の角度の大きさだ。 |
ベクトルを使う理由なのだが・・・ もし、相関関係があれば どっちも似たような方向性を持つ cosΘの値が大きければ相関関係がある という事だ。 そこで統計とベクトルの内積を組み合わせた以下の式が 相関関係を求める式になる。
| 相関関係を求める式 |
|---|
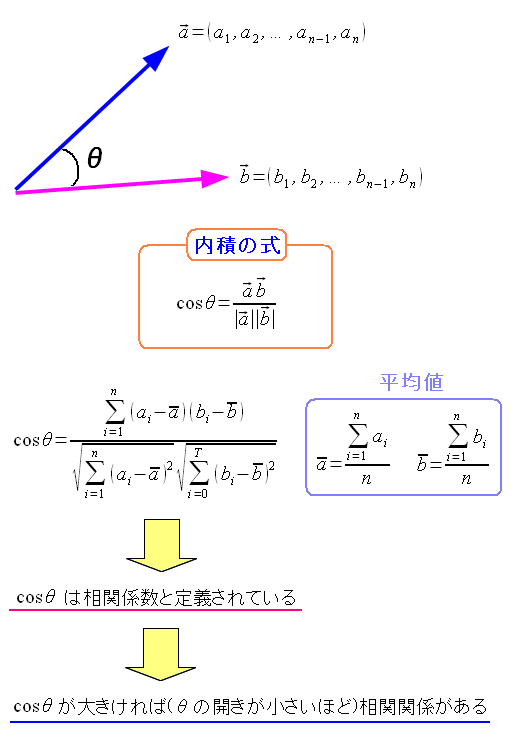 |
|
ベクトルと統計の相性の良さを感じるのだが ここでは踏み込んだ話は書かない。 踏み込めるだけの知識がないからだ。 |
相関関係の求め方がわかった所で、実際に商品Eを使って 出荷数に季節変動があるかどうか確かめる事にした。 もし、季節変動があれば、各年度ごとの月別出荷数量に 相関関係があると考えられるからだ。
| 商品Eの年度別・月別の出荷数量 |
|---|
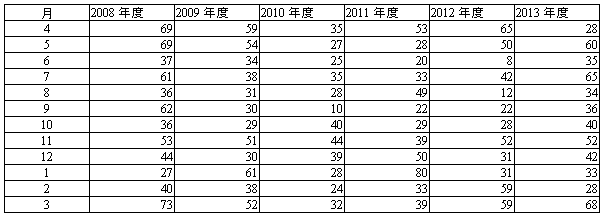 |
| 数字だけ見ると、傾向は見えてこない。 |
そこでグラフ化してみる。
| 商品Eの年度別・月別の出荷数量(グラフ) |
|---|
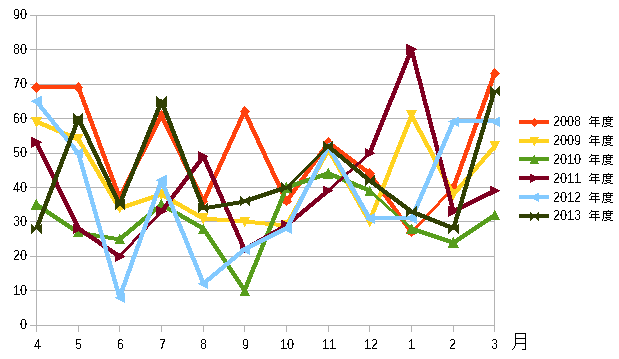 |
| 見た感じ、季節変動がなさそうに思える。 |
より見やすくするため、2008年度、2011年度、2012年度の出荷数を拾い上げて それぞれの相関係数を求めてみる事にした。
| 商品Eの2008、2011、2012年度・月別の出荷数量(グラフ) |
|---|
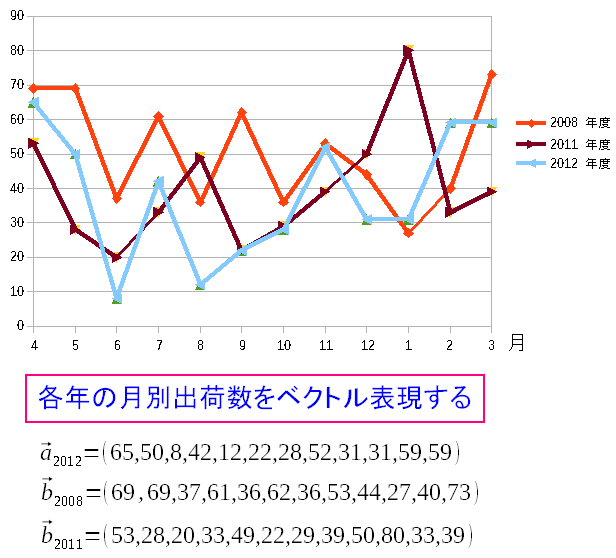 |
|
まずは2008年度、2011年度、2012年度の月別出荷数を ベクトルとして表現してみた。 |
そして相関係数を求めてみた。
| 相関係数を求めてみた |
|---|
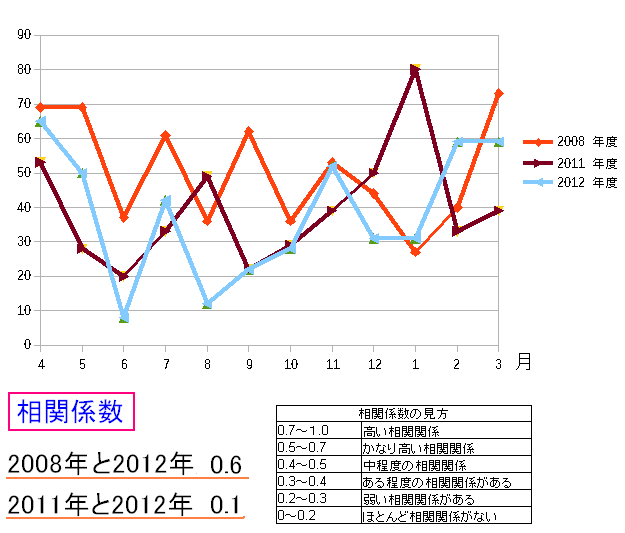 |
|
2012年度のベクトルを軸に、2008年度と2012年度。 2011年度と2012年度の相関係数を求めてみた。 すると2008年度と2012年度では強い相関関係があるものの 2011年度と2012年度では相関関係は、ほとんどない値が出た。 |
ここで課題が出た。 どこ年度を軸にするかで 相関係数が変わってくる だった。
周期性について
商品Fを見ると、なんだか周期性がありそうに思えた。
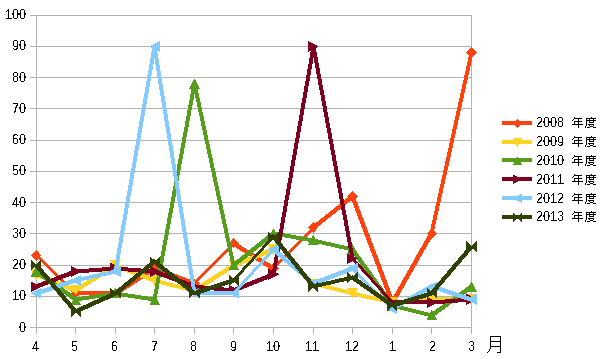
| 商品Fの月別の出荷数量 |
|---|
 |
|
ところどころに高い山がある。 周期性があるように思えた。 |
だが、周期性を見出そうとしたら、離散フーリエ変換を使う必要がある。 エクセルでできるらしいので、挑戦してみたものの・・・ うまいこと、できへん!! だった。 離散フーリエ変換については「システム奮闘記:その104」(無線LANの基礎 無線LAN入門と導入事例)をご覧ください。 その後、エクセルを使って離散フーリエ変換した物の・・・ 周期性は見つけられへんかった!! 数学を使えば、直観・感覚というものが、ただの当てずっぽである事を 実感できる例だった。
数学の勉強を開始
2015年から1年以上かけて電磁気学を勉強しなおした際 ベクトルの話がわかっていなかったのが発覚した。 そこで2016年11月、確率・統計とは全く別で、線形代数の勉強をしなおす事にした。 20年以上前に習った線形代数。相当、忘れているだろうと思った。
| スタバで線形代数の勉強中 |
|---|
 |
|
この本では線形代数の表記が「線形」ではなく「線型」になっている。 本来、「線型」が正しいようだ。 |
だが、勉強を開始すると、学生時代、線形代数は習ったはずなのに・・・ 全然、わかってへんかった!! だった。 20年以上前に習った事でも、意外と記憶の片隅にあったりする。 そして、当時、計算方法を丸暗記で誤魔化していた事が発覚した。 数学が全く理解していないと思った私。 そこで書店へ向かう。これだと思った本を発見。 必要なのは「集合」 (大蔵 陽一) だった。
| 数学の勉強方法の方向性がわかる本 |
|---|
 |
|
集合・命題などが、わかりやすく説明している。 大学で習う数学の内容や、それを学ぶのに必要な知識が わかりやすく書いていた。 |
この時・・・ 確率・統計を学ぶには相当な数学の知識が必要 だというのが、初めてわかった。 2017年3月末、今度は微分積分の勉強をしなおす事にした。 書店で何の本が良いか探していると、小平邦彦の本を発見。 この時・・・ 直感でこれだと思った だった。
| スタバで微分積分の勉強 |
|---|
 |
|
小平邦彦の「解析入門I」と「解析入門II」だ。 高校の数学がわかっていたら、読める構成になっている。 |
確かに高校の数学の知識があれば読める構成になっているのだが ε-δ論法で悶絶 だった。 数学科の学生向けの本だ。 大学にもよるが、東大などの難関大学をのぞけば、物理・工学系では 厳密な数学は教えない。もちろん、私は、難関大学なんぞ行っていないので 厳密な数学は初体験 だった。 2017年8月。今度は「集合と位相」(内田伏一)を読む。 集合・位相は、数学基本3本柱(微分積分、線形代数、集合)の1つだからだ。 神戸大学の数学科のカリキュラムでは、集合は1回生で教える内容だ。 位相は2回生で習うという。
| スタバで集合と位相の勉強 |
|---|
 |
|
集合の話で濃度が出てきた。 濃度という概念を初めて知った。 |
もちろん学生時代に習った事がないだけに 強烈に難しい。恐ろしい内容 なのだ。 だが、同時に、高校で習う三角関数で、実数論の凄い話が出ている事を 集合の話を勉強して初めて知った。 関数 y = tan(x)は 開区間(-1,1)の実数の個数と、開区間(-∞,∞)の実数の個数が同じ を表している関数だったのだ。
| 関数 y = tan(x) は実数の不思議さを表す関数 |
|---|
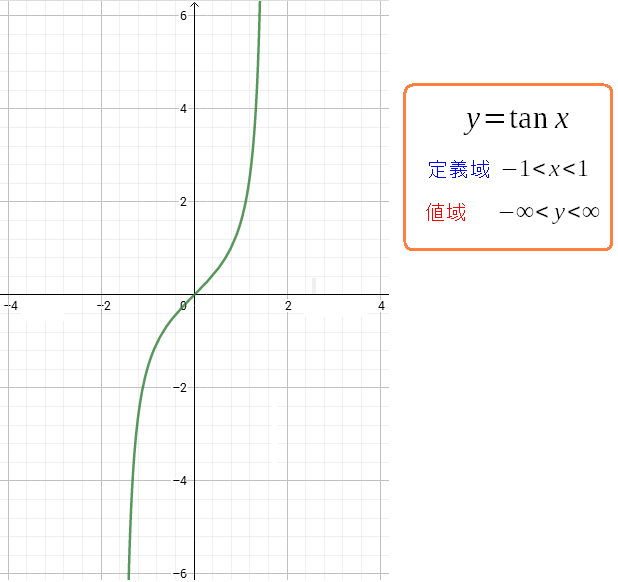 |
|
y = tan(x)の関数は、開区間(-1,1)の実数と 開区間(-∞,∞)の実数が1対1の対応関係であるのを示している。 つまり開区間(-1,1)の実数と、開区間(-∞,∞)の実数の個数が同じなのだ。 実数論では「個数」の事を「濃度」と表現している。 そのため数学書では「濃度」と書いているのだ。 |
高校1年で習ってから28年経って、その凄さを初めて知ったのだった。
2017年10月の状況 「集合と位相」(内田伏一)を読み進めたものの、位相の話になってから 全く先に進めなくなった。難しすぎて理解できない。 そこで、易しい本がないかと探して「集合と位相」(小森洋平:日本評論社)を読むことにした。
| スタバで集合と位相の勉強(2017年10月現在) |
|---|
 |
| 論理・命題が最初にあり、復習になっている。 |
何が何でも位相を理解しなければならない。 もし、ここで息切れしていたら先には進めない。 その上、まともに確率・統計を勉強しようと思ったら 微分積分、線形代数、集合・位相だけでなく ルベーグ積分も必要 なのだ。 統計学は厄介な分野だ。本当に統計学を理解しようと思うなら 微分積分、線形代数、ルベーグ積分、集合論の知識を習得しないと 確率論、数理統計学は理解できない。 だが、そういう知識がなくても、公式丸暗記、当てはめ方式でデータ処理をしても、 ある程度、実務的に使えるため、巷では統計学入門の本で溢れている。 感覚的に物事を掴むのが得意な人は、統計学の入門書を読んで、的確に分析をしたりしている。 でも、感覚的に物事を掴むのが苦手な人(私)は、とんちんかんな使い方をして、 誤った分析をする危険性が高い。 それを回避するためには、大真面目に統計学を学ばねばならないが、 非常に長くて困難な道のりが待っている。 感想。彼を知り、己を知る。そして撃沈した気分になる。 感覚的に物事をつかめる人は、うらやましい!!